一种螺线管线圈磁场快速计算方法与流程

本发明涉及电磁场数值计算，具体涉及一种螺线管线圈磁场快速计算方法。
背景技术：
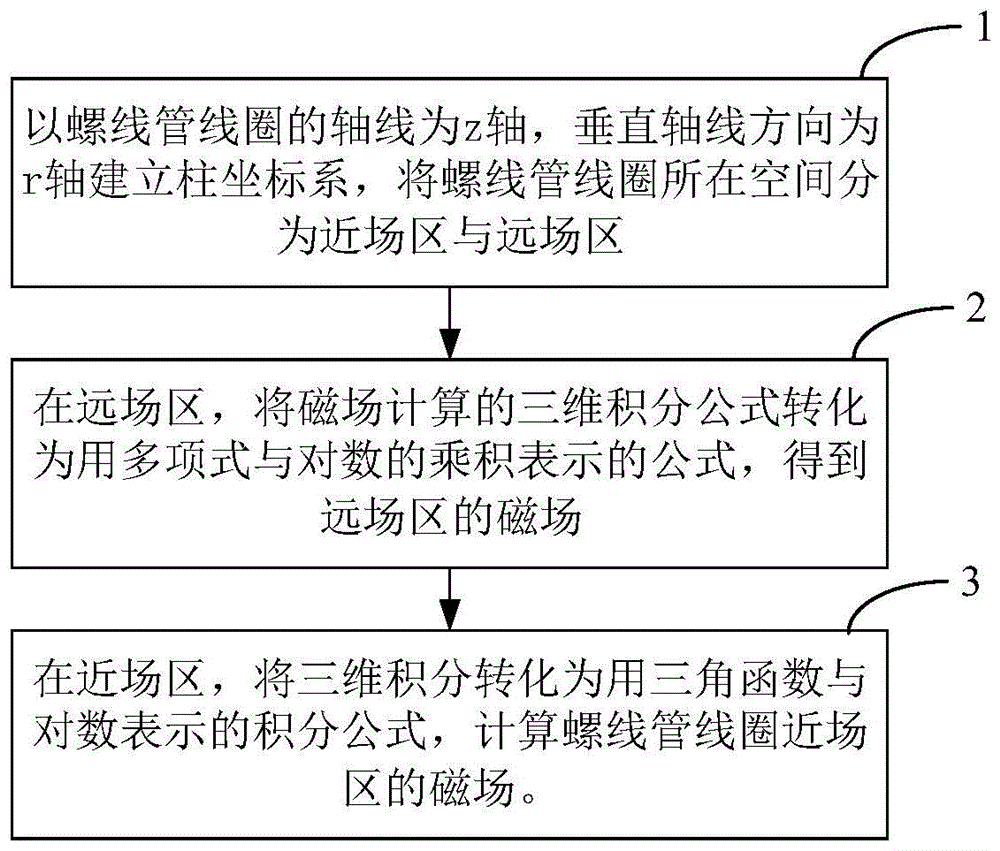
：在工程中的很多问题都需要计算螺线管产生的磁场。例如，超导磁共振系统中，超导磁体内部产生磁场的部件就是由多个螺线管线圈串联构成；此外，还有变压器等设备也是有螺线管线圈构成。这类设备的特点是，线圈里面的导线圈数多，导线长。因此如果直接采用比奥-撒伐尔定律进行磁场计算是一件非常耗时的工作。在磁共振系统中，要求的磁场均匀度在百万分之几量级。因此，磁场计算不但要求高效率，而且需要高精度。这为线圈的磁场分析以及线圈设计工作带来极大的挑战。因此，有必要提出高效的螺线管线圈磁场计算方法。技术实现要素：发明目的：本发明的目的是给出一种螺线管线圈快速计算方法，在保证磁场计算精度的前提下提高计算效率。技术方案：一种螺线管线圈快速计算方法，包括以下步骤：以螺线管线圈的轴线为z轴，垂直轴线方向为r轴建立柱坐标系，将螺线管线圈所在空间分为近场区与远场区；对于远场区，利用远场区磁场计算公式计算得到远场区磁场，所述远场区磁场计算公式是将磁场计算的三维积分公式转化为用多项式与对数的乘积表示的公式；对于近场区，利用近场区磁场计算公式计算得到近场区磁场，所述近场区磁场计算公式是将三维积分转化为用三角函数与对数表示的积分公式。进一步地，远场区磁场计算方法如下：在螺线管线圈内沿r方向取p1个采样点，沿z方向取p2个采样点，每个采样点处的坐标为(ρ′i,z'j)，则螺线管线圈在空间坐标(ρ,z)处产生的磁场如下：其中，(bρ,bz)表示螺线管线圈在场点产生的ρ,z方向的磁场分量，ωρi、ωzj为对应的权重系数，j表示线圈内的电流密度，s是螺线管线圈的横截面面积，两个拟合函数pz(ρ′i,z'j,ρ,z)，pρ(ρ′i,z'j,ρ,z)的表达式如下：当ρ＝0时：pρ(ρ′i,z'j,ρ,z)＝0当ρ≠0时：其中，μ0为真空中的磁导率，i为圆环载流，π表示圆周率，an,bn,cn,dn为多项式拟合系数，k为多项式阶次，参数k的定义如下：eρ、ez的定义如下：近场区磁场计算公式如下：其中f(r,z,ρ,z)、g(r,z,ρ,z)是与螺线管线圈尺寸有关的函数，计算公式如下：式中，n为预先设置的正整数，对应角度方向的采样点个数，vi为权重系数，为柱坐标内的角度坐标，与νi(1≤i≤n)的值为区间[0,π]内的n点高斯积分的积分点与权重系数；其它各项参数定义如下：γi＝z-zχi＝r-αi有益效果：本发明将磁场分为近场区与远场区，将磁场计算的三维积分转化为二维积分与一维积分公式，然后采用数值算法计算，从而极大的加速了磁场计算效率，并且保证了计算精度。与直接计算三维积分相比，采用本发明的方法计算效率可提升十余倍甚至上百倍。附图说明图1为根据本发明的螺线管线圈磁场快速计算方法流程图；图2为根据本发明的线圈截面区分近场区远场区示意图；图3根据一实施例的超导磁体线圈在空间的分布示意图；图4为根据一实施例的磁场均匀度为5ppm的等值线示意图。具体实施方式下面结合附图对本发明的技术方案作进一步说明。螺线管线圈由多层多匝圆环线圈串联组成。螺线管线圈产生的磁场可以采用比奥-撒伐尔定律计算，分别计算每个圆环产生的磁场然后进行累加得到总的磁场值，也可以将螺线管线圈看作横截面为矩形、电流均匀分布的线圈结构，通过推导可以将磁场写作一个二维积分的形式。无论采用哪一种方法，计算圆环产生的磁场都是一个耗时的工作。本发明给出一种更简便的磁场计算方法。参照图1，一种螺线管线圈磁场的快速计算方法，具体包括以下步骤：步骤1，以螺线管线圈的轴线为z轴，垂直轴线方向为r轴建立柱坐标系，将螺线管线圈所在空间分为近场区与远场区。一般而言，在线圈内以及附近区域为近场区，除此之外为远场区。简言之，线圈截面为一个矩形，近场区就是包含线圈截面且比线圈截面大一点的矩形，如图2所示。具体地，本发明中线圈远场区采用如下公式定义：ρ≥r2+ε∪ρ≤r1-ε∪z≥z2+ε∪z≤z1-ε(1)(ρ,z)表示场点在柱坐标系下的坐标，r1、r2分别表示螺线管线圈内外半径，z1、z2分别表示螺线管线圈两端的轴向坐标，其中z2为沿着z轴正方向的一端坐标，z1为沿着相反方向的一端坐标，ε是预先设置的一个变量。在本发明实施例中，ε＝1e-7。步骤2，在远场区，将磁场计算的三维积分公式转化为用多项式与对数的乘积表示的公式，得到远场区的磁场。在螺线管线圈内沿r方向取p1个采样点，沿z方向取p2个采样点，每个采样点处的坐标为(ρ′i,z'j)，对角度方向积分用拟合公式代替，剩下一个关于ρ,z方向的二维积分，则螺线管线圈在空间坐标(ρ,z)处产生的磁场如下：式中，(bρ,bz)表示螺线管线圈在场点产生的ρ,z方向的磁场分量，ωρi、ωzj为对应的权重系数，j表示线圈内的电流密度，s是螺线管线圈的横截面面积，两个拟合函数pz(ρ′i,z'j,ρ,z)，pρ(ρ′i,z'j,ρ,z)的表达式如下：当ρ＝0时：pρ(ρ′i,z'j,ρ,z)＝0(5)当ρ≠0时：这里的μ0为真空中的磁导率，i为圆环载流，π表示圆周率，an,bn,cn,dn为多项式拟合系数，参数k的定义如下：eρ、ez的定义如下：进一步地，k＝4时，拟合公式精度能达到10-8。，an,bn,cn,dn的值为：a0＝1.0,b0＝0a1＝0.44325141463,b1＝0.24998368310a2＝0.06260601220,b2＝0.09200180037a3＝0.04757383546,b3＝0.04069697526a4＝0.01736506451,b4＝0.00526449639c0＝1.38629436112,d0＝0.5c1＝0.09666344259,d1＝0.12498593597c2＝0.03590092383,d2＝0.06880248576c3＝0.03742563713,d3＝0.03328355346c4＝0.01451196212,d4＝0.00441787012本发明中使用了采样点的值乘以一个权重系数ω来代替积分，采样点就是高斯积分点，也可用梯形积分等数值积分。进一步地，ρ′i与ωρi为[r1,r2]内p1点高斯积分的积分点与权重系数，z'j与ωzj为[z1,z2]内p2点高斯积分的积分点与权重系数。步骤3，在近场区，将三维积分转化为用三角函数与对数表示的积分公式，计算螺线管线圈近场区的磁场。近场区磁场计算公式如下：其中f(r,z,ρ,z)、g(r,z,ρ,z)是与螺线管线圈尺寸有关的函数，计算公式如下：式中，n为一个预先给定的正整数，对应角度方向的采样点个数，n的取值为n≥20，vi为权重系数，为第i个采样点的角度坐标，与νi(1≤i≤n)的值为区间[0,π]内的n点高斯积分的积分点与权重系数，函数输入参数r,z为正实数，r的取值为r1或r2，z的取值为z1或z2。式13-14是对螺线管线圈的三维磁场积分公式进行化简得到的函数。螺线管线圈的三维磁场积分公式可以根据比奥-撒伐尔定律求得，在王秋良的《高磁场超导磁体科学》中有介绍，这里不再赘述。其它各项参数定义如下：以上描述了螺线管线圈磁场的快速计算方法的具体实施步骤，应当理解，所述的步骤序号并不表示在具体计算时必须遵照上述给出的步骤顺序来执行。在本发明中之所以采用两种算法计算磁场，是因为采用步骤2的算法计算螺线管线圈内部的磁场时会出现较大的误差，甚至会出现奇异点。远场区公式不能计算近场区的场。采用步骤3的算法计算螺线管线圈内部的磁场可以很好的避免这个问题。同时近场区公式也能计算远场区的场，只是效率可能会比较低。在具体应用中，两个公式分别用在不同的区域，简言之线圈外的磁场用远场区公式计算，线圈内的场用近场区公式计算。为了验证本发明所提方法的性能和效果，下面给出对比实验。已知某一超导磁体线圈结构如图3所示。该线圈包含5个螺线管线圈。图4是该超导磁体线圈在空间产生的磁场均匀度为5ppm的等值线分布图。可以看出，在直径为45cm的球内，该线圈的均匀度在5ppm左右。分别采用两种算法计算该磁体线圈产生的磁场。一种是对该线圈内包含的每个圆环进行计算然后累加，每个圆环产生的磁场采用分段高斯积分法计算，计算精度为10-9。另一种方法是采用本发明中的方法进行计算。采用第一种方法的计算时间约为126秒钟，采用本发明中的方法所需时间约为2秒钟。可以看出，本发明方法的计算效率相比现有技术具有极大的提升。除了线圈中心的均匀度，另一个关注的指标为线圈内的最大磁场。如果采用远场区磁场计算公式，则在线圈内k取值可能会出现0值导致计算结果不准确，采用近场区公式则没有这个问题。采用本发明中的近场区公式计算的线圈内的最大磁场如表1所示。表1线圈内的最大磁场值线圈编号最大磁场13.11956722.53127931.94711442.53127953.119567无论绘制图4中的等值线还是计算表1中的最大磁场值都需要计算大量采样点处的磁场值。在本次数值实验中，远场区磁场计算速度大约是近场区磁场计算速度的3.0倍，因此远场区公式具有更高的效率。通过上述实验数据可以看出本方法计算简便快速、精度高，能为线圈的磁场分析以及线圈设计工作提供有力帮助。当前第1页12