一种内窥镜图像序列中轮廓稠密特征点描述和匹配的方法与流程

[0001]
本发明涉及图像处理领域，具体涉及一种能够针对内窥镜图像序列中软组织表面轮廓实现鲁棒、精准的轮廓形状提取、稠密特征点描述、及轮廓形状匹配的方法。


背景技术：

[0002]
ar/mr手术导航系统取得了巨大的成功。然而，由于一些技术上的困难，它们在消化内镜和腹腔镜检查中很少被应用。首先，软组织表面光滑，纹理稀疏，表面轮廓相似度很高。现有的特征提取方法大多无法获得软组织表面的稠密特征描述，这将给单眼视觉的二维/三维重建带来明显的误差。因此，ar/mr手术导航系统在软组织二维/三维重建与术前三维模型之间难以获得准确的非刚性配准。其次，软组织在导航过程中经常发生各种变形，尤其是消化器官。它会严重影响基于特征点提取和匹配的软组织表面跟踪。因此，现有的方法大多难以解决可变形目标表面的精确鲁棒跟踪问题。作为ar/mr手术导航的关键步骤，软组织表面轮廓的致密特征提取和特征点匹配已经成为消化内镜导航系统的核心技术挑战。
[0003]
现有的ar/mr手术导航系统中，软组织表面纹理稀疏，缺乏有意义的特征点，难以对软组织表面进行跟踪。然而，软组织表面的轮廓形状特征非常重要，可以作为一种稳定的特征来改善其二维/三维重建过程。目前，二维/三维重建中常用的特征提取方法主要有：尺度不变特征变换(scale invariant feature transform，sift)、加速鲁棒特征(speeded up robust features，surf)、快速定向旋转简(oriented fast and rotated brief，orb)、harris角、方向梯度直方图(histogram of oriented gridients，hog)等。轮廓形状提取方法主要有以下几种：(1)经典的边缘提取方法，如robert算子，sobel算子、prewitt算子、laplace算子、canny算子；(2)基于学习的轮廓形状提取方法。目标跟踪/匹配方法主要有：(1)经典方法跟踪方法，如lucas-kanade光流跟踪，kcf、dcf；(2)基于深度学习的目标跟踪方法。虽然现有的方法在很多场景中已经取得了很大成功，但现有的目标跟踪方法大多都是针对目标的将目标与背景区分开或使用边界框来预测目标在一帧中的位置。它可以只找到目标的全局位置，很难实现鲁邦跟踪和特征匹配。


技术实现要素：

[0004]
本发明要解决的技术问题是：克服现有轮廓检测过程中对噪声、高光敏感的问题，提供一种能够针对内窥镜图像序列中软组织表面轮廓实现鲁棒、精准的轮廓形状提取、稠密特征点描述、及轮廓形状匹配的方法，该方法满足了不同场景的要求，应用范围广。
[0005]
本发明采用的技术方案为：一种内窥镜图像序列中轮廓稠密特征点描述和匹配的方法，包括以下步骤：
[0006]
第一步：基于双边滤波器增强自适应rpca分解所获得的低秩图像的边缘轮廓，减少图像中的干扰，然后基于梯度算子提取边缘轮廓信息，并通过形态学运算获得目标的轮廓形状；
[0007]
第二步：通过提取轮廓形状上顶点的多尺度几何特征描述子：包括:轮廓上相关三
个顶点与轮廓几何中心点构成的两个三角形面积(triangular signed area，tsa)、轮廓上当前顶点与相邻两个顶点构成三角形的几何中心点与当前顶点的距离(contour centroid distance，ccd)、计算多边形边长的比例(ratio of the edge lengths of polygons，rep)、多边形的角度大小(polygon multiple angles，pma)构造轮廓形状的稠密特征描述子，使其对轮廓形状的尺度、大小、旋转变化鲁棒；
[0008]
第三步：利用fft对轮廓形状的稠密特征描述子降维，通过计算两个轮廓的特征矩阵间的距离大小来衡量不同轮廓间的相似程度，根据目标轮廓形状，在内窥镜图像序列中对目标轮廓形状进行匹配、跟踪，在每一帧中计算获得目标轮廓形状；
[0009]
第四步：根据第三步的跟踪结果，基于时空连续性原理，运用目标轮廓形状的关键张量空间对目标轮廓的跟踪、匹配结果进行优化。
[0010]
进一步的，所述步骤1中，针对低秩图像利用sobel梯度算子提取目标稳定的边缘轮廓信息，首先基于自适应rpca获得图像的低秩结果，低秩矩阵分解公式为：
[0011][0012][0013]
其中，o(l,s,y)代表目标函数，||
·
||1表示1-范数，||
·
||
*
代表核范数，l代表低秩矩阵，s代表稀疏矩阵，m代表迭代计算过程中的中间结果，h代表检测获得的高光图像，μ代表经验常数，代表m-l-s矩阵的forbenius范数，＜y,m-l-s＞代表迭代计算过程中的残差结果，代表矩阵s的1-范数，其中m，n分别代表矩阵的行数和列数，||s-h||2表示稀疏结果与检测到的高光图像之间的相似性度量，λ
l
代表低秩控制参数，λs代表稀疏控制参数，y为基于残差m-l-s的拉格朗日乘子矩阵，ζ代表残差控制条件，η表示迭代终止条件；低秩图像能够消除内窥镜图像中高光带来的影响，将图像中包含高光信息、扰动信息、噪声信息全部分解到稀疏结果矩阵中，将图像中稳定部分、主成分分解到低秩结果矩阵中。
[0014]
进一步的，所述步骤1中，基于两个高斯滤波器将低秩图像中不稳定的抖动边缘信息消除，同时保留稳定的边缘轮廓信息，其计算公式如下：
[0015][0016][0017]
其中，bf代表保边滤波函数，l代表低秩矩阵，其中，bf代表保边滤波函数，l代表低秩矩阵，lp和lq分别表示像素p和q的强度，代表空间高斯权重算子，代表像素范围域高斯权重算子，w
p
代表归一化算子，i，j代表图像中像素的坐标位置，k，l代表与i，j坐标点临近的坐标点，σ代表高斯函数的参数，b
l
代表保边滤波后的结果图像。
[0018]
进一步的，所述步骤1中，获得低秩图像的双边滤波结果，针对滤波后图像，对其进行梯度运算，找到图像中梯度信息：
[0019][0020][0021]
其中，g
x
，g
y
分别代表x和y方向梯度，分别代表x方向和y方向导数，b
l
代表保边滤波后的结果图像，m
′
代表梯度的幅值大小，m，n分别代表图像的长、宽，θ代表梯度的方向角度大小，i，j代表图像像素坐标位置。
[0022]
进一步的，所述步骤1中，计算结束后，获得图像的轮廓集合：c＝{e1，e2，e3，...，e
t
}，t代表图像中包含的轮廓数量，e
i
表示一个小的轮廓；针对细小的边缘轮廓线进行形态学闭运算，并对细微的边缘轮廓线进行空洞填充，最后，基于4-邻域的连通域准则最终获得目标的最外围轮廓顶点；其计算过程如下所示：
[0023][0024]
其中，
·
代表形态学闭运算，代表形态学扩张运算，一代表形态学侵蚀运算，s代表7
×
7的结构元素，c代表图像中包含的轮廓形状的集合。
[0025]
进一步的，所述步骤2中，软组织表面轮廓形状的多尺度稠密几何特征提取具体为：
[0026]
(1)根据前一个轮廓自适应调整当前轮廓的大小、尺度，使得两个轮廓的大小、尺度保持一致，针对前一个轮廓的最外围包围轮廓线c
p
＝{p1，p2，p3，
…
，p
r
}，c
p
代表前一个轮廓，p
r
代表轮廓上的坐标顶点，r代表轮廓上顶点的个数，及当前轮廓的包围轮廓线c
c
＝{p1，p2，p3，
…
，p
s
}，c
c
代表当前轮廓，p
s
代表轮廓上的坐标顶点，s代表当前轮廓上顶点的个数；首先，求出轮廓的最小包围矩形的坐标：
[0027]
box(cp)＝[xp，yp，wp，hp]，
[0028]
box(cc)＝[xc，yc，wc，hc]，
[0029]
β＝sqrt((size(box(cp)))/(size(box(cc)))，
[0030]
其中，c
p
代表前一个轮廓形状，c
c
代表当前轮廓形状，box代表最小矩形函数，xp，yp，wp，hp分别代表前一个轮廓的起始坐标x，y位置信息和长度、宽度，xc，yc，wc，hc分别代表当前轮廓的起始坐标x，y位置信息和长度、宽度，β代表前一个轮廓的最小外接矩形与当前轮廓的最小外接矩形面积大小的倍数，size代表获得图像大小的函数，/代表除运算；
[0031]
然后根据β的数值范围对当前轮廓进行自适应处理，其计算公式如下所示：
[0032][0033]
其中，β代表前一个轮廓的最小外接矩形与当前轮廓的最小外接矩形面积大小的倍数，wc，hc分别代表当前轮廓的长宽大小，ki代表自适应调整前轮廓中包含的顶点个数，
kn代表自适应调整后轮廓中包含的顶点个数，nc代表自适应处理后轮廓的最小包围矩形，自适应处理后重新计算获得新的轮廓顶点h＝{p1，p2，p3，
…
，pm’}，m’代表轮廓中包含的顶点坐标的个数；
[0034]
(2)针对轮廓顶点提取多尺度稠密几何特征描述子：tsa、ccd、rep、pma；
[0035]
多尺度tsa：tsa的几何特征包括：r和q，其中r和q分别表示由轮廓上的相关的三个顶点和轮廓的几何中心点这四个点构成的两个三角形的面积大小，针对轮廓h＝{p1，p2，p3，
…
，p
m’}，首先对轮廓上的顶点进行采样处理，然后计算两个三角形r：p
i
op
ω
和q：p
i
op
φ
的面积大小，其中φ＝i-h(k
′
)，ω＝i+h(k
′
)，h(k
′
)＝2k
′-1
，1≤k
′
≤t
s
，o代表轮廓的几何中心坐标，其计算过程如下所述：
[0036][0037][0038]
s
′
＝s(h)＝{p1，p2，p3，...，p
m
′
}，
[0039]
t
s
＝log2(size(s
′
))，
[0040][0041][0042][0043]
其中，τ代表采样的基数，一般取64，n
′
代表计算获得的需要针对顶点进行采样后的顶点个数，δd代表对轮廓顶点进行采样时的间隔大小，//代表求整运算，s表示对轮廓点进行采样的函数，x
c
，y
c
分别代表轮廓顶点的中心坐标，分别代表两个三角形的面积计算结果的集合，t
s
代表根据轮廓坐标顶点数量计算其特征提取的尺度大小，size代表计算轮廓的坐标顶点数量的函数，p
i
表示轮廓形状上的一个顶点，o代表轮廓的中心坐标点，size代表获得图像大小的函数，x
i
，y
i
分别代表轮廓顶点的坐标，r
1i
(p
i
)代表轮廓顶点p
i
在尺度为1时与相邻顶点构成的三角形p
i
op
ω
的面积大小，q
1i
(p
i
)代表轮廓顶点p
i
在尺度为1时与相邻顶点构成的三角形p
i
op
φ
的面积大小；
[0044]
r和q分别代表两个三角形的面积：δp
i
op
ω
和δp
i
op
φ
，ω代表沿着当前顶点顺时针方向的下一个轮廓顶点，φ代表沿着当前顶点逆时针方向的下一个轮廓顶点；其中φ＝i-h(k
′
)，ω＝i+h(k
′
)，h(k
′
)＝2k
′-1
，1≤k
′
≤t
s
，代表三角形：p
i
op
ω
的面积计算函数，该三角形面积的计算公式如下：
[0045][0046]
然后，计算获得每个顶点的多尺度tsa特征描述符：
[0047]
多尺度ccd：通过计算当前顶点与三角形p
φ
p
i
p
ω
的几何中心顶点之间的距离，计算
过程如下：
[0048][0049][0050]
其中，d(p
i
)代表计算两个顶点之间的欧式距离，x
i
和y
i
代表顶点p
i
的坐标，x
c
和y
c
代表三角形p
φ
p
i
p
ω
的几何中心坐标，d(p
1i
)代表尺度为1时三角形几何中心坐标与轮廓顶点坐标间的欧式距离，t
s
代表尺度大小，最终计算轮廓顶点的多尺度ccd特征描述符：mccd；多尺度rep特征：通过计算多边形p
φ
p
i
p
ω
o边长长度的比值大小获得；边长比值对轮廓的尺度和旋转变化鲁棒，其计算公式如下所述：
[0051][0052][0053][0054][0055][0056]
其中，φ代表i-h(k)，ω代表i-h(k)，h(k)＝2
k-1
，κ，λ，μ，η，ρ分别代表多边形p
φ
p
i
p
ω
o的边长大小，x
c
，y
c
分别代表轮廓的几何中心坐标，o代表轮廓的几何中心坐标，最后计算获得多尺度为每个点代表特征描述符：
[0057][0058]
多尺度pma特征：通过计算多边形p
φ
p
i
p
ω
o在多个尺度下的角度大小来获得轮廓顶点的多尺度角度特征，计算公式如下所述：
[0059]
α＝arccos(p
i
p
φ
·
p
i
p
ω
/|p
i
p
φ
|
×
|p
i
p
ω
|)
×
180/π，
[0060]
β＝arccos(p
φ
p
ω
·
op
ω
/|p
φ
p
ω
|
×
|op
ω
|)
×
180/π，
[0061]
γ＝arccos(p
φ
o
·
p
ω
o/|p
φ
o|
×
|p
ω
o|)
×
180/π，
[0062]
δ＝arccos(p
ω
o
·
p
ω
p
φ
/|p
ω
o|
×
|p
ω
p
φ
|)
×
180/π，
[0063]
∈＝arccos(p
φ
p
i
·
p
φ
p
ω
/|p
i
p
φ
|
×
|p
φ
p
ω
|)
×
180/π，
[0064]
其中，α，β，γ，δ，∈分别代表四边形p
φ
p
i
p
ω
o的四个内角角度大小，p
i
p
φ
，p
i
p
ω
，p
φ
p
ω
，op
ω
，p
φ
o，p
ω
o分别代表四边形p
φ
p
i
p
ω
o的四条边和两条对角线；然后，计算获得每个顶点的多尺度pma特征描述符：
[0065][0066]
最后，提取轮廓顶点的13个多尺度几何特征，将轮廓顶点p
i
的多尺度特征描述子表示为：m
i
＝{mtsa(p
i
)，mccd(p
i
)，mrep(p
i
)，mpma(p
i
)}，1＜i＜m
′
，m
′
代表轮廓上顶点的个数。
[0067]
进一步的，所述步骤3中，特征描述子矩阵降维：
[0068]
根据上述轮廓特征描述矩阵，首先对每一列向量进行归一化，归一化公式如下所示：
[0069][0070]
其中m
i
代表轮廓坐标顶点，r
′
代表矩阵的列数，p
i
的多尺度特征描述矩阵，m矩阵中的值被规范化为-1到1；然后利用fft对特征描述矩阵降维处理；然后分别得到前一轮廓和当前轮廓的稠密特征描述子矩阵：
[0071]
f
pf
＝|{m
p1
，m，...，m
pl
}
t
|，
[0072]
f
cf
＝|{m
c1
，m
c2
，...，m
cl
}
t
|，
[0073]
其中m
p1
代表前一个轮廓顶点1的多尺度几何特征描述子，t代表矩阵转置，m
c1
代表当前轮廓顶点1的多尺度几何特征描述子，f
pf
表示前一帧的轮廓形状的特征提取结果，f
cf
表示当前帧的轮廓形状的特征提取结果，l代表特征描述矩阵降维后的维数大小；然后，通过计算两个特征向量之间的欧氏距离，来测量不同轮廓之间的相似程度，结果越大，代表两个轮廓之间的差异越大，反之亦然，相似性度量计算公式为：
[0074][0075]
其中d
pf
表示前一帧的轮廓形状的特征提取结果，d
cf
表示当前帧的轮廓形状的特征提取结果，l代表矩阵的行数，r
′
代表矩阵的列数。
[0076]
进一步的，所述步骤4中，优化跟踪、匹配结果具体包括：根据步骤三的结果，针对轮廓形状的全局匹配结果，基于目标关键张量空间中的目标轮廓形状匹配结果进行优化；对于内窥镜下的图像序列f：
[0077]
f＝{i1，i2，i3...i
s’}，
[0078]
每一帧图像i
i
包含若干个轮廓形状：s’为图像序列的数量；
[0079]
i
i
＝{c1，c2，c3...c
k’}，c
k’为图像中包含的所有轮廓的数量。
[0080]
对于每一个目标轮廓形状：c
t
，计算每一帧i
i
中对应的目标轮廓结果，然后构造关键张量空间t
c
，其中t
c
表示目标轮廓c
t
的关键张量空间：t
c
＝{c
t1
，c
t2
，c
t3
...c
tq’}，q’代表张量空间中目标的模板数量。如果全局匹配结果显示目标变形或遮挡大于阈值，将更新目标c
t
的关键张量空间t
c
，最后，将优化内镜图像序列中目标轮廓形状的匹配关系。
[0081]
本发明的原理在于：
[0082]
(1)现有的轮廓检测方法对于噪声敏感的问题。基于低秩图像能够对噪声、高光鲁棒，并通过双边滤波来增强边缘信息，本发明提出了一种边缘信息增强、提取新方法。
[0083]
(2)本发明提出一种新的轮廓形状多尺度稠密特征提取方法，该方法通过提取轮廓顶点的多尺度几何特征来描述轮廓形状的变化，这些特征对于旋转、尺度、形变鲁棒。
[0084]
(3)本发明通过fft提取的特征矩阵降维，通过计算降维矩阵的欧式距离度量不同轮廓之间的相似程度。
[0085]
(4)通过构造目标轮廓的关键张量空间，对内窥镜图像序列中目标轮廓的匹配结果进行优化。
[0086]
本发明与现有技术相比的优点在于：
[0087]
1、本发明的方法中提出了一种新的轮廓提取方法，首先基于自适应鲁棒主成分分析来获得图像的低秩结果，并利用双边滤波来增强图像中的边缘部分，该方法克服了传统边缘检测方法对于噪声、高光敏感的问题。
[0088]
2、本发明的方法中提出了一种多尺度稠密的几何特征描述子提取方法，它提取轮廓形状的稠密特征描述，其能够对旋转、尺度、形变鲁棒。
[0089]
3、本发明的方法通过关键张量来优化目标轮廓的匹配结果，能自适应场景的变化，并适用于不同的微创手术场景。
附图说明
[0090]
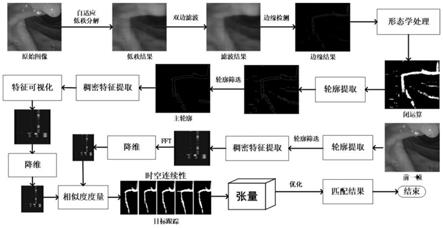
图1为本发明方法实现流程图；
[0091]
图2为本发明中图像轮廓提取流程图；
[0092]
图3为本发明中自适应rpca矩阵分解的内窥镜图像序列中高光去除方法总体流程图；
[0093]
图4为本发明中迭代优化rpca矩阵分解过程的流程图；
[0094]
图5为原始内窥镜图像序列与本发明高光去除后的效果示意图；(a)为原始内窥镜图像序列；(b)为sobel算子轮廓检测结果；(c)为laplacian算子轮廓检测结果；(d)canny算子轮廓检测结果；(e)为dog算子轮廓检测结果；(f)为本发明的轮廓检测结果。
具体实施方式
[0095]
下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整的描述，显然，所描述的实施例仅为本发明的一部分实施例，而不是全部的实施例，基于本发明中的实施例，本领域的普通技术人员在不付出创造性劳动的前提下所获得的所有其他实施例，都属于本发明的保护范围。
[0096]
如图1-4所示，本发明能够针对内窥镜图像序列中软组织表面轮廓实现鲁棒、精准的轮廓形状提取、稠密特征点描述、及轮廓形状匹配的方法，实现步骤如下：
[0097]
1、目标轮廓形状提取。参见图2，本发明提出了一种在低秩空间中利用梯度算子提取目标稳定的边缘轮廓信息，该方法首先基于自适应rpca分解获得原始内窥镜图像的低秩结果，参见图3，该低秩矩阵分解公式为：针对低秩图像利用sobel梯度算子提取目标稳定的边缘轮廓信息，首先基于本发明的自适应rpca获得图像的低秩结果，该低秩矩阵分解公式为：
[0098][0099][0100]
其中，o(l，s，y)代表目标函数，||
·
||1表示1-范数，||
·
||
*
代表核范数，l代表低秩矩阵，s代表稀疏矩阵，m代表迭代计算过程中的中间结果，h代表检测获得的高光图像，μ代表经验常数，代表m-l-s矩阵的forbenius范数，<y，m-l-s>代表迭代计算过程
中的残差结果，代表矩阵s的1-范数，其中m，n分别代表矩阵的行数和列数，||s-h||2表示稀疏结果与检测到的高光图像之间的相似性度量，λ1代表低秩控制参数，λs代表稀疏控制参数，y为基于残差m-l-s的拉格朗日乘子矩阵，ζ代表残差控制条件，η表示迭代终止条件。低秩图像能够消除内窥镜图像中高光带来的影响，将图像中包含高光信息、扰动信息、噪声信息全部分解到稀疏结果矩阵中，将图像中稳定部分、主成分分解到低秩结果矩阵中。低秩结果能够消除内窥镜图像中高光带来的影响，将图像中包含高光信息、扰动信息、噪声信息全部分解到稀疏结果矩阵中，将图像中稳定部分、主要成分分解到低秩结果矩阵中。
[0101]
此时低秩结果中保留了图像中最稳定的组成部分，其图像中并没有包含任何具有显著变化的特征变化，而且低秩图像大多呈现一种模糊效果。但是，消化类器官软组织具有非常突出的轮廓变化，为此，本发明基于两个高斯滤波器将低秩图像中不稳定的抖动边缘信息消除的同时保留稳定的边缘轮廓信息。之后利用保边滤波器对低秩图像处理，消除图像中扰动信息，获得稳定的边缘轮廓信息。针对滤波后图像，基于梯度算子实现边缘梯度信息提取。其计算公式如下：
[0102][0103][0104]
其中，bf代表保边滤波函数，其中，bf代表保边滤波函数，其中，bf代表保边滤波函数，lp和lq分别表示像素p和q的强度，代表空间高斯权重算子，代表像素范围域高斯权重算子，w
p
代表归一化算子，i，j代表图像中像素的坐标位置，k，l代表i，j坐标点临近的坐标点，σ代表高斯函数的参数，b
l
代表保边滤波后的结果图像。针对bl图像，本发明对其进行梯度运算，找到图像中梯度信息，
[0105][0106]
其中，g
x
，g
y
分别代表方向梯度，b
l
代表保边滤波后的结果图像，m代表梯度的幅值大小，m，n代表图像的大小，θ代表梯度的方向。
[0107]
计算结束后，获得图像的轮廓集合：c＝{e1，e2，e3，...，e
t
}，然后，基于形态学运算，对细小的边缘轮廓线形态学闭运算，并对细微的边缘轮廓线进行空洞填充，最后，基于4-邻域的连通域准则最终获得目标的包围轮廓顶点。其计算过程为：
[0108][0109]
其中t代表轮廓的个数，整幅图像中包含了t个边缘轮廓提取结果，式中，e
i
表示小轮廓，
·
表示形态学闭合运算，表示形态学扩张运算，表示形态学侵蚀作用，s表示结构元素。
[0110]
根据前一个轮廓自适应调整当前轮廓的大小、尺度，使得两个轮廓的大小、尺度保
持一致，针对前一个轮廓的最外围包围轮廓线c
p
＝{p1，p2，p3，
…
，p
r
}，c
p
代表前一个轮廓，p
r
代表轮廓上的坐标顶点，r代表轮廓上顶点的个数，及当前轮廓的包围轮廓线c
c
＝{p1，p2，p3，
…
，p
s
}，c
c
代表当前轮廓，p
s
代表轮廓上的坐标顶点，s代表当前轮廓上顶点的个数；首先，求出轮廓的最小包围矩形的坐标：
[0111]
box(cp)＝[xp，yp，wp，hp]，
[0112]
box(cc)＝[xc，yc，wc，hc]，
[0113]
β＝sqrt((size(box(cp)))/(size(box(cc)))，
[0114]
其中，c
p
代表前一个轮廓形状，c
c
代表当前轮廓形状，box代表最小矩形函数，xp，yp，wp，hp分别代表前一个轮廓的起始坐标x、y位置信息和长度、宽度，xc，yc，wc，hc分别代表当前轮廓的起始坐标x、y位置信息和长度、宽度，β代表前一个轮廓的最小外接矩形与当前轮廓的最小外接矩形面积大小的倍数，size代表获得图像大小的函数，/代表除运算；
[0115]
2、然后根据β的数值范围对当前轮廓进行自适应处理，其计算公式如下所示：
[0116][0117]
其中，β代表前一个轮廓的最小外接矩形与当前轮廓的最小外接矩形面积大小的倍数，wc，hc分别代表当前轮廓的长宽大小，k
i
代表自适应调整前轮廓中包含的顶点个数，k
n
代表自适应调整后轮廓中包含的顶点个数，n
c
代表自适应处理后轮廓的最小包围矩形的大小，自适应处理后重新计算获得新的轮廓顶点h＝{p1，p2，p3，
…
，p
m
}，m代表轮廓中包含的顶点坐标的个数；
[0118]
针对轮廓顶点提取多尺度稠密几何特征描述子：tsa、ccd、rep、pma。
[0119]
多尺度tsa：tsa的几何特征包括：r和q，其中r和q分别表示由轮廓上的三个顶点和轮廓的几何中心点这四个点构成的两个三角形的面积大小，针对轮廓h＝{p1，p2，p3，
…
，p
m
}，首先对轮廓上的顶点进行采样处理，然后本发明计算两个三角形r：p
i
op
ω
和q：p
i
op
φ
，其中φ＝i-h(k)，ω＝i+h(k)，h(k)＝2
k-1
，1≤k≤t
s
，t
s
＝log2(size(s
′
))，o代表轮廓的几何中心坐标，计算公式，如下所示：
[0120][0121][0122]
s＝s(h)＝{p1，p2，p3，...，p
u
}，
[0123]
t
s
＝log2(size(s))，
[0124][0125]
[0126][0127]
其中，τ代表采样的基数，一般取64，n
′
代表计算获得的需要针对顶点进行采样后的顶点个数，δd代表对轮廓顶点进行采样时的间隔大小，//代表求整运算，s表示对轮廓点进行采样的函数，x
c
，y
c
分别代表轮廓顶点的中心坐标，分别代表两个三角形的面积计算结果的集合，t
s
代表根据轮廓坐标顶点数量计算其特征提取的尺度大小，size代表计算轮廓的坐标顶点数量的函数，p
i
表示轮廓形状上的一个顶点，o代表轮廓的中心坐标点，size代表获得图像大小的函数，x
i
，y
i
分别代表轮廓顶点的坐标，r
1i
(p
i
)代表轮廓顶点p
i
在尺度为1时与相邻顶点构成的三角形p
i
op
ω
的面积大小，q
1i
(p
i
)代表轮廓顶点p
i
在尺度为1时与相邻顶点构成的三角形p
i
op
φ
的面积大小；
[0128]
r和q分别代表两个三角形的面积：δp
i
op
ω
和δp
i
op
φ
，ω代表沿着当前顶点顺时针方向的下一个轮廓顶点，φ代表沿着当前顶点逆时针方向的下一个轮廓顶点；其中其中φ＝i+h(k)，ω＝i+h(k)，h(k)＝2
k-1
，1≤k≤t
s
，代表三角形：p
i
op
ω
的面积计算函数，该三角形面积的计算公式如下：
[0129][0130]
然后，计算获得每个顶点的多尺度tsa特征描述符：
[0131]
多尺度ccd：通过计算当前顶点与三角形p
φ
p
i
p
ω
的几何中心顶点之间的距离，计算过程如下：
[0132][0133][0134]
其中，d(pi)代表计算两个顶点之间的欧式距离，x
i
和y
i
代表顶点p
i
的坐标，x
c
和y
c
代表三角形p
φ
p
i
p
ω
的几何中心坐标，d(p
1i
)代表尺度为1时三角形几何中心坐标与轮廓顶点坐标间的欧式距离，t
s
代表尺度大小，最终计算轮廓顶点的多尺度ccd特征描述符：mccd；多尺度rep特征：通过计算多边形p
φ
p
i
p
ω
o边长长度的比值大小获得；边长比值可以对轮廓的尺度和旋转变化鲁棒，其计算公式如下所述：
[0135][0136][0137][0138][0139][0140]
其中，φ代表i-h(k)，ω代表i+h(k)，h(k)＝2
k-1
，κ，λ，μ，η，ρ分别代表多边形p
φ
p
i
p
ω
o的边长大小，x
c
，y
c
分别代表轮廓的几何中心坐标，最后计算获得多尺度为每个点代表特征描述符：
[0141][0142]
多尺度pma特征：通过计算多边形p
φ
p
i
p
ω
o在多个尺度下的角度大小来获得轮廓顶点的多尺度角度特征，计算公式如下所述：
[0143]
α＝arccos(p
i
p
φ
·
p
i
p
ω
/|p
i
p
φ
|
×
|p
i
p
ω
|)
×
180/π，
[0144]
β＝arccos(p
φ
p
ω
·
op
ω
/|p
φ
pω|
×
|op
ω
|)
×
180/π，
[0145]
γ＝arccos(p
φ
o
·
p
ω
o/|p
φ
o|
×
|p
ω
o|)
×
180/π，
[0146]
δ＝arccos(p
ω
o
·
p
ω
p
φ
/|p
ω
o|
×
|p
ω
p
φ
|)
×
180/π，
[0147]
∈＝arccos(p
φ
p
i
·
p
φ
p
ω
/|p
i
p
φ
|
×
|p
φ
p
ω
|)
×
180/π，
[0148]
其中，α，β，γ，δ，∈分别代表四边形p
φ
p
i
p
ω
o的四个内角角度大小，p
i
p
φ
，p
i
p
ω
，p
φ
p
ω
，op
ω
，p
φ
o，p
ω
o分别代表四边形p
φ
p
i
p
ω
o的四条边和两条对角线；然后，计算获得每个顶点的多尺度pma特征描述符：
[0149]
然后，本发明得到每个顶点的多尺度pma特征描述符：
[0150][0151]
最后，提取轮廓顶点的13个多尺度几何特征，将轮廓顶点p
i
的多尺度特征描述子表示为：m
i
＝{mtsa(p
i
)，mccd(p
i
)，mrep(p
i
)，mpma(p
i
)}，1＜i＜m，m代表轮廓上顶点的个数。
[0152]
3、轮廓稠密特征描述子矩阵降维。根据上述轮廓特征描述矩阵，首先对每一列向量进行归一化，归一化公式如下所示：根据上述轮廓特征描述矩阵，首先对每一列向量进行归一化，归一化公式如下所示：
[0153][0154]
其中m
i
代表轮廓坐标顶点，r
′
代表矩阵的列数，p
i
的多尺度特征描述矩阵，m矩阵中的值被规范化为-1到1；然后利用fft对特征描述矩阵降维处理；然后分别得到前一轮廓和当前轮廓的稠密特征描述子矩阵：
[0155]
f
pf
＝|{m
p1
，m，...，m
pl
}
t
|，
[0156]
f
cf
＝|{m
c1
，m
c2
，...，m
cl
}
t
|，
[0157]
其中m
p1
代表前一个轮廓顶点1的多尺度几何特征描述子，t代表矩阵转置，m
c1
代表当前轮廓顶点1的多尺度几何特征描述子，f
pf
表示前一帧的轮廓形状的特征提取结果，f
cf
表示当前帧的轮廓形状的特征提取结果，l代表特征描述矩阵降维后的维数大小；然后，通过计算两个特征向量之间的欧氏距离，来测量不同轮廓之间的相似程度，结果越大，代表两个轮廓之间的差异越大，反之亦然，相似性度量计算公式为：
[0158]
其中d
pf
表示前一帧的轮廓形状的特征提取结果，d
cf
表示当前帧的轮廓形状的特征提取结果，l代表矩阵的行数，r
′
代表矩阵的列数。
[0159]
4、优化轮廓跟踪、匹配结果。最后，针对轮廓形状的全局匹配结果，基于目标关键张量空间中的目标轮廓形状匹配结果进行优化。
[0160]
对于内窥镜下的图像序列f：f＝{i1，i2，i3...i
s’}，每一帧图像i
i
包含若干个轮廓
形状：s’为图像序列的数量；i
i
＝{c1，c2，c3...c
k’}，c
k’为图像中包含的所有轮廓的数量。
[0161]
对于每一个目标轮廓形状：c
t
，计算每一帧i
i
中对应的目标轮廓结果，然后构造关键张量空间t
c
，其中t
c
表示目标轮廓c
t
的关键张量空间：t
c
＝{c
t1
，c
t2
，c
t3
...c
tq，
}，q’代表张量空间中目标的模板数量。如果全局匹配结果显示目标变形或遮挡大于阈值，将更新目标c
t
的关键张量空间t
c
，最后，将优化内镜图像序列中目标轮廓形状的匹配关系。
[0162]
内窥镜图像中轮廓提取结束后，通过计算轮廓间的相似度大小，在内窥镜图像序列中检测目标轮廓，最终实现软组织表面轮廓提取、跟踪，其结果如图5所示。其中(a)代表原始图像；(b)代表拉普拉斯算子；(c)代表canny算子；(d)代表高斯差分算子；(e)代表本发明的结果。
[0163]
实验使用的设备为python、intel(r)i7 8700k cpu(4.8ghz，8核)和32gb ram，运行在windows 10 64位系统上。
[0164]
本发明未详细阐述的技术内容属于本领域技术人员的公知技术。
[0165]
尽管上面对本发明说明性的具体实施方式进行了描述，以便于本技术领的技术人员理解本发明，但应该清楚，本发明不限于具体实施方式的范围，对本技术领域的普通技术人员来讲，只要各种变化在所附的权利要求限定和确定的本发明的精神和范围内，这些变化是显而易见的，一切利用本发明构思的发明创造均在保护之列。