一种基于数值模拟利用回归算法预测炉膛氧气浓度的方法与流程

本发明涉及一种预测炉膛氧气浓度的方法，属于燃煤锅炉
技术领域：
。
背景技术：
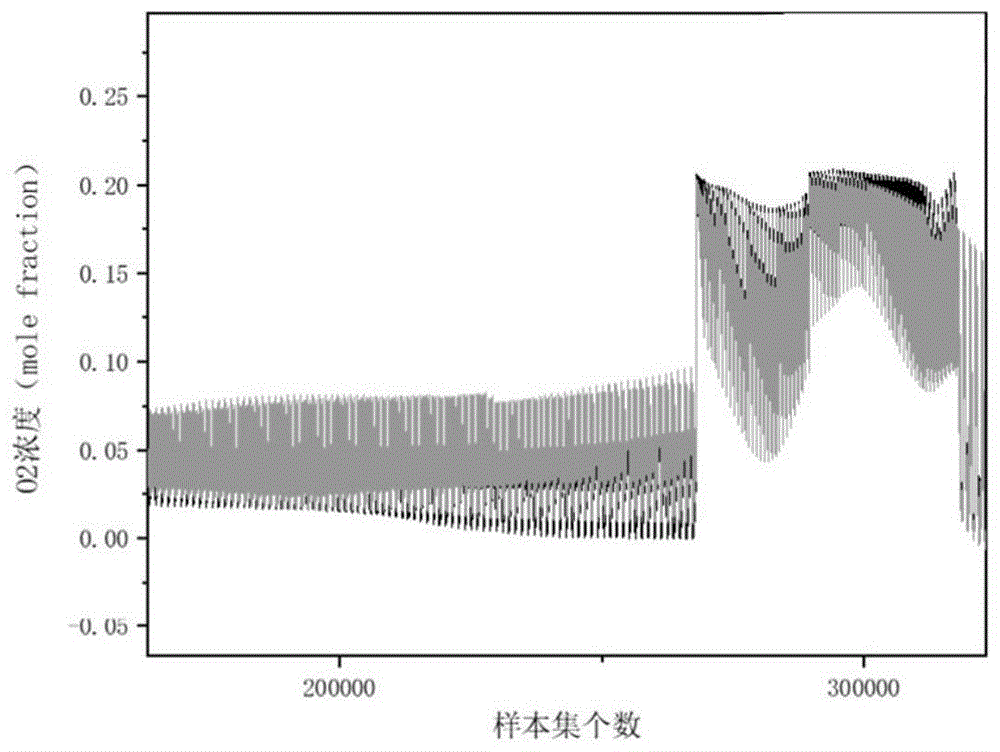
：燃煤锅炉在运动中产生含有co2，so2等的烟气，燃烧不充分时也会产生少量的co，ch4等。如果锅炉配风不当，炉膛漏风并且烟气里又含有氧，那么炉膛燃烧过程中，与入炉膛的氧充分接触达到充分燃烧，所以保持适当的过量空气，保证煤粉在炉膛的充分燃烧非常必要。但是一旦出现供给燃烧的空气量增大，会有部分o2没有被利用，作为热烟气从烟囱排放掉。这不仅增加了排烟热损失，也直接影响了锅炉运行的经济性。因此，控制锅炉燃烧中的氧含量显得尤为重要，也是衡量锅炉指标的依据之一。目前对锅炉氧浓度测量大部分停留在对烟气的氧含量测量上，导致无法准确得知炉膛内部氧含量的具体分布，无法准确对送引风量与角度进行控制。基于上述问题，亟需提出一种基于数值模拟利用回归算法预测炉膛氧气浓度的方法，以解决上述技术问题。技术实现要素：本发明提供一种基于数值模拟利用回归算法预测炉膛氧气浓度的方法，本发明研发解决的是锅炉氧浓度测量方法无法准确得知炉膛内部氧含量的具体分布的问题。在下文中给出了关于本发明的简要概述，以便提供关于本发明的某些方面的基本理解。应当理解，这个概述并不是关于本发明的穷举性概述。它并不是意图确定本发明的关键或重要部分，也不是意图限定本发明的范围。本发明的技术方案：一种基于数值模拟利用回归算法预测炉膛氧气浓度的方法，包括以下步骤：步骤一：数值模拟仿真根据锅炉运行数据与设计数据，构建炉膛内部的物理模型，选取cfd计算用煤质数据、一、二次风风温及分配方式，确定数值模拟计算边界条件；选择湍流、多相流、对流、辐射及煤粉的燃烧机理模型，利用fluent软件(计算流体动力学软件)对锅炉燃烧进行全炉膛的数值仿真，从而得到炉膛内部任意位置的氧气浓度分布数据；步骤二：数据处理经仿真模拟后输出的数据进行标准化处理，再采用数据挖掘与主成分析法进行数据集划分，参数处理，整合冗余，降低维数；经处理后得到的6个主成分；步骤三：算法预测将岭回归，随机梯度下降，回归模型(lasso)，支持向量回归(svr)集合成回归算法学习机，通过此学习机预测炉内氧量，编写程序将岭回归，随机梯度下降，lasso，svr算法集成，整合成回归算法学习机，通过此学习机预测炉膛内部氧量分布；将训练数据通过回归算法学习机训练网络，分别形成不同的网络；将验证集的输入数据分别通过这四种网络，得到预测结果；步骤四：结果应用通过比对拟合程度，均方根误差评价指标，选出结果最好的算法，为最终的预测算法，预测出指定工况下的燃烧器出口风量。优选的：所述步骤一中，确定研究对象为炉膛内氧量分布，通过ansysfluent软件(计算流体动力学软件)的export(输出)功能输出txt格式实验数据，分析与氧含量有关的锅炉运行变量，所述变量包括：锅炉内部各点坐标x,y,z，各点流体旋度和速度，co，co2，n2，o2，h2o，so2浓度，温度，压强和挥发分。优选的：所述步骤二中选取数据聚类方式对处理过的数据进行挖掘处理，数据聚类方式为k均值聚类算法。优选的：所述步骤三中将岭回归，随机梯度下降，lasso，svr集合成回归算法学习机，通过此学习机预测炉内氧量。优选的：所述步骤三中岭回归预测氧量，假定岭回归模型的损失函数为：其中j(β)为损失函数，βj为回归参数，x为特征变量，y为实际输出，λ为正则项系数，在此预测中，λ取0.1；最终对测试集输出氧浓度分布预测数据进行结果分析与评价；步骤三中随机梯度下降预测氧量，假定随机梯度下降模型的损失函数为：其中，j(β)为损失函数，βj为回归参数，α为学习率。将公式(2)代入公式(1)中，得到：不断迭代改变βj的使损失函数根据梯度下降的方向减小，直至j(β)达到最小值，随机梯度下降是随机选取其中的一个训练数据进行参数更新，以减小计算过程的复杂度，收敛速度快；输入测试集数据进行测试，对测试集输出氧浓度分布预测数据进行结果分析与评价；步骤三中lasso预测氧量，假定lasso模型的损失函数为：其中j(β)为损失函数，βj为回归参数，x为特征变量，y为实际输出，λ为正则项系数,；βj的选取，使用次梯度的方法，对第一部分rss求偏导，得到：每次选取以为进行优化并不断迭代得到最优回归系数；步骤三中svr预测氧量，支持向量回归机中损失函数如下：其中wtxi+b＝0为超平面表达式，y为实际输出，ε为惩罚系数；在此基础上，引入松弛变量来控制超出误差范围的样本的惩罚程度，对于非线性svr，需要引入核函数，通过非线性映射到高维的特征空间中，进行线性回归运算；在本预测中，degree＝3，epsilon＝0.1,松弛变量c＝1，核函数选择径向基rbf。优选的：所述步骤五中设计好要预测的工况，包括各点流体旋度和速度；co，co2，n2，o2，h2o，so2浓度，温度，压强和挥发分作为输入数据，利用最优的回归算法，预测各层燃烧器喷口风量。优选的：所述数据集通过岭回归，随机梯度下降，lasso，svr这四种回归算法后，选出误差小、准确率高的算法。优选的：所述岭回归和随机梯度下降预测和实际有部分结果有偏差，lasso和svr预测和实际结果大致重合；回归算法评价指标有拟合程度r^2，平均绝对误差mae，均方误差mse，均方根误差rmse。优选的：所述svr拟合程度高，选择svr作为最终预测算法。本发明具有以下有益效果：1.本发明基于数值模拟结果，利用fluent软件对锅炉燃烧进行全炉膛的数值仿真，从而得到炉膛内部任意位置的氧气浓度分布数据；将无法观察的炉膛内部氧气分布场，用数据进行可视化；2.本发明将岭回归，随机梯度下降，lasso，svr四种回归算法集成，选择预测效果最好的算法进行预测，比单纯用一种算法进行预测的准确率高；3.本发明基于数值模拟结果利用回归算法预测炉膛氧气浓度；数值模拟会有操作步骤多，工作量大，仿真模拟速度慢，数值分析过程耗时长、典型工况覆盖面窄等问题；而回归算法处理信息量大、计算速度快、通过简便快捷的方式处理复杂问题、能较为精准的预测未来；因此现提出一种基于数值模拟的利用回归算法预测炉膛氧气浓度的方法，提升计算效率。附图说明图1是岭回归预测结果示意图；图2是随机梯度下降预测结构示意图；图3是lasso预测结果示意图；图4是svr预测结果示意图；具体实施方式首先需要说明的是，本发明中运用到的各种计算方法如未明确说明的，均为本领域技术人员公知或熟练掌握的知识内容，例如岭回归，随机梯度下降，lasso，svr集合成回归算法，等等。因不属于本发明重点阐释内容，故不再赘述。具体实施方式一：结合图1-图4说明本实施方式，本实施方式的一种基于数值模拟利用回归算法预测炉膛氧气浓度的方法，对火电机组炉膛氧气浓度进行模拟预测，以提高锅炉燃烧效率；针对采集的离线数据，用数值模拟软件建立炉膛的物理模型，并在icem(一种专业的cae前处理软件)中对其网格进行划分及边界设定；利用ansysfluent对划分好的模型进行求解仿真，得到数据结果；利用数据处理方法处理数值模拟结果；利用回归算法学习机进行预测，最终实现炉膛内部氧量分布的预测，为实现锅炉实际运行提供理论和实践依据，包括以下步骤：步骤一：数值模拟仿真根据锅炉运行数据与设计数据，构建炉膛内部的物理模型，选取cfd计算用煤质数据、一、二次风风温及分配方式，确定数值模拟计算边界条件；选择湍流、多相流、对流、辐射及煤粉的燃烧机理模型，利用fluent软件对锅炉燃烧进行全炉膛的数值仿真，从而得到炉膛内部任意位置的氧气浓度分布数据；步骤二：数据处理经仿真模拟后输出的数据进行标准化处理，再采用数据挖掘与主成分析法进行数据集划分，参数处理，整合冗余，降低维数；经处理后得到的6个主成分，其中主成分是由仿真模拟后通过变量自动生成；步骤三：算法预测将岭回归，随机梯度下降，lasso，svr集合成回归算法学习机，通过此学习机预测炉内氧量，编写程序将岭回归，随机梯度下降，lasso，svr算法集成，整合成回归算法学习机，通过此学习机预测炉膛内部氧量分布；将训练数据通过回归算法学习机训练网络，分别形成不同的网络；将验证集的输入数据分别通过这四种网络，得到预测结果；将所有数据随机划分；整体数据的百分之七十作为训练数据，整体数据的百分之三十作为测试数据。步骤四：结果应用通过比对拟合程度，均方根误差评价指标，选出结果最好的算法，为最终的预测算法，预测出指定工况下的燃烧器出口风量。具体实施方式二：结合图1-图4说明本实施方式，本实施方式的一种基于数值模拟利用回归算法预测炉膛氧气浓度的方法，所述步骤一中，确定研究对象为炉膛内氧量分布，通过ansysfluent软件的export功能输出txt格式实验数据，分析与氧含量有关的锅炉运行变量，所述变量包括：锅炉内部各点坐标x,y,z，各点流体旋度和速度，co，co2，n2，o2，h2o，so2浓度，温度，压强和挥发分。具体实施方式三：结合图1-图4说明本实施方式，本实施方式的一种基于数值模拟利用回归算法预测炉膛氧气浓度的方法，所述步骤二中经仿真模拟后输出的数据矢量数量达到120w组，且每组数据矢量的维度和单位都不同，维度达到18维，直接使用或直接分组使用会导致数据分析不准确，预测精度不高，预测时间加长；并且如果计算机计算能力不够，会导致无法得出结果；为了提高锅炉运行过程中氧浓度的预测精度和速度，在将数据标准化处理之后，采用数据挖掘与主成分析法进行数据集划分，参数处理，整合冗余，降低维数；经处理后得到的6个主成分；无论的深度学习还是机器学习或者是回归算法，预测集中预测单点的速度要远远高于训练集中单点的预测速度；尤其是在高维数据组中，为了提高预测的速度并且提高预测的精度，更要在合理的范围内，尽量少的选取更具代表性的点的各个参数作为训练集的组成，因此本文选取数据聚类与分类的方式对上文中处理过的数据进行进一步的数据挖掘处理；综合考虑仿真实验数据的性质：将处理后得到的6个主成分作为输入数据，具有维数高，数量大，比较复杂，但输入数据具有确定性，并且数据输入顺序于网格划分的顺序一致的特点，需要很高的聚类质量特点；决定采用的数据聚类方式为k均值聚类算法(k-means)。具体实施方式四：结合图1-图4说明本实施方式，本实施方式的一种基于数值模拟利用回归算法预测炉膛氧气浓度的方法，所述步骤三中将岭回归，随机梯度下降，lasso，svr集合成回归算法学习机，通过此学习机预测炉内氧量。具体实施方式五：结合图1-图4说明本实施方式，本实施方式的一种基于数值模拟利用回归算法预测炉膛氧气浓度的方法，所述步骤二中岭回归预测氧量，假定岭回归模型的损失函数为：其中j(β)为损失函数，βj为回归参数，x为特征变量，y为实际输出，λ为正则项系数，在此预测中，λ取0.1；最终对测试集输出氧浓度分布预测数据进行结果分析与评价；步骤二中随机梯度下降预测氧量，假定随机梯度下降模型的损失函数为：其中，j(β)为损失函数，βj为回归参数，α为学习率。将公式(2)代入公式(1)中，得到：不断迭代改变βj的使损失函数根据梯度下降的方向减小，直至j(β)达到最小值，随机梯度下降是随机选取其中的一个训练数据进行参数更新，以减小计算过程的复杂度，收敛速度快；输入测试集数据进行测试，对测试集输出氧浓度分布预测数据进行结果分析与评价；步骤二中lasso预测氧量，假定lasso模型的损失函数为：其中j(β)为损失函数，βj为回归参数，x为特征变量，y为实际输出，λ为正则项系数,；βj的选取，使用次梯度的方法，对第一部分rss求偏导，得到：每次选取以为进行优化并不断迭代得到最优回归系数；步骤二中svr预测氧量，支持向量回归机中损失函数如下：其中wtxi+b＝0为超平面表达式，y为实际输出，ε为惩罚系数；在此基础上，引入松弛变量来控制超出误差范围的样本的惩罚程度，对于非线性svr，需要引入核函数，通过非线性映射到高维的特征空间中，进行线性回归运算；在本预测中，degree＝3，epsilon＝0.1,松弛变量c＝1，核函数选择径向基rbf；通过比对拟合程度，均方根误差评价指标，选出结果最好的算法，为最终的预测算法。具体实施方式六：结合图1-图4说明本实施方式，本实施方式的一种基于数值模拟利用回归算法预测炉膛氧气浓度的方法，所述步骤五中设计好要预测的工况，包括各点流体旋度和速度；co，co2，n2，o2，h2o，so2浓度，温度，压强和挥发分作为输入数据，利用最优的回归算法，预测各层燃烧器喷口风量。具体实施方式七：结合图1-图4说明本实施方式，本实施方式的一种基于数值模拟利用回归算法预测炉膛氧气浓度的方法，所述数据集通过岭回归，随机梯度下降，lasso，svr这四种回归算法后，选出误差小、准确率高的算法。具体实施方式八：结合图1-图4说明本实施方式，本实施方式的一种基于数值模拟利用回归算法预测炉膛氧气浓度的方法，在这四个图中，采用机器学习算法预测结果，深黑色为实际炉内氧气浓度。从图中可以看出，所述岭回归和随机梯度下降预测和实际有部分结果有偏差，lasso和svr预测和实际结果大致重合，最终误差以下述表格为准；回归算法评价指标有拟合程度r^2，平均绝对误差mae，均方误差mse，均方根误差rmse；其中r^2越接近于1，表示拟合程度越好，mae，mse，rmse越小表示误差越小。r^2maemsermse岭回归0.90541.54974.71812.1721随机梯度下降0.90091.59224.93792.2221lasso0.89911.61105.03182.2432svr0.93141.20503.52321.8770具体实施方式九：结合图1-图4说明本实施方式，本实施方式的一种基于数值模拟利用回归算法预测炉膛氧气浓度的方法，通过上表可以看出，所述svr拟合程度高，选择svr作为最终预测算法；基于数值模拟的利用回归算法预测炉膛内部氧量的方法，可以提升计算效率，省去大量数值模拟操作步骤及计算时间；能准确的掌握火电机组实际运行过程中氧量的分布，进一步通过调节改善锅炉炉膛内部的燃烧情况，从而维持火电机组运行的稳定性，进一步提高机组效率。需要说明的是，在以上实施例中，只要不矛盾的技术方案都能够进行排列组合，本领域技术人员能够根据排列组合的数学知识穷尽所有可能，因此本发明不再对排列组合后的技术方案进行一一说明，但应该理解为排列组合后的技术方案已经被本发明所公开。本实施方式只是对本专利的示例性说明，并不限定它的保护范围，本领域技术人员还可以对其局部进行改变，只要没有超出本专利的精神实质，都在本专利的保护范围内。当前第1页12