一种小推力航天器轨道根数长期演化的极大值估计方法与流程

1.本发明属于航天器动力学与控制领域，特别涉及一种小推力航天器轨道根数长期演化的极大值估计方法。


背景技术：

2.离子电推进等推进技术的发展带动了航天任务的设计应用的拓展。连续小推力推进以其高推进效率在航天器在轨服务、航天器轨道保持和编队交会等航天任务中有着广泛应用。
3.对于航天器长期在轨运行的任务周期，以及小推力轨迹优化等问题，通常需要进行轨道递推演化来确定航天器轨道变化范围以及确定变轨能力。如何以简便快速的方式进行小推力航天器长期轨道根数演化能够为轨迹优化及航天任务设计提供便利和参考。
4.当前小推力航天器轨道根数递推通常采用两种方式：一种是数值积分的方式，利用积分器对航天器从初始轨道进行积分，对于长轨道积分时间的情况以及轨迹优化等情况需要很大的计算量以及计算时间消耗；另一种半解析估计方式，一般是利用简化的小推力形式，只考虑单一确定方向的小推力推进，进行单一小推力方向的小推力航天器轨道根数估计，只能用于确定在此种小推力作用下，轨道根数的变化情况，无法确定小推力航天器轨道根数的变化范围边界。


技术实现要素：

5.本发明旨在解决当前小推力航天器长期轨道演化轨道根数变化极大值估计时所面临的计算量大，适用范围窄的不足之处，提出一种小推力航天器轨道根数长期演化的极大值估计方法。本发明计算消耗低，适用范围广，可提高航天器轨道根数变化量极大值估计的计算效率与适用范围。
6.本发明提出一种小推力航天器轨道根数长期演化的极大值估计方法，其特征在于，包括以下步骤：
7.1)建立航天器摄动方程：
8.对于高斯形式的拉格朗日行星运动方程，航天器轨道根数a,e,i,ω,ω,f分别代表半长轴、偏心率、轨道倾角、升交点赤经、近拱点幅角、真近点角；
9.令t＝[a
v
,a
n
,a
h
]为小推力航天器的摄动加速度，其中a
v
代表摄动加速度在密切轨道平面内沿速度方向的分量，a
n
代表摄动加速度在垂直速度方向的分量，a
h
代表摄动加速度在垂直于轨道平面的分量；
[0010]
建立航天器摄动方程表达式如下：
[0011][0012]
[0013][0014][0015][0016][0017]
其中，θ＝ω+f表示真近点角与近地点幅角之和；r,v,h,μ分别为卫星地心距、速率、角动量标量和中心天体引力常数；t表示时间变量；
[0018]
2)摄动方程转换；
[0019]
对于步骤1)得到的摄动方程式(1)-(6)，将式(1)-(5)分别除以式(6)，得到轨道根数a,e,i,ω,ω关于真近点角f的微分方程，从而得到以真近点角为自变量的高斯摄动方程式(7)-(11)，表达式如下：
[0020][0021][0022][0023][0024][0025]
3)计算航天器轨道根数长期变化量的极大值；具体步骤如下：
[0026]
3-1)设定半长轴、偏心率、轨道倾角、升交点赤经、近拱点幅角和真近点角的初值分别为a0,e0,i0,ω0,ω0,f0，设定表示使得轨道根数在一个周期变化量取极大值的最优摄动加速度，其中三个分量分别代表最优摄动加速度在密切轨道平面内沿速度方向、垂直速度方向以及垂直于轨道平面的分量；
[0027]
3-2)计算半长轴、偏心率、近拱点幅角长期变化量的极大值；具体步骤如下：
[0028]
3-2-1)设定初始周期数n＝1，则对于半长轴、偏心率、近拱点幅角存在：a
n-1
＝a0,e
n-1
＝e0,ω
n-1
＝ω0；其中，a
n-1
为第n-1个周期的半长轴，e
n-1
为第n-1个周期的偏心率，ω
n-1
为第n-1个周期的近拱点幅角；
[0029]
3-2-2)从半长轴、偏心率、近拱点幅角中任意选取一个轨道根数；
[0030]
3-2-3)计算步骤3-2-2)选取的轨道根数在第n-1个周期的变化量极大值；方法如下：
[0031]
3-2-3-1)对于半长轴；
[0032]
半长轴在第n-1个周期的变化量极大值为：
[0033][0034]
其中c
a
表示半长轴在第n-1个周期变化量极大值计算中的积分型常数；
[0035]
3-2-3-2)对于偏心率；
[0036]
使得偏心率在第n-1个周期变化率最大的最优摄动加速度在密切轨道平面内垂直速度方向分量和沿速度方向的分量分别为：
[0037][0038]
其中，||t||表示加速度矢量的模；a
n-1
,b
n-1
为用于简化加速度表示形式所引入的中间量；
[0039]
将代入式(8)，得到偏心率在第n-1个周期的变化量极大值为：
[0040][0041]
3-2-3-3)对于近拱点幅角；
[0042]
使得近拱点幅角在第n-1个周期变化率最大的最优摄动加速度的三个分量分别为：
[0043][0044]
其中，a
ω,n-1
,b
ω,n-1
,c
ω,n-1
为中间量，计算表达式分别如下：
[0045][0046]
将式(15)中的加速度分量代入式(11)，得到积分形式的近拱点幅角在第n-1个周期的变化量极大值为：
[0047][0048]
3-2-4)计算步骤3-2-2)选取的轨道根数在第n个周期的值为：
[0049][0050]
其中，为该轨道根数在第n-1个周期的变化量的极大值，x
n-1
为该轨道根数在第n-1个周期的值；
[0051]
3-2-5)令n＝n+1，然后重新返回步骤3-2-3)，直至n的取值到达设定的数值时，得到该轨道根数在第n-1个周期变化的极大值；
[0052]
3-3)计算轨道倾角、升交点赤经长期变化量的极大值；
[0053]
从轨道倾角和升交点赤经中任意选取一个轨道根数，计算该轨道根数在第n个周期的变化量极大值，方法如下：
[0054]
3-3-1)对于轨道倾角：
[0055]
使得轨道倾角一个周期变化量取得极大值的最优摄动加速度在密切轨道平面内垂直速度方向分量为：
[0056][0057]
将式(18)的结果代入式(9)里积分，得到轨道倾角在一个周期的变化量极大值为：
[0058][0059]
其中h,g是积分常数；
[0060]
则在设定的第n个周期时，轨道倾角变化极大值i
n
为：
[0061][0062]
3-3-2)对于升交点赤经：
[0063]
使得升交点赤经一个周期变化量取得极大值的最优摄动加速度在密切轨道平面内垂直速度方向分量为：
[0064][0065]
将式(21)的结果代入式(10)里积分，得到升交点赤经在一个周期的变化量极大值为：
[0066][0067]
其中c
ω
,h',g'是积分常数，
[0068]
则在设定第n个周期时，升交点赤经变化极大值ω
n
表示为：
[0069][0070]
将式(20)代入式(23)中积分，得到在第n个周期时，升交点赤经变化的极大值为：
[0071][0072]
本发明的特点及有益效果在于：
[0073]
1.本发明基于微分代数原理，利用轨道动力学特性，分析推导出小推力航天器轨道根数关于轨道周期的长期演化变化量极大值估计方法，能够快速计算出航天器轨道根数变化量极大值。相对于数值递推计算方式和单小推力方向的轨道根数变化估计方法，本发明方法属于一种半解析方式，具有计算效率高，适用范围广等优点。
[0074]
2.本发明中，对于部分轨道根数的长期演化，轨道根数变化量估计采用迭代算法，能够快速计算出相应的轨道根数变化量极大值，相比于数值积分算法能节省大量计算量。另外本方法可以针对航天器轨道周期量级上的轨道根数变化量估计，能够针对短期或者长期的轨道根数变化估计预报。
[0075]
3.在航天器动力学与控制领域，本发明可以应用于小推力轨迹优化、航天器轨道根数变化预报、航天任务可行性分析以及轨道长期演化分析。能够适用于不同类型的轨道情况，对不同轨道根数情况均能较好地进行估计，与数值准确方法相比，具有估计精度高，计算效率高等优点。
附图说明
[0076]
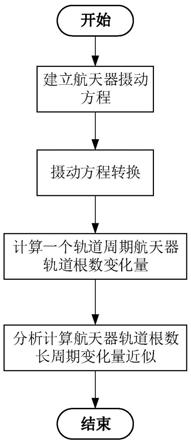
图1为本发明方法的整体流程图；
[0077]
图2为本发明实施例中半长轴变化量极大值曲线示意图；
[0078]
图3为本发明实施例中偏心率变化量极大值曲线示意图；
[0079]
图4为本发明实施例中近拱点幅角变化量极大值曲线示意图；
[0080]
图5为本发明实施例中轨道倾角变化量极大值曲线示意图；
[0081]
图6为本发明实施例中升交点赤经化量极大值曲线示意图。
具体实施方式
[0082]
本发明提出一种小推力航天器轨道根数长期演化的极大值估计方法，下面结合附图和具体实施例进一步详细说明如下。
[0083]
本发明提出一种小推力航天器轨道根数长期演化的极大值估计方法，整体流程如图1所示，包括以下步骤：
[0084]
1)建立航天器摄动方程：
[0085]
对于高斯形式的拉格朗日行星运动方程，航天器轨道根数a,e,i,ω,ω,f分别代表半长轴、偏心率、轨道倾角、升交点赤经、近拱点幅角、真近点角。令t＝[a
v
,a
n
,a
h
]为小推力航天器的摄动加速度，其中三个分量分别代表摄动加速度在密切轨道平面内沿速度方向、垂直速度方向以及垂直于轨道平面的分量。
[0086]
建立航天器摄动方程表达式如下：
[0087][0088][0089][0090][0091][0092][0093]
其中，θ＝ω+f表示真近点角与近地点幅角之和。r,v,h,μ分别为卫星地心距、速率、角动量标量和中心天体引力常数。t表示时间变量。
[0094]
2)摄动方程转换；
[0095]
对于步骤1)得到的高斯型摄动方程式(1)-(6)，摄动加速度对真近点角的改变量为相对小量，仅考虑二体情况下真近点角的变化，用前五个轨道根数的微分方程式(1)—(5)分别除以第六个方程式(6)，可以得到前五个轨道根数a,e,i,ω,ω关于真近点角f的微分方程，从而得到以真近点角为自变量的高斯摄动方程式(7)-(11)，表达式如下：
[0096][0097][0098][0099][0100][0101]
3)计算航天器轨道根数长期变化量的极大值；具体步骤如下：
[0102]
3-1)设定任意满足开普勒椭圆轨道的轨道根数初值并分别记作a0,e0,i0,ω0,ω0,f0。同时设定用带上标
*
的加速度表示使得轨道根数在一个周期变化量取极大值的最优加速度，其中三个分量分别代表最优摄动加速度在密切轨道平面内沿速度方向、垂直速度方向以及垂直于轨道平面的分量。
[0103]
3-2)计算半长轴、偏心率、近拱点幅角长期变化量的极大值；具体步骤如下：
[0104]
3-2-1)设定初始周期数n＝1，则对于半长轴、偏心率、近拱点幅角存在：a
n-1
＝a0,
e
n-1
＝e0,ω
n-1
＝ω0；
[0105]
3-2-2)从半长轴、偏心率、近拱点幅角中任意选取一个轨道根数；
[0106]
3-2-3)计算步骤3-2-2)选取的轨道根数在第n-1个周期的变化量极大值；方法如下：
[0107]
3-2-3-1)对于半长轴；
[0108]
对于半长轴的微分方程，在该周期仅有最优摄动加速度在密切轨道平面内沿速度方向分量的时候，半长轴变化率最大，则半长轴在第n-1个周期的变化量极大值为：
[0109][0110]
其中c
a
表示半长轴在第n-1个周期变化量极大值计算中的积分型常数。计算半长轴长期变化极大值的时候，偏心率e变化为小量，可以近似为保持初值不变。
[0111]
3-2-3-2)对于偏心率；
[0112]
利用最优性原理可以得到使得偏心率在第n-1个周期变化率最大的最优摄动加速度在密切轨道平面内垂直速度方向分量和沿速度方向的分量分别为：
[0113][0114]
其中，||t||表示加速度矢量的模。a
n-1
,b
n-1
为用于简化加速度表示形式所引入的中间量，e
n-1
为第n-1个周期的偏心率。
[0115]
将上述加速度分量代入偏心率的微分方程式(8)，合并同类项并化简之后可以得到偏心率在第n-1个周期的变化量极大值为：
[0116][0117]
3-2-3-3)对于近拱点幅角；
[0118]
利用最优性原理可以得到使得近拱点幅角在第n-1个周期变化率最大的最优摄动加速度的三个分量分别为：
[0119][0120]
其中为了简化上述加速度分量计算中所引入的中间量a
ω,n-1
,b
ω,n-1
,c
ω,n-1
可以表示为：
[0121][0122]
将式(15)中的加速度分量代入近拱点幅角的微分方程式(11)，可以得到积分形式的近拱点幅角在第n-1个周期的变化量极大值为：
[0123][0124]
3-2-4)按照下式更新轨道根数值，得到步骤3-2-2)选取的轨道根数在第n个周期的值为：
[0125][0126]
其中，为该轨道根数在第n-1个周期的变化量的极大值(为步骤3-2-3)中计算得到的结果)，x
n-1
为该轨道根数在第n-1个周期的值；
[0127]
3-2-5)令n＝n+1，然后重新返回步骤3-2-3)，直至n的取值到达设定的数值，即可得到该轨道根数在第n-1个周期变化的极大值；
[0128]
3-3)计算轨道倾角、升交点赤经长期变化量的极大值；
[0129]
对于轨道倾角和升交点赤经，在进行这两个轨道根数的长期变化量近似时，忽略轨道倾角变化量极大值中其他轨道根数的变化以及升交点赤经变化量极大值中除轨道倾角i之外其他轨道根数的变化。
[0130]
从轨道倾角和升交点赤经中任意选取一个轨道根数，计算该选取的轨道根数在第n个周期的变化量极大值，方法如下：
[0131]
3-3-1)对于轨道倾角：
[0132]
利用最优性原理得到使得轨道倾角一个周期变化量取得极大值的最优摄动加速度在密切轨道平面内垂直速度方向分量为：
[0133][0134]
将式(18)的结果代入轨道倾角的微分方程式(9)里积分可以得到轨道倾角在一个周期的变化量极大值(为常数)为：
[0135][0136]
其中h,g是积分常数；
[0137]
则在设定的第n个周期时，轨道倾角变化极大值i
n
为：
[0138]
[0139]
3-3-2)对于升交点赤经：
[0140]
利用最优性原理得到使得升交点赤经一个周期变化量取得极大值的最优摄动加速度在密切轨道平面内垂直速度方向分量为：
[0141][0142]
将式(21)的结果代入升交点赤经微分方程式(10)里积分可以得到升交点赤经在一个周期的变化量极大值为：
[0143][0144]
其中c
ω
,h',g'是积分常数，(为常数)；
[0145]
则在设定第n个周期时，升交点赤经变化极大值ω
n
可以表示为：
[0146][0147]
将轨道倾角变化的极大值方程式(20)代入上式(23)中积分，可以得到在第n个周期时，升交点赤经变化的极大值为：
[0148][0149]
至此，即可以得到上述五个轨道根数的长期演化变化量极大值估计值。
[0150]
实例验证
[0151]
本实施例中，航天器初始轨道根数及长期演化目标轨道圈数等仿真参数如下表所示：
[0152]
表1实例验证轨道根数初值设置表
[0153][0154]
设定小推力加速度大小为||t||＝10-4
m/s2。
[0155]
本实施例中步骤3)的详细步骤包括：
[0156]
3)计算航天器轨道根数长期变化量的极大值；具体步骤如下：
[0157]
3-1)设定任意满足开普勒椭圆轨道的轨道根数初值并分别记作a0,e0,i0,ω0,ω0,f0。同时设定用带上标
*
的加速度表示使得轨道根数在一个周期变化量取极大值的最优加速度。
[0158]
3-2)计算半长轴、偏心率、近拱点幅角长期变化量的极大值；具体步骤如下：
[0159]
3-2-1)设定初始周期数n＝1，对于给定的初始轨道的轨道根数有a
n-1
＝7500km,
e
n-1
＝0.001,ω
n-1
＝10；
[0160]
3-2-2)从半长轴、偏心率、近拱点幅角中任意选取一个轨道根数；
[0161]
3-2-3)计算步骤3-2-2)选取的轨道根数在第n-1个周期的变化量极大值；方法如下：
[0162]
3-2-3-1)对于半长轴；
[0163]
对于半长轴的微分方程，在仅有最优摄动加速度在密切轨道平面内沿速度方向分量的时候，半长轴变化率最大，则一个半长轴在第n-1个周期的变化量极大值为：
[0164][0165]
其中，e0＝0.001，c
a
表示半长轴在第n-1个周期变化量极大值计算中的积分型常数。
[0166]
3-2-3-2)对于偏心率；
[0167]
利用最优性原理可以得到使得偏心率在第n-1个周期变化率最大的最优摄动加速度在密切轨道平面内垂直速度方向分量和沿速度方向的分量分别为：
[0168][0169]
将上述加速度分量代入偏心率的微分方程式(8)，可以得到偏心率在第n-1个周期的变化量极大值为：
[0170][0171]
3-2-3-3)对于近拱点幅角；
[0172][0173]
其中：
[0174]
[0175]
将上述式(15)中的三个加速度分量代入近拱点幅角的微分方程式(11)，可以得到积分形式的近拱点幅角在第n-1个周期的变化量极大值为：
[0176][0177]
3-2-4)按照下式更新轨道根数值，得到步骤3-2-2)选取的轨道根数在第n个周期的值为：
[0178][0179]
其中，为该轨道根数在第n-1个周期的变化量的极大值(为步骤3-1-3)中计算得到的结果)，x
n-1
为该轨道根数在第n-1个周期的值；
[0180]
3-2-5)令n＝n+1，然后重新返回步骤3-2-3)，直至取值n＝[2500,3000,300],即可到该轨道根数在设定周期变化的极大值；
[0181]
图2、图3和图4分别为半长轴、偏心率、近拱点幅角变化极大值与数值解对比图，本发明所计算的对于不同的周期数n下的轨道根数变化曲线与精确的数值计算的轨道根数变化曲线相比两者基本保持一致，说明本实例采用的计算半长轴、偏心率、近拱点幅角变化极大值的方法能够很好的近似精确的轨道根数变化极大值，验证了本方法的正确性和有效性。
[0182]
3-3)计算轨道倾角、升交点赤经长期变化的极大值；具体方法如下：
[0183]
对于轨道倾角和升交点赤经，在进行这两个轨道根数的长期变化量近似时，忽略中其他轨道根数的变化以及中除轨道倾角i之外其他轨道根数的变化，即计算轨道倾角和升交点赤经变化的极大值时a0＝7500km,e0＝0.001,ω0＝10。
[0184]
从轨道倾角和升交点赤经中任意选取一个轨道根数，计算选取的轨道根数在第n个周期的变化量极大值；方法如下
[0185]
3-3-1)对于轨道倾角：
[0186]
利用最优性原理得到使得轨道倾角一个周期变化量取得极大值的最优摄动加速度在密切轨道平面内垂直速度方向分量为：
[0187][0188]
将式(18)的结果代入轨道倾角的微分方程式(9)里积分可以得到轨道在一个周期的变化量极大值(为常数)：
[0189][0190]
其中h,g是积分常数；
[0191]
则在设定的周期数n＝3000时，轨道倾角变化极大值i
n
为：
[0192][0193]
其中i0＝10。
[0194]
3-3-2)对于升交点赤经：
[0195]
利用最优性原理得到使得升交点赤经一个周期变化量取得极大值的最优摄动加
速度在密切轨道平面内垂直速度方向分量为：
[0196][0197]
将式(21)的结果代入升交点赤经微分方程式(10)里积分可以得到轨道在一个周期的变化量极大值：
[0198][0199]
其中c
ω
,h',g'是积分常数，(为常数)；
[0200]
则在设定的周期数n时，升交点赤经变化极大值ω
n
可以表示为：
[0201][0202]
将轨道倾角变化的极大值方程式(20)代入上式(23)中积分，可以得到在周期数为n＝3000时，升交点赤经变化的极大值为：
[0203][0204]
其中，ω0＝30，i0＝10，代入上式即可得升交点赤经在周期数为3000时变化的极大值。
[0205]
图5、图6分别为轨道倾角、升交点赤经变化的极大值对比所示，实线和虚线分别表示本发明所示方法计算的轨道根数变化极大值和精确的数值极大值解。通过图5、图6可以发现本发明方法计算的轨道倾角与升交点赤经变化的极大值与精确数值解计算结果基本一致，说明本方法在可以精确估计轨道倾角和升交点赤经变化的极大值，表明本方法的计算的正确性和有效性。
[0206]
综上所述，本实施例采用一种小推力轨道根数长期演化变化的极大值估计方法，应用于估计航天器轨道根数变化的极大值范围估计，与精确的数值仿真计算结果对比，能够精确有效地估计航天器在不同周期下的轨道根数变化的极大值。本实施例针对任意形式的航天器开普勒椭圆轨道，基于微分代数和轨道动力学特性，能够方便地应用于各种形式的轨道以及不同轨道周期下的轨道根数变化极大值估计。