一种高含硫碳酸盐岩生物礁气藏试井解释方法

1.本发明涉及一种高含硫碳酸盐岩生物礁气藏试井解释方法，属于气田勘探开发技术领域。


背景技术：

2.试井是油、气田勘探开发中重要的一个环节，主要是对油井、气井或水井进行测试，内容包括产量、压力、温度和取样等。它是一种以渗流力学理论为基础，构建、求解试井数学模型，建立试井对数曲线图版；并以钢丝、电缆等为手段，将压力计下入井底，测量压力、温度；然后根据图版反求压力、温度变化对应的油、气、水井的各种物理参数(地层压力、流动系数、污染状况、边界条件、边底水活跃程度)、生产能力，以及油、气、水层之间的连通关系等，为油、气田合理开发提供支撑的一种方法。试井主要包括测试工艺和测试解释方法，目前针对不同类型油、气藏已形成了多种试井解释方法。
3.对于高含硫碳酸盐岩生物礁气藏，目前主要采用常规的如图1所示的多层模型，或者如图2所示的双重介质模型进行试井解释，但存在以下几个问题：1.常规的多层模型将产层分为多个层考虑，并假设每个层储集空间为均质的，流体为单相流，其中层与层之间厚度、渗透率、孔隙度、流体饱和度等参数均不一样，它解释主要得出的参数为单个层流体渗透率k、层间窜流系数λ(刻画流体从低渗透层到高渗透层的流动能力)、地层系数比κ(刻画不同层之间的渗透性差异)；虽然生物礁气藏符合多层模型特征，但其礁基含底水，礁盖、礁核含高含硫气体，为多相流体，同时礁基，礁盖储集空间为非均质的(含孔隙与裂缝系统)，底水上窜、底水与气体在礁盖、礁核(非均质空间)中的流动特征，采用常规的多层模型无法刻画；2.常规的双重介质模型将产层简化两个系统考虑，一个为高导流裂缝系统，一个为低导流的基岩系统，假设流体为单相流，流体从基岩系统流到裂缝系统，然后由裂缝系统流到井筒，它主要得出的参数为弹性储能比ω(裂缝系统储存流体与整个系统储存流体量的比值)、窜流系数λ(刻画流体从溶孔到天然裂缝系统的流动能力)，针对高含硫碳酸盐岩生物礁气藏的底水反应、纵向上流体在礁基与礁核、礁核与礁盖间的窜流反应、人工酸压裂缝等特征并未考虑，导致试井解释的准确率低。试井解释准确率低将影响后期为气井提供合理配产依据、以及判断后期水体对气藏开发的影响程度。
4.针对常规的双重介质模型的缺陷，有人提出利用三重介质模型对该类气藏进行试井解释，例如：期刊为《特种油气藏》、期刊号为2020年第3期、名称为“弱底水碳酸盐岩礁相气藏压裂井试井模型研究”的期刊文章中建立了如图3所示的新的物理模型和试井解释方法，物理模型主要将礁相气藏外部看成一个整体，内部采用三重介质(基质系统孔、裂缝系统、溶洞系统)进行描述，并假设流体通过天然裂缝流向人工裂缝，再由人工裂缝流向井筒，基质孔隙和溶洞均作为天然裂缝的补给源；进而得出不同系统间弹性储能比ω、窜流系数λ。
5.然而上述文章中所建立的物理模型中并未考虑纵向上底水与气体在礁基与礁核、礁核与礁盖间的窜流特征，同时模型求解后建立的双对数曲线图版上，弱底水与强底水导
数特征均为下掉，二者没有明显区别，导致试井资料解释准确率低，进而刻画的气藏结构及弱底水识别方面特征吻合度较低，影响了对该类气藏的认识。


技术实现要素：

6.本技术的目的在于提供一种高含硫碳酸盐岩生物礁气藏试井解释方法，用以解决现有技术试井解释准确率低，导致对高含硫碳酸盐岩生物礁气藏认识偏差较大的问题。
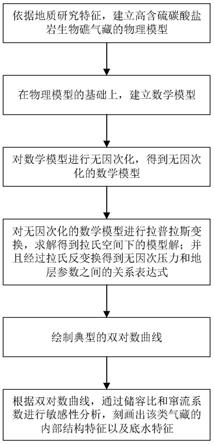
7.为实现上述目的，本技术提出了一种高含硫碳酸盐岩生物礁气藏试井解释方法的技术方案，包括以下步骤：
8.1)建立高含硫碳酸盐岩生物礁气藏的物理模型；所述物理模型包括垂向上：从上到下的礁盖、礁核、礁基，以及压裂井；压裂井的井底置于礁盖内且储层经压裂后形成双翼缝；礁盖包括天然裂缝、溶孔与天然气；礁核包括溶孔、天然气；礁基包括溶孔和底水；并且礁盖中的天然裂缝和溶孔之间存在窜流，礁盖和礁核之间存在窜流，礁核和礁基之间存在窜流；
9.2)在物理模型的基础上，利用质量守恒、达西定律和状态方程，建立该类气藏的数学模型；
10.3)将数学模型进行无因次化，得到无因次化的数学模型；
11.4)利用拉普拉斯变换求解无因次化的数学模型，得到压裂井的无因次井底压力；
12.5)根据无因次井底压力绘制无因次井底压力、压力导数与无因次时间的双对数曲线；
13.6)根据双对数曲线进行敏感性分析，刻画出该类气藏的内部结构特征和底水特征，完成该类气藏的试井解释。
14.本发明的高含硫碳酸盐岩生物礁气藏试井解释方法的技术方案的有益效果是：本发明通过研究高含硫碳酸盐岩生物礁气藏的地质特征，考虑了礁基、礁核、礁盖的结构特征，流体渗流特征以及与弱底水的影响，并且结合了气藏在开发时开发井普遍酸压造缝的工况，耦合酸压裂缝特征，进而建立了精细描述生物礁气藏内部垂向分布特征、流体渗流特征及弱底水影响的物理模型及数学模型。将建立的数学模型进行求解，绘制出双对数曲线，进而对该类气藏进行敏感性分析，完成试井解释，有效的提高了该类型气藏的认识程度。本发明充分考虑了礁基、礁核、礁盖结构特征的物性差异，并且结合酸压造缝的物性特征，能够很好的评价出酸压后储层的导流能力、污染状况以及气井供气能力，为合理布井以及工艺技术优化提供理论依据，同时本发明将弱底水很好的融入到数学模型中，使得弱底水特征在双对数曲线上能够很好的识别出来，符合该类型气藏地质静态资料的认识，可以帮助技术人员充分认识底水特性，为气井合理工作制度制定以及水处理提供指导。
15.进一步的，所述数学模型包括礁盖中天然裂缝的渗流方程、礁盖中溶孔的渗流方程、礁核的渗流方程、礁基的渗流方程以及初始条件、内边界条件、外边界条件：
16.所述礁盖中天然裂缝的渗流方程为：
[0017][0018]
礁盖中溶孔的渗流方程为：
[0019][0020]
礁核的渗流方程为：
[0021][0022]
礁基的渗流方程为：
[0023][0024]
所述初始条件为：
[0025]
p
f1
＝p
m1
＝p2＝p3＝pi；
[0026]
所述外边界条件为：
[0027][0028]
所述内边界条件为：
[0029][0030]
其中，φf为礁盖中天然裂缝的孔隙度，无量纲；kf为礁盖中天然裂缝的渗透率，μm2；c
tf
为礁盖中天然裂缝的综合压缩系数，atm-1
；p
f1
为礁盖中天然裂缝的压力，atm；φm为礁盖中溶孔的孔隙度，无量纲；km为礁盖中溶孔的渗透率，μm2；c
tm
为礁盖中溶孔的综合压缩系数，atm-1
；p
m1
为礁盖中溶孔的压力，atm；h1为礁盖的厚度，cm；(kv)
1-2
为礁盖与礁核之间界面的垂向渗透率，μm2；φa为礁核的孔隙度，无量纲；c
ta
为礁核的综合压缩系数，atm-1
；p2为礁核的压力，atm；h2为礁核的厚度，cm；(kv)
2-3
为礁核与礁基之间界面的垂向渗透率，μm2；φb为礁基的孔隙度，无量纲；c
tb
为礁基的综合压缩系数，atm-1
；p3为礁基的压力；h3为礁基的厚度，cm；μw为底水的粘度，mpa.s；μg为平均地层条件下的天然气粘度，mpa.s；pi为原始地层压力，atm；q
sc
气井地面体积流量，cm3/s；为线汇地面体积流量，bg为平均地层条件下的天然气体积系数，无量纲；t为生产时间，s；r为径向距离，cm；re为外边界半径，cm；α为形状因子，cm-2
。
[0031]
进一步的，为了提高试井解释的准确性，根据duhamel原理，结合井储系数和表皮系数求解无因次化的数学模型。
[0032]
进一步的，为了更加准确的绘制双对数曲线，所述步骤5)中根据stehfest数值反演方法绘制双对数曲线。
[0033]
进一步的，为了全面的对气藏进行敏感性分析，所述步骤6)中通过储容比和窜流系数进行敏感性分析，所述储容比包括礁盖中天然裂缝的储容系数占礁盖的储容系数的储容比、礁盖的储容系数与总储容系数的储容比、礁核的储容系数与总储容系数的储容比；窜流系数包括礁盖中天然裂缝和溶孔之间的窜流系数、礁盖与礁核之间的窜流系数、以及礁核与礁基之间的窜流系数。
附图说明
[0034]
图1是现有技术中常规的多层模型的示意图；
[0035]
图2是现有技术中常规的双重介质模型的示意图；
[0036]
图3是现有技术中三重介质模型的示意图；
[0037]
图4是本发明高含硫碳酸盐岩生物礁气藏试井解释方法的流程图；
[0038]
图5是本发明高含硫碳酸盐岩生物礁气藏物理模型的示意图；
[0039]
图6是本发明礁相弱底水气藏压裂井压力与压力导数双对数试井曲线图；
[0040]
图7是本发明不同礁盖中天然裂缝的储容系数占礁盖的储容系数的储容比下的压力与压力导数双对数试井曲线图；
[0041]
图8是本发明不同礁盖的储容系数与总储容系数的储容比下的压力与压力导数双对数试井曲线图；
[0042]
图9是本发明不同礁核的储容系数与总储容系数的储容比下的压力与压力导数双对数试井曲线图；
[0043]
图10是本发明不同礁盖中天然裂缝和溶孔之间的窜流系数下的压力与压力导数双对数试井曲线图；
[0044]
图11是本发明不同礁盖与礁核之间的窜流系数下的压力与压力导数双对数试井曲线图；
[0045]
图12是本发明不同礁核与礁基之间的窜流系数下的压力与压力导数双对数试井曲线图；
[0046]
图中：1为礁盖、2为礁核、3为礁基、4为压裂缝。
具体实施方式
[0047]
高含硫碳酸盐岩生物礁气藏试井解释方法实施例：
[0048]
近年来对高含硫碳酸盐岩生物礁气藏的地质研究发现：该类型气藏从孔隙结构来看，其储集空间以孔隙型为主，局部发育裂缝，其中：粒间溶孔、粒内溶孔、溶蚀孔洞是主要的储集空间；从沉积特征来看，其外部可作为一个整体层考虑，但其内部自下而上主要由礁基、礁核、礁盖组成，其中礁基储集底水，礁盖、礁核储集高含硫气体，存在多相流体；并且底水上窜、底水与气体在礁盖、礁核(非均质空间)中渗流，平面及纵向非均质性极强，并在压力动态测试过程中表现异常，该异常现象可能与气藏结构及底水活跃程度等特征相关联。
[0049]
为此，本发明提出的试井解释方法的主要构思在于，考虑了礁基、礁核、礁盖的结构特征，同时考虑了弱底水影响，结合气藏在开发时普遍酸压造缝的工况，耦合酸压裂缝特征，建立了精细描述高含硫碳酸盐岩生物礁气藏的物理模型及数学模型，采用拉普拉斯变换对数学模型求解以及反变换绘制出典型曲线图版，通过敏感性分析，刻画高含硫碳酸盐岩生物礁气藏的内部结构特征以及底水特征，有效提高了该类性气藏的认识程度。
[0050]
以下以某气田礁相储层为例对本发明的试井解释方法进行详细描述。具体的，试井解释方法如图4所示，包括以下步骤：
[0051]
1)根据地质特征研究，建立了高含硫碳酸盐岩生物礁气藏的物理模型。
[0052]
某气田礁相储层总体上遵循威尔逊沉积模式，所建立的物理模型如图5(图5中的向上箭头表示定产气量进行投产)所示，在垂向上划分为礁盖1、礁核2和礁基3三种微相，礁
相气藏下部与底水相连，在礁体中部打一口井(即压裂井)，只打开上部礁盖1，储层经压裂后形成双翼的压裂缝4(即双翼缝)，基本假设条件如下：
[0053]
a.礁盖1由天然裂缝和溶孔两种介质构成，礁核2由溶孔构成；
[0054]
b.礁基3由溶孔构成；
[0055]
c.天然气主要储存在礁盖1和礁核2中；
[0056]
d.底水主要存储在礁基3中，且为有限的底水(有限代表底水的量较少)；
[0057]
e.为了避免压裂缝4直接连通底水而导致气井过快水淹，只压开礁盖1的上部；
[0058]
f.气体流动满足达西定律；
[0059]
g.礁盖1的溶孔与天然裂缝间存在窜流；
[0060]
h.随着生产的进行，压力的下降，礁核2中的气体可向礁盖1窜流补给，礁基3中的底水可向礁核2进行能量补充。
[0061]
2)在步骤1)所建立的物理模型的基础上，利用质量守恒、达西定律和状态方程，建立高含硫碳酸盐岩生物礁气藏的数学模型。
[0062]
高含硫碳酸盐岩生物礁气藏一般压力较高，故气藏渗流方程可采用压力形式，因此数学模型包括礁盖1中天然裂缝的渗流方程、礁盖1中溶孔的渗流方程、礁核2的渗流方程、礁基3的渗流方程以及初始条件、内边界条件、外边界条件：
[0063]
礁盖1中天然裂缝的渗流方程为：
[0064][0065]
礁盖1中溶孔的渗流方程为：
[0066][0067]
礁核2的渗流方程为：
[0068][0069]
礁基3的渗流方程为：
[0070][0071]
初始条件为压力分布均匀，均为pi，即：p
f1
＝p
m1
＝p2＝p3＝pi；
[0072]
外边界条件为：
[0073]
内边界条件为(定产)：
[0074]
其中，φf为礁盖1中天然裂缝的孔隙度，无量纲；kf为礁盖1中天然裂缝的渗透率，μm2；c
tf
为礁盖1中天然裂缝的综合压缩系数，atm-1
；p
f1
为礁盖1中天然裂缝的压力，atm；φm为礁盖1中溶孔的孔隙度，无量纲；km为礁盖1中溶孔的渗透率，μm2；c
tm
为礁盖1中溶孔的综合压缩系数，atm-1
；p
m1
为礁盖1中溶孔的压力，atm；h1为礁盖1的厚度，cm；(kv)
1-2
为礁盖1与礁
核2之间界面的垂向渗透率，μm2；φa为礁核2的孔隙度，无量纲；c
ta
为礁核2的综合压缩系数，atm-1
；p2为礁核2的压力，atm；h2为礁核2的厚度，cm；(kv)
2-3
为礁核2与礁基3之间界面的垂向渗透率，μm2；φb为礁基3的孔隙度，无量纲；c
tb
为礁基3的综合压缩系数，atm-1
；p3为礁基3的压力；h3为礁基3的厚度，cm；μw为底水的粘度，mpa.s；μg为平均地层条件下的天然气粘度，mpa.s；pi为原始地层压力，atm；q
sc
气井地面体积流量，cm3/s；为线汇地面体积流量，bg为平均地层条件下的天然气体积系数，无量纲；t为生产时间，s；r为径向距离，cm；re为外边界半径，cm；α为形状因子，cm-2
。
[0075]
3)将步骤2)中的数学模型进行无因次化，得到无因次化的数学模型。
[0076]
本步骤的目的在于降低不同物理量纲对模型求解的干扰。具体的无因次化的过程为：
[0077]
礁盖1中天然裂缝的无因次压力p
f1d
：
[0078][0079]
礁盖1中溶孔的无因次压力p
m1d
：
[0080][0081]
礁核2的无因次压力p
2d
：
[0082][0083]
礁基3的无因次压力p
3d
：
[0084][0085]
无因次时间td：rw为井半径，cm；
[0086]
无因次井半径rd：
[0087]
由于礁盖1中天然裂缝的地层系数远远大于溶孔地层系数，因此实际计算时，溶孔地层系数可忽略，故用天然裂缝的地层系数代表礁盖1的地层系数。
[0088]
因此总地层系数＝kfh1+kmh1+kah2+kbh3，简化为总地层系数＝kfh1+kah2+kbh3；
[0089]
总储容系数＝φ
fctf
h1+φ
mctm
h1+φac
ta
h2+φbc
tb
h3；
[0090]
其中，kfh1为礁盖1中天然裂缝的地层系数；kmh1为礁盖1中溶孔的地层系数；kah2为礁核2的地层系数；kbh3为礁基3的地层系数；φ
fctf
h1为礁盖1中天然裂缝的储容系数；φ
mctm
h1为礁盖1中溶孔的储容系数；φac
ta
h2礁核2的地层系数；φbc
tb
h3为礁基3的地层系数；ka为礁核2的渗透率，μm2；kb为礁基3的渗透率，μm2。
[0091]
礁盖1的地层系数与总地层系数比χ1：
[0092]
礁核2的地层系数与总系统地层系数比χ2：
[0093]
礁盖1中天然裂缝的储容系数占礁盖1的储容系数的储容比ω
m-f
：
[0094][0095]
礁盖1的储容系数与总储容系数的储容比ω1：
[0096]
礁核2的储容系数与总储容系数的储容比ω2：
[0097]
礁基3的储容系数与总储容系数的储容比ω3：
[0098]
礁盖1中的天然裂缝和溶孔之间的窜流系数λ
m-f
：
[0099][0100]
礁盖1与礁核2之间的窜流系数λ
′
：
[0101]
礁核2与礁基3之间的窜流系数λ
″
：
[0102]
底水与天然气的粘度比μr：
[0103]
在上述无因次量的定义下，无因次化的数学模型为：
[0104]
礁盖1中天然裂缝无因次化方程：
[0105][0106]
礁盖1中溶孔无因次化方程：
[0107]
礁核2的无因次化方程：
[0108]
礁基3的无因次化方程：
[0109]
无因次初始化条件：p
f1d
＝p
m1d
＝p
2d
＝p
3d
＝0；
[0110]
无因次外边界条件：r
ed
为无因次外边界半径，无量纲；
[0111]
无因次内边界条件：无因次内边界条件：为线汇井无因次产量。
[0112]
4)利用拉普拉斯变换，将步骤3)得到的无因次化的数学模型由非线性转换为线性，并得出拉氏空间下该模型的解，进而利用拉氏反变换得出无因次压力与地层参数的关系表达式。
[0113]
具体的，将无因次化的数学模型进行laplace(拉普拉斯)变换，得：
[0114]
礁盖1中的天然裂缝变换方程：
[0115]
s为laplace变量；为经laplace变换后的礁盖1中天然裂缝的无因次压力；为经laplace变换后的礁核2的无因次压力；为经laplace变换后的礁盖1中溶孔的无因次压力。
[0116]
礁盖1中的溶孔变换方程：
[0117]
礁核2变换方程：
[0118]
礁基3变换方程：礁基3变换方程：为经laplace变换后的礁基3的无因次压力；
[0119]
外边界条件变换方程：
[0120]
内边界条件变换方程：内边界条件变换方程：为laplace变换后的无因次线汇产量；
[0121]
由礁盖1中的溶孔变换方程，得故
[0122]
由礁基3变换方程，得
[0123]
带入礁核2变换方程，得：
[0124]
故故为laplace空间中的礁盖1中天然裂缝的无因次压力；
[0125]
由外边界条件变换方程，可得：
[0126][0127]
其中，f为f＝ω
m-f
ω1s-λ
m-f
χ1(a
1-1)-λ'(a
3-1)；k1为1阶第二类变形贝塞尔函数；a为待定系数；b为待定系数；i1为1阶第一类变形贝塞尔函数。
[0128]
由内边界条件变换方程，可得：
[0129][0130]
方程
①②
组成了一个2阶线性代数方程组，可以确定2个待定系数a、b。当确定待定系数后，线汇引起的laplace变换后的礁盖1中天然裂缝的无因次压力就确定了，其表达式如下：
[0131][0132]
线汇引起的laplace变换后的礁盖1中天然裂缝的无因次压力响应仅仅代表一条线汇引起的，而压裂缝4可视为两个对称面，根据叠加原理，对线汇引起的压力响应沿着裂缝长度方向(从-xf到xf)积分，xf为压裂缝4半长(单位，cm)，即可获得压裂缝4(即对称面)引起压力响应，再经无因次化后，即可获得压裂井(即压裂缝4)的无因次压力响应。
[0133][0134]
上式中，i0为零阶第一类变形贝塞尔函数；k0为零阶第二类变形贝塞尔函数；β为积分变量；为laplace空间中的无因次压力分布，它代表压裂井在气藏中任意一点的无因次压力响应，根据坐标关系可知。根据gringarten等学者在研究其他问题时所获得的结论，当上式中rd内的参数xd取特定值0.732时，即可用之等效计算无限导流情况下的压裂井的无因次井底压力响应；当上式中rd内的参数xd取特定值0时，即可获得均匀流情况下的压裂井的无因次井底压力响应。因此，礁盖1、礁核2、礁基3、弱底水情况下的礁相气藏压裂井的无因次井底压力响应(或压力解)即获得。
[0135]
以上的计算并没有考虑表皮系数s和井储系数cd的影响。当存在表皮效应和井筒储集效应时，可以通过下式来考虑，当然这并不是必须考虑的过程。该式主要由duhamel原理结合井储系数和表皮系数的定义给出：
[0136][0137]
其中，为不考虑表皮和井储时的井底压力响应，即就是当xd取特定值0.732或0时的0时的为考虑井储和表皮效应时的礁盖1、礁核2、礁基3、弱底水情况下的礁相气藏压裂井的无因次井底压力响应(或压力解)。
[0138]
对于是否考虑表皮系数s和井储系数cd均可以的得到井底压力，进行后续步骤的试井解释，本发明对此不做限制。
[0139]
5)根据步骤4)得到的无因次井底压力解，绘制高含硫碳酸盐岩生物礁气藏的典型试井双对数曲线。
[0140]
采用stehfest数值反演方法，利用计算机可绘制礁相弱底水气藏压裂井的无因次井底压力p
wd
、压力导数p
wd
′
·
(td/cd)与无因次时间td/cd的双对数曲线，如图6所示，图6中平缓的曲线对应无因次井底压力，凹凸不平的曲线对应压力导数。对于弱底水礁相气藏的压裂气井，其典型曲线可能出现8个渗流阶段：
[0141]
①
早期纯井筒储集段。此段压力及压力导数在双对数图上呈斜率为1的直线段；
[0142]
②
井储后的过渡段，表现为一“驼峰”；
[0143]
③
地层向压裂缝4线状流阶段，导数曲线呈斜率为1/2的直线；
[0144]
④
基质溶孔流体向天然裂缝的窜流段。此阶段礁盖1中基质溶孔与天然裂缝间的压差已建立，基质溶孔向天然裂缝进行窜流，该段压力导数呈一个向下的“凹子”；
[0145]
⑤
裂缝-基岩系统(即溶孔)径向流段。此阶段基质溶孔向裂缝的窜流达到平衡，裂缝与基岩的压力同步下降，压力导数曲线又趋于0.5水平线；
[0146]
⑥
礁核2中的天然气向礁盖1补给反映段，此阶段礁核2与礁盖1中的压差已建立，礁核2中的天然气向礁盖1进行补给，该段压力导数又呈一个向下的“凹子”；
[0147]
⑦
礁基3中的底水向礁核2能量补充反映段，此阶段礁基3与礁核2中的压差已建立，礁基3中的底水向礁核2进行能量补充，该段压力导数又呈一个向下的“凹子”；
[0148]
⑧
总系统径向流段。
[0149]
6)根据双对数曲线特征，通过礁盖1中天然裂缝的储容系数占礁盖1的储容系数的储容比ω
m-f
、礁盖1的储容系数与总储容系数的储容比ω1、礁核2的储容系数与总储容系数的储容比ω2、礁盖1中的天然裂缝和基质溶孔之间的窜流系数λ
m-f
、礁盖1与礁核2之间的窜流系数λ
′
、礁核2与礁基3之间的窜流系数λ
″
等参数的敏感性分析，刻画高含硫碳酸盐岩生物礁气藏内部结构特征以及底水特征，完成试井解释。
[0150]
改变礁盖1中天然裂缝的储容系数占礁盖1的储容系数的储容比ω
m-f
，得到不同ω
m-f
下的无因次井底压力与压力导数的对比曲线，如图7所示，图7中两条平缓的曲线对应不同ω
m-f
下的无因次井底压力，区分不明显，凹凸不平的两条曲线对应不同ω
m-f
下压力导数，导数曲线更能够分辨储层特征，从图7可以得出结论：ω
m-f
越小，压力导数曲线上第一个“凹子”越宽越深。
[0151]
改变礁盖1的储容系数与总储容系数的储容比ω1，得到不同ω1下无因次井底压力与压力导数的对比曲线，如图8所示，图8中两条平缓的曲线对应不同ω1下的无因次井底压力，区分不明显，凹凸不平的两条曲线对应不同ω1下压力导数，导数曲线更能够分辨储层特征，从图8可以得出结论：ω1影响的阶段较多，ω1越小，线状流段位置越高，礁核2中的天然气向礁盖1补给反映段的(第二个)凹子以及礁基3中的底水向礁核2能量补充反映段的(第三个)凹子越宽越深。
[0152]
改变礁核2的储容系数与总储容系数的储容比ω2，得到不同ω2下的无因次井底压力与压力导数的对比曲线，如图9所示，图9中两条平缓的曲线对应不同ω2下的无因次井底压力，区分不明显，凹凸不平的两条曲线对应不同ω2下压力导数，导数曲线更能够分辨储层特征，从图9可以得出结论：ω2主要影响第二个和第三个凹子，ω2越大(ω1不变，ω3减小)，导数曲线上第一个“凹子”基本不变，第二个凹子越宽越深，第三个凹子越浅越窄。
[0153]
由于礁盖1的储容系数与总储容系数的储容比ω1、礁核2的储容系数与总储容系数的储容比ω2、礁基3的储容系数与总储容系数的储容比ω3之和等于1，因此ω1、ω2变化时，ω3随之变化，这里不单独分析改变ω3时的情况。
[0154]
改变礁盖1中的天然裂缝和基质溶孔之间的窜流系数λ
m-f
，得到不同λ
m-f
下的无因次井底压力与压力导数的对比曲线，如图10所示，图10中两条平缓的曲线对应不同λ
m-f
下的无因次井底压力，区分不明显，凹凸不平的两条曲线对应不同λ
m-f
下压力导数，导数曲线更能够分辨储层特征，从图10可以得出结论：λ
m-f
主要影响第一个凹子出现的早晚，λ
m-f
越小，第一个凹子出现得越晚。
[0155]
改变礁盖1与礁核2之间的窜流系数λ
′
，得到不同λ
′
下的无因次压力与压力导数的对比曲线，如图11所示，图11中两条平缓的曲线对应不同λ
′
下的无因次井底压力，区分不明显，凹凸不平的两条曲线对应不同λ
′
下压力导数，导数曲线更能够分辨储层特征，从图11可以得出结论：λ
′
主要影响第二个凹子出现的早晚，λ
′
越小，第二个凹子出现得越晚。
[0156]
改变礁核2与礁基3之间的窜流系数λ
″
，得到不同λ
″
下的无因次井底压力与压力导数的对比曲线，如图12所示，图12中两条平缓的曲线对应不同λ
″
下的无因次井底压力，区分不明显，凹凸不平的两条曲线对应不同λ
″
下压力导数，导数曲线更能够分辨储层特征，从图12可以得出结论：λ
″
主要影响第三个凹子出现的早晚，λ
″
越小，第三个凹子出现得越晚。
[0157]
本发明的试井解释方法，充分考虑了礁基3(溶孔和弱底水)、礁核2(溶孔)、礁盖1(裂缝、溶孔)结构特征物性差异，以及酸压造缝的工况，同时将弱底水边界条件很好的融合到解释模型中，符合礁相气藏地质静态资料认识，弥补了常规试井解释方法无法描述生物礁气藏礁基3、礁核2、礁盖1结构特征及对弱底水的识别，导致地层信息挖掘量少，精度低、资料利用率低的不足，可以帮助测试技术人员充分认识生物礁气藏结构、底水特性以及开发动态，为气藏合理工作制度制定以及水处理提供指导，同时为提高该类型气藏勘探开发水平提供了一种新的解释方法。