一种机采系统效率软测量方法与流程

1.本发明涉及油田软测量技术领域，特别是一种机采系统效率软测量方法。


背景技术：

2.机采系统效率可反映油田的耗电量及能源利用效率，是评价抽油机井运行状况的一项重要经济技术指标，随着油田经营成本不断上升，精细化管理改革日益深入，准确计算系统效率对于采油厂掌握机采井的客观运行情况，优化节能设备投放比例，考核评价机采系统节能降耗技术效果，保证油田的持续稳产，提升综合管理水平，判断油田抽油机系统的潜力、研究油井生产对策有重要意义。
3.在油田实际生产中，进行机采系统效率计算常需获取各抽油机井的多项生产参数，部分参数无法实现每口井测取，参数缺失使得部分机组效率只能由部分已测井的效率数据来近似，此外，部分参数无法实现每日测量，如动液面、悬点载荷等参数测量需停机测量，测试工作强度大、耗时长，无法实时在线检测，影响油田生产进度，间接增加了采油厂的生产成本。
4.机采系统效率计算时依赖参数较多，某些参数难以测量，且机采系统效率与各影响参数存在非线性关系,常规方法难以有效剔除无关特征，通过局部线性嵌入与栈式自编码神经网络进行深度学习，得到机采系统原始数据的高阶特征，剔除无关信息，提取得到能够反映输出量大小的有效特征。
5.为解决上述问题，本方法提供了一种机采系统效率软测量方法，可规避机采系统某些参数难于测量以及参数与机采系统效率之间非线性问题，并进行高效特征提取。


技术实现要素：

6.为了解决现有的一些技术问题，本发明的主要目的是为了提供一种简单可行的机采系统效率软测量方法。
7.为达到上述目的，本发明提供了一种机采系统效率软测量方法的技术方案，该方法包括：
8.步骤1：采集多台建模样本的机采系统相关数据；
9.步骤2：对步骤1中的建模样本数据进行预处理；
10.步骤3：对预处理后的所有样本数据进行局部线性嵌入(lle)特征提取，并得到非线性特征空间；
11.步骤4：采用栈式自编码神经网络(sae)方法建立软测量模型。
12.步骤5：将待计算机采系统效率的抽油机井井况参数经过步骤2、步骤3得到降维后的核主成分后代入步骤4中建立的软测量模型，得到机采系统效率预测值。
13.上述方案中，步骤1中所述采集建模样本的机采系统相关数据，是在同一油田、不同时间采集不同抽油机井的井况数据。
14.上述方案中，步骤1的井况数据有回压、油管套压、含水率、原油密度、混合液密度、
产液量、日耗电量、泵深、泵径、冲程、冲次、平衡度、日运行时间、电机功率和功率因数。
15.上述方案中，步骤2中所述的预处理，是去除或降低不确定的信息对数据的噪声干扰，采用的预处理方法包括数据归一化处理、导数法处理、平滑处理或中心化及标准化处理。
16.上述方案中，步骤3中所述的进行局部线性嵌入(lle)提取，在保存原始高维数据邻域线性结构的基础上计算其低维表达。
17.上述方案中，步骤3中所述局部线性嵌入特征提取，得到降维特征向量，具体包括：
18.步骤31：对于原始数据
19.x＝[x1,x2,k,xn],d
×n[0020]
运用k近邻算法得到每个数据xi的k近邻点：
[0021]
ni＝knn(xi,k)ni＝[x
1i
，k，x
ki
]
[0022]
步骤32：求解如下有约束优化问题：
[0023][0024]
得权重系数矩阵：
[0025][0026]
si＝(x
i-ni)
t
(x
i-ni)
[0027][0028]
步骤33：求导得：
[0029][0030][0031]
步骤:34：求解有约束优化问题：
[0032][0033]
[0034]
得低维空间向量矩阵y：
[0035]
y＝[y1,y2,k,yn],d
×n[0036]
上述方案中，步骤4中所述栈式自编码神经网络方法可通过隐藏神经元环节稀疏性限制，获得一组基向量，并通过该组基向量反映输入向量本征结构，并建立回归模型，具体包括：
[0037]
步骤41：对于m个样本训练数据，将sigmoid函数作为单个神经元激活函数，得代价函数:：
[0038][0039]
x(i)：输入，y(i)：输出，前层与后层的连接权重，b：偏置值。
[0040]
步骤42：将作为为隐藏神经元j的激活度，计算均值：
[0041][0042]
步骤43:正则化：
[0043][0044][0045]
得总代价函数：
[0046][0047]
步骤44：计算自编码器输出及误差：
[0048][0049][0050]
步骤45：求偏导数：
[0051][0052][0053]
利用批量梯度下降法迭代更新参数w和b，求得网络最优解。
[0054]
所述步骤4中的栈式自编码神经网络的结构共分为5层，分别为1个输入层、3个隐藏层及1个输出层。
[0055]
从上述技术方案中可以看出，本发明具有以下有益效果：本发明针对机采系统某些关键参数难于测量的问题，将局部线性嵌入(lle)与栈式自编码神经网络(sae)相结合，建立了机采系统效率软测量模型。首先利用局部线性嵌入对样本数据进行特征提取，剔除
数据中的冗余信息，提取得到包含有效信息的主成分，达到特征降维的目的，然后利用sae建立机采系统效率的预测模型，并与其他常规建模方法进行对比试验。在一定程度上为采油单位优化生产提供了参数保证，是一种有效的软测量方法，能够在一定程度上帮助油田采油厂降低每月机采井效率测试的作业工作量和成本投入。
附图说明
[0056]
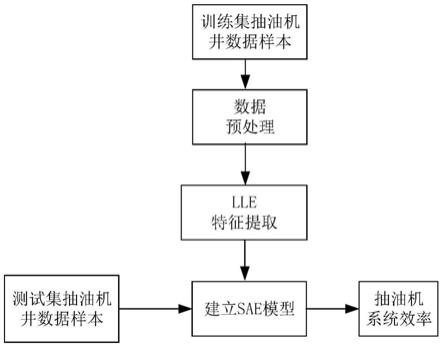
图1是本发明实施例1提供的机采系统效率软测量方法流程图。
[0057]
图2是实施例2中lle+sae预测值与真值散点图。
[0058]
图3是实施例3中机采系统效率预测值相对误差分布图。
具体实施方式
[0059]
为使本发明的目的、技术方案和优点更加清楚明白，以下结合具体实施例，并参照附图，对本发明进一步详细说明。
[0060]
实施例1
[0061]
本发明提供了一种机采系统效率软测量方法的技术方案，该方法包括：
[0062]
步骤1：采集多台建模样本的机采系统相关数据；
[0063]
步骤2：对步骤1中的建模样本数据进行预处理；
[0064]
步骤3：对预处理后的所有样本数据进行局部线性嵌入(lle)特征提取，并得到非线性特征空间；
[0065]
步骤4：采用栈式自编码神经网络(sae)方法建立软测量模型；其中，栈式自编码神经网络的结构共分为5层，分别为1个输入层、3个隐藏层及1个输出层；
[0066]
步骤5：将待计算机采系统效率的抽油机井井况参数经过步骤2、步骤3得到降维后的核主成分后代入步骤4中建立的软测量模型，得到机采系统效率预测值。
[0067]
上述方案中，步骤1中所述采集建模样本的机采系统相关数据，是在同一油田、不同时间采集不同抽油机井的井况数据。
[0068]
上述方案中，步骤1的井况数据有回压、油管套压、含水率、原油密度、混合液密度、产液量、日耗电量、泵深、泵径、冲程、冲次、平衡度、日运行时间、电机功率和功率因数。
[0069]
上述方案中，步骤2中所述的预处理，是去除或降低不确定的信息对数据的噪声干扰，采用的预处理方法包括数据归一化处理、导数法处理、平滑处理或中心化及标准化处理。
[0070]
上述方案中，步骤3中所述的进行局部线性嵌入(lle)提取，在保存原始高维数据邻域线性结构的基础上计算其低维表达。
[0071]
上述方案中，步骤3中所述局部线性嵌入特征提取，得到降维特征向量，具体包括：
[0072]
步骤31：对于原始数据
[0073]
x＝[x1,x2,k,xn],d
×n[0074]
运用k近邻算法得到每个数据xi的k近邻点：
[0075]
ni＝knn(xi,k)ni＝[x
1i
，k，x
ki
]
[0076]
步骤32：求解如下有约束优化问题：
[0077][0078]
得权重系数矩阵：
[0079][0080]
si＝(x
i-ni)
t
(x
i-ni)
[0081][0082]
步骤33：求导得：
[0083][0084][0085]
步骤:34：求解有约束优化问题：
[0086][0087][0088]
得低维空间向量矩阵y：
[0089]
y＝[y1,y2,k,yn],d
×n[0090]
上述方案中，步骤4中所述栈式自编码神经网络方法可通过隐藏神经元环节稀疏性限制，获得一组基向量，并通过该组基向量反映输入向量本征结构，并建立回归模型，具体包括：
[0091]
步骤41：对于m个样本训练数据，将sigmoid函数作为单个神经元激活函数，得代价函数:：
[0092][0093]
x(i)：输入，y(i)：输出，前层与后层的连接权重，b：偏置值。
[0094]
步骤42：将作为为隐藏神经元j的激活度，计算均值：
[0095][0096]
步骤43:正则化：
[0097][0098][0099]
得总代价函数：
[0100][0101]
步骤44：计算自编码器输出及误差：
[0102][0103][0104]
步骤45：求偏导数：
[0105][0106][0107]
利用批量梯度下降法迭代更新参数w和b，求得网络最优解。
[0108]
实施例2
[0109]
本发明提供了一种机采系统效率软测量方法，该方法分为六步来实现，图1是本发明提供的机采系统效率软测量方法流程图，该方法包括：
[0110]
首先，选取训练集样本，进行归一化预处理。选取lle的核参数，对归一化预处理后的数据lle特征提取，消除输入变量之间的相关性，提取包含有效信息，并降低特征空间的维数，再将提取得到的非线性主成分作为sae的输入，建立数学模型。而测试集用来检验所建模型的预测能力，将测试集样本带入模型计算，得到测试集样本所对应的预测结果。其中，在测试时，使用留一法来进行交叉验证，以检验所建模型的预测与泛化能力。
[0111]
实施例3
[0112]
图2是某一测试集的抽油机井系统效率的预测结果分布图，图中圆圈的分布越贴近红色斜线，说明预测结果越准确。从图2中可以看出，采用lle-sae软测量建模的输出预测值(软测量值)能够很好地跟踪抽油机井系统的真值(公式计算值)。
[0113]
图3是各抽油机井系统效率预测值相对误差分布图，由图可见预测值最大相对误差为8.2％，说明lle-sae的软测量模型能够较准确输出预测值。为检验lle-sae方法的预测性能，将该方法与其他几种常规的回归预测方法进行了对比试验。实验中使用了偏最小二乘回归(pls)、主成分回归(pcr)、主成分-支持向量机回归(pca-svr)、bp神经网络(bpann)等几种预回归测方法，并采用平均相对误差、相关系数和最大相对误差这3个预测性能的评
价指标来比较几种方法回归的预测效果。
[0114]
表1是根据留一法多次预测并取平均后得到的抽油机井系统效率模型预测值与抽油机井系统效率真值计算得到的指标，由表1可以看出lle-sae方法预测得到的抽油机井系统效率的最大相对误差为8.2％，平均相对误差为3.6％，相关系数为0.96，lle-sae方法为几种回归方法中的得到了性能指标最优，该方法所得预测值与真值具有较好的相关性，预测值具有较高的精度，可为油田生产提供可靠的参数依据。
[0115]
表1多种预测方法性能对比
[0116][0117]
以上所述的具体实施例，对本发明的目的、技术方案和有益效果进行了进一步详细说明，所应理解的是，以上所述仅为本发明的具体实施例而已，并不用于限制本发明，凡在本发明的精神和原则之内，所做的任何修改、等同替换、改进等，均应包含在本发明的保护范围之内。