一种飞行器载体的磁干扰补偿方法与流程

[0001]
本发明涉及飞行器磁环境优化技术领域，具体涉及一种飞行器载体的磁干扰补偿方法。


背景技术：

[0002]
飞行器载体(如飞机)内部的磁场环境是非常复杂的，空间梯度大，严重影响到内部的三轴矢量磁强计的测量准确度，增加了方向余弦获取的误差，导致背景磁场模型求解的失败。所以，需要对飞行器载体内部的磁环境进行磁干扰补偿。
[0003]
现有的磁干扰补偿模型存在求解困难、求解精度不够等问题；并且，目前在进行磁干扰补偿模型系数求解时，要求飞行器首先进行四航向机动学习飞行，用时几十分钟，然后将学习样本数据用于模型系数求解，这种方法不适合在要求快速反应的飞行器上使用。


技术实现要素：

[0004]
为了解决上述问题，本发明的目的在于提供一种飞行器载体的磁干扰补偿方法，包括如下步骤：
[0005]
一种飞行器载体的磁干扰补偿方法，包括如下步骤：
[0006]
s1，分别建立飞行器载体磁场的剩磁模型、感应磁场模型及涡流磁场模型，并将三者结合作为飞行器载体的总干扰磁场模型；
[0007]
s2，建立关于剩磁模型的剩磁参数、感应磁场模型的感磁参数及涡流磁场模型的涡流磁场参数的方程；
[0008]
s3，进行仿真试验，利用仿真试验结果及步骤s2中建立的方程，分别解得剩磁参数、感磁参数及涡流磁场参数，从而完成总干扰磁场模型的求解；
[0009]
s4，利用求解后的总干扰磁场模型，对飞行器的磁场数据测量值进行补偿。
[0010]
在一些实施例中，步骤s1中，建立剩磁模型的步骤包括：
[0011]
将剩磁表示为：h
p
＝{p
1 p
2 p3}
[0012]
则在测量点沿地磁矢量方向的投影为：
[0013][0014]
其中u
i
＝cosθ
i
为地磁矢量的方向余弦；
[0015]
建立感应磁场模型的步骤包括：
[0016]
将感应磁场在测量点处的矢量表示为：
[0017][0018]
沿地磁矢量方向的投影为：
[0019][0020]
其中：
[0021]
i≠j时
[0022]
a
11
＝(i
11-i
33
)b
[0023]
a
22
＝(i
22-i
33
)b
[0024]
令a
33
＝0，此时
[0025][0026]
建立涡流磁场模型的步骤包括：
[0027]
将感应磁场在测量点处的矢量表示为：
[0028][0029]
根据方向余弦的性质，有：u1u
′1+u2u
′2+u3u
′3＝0
[0030]
令：
[0031]
[0032]
则涡流磁场沿地磁矢量方向的投影可表达成：
[0033][0034]
因此，总干扰磁场模型为：
[0035][0036]
在一些实施例中，步骤s3中，采用三轴正交放置的线圈，通过计算机控制线圈驱动电流来产生三轴磁场矢量，以模拟飞行器的外部磁环境，从而完成仿真试验。
[0037]
在一些实施例中，步骤s3中，采用飞行器缩比模型来代替飞行器完成仿真试验。
[0038]
与现有技术相比，本发明提供的飞行器载体的磁干扰补偿方法，保证了模型参数求解的精度，在不同磁性状态下都能稳定求解，可以用于飞行器背景磁干扰实时补偿；且不依赖于机动飞行学习，省掉了飞行器的学习飞行时间，以保证装备的快速反应能力。
附图说明
[0039]
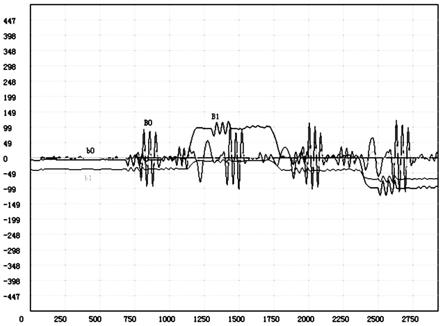
图1为利用本发明提供的飞行器载体的磁干扰补偿方法进行数据补偿后的效果图。
具体实施方式
[0040]
为使本发明的目的、技术方案和优点更加清楚，下面将对本发明的技术方案进行清楚、完整地描述。显然，所描述的实施例是本发明的一部分实施例，而不是全部的实施例。基于所描述的本发明的实施例，本领域普通技术人员在无需创造性劳动的前提下所获得的所有其他实施例，都属于本发明的保护范围。
[0041]
除非另外定义本发明使用的技术术语或者科学术语应当为本发明所属领域内具有一般技能的人士所理解的通常意义。
[0042]
本发明提供了一种飞行器载体的磁干扰补偿方法，包括如下步骤：
[0043]
s1，分别建立飞行器载体磁场的剩磁模型、感应磁场模型及涡流磁场模型，并将三者结合作为飞行器载体的总干扰磁场模型；
[0044]
s2，基于磁场小信号模型，建立关于剩磁模型的剩磁参数、感应磁场模型的感磁参数及涡流磁场模型的涡流磁场参数的方程；
[0045]
s3，进行仿真试验，利用仿真试验结果及步骤s2中建立的方程，分别解得剩磁参数、感磁参数及涡流磁场参数，从而完成总干扰磁场模型的求解；
[0046]
s4，利用求解后的总干扰磁场模型，对飞行器的磁场数据测量值进行补偿。
[0047]
具体地，步骤s1中，建立剩磁模型的步骤包括：
[0048]
将剩磁表示为：h
p
＝{p
1 p
2 p3}
[0049]
则在测量点沿地磁矢量方向的投影为：
[0050][0051]
其中u
i
＝cosθ
i
为地磁矢量的方向余弦；
[0052]
建立感应磁场模型的步骤包括：
[0053]
将感应磁场在测量点处的矢量表示为：
[0054][0055]
沿地磁矢量方向的投影为：
[0056][0057]
其中：
[0058]
i≠j时
[0059]
a
11
＝(i
11-i
33
)b
[0060]
a
22
＝(i
22-i
33
)b
[0061]
令a
33
＝0，此时
[0062][0063]
建立涡流磁场模型的步骤包括：
[0064]
将感应磁场在测量点处的矢量表示为：
[0065][0066]
根据方向余弦的性质，有：u1u
′1+u2u
′2+u3u
′3＝0令：
[0067][0068]
则涡流磁场沿地磁矢量方向的投影可表达成：
[0069][0070]
因此，总干扰磁场模型为：
[0071][0072]
在一个具体实施例中，建立方程的具体步骤如下：
[0073]
当飞机沿直线作小幅度机动时，有：
[0074]
u
i
(t)＝cos(θ
i0
+δθ
t
(t))
[0075]
ꢀꢀꢀꢀ
＝cosθ
i0
cosδθ
i
(t)-sinθ
i0
sinδθ
i
(t)
[0076]
ꢀꢀꢀꢀ
≈cosθ
i0-sinθ
i0
·
δθ
i
(t)
[0077]
近似有u
i
(t)＝u
i
+v
i
(t)；
[0078]
其中u
i
＝cosθ
i0
，v
i
(t)＝sinθ
i0
·
δθ(t)。
[0079]
由飞机机动所产生的磁场信号波动表示为：
[0080]
s(t)＝h
d
[u+v(t)]-h
d
(u)
[0081]
根据式(1)可得：
[0082]
[0083]
故有：
[0084]
规定坐标1正向为飞行器的机首方向，坐标2正向为右侧机翼方向，坐标3正向为垂直方向，向下为正；
[0085]
由得：
[0086][0087][0088][0089][0090][0091]
得到：
[0092]
s(t)＝w1v1+w2v2+w3v
′1+w4v
′2ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(2)
[0093][0094]
可见，式(3)中第一个式子是关于剩磁和感应磁场的，第二个式子是关于涡流磁场的；
[0095]
系数u
i
和w
i
与航向有关，称为航向系数，记不同航向下的系数为u
ik
和w
ik
，下标k表示航向序号；
[0096]
u
ik
:i＝1～3,k＝1～4；w
ik
:i＝1～2,k＝1～4
[0097]
沿四个航向飞行，可以建立四组方程，由此可得到关于剩磁和感应磁场的8个未知数方程：
[0098][0099]
同理，利用四个航向的航向系数，得到关于涡流磁场8个参数的方程如下：
[0100][0101]
利用方程(4)和方程(5)，结合步骤s3中的试验结果，即可解得剩磁参数p
i
、感磁参数a
ij
及涡流磁场参数b
ij
。
[0102]
进一步地，步骤s2中，具体还包括：
[0103]
对式(2)的两边做内积运算，并把左右位置对调，得：
[0104][0105]
其中：r
ij
＝r
ji
＝<v
i
,v
j
>，r
i+2j
＝r
ji+2
＝<v
′
i
,v
j
>i,j＝1,2，
[0106]
r
i+2j+2
＝r
j+2i+2
＝<v
′
i
,v
′
j
>i,j＝1,2，
[0107]
s
i
＝<s,v
i
>,s
i+2
＝<s,v
′
i
>i,j＝1,2；
[0108]
在小信号模型中，飞机在参考点附近作平面飞行，因此有：
[0109]
u
31
＝u
32
＝u
33
＝u
34
＝u3[0110]
此时，作变换：
[0111][0112]
则方程(4)可写成：
[0113][0114]
上述方程在正四边形航向，每个航向依次相差90
°
时，有：
[0115]
u
11
＝-u
13
，u
12
＝-u
14
，u
21
＝-u
23
，u
22
＝-u
24
[0116]
航向为0
°
，90
°
，180
°
，270
°
时，有：
[0117]
u
11
＝-u
13
，u
12
＝-u
14
＝0，u
21
＝-u
23
＝0，u
22
＝-u
24
[0118]
结合方程(6)先计算出四个航向的航向参数w
ij
，则方程(4)能够用固定次序求解，以得到剩磁参数p
i
和感磁参数a
ij
；
[0119]
或者航向为45
°
，135
°
，225
°
，315
°
时，有：
[0120]
u
11
＝u
14
，u
12
＝u
13
，u
11
＝-u
13
[0121]
u
21
＝u
22
，u
23
＝u
24
，u
21
＝-u
23
[0122]
方程(4)也能够用固定次序求解；
[0123]
航向为0
°
，90
°
，180
°
，270
°
时，有：
[0124]
u
11
＝-u
13
，u
12
＝-u
14
＝0，u
21
＝-u
23
＝0，u
22
＝-u
24
[0125]
方程(5)可以简化为：
[0126][0127]
方程(5)能够用固定次序求解，以得到涡流磁场参数b
ij
；
[0128]
或者，航向为45
°
，135
°
，225
°
，315
°
时，有：
[0129]
u
11
＝u
14
，u
12
＝u
13
，u
11
＝-u
13
[0130]
u
21
＝u
22
，u
23
＝u
24
，u
21
＝-u
23
[0131]
方程(5)也能够用固定次序求解。
[0132]
具体在求解时，可使飞行器在已知地磁场均匀的空域沿着一个方形的区域飞行，在保证飞行姿态不变的情况下，分别作小幅度的俯仰、横滚、偏航等3种机动动作，然后根据测得的磁场变化，利用上述的多个式子解得各个参数。
[0133]
可以理解的是，在中高纬度地区，当纬度不小于30
°
时，坐标3与地磁矢量的夹角不大于60
°
，有：u3＝cosγ≥0.5；u3作为系数中的分母，较大的取值不会引起太大的计算误差。但是，在低纬度地区，当纬度小于30
°
时，u3的值小于0.5，若u3取值太小，将其作为分母，会引起较大的计算误差，影响计算稳定性，此时可采用以下的改进方法：
[0134]
规定此时飞机飞行学习时，航向与南北方向的夹角小于60
°
，即：
[0135]-60
°
≤θ≤60
°
或120
°
≤θ≤240
°
[0136]
则有：u1＝cosα≥0.5，同样由：得：
[0137][0138]
[0139][0140][0141][0142]
与式(2)、式(3)类似地，可以得到：
[0143]
s(t)＝w1v2+w2v3+w3v
′2+w4v
′3[0144][0145]
上式中第一个式子是关于剩磁和感磁的，第二个式子是关于涡流磁场的。接下来，采用与前述类似的方法，一样能完成求解。
[0146]
可见，本发明使用小信号模型，采用剩磁系数、感磁系数与涡流磁场系数分开求解的方法，简化了对磁环境模拟的要求，保证模型参数求解的精度。
[0147]
优选地，为了使磁干扰补偿方法不依赖于机动飞行学习，省掉飞行器的学习飞行时间，以保证装备的快速反应能力，可采用仿真试验的方法来解算模型参数。
[0148]
在一个实施例中，可采用三轴正交放置的线圈，通过计算机控制线圈驱动电流来产生三轴磁场矢量，以模拟飞行器的外部磁环境，通过计算机软件完成仿真试验。为了求解各个参数，需要模拟飞行器在地磁场运动时所经历的外部磁场环境，使飞行器在地磁环境磁化下产生飞行器背景干扰磁场的数据样本，并生成关于模型参数的回归方程组，进而解出各个参数。
[0149]
具体地，前面的分析表明，飞行器干扰磁场可表示成：
[0150][0151]
其中：h1＝h
x
，h2＝h
y
，h3＝h
z
，p
i
为剩磁参数，a
ij
为感磁参数，b
ij
为涡流磁场参数。
[0152]
为了求解上式中的模型参数，需要模拟飞行器在地磁场运动时所经历的外部磁场环境，使飞行器在地磁环境磁化下产生飞行器背景干扰磁场的数据样本，并由式(1)生成关于模型参数的回归方程组，进而解出模型参数。
[0153]
三轴地磁矢量的模拟是采用三轴正交放置的线圈，通过计算机控制线圈驱动电流来产生三轴磁场矢量。由于三轴线圈存在安装误差，不是严格正交放置，因此产生的磁场矢量的三个分量，不仅与对应线圈的驱动电流有关，而且与其它两个线圈的驱动电流有关。为了描述磁场矢量与驱动电流的关系，对线圈的放置作如下限制：
①
z
′
轴线圈沿垂直方向放
置，磁场向下为正；
②
x
′
轴线圈沿南北方向放置，磁场向北为正；
③
y
′
轴线圈沿东西方向放置，磁场向东为正。
[0154]
由于线圈安置的误差，线圈轴线x
′
、y
′
、z
′
不能构成正交坐标系，故建立直角坐标系xyz，并且使得：
①
坐标z轴与z
′
轴线圈的轴线重合，向下为正；
②
坐标y轴与z
′
轴线圈和y
′
轴线圈的轴线共面，y轴向东为正；
③
坐标x轴垂直于y轴和z轴。因而也垂直于y
′
轴线圈轴线和z
′
轴线圈轴线，x轴向北为正。
[0155]
在上述计算坐标系中，磁场强度的三分量与各轴线圈驱动电流的关系如下：
[0156][0157]
称a
ij
为三轴线圈的电磁系数。h
xo
、h
yo
、h
zo
为本地地磁场在计算坐标系上的投影三分量。线圈电磁系数和本地地磁场分量均可以预先精确求出。
[0158]
为了精确模拟磁场矢量(h
x
,h
y
,h
z
)，对式(7)作线性变换如下：
[0159][0160]
其中
[0161][0162]
式(8)描述了线圈驱动电流(i
′
x
,i
′
y
,i
′
z
)与待模拟磁场(h
x
,h
y
,h
z
)的对应关系。据此，可以根据所要模拟的磁场精确确定线圈驱动电流。
[0163]
在载体坐标系中，所模拟固定点地磁矢量为：
[0164][0165]
其中，-90
°
≤θ≤90
°
，式(10)中，h为地磁场总强度，θ为相关于载体坐标系的磁倾角，为磁偏角。固定h值，改变θ和值，可以模拟飞行器在不同飞行姿态下受地磁场磁化的结果。
[0166]
为了使模型参数的求解结果稳定，θ、样本的选取应在其取值范围内均匀分布，但考虑到用于检测飞行器磁化状态的光泵磁强计存在测量盲区，与被测磁场矢量的夹角不能太小，也不能接近垂直。将光泵磁强计的光轴竖直取向，则要求，15
°
≤θ≤75
°
或-75
°
≤θ≤-15
°
。
[0167]
θ、样本点的选取如下：
[0168]
θ＝[-45
°
,-3
°°
,-15
°
,15
°
,30
°
,45
°
]
[0169][0170]
θ
i
，任意组合，构成48个样本数据再由式(10)计算得到48组磁场矢量样本数据
[0171]
令：n＝6m＝8
[0172]
记：k＝(i-1)n+j
[0173][0174]
由磁场样本数据，利用式(8)可获取相应的三轴线圈驱动电流
[0175][0176]
给三轴线圈加驱动电流(i
′
xk
,i
′
yk
,i
′
zk
)，产生模拟磁场(h
xk
,h
yk
,h
zk
)作用于飞行器壳体，产生飞行器在不同模拟姿态条件下的内部总磁场，使用光泵测出其大小{h
k
}
[0177]
此时飞行器壳体的背景磁场可表示如下：
[0178]
δh
k
＝h
k-h+δh
k
[0179]
δh
k
为进行k次样本试验时的日变修正量，可使用另一台光泵磁强计在一定距离外的参考测量点测量得到。
[0180]
以上进行磁化试验时，所加的磁场是静态磁场，产生的飞行器背景磁场中只有剩磁和感磁两部分。因此有：
[0181][0182]
其中
[0183][0184]
为地磁场方向余弦的样本值；p
i
(i＝1,2,3)为模型的剩磁系数；a
ij
＝a
ji
,a
33
＝0,i,j＝1,2,3为模型感磁系数。模型(13)中有8个独立变量。
[0185]
为了稳定求出模型的剩磁和感磁系数，必须有足够的测量样本数n
×
m，而且这些样本必须反应出地磁场从x、y、和z三个方向对飞行器磁化的信息，从定解最低要求出发，至少应选择磁倾角θ
j
的两个样本和磁方位角的四个样本，构成8个样本数据，但为了提高解的稳定性，样本数可选为独立变量数的5-10倍。一般情况下式(13)构成超定方程，可用线性
回归方法求解。
[0186]
飞行器只有在连续运动中，才产生涡流磁场，为了得到含有涡流磁场成份的飞行器背景磁场样本，必须将飞行器置于动态磁环境中。
[0187]
建立飞行器载体坐标系，坐标轴按x、y、z和1、2、3编号，其中轴1为纵轴，向前为正，轴2为横轴，向右为正，轴3为垂直轴，向下为正。当飞行器在均匀地磁场中作机动飞行时，地磁矢量在载体坐标的投影可表达成：
[0188][0189]
式(15)中{cosθ1,cosθ2,cosθ3}为地磁矢量在三个坐标轴上的方向余弦。
[0190]
为了求解涡流系数，使磁场产生器产生动态磁场作用于飞行器，模拟在不同磁纬度地区、不同磁航向上作小幅度俯仰、摇摆和横滚运动，使飞行器生成含有涡流磁场成份的背景磁干扰样本。
[0191]
a、俯仰运动模拟
[0192]
飞行器载体做小幅度俯仰运动，就是飞行器绕坐标轴y作小幅度旋转运动，为了信号模拟方便，将地磁场在飞行器载体上的投影三分量表达成：
[0193][0194]
式中cosθ2的几何意义与在式(15)相同，为地磁矢量在zx平面投影与轴z的夹角。若将地磁场在飞行器载体上的投影三分量按标准球坐标表示成：
[0195][0196]
式中，θ,为磁倾角和磁航向角，它们与式(16)中参量的关系为：
[0197][0198]
当飞行器载体作小幅度俯仰运动时，可选定：
[0199][0200]
式中，为俯仰角的小角度变化幅度，θ
2i
，为某次试验时，θ2,的平均取值。
[0201]
根据上面的结果，当需要模拟飞行器在地磁倾角和磁航向角为θ
i
、的状态下作小幅度俯仰运动时，可首先根据(18)式计算出θ
2i
和再根据式(16)和(19)产生待仿真的磁场。使用式(16)控制磁场产生，只需控制两轴同步，而不必控制三轴同步，控制方法简化，
容易保证控制精度。
[0202]
b、摇摆运动模拟
[0203]
飞行器载体做小幅度摇摆运动，就是飞行器绕坐标轴z作小幅度旋转运动，为了信号模拟方便，将地磁场在飞行器载体上的投影三分量表达成：
[0204][0205]
式中cosθ3的几何意义与在式(15)相同，为地磁矢量在xy平面投影与轴x的夹角。若将地磁场在飞行器载体上的投影三分量按标准球坐标表示成：
[0206][0207]
可知，θ3,即为磁倾角和磁航向角。
[0208]
当飞行器载体作小幅度摇摆运动时，可选定：
[0209][0210]
式中，为摇摆角的小角度变化幅度，θ
i
，为某次试验时，磁倾角和磁航向角的平均取值。
[0211]
根据上面的结果，当需要模拟飞行器在地磁倾角和磁航向角为θ
i
、的状态下作小幅度俯仰运动时，再根据式(20)和(22)产生待仿真的磁场。使用式(20)控制磁场产生时，同样只需控制两轴同步，而不必控制三轴同步，控制方法简化，容易保证控制精度。
[0212]
c、横滚运动模拟
[0213]
飞行器载体做小幅度横滚运动，就是飞行器绕坐标轴x作小幅度旋转运动，为了信号模拟方便，将地磁场在飞行器载体上的投影三分量表达成：
[0214][0215]
式中cosθ1的几何意义与在式(15)相同，为地磁矢量在yz平面投影与轴y的夹角。若将地磁场在飞行器载体上的投影三分量按标准球坐标表示成：
[0216][0217]
式中，θ,为磁倾角和磁航向角，它们与式(23)中参量的关系为：
[0218][0219]
当飞行器载体作小幅度横滚运动时，可选定：
[0220][0221]
式中，为横滚角的小角度变化幅度，θ
1i
，为某次试验时，θ1，的平均取值，
[0222]
根据上面的结果，当需要模拟飞行器在地磁倾角和磁航向角为θ
i
、的状态下作小幅度横滚运动时，可首先根据(26)式计算出θ
1i
和再根据式(24)和(25)产生待仿真的磁场。使用式(23)控制磁场产生，同样只需控制两轴同步，而不必控制三轴同步，控制方法简化，容易保证控制精度。
[0223]
在已求出飞行器感磁参数和剩磁参数的基础上，涡流参数方程如下：
[0224][0225]
其中，w
ij
,i,j＝1,2,3为模型涡流磁场系数，k为样本序号，w
33
＝0。令：
[0226][0227]
将信号及方向余弦写成小信号模式如下：
[0228]
u
ik
＝cosθ
ik
＝u
ik
+v
ik
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(29)
[0229]
s
k
(t)＝s
k0
+s
k
(t)
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(30)
[0230]
其中，u
ik
为某一直航线下u
ik
的平均值，s0为s
k
(t)的均值，由此得到(27)在小信号条件下模型系数方程为：
[0231][0232]
模型(27)中有8个独立变量，为了求解这一方程，只需在某一磁倾角θ条件下，选择四个航向，在每个航向里做两种小幅度机动，即可得到8个样本数据，构成对方程(31)的定解条件，磁倾角可选择中纬度地区的值，四个磁航向可分别选择为0
°
,90
°
,180
°
和270
°
，在0
°
和180
°
航向上作俯仰和摇摆机动，在90
°
和270
°
航向上，作横滚和摇摆运动。由此得到8个样本数据用于模型求解。
[0233]
试验结果分析：
[0234]
在一个具体实施例中，首先设定飞行器磁干扰补偿模型参数，用于模拟飞行器受地磁场磁化的规律，然后设定地磁场倾角和磁航向角，模拟飞行器的静态磁环境，再由模型生成飞行器在静态条件下的背景磁干扰数据，利用飞行器在静态条件下的背景磁干扰数据求解出飞行器磁干扰补偿模型的剩磁和感磁系数。
[0235]
然后，仿真生成飞行器四个航向的飞行器动态磁环境，仿真过程中，再利用飞行器磁干扰补偿模型，得到飞行器在动态条件下的背景磁干扰数据，用于求解飞行器磁干扰补
偿模型的涡流系数。在飞行器动态磁环境模拟中，为了更接近实际，对俯仰角、横滚角、摇摆角的模拟采用有一定频谱结构随机函数代替单一正弦波。仿真时，设定初始参数(飞行高度、速度、初始点磁场、坐标等)，由仿真计算函数产生磁场三轴分量、光泵数据。仿真时输入的已知参量包括：磁倾角φ、磁航向角θ、平均飞行高度h0、平均飞行速度v0、始点坐标x0＝0、始点磁场b0。
[0236]
根据飞行器背景磁干扰的仿真数据样本，对飞行器磁干扰模型参数进行求解，参数求解的结果及与真值对比如表1所示。
[0237]
表1模型参数求解结果
[0238][0239][0240]
上述参数求解结果与参数设定值对比表明，算法的稳定性和精度良好。模型的偏差不超过10％。
[0241]
此外，在另一个实施例中，也可以采用飞行器缩比模型来代替飞行器完成仿真试验。飞行器缩比模型的背景磁干扰的产生机理与实际飞行器相同，而其强度可控，因此能够模拟实际飞行器在地磁中磁化生成背景磁干扰的过程。实际试验时，将飞行器缩比模型放置在一个非磁性材料制作的支架上，依次使模型头部指向地理东、西、南和北四个方向，在每一方向上，用人工手动方法摇动飞行器缩比模型作俯仰、横滚和摇摆运动，并由安装在缩比模型内部的光泵和三轴磁强计采集背景磁干扰的样本数据。
[0242]
一个具体实施例中的飞行器载体磁干扰补偿结果曲线如图1所示。图中b0、b1分别表示补偿前和补偿后的波动曲线，b0和b1分别为b0和b1的局部放大。可以看出，补偿后的数据曲线比较平稳，几乎没有波动，基本上消除了航向误差，在实际工程应用中，如果在探测
区域内有磁性目标出现，那么在探测数据曲线图上一定是比较陡峭的波峰，很容易识别。通过对补偿前后数据曲线的波动大小进行处理分析，可以得出磁干扰补偿模型精度不低于90％，验证了补偿模型求解算法的良好磁环境适应性以及该试验方案的实际可行性，算法的稳定性和精度良好。
[0243]
综上，本发明提供的飞行器载体的磁干扰补偿方法，保证了模型参数求解的精度，在不同磁性状态下都能稳定求解，可以用于飞行器背景磁干扰实时补偿；且不依赖于机动飞行学习，省掉了飞行器的学习飞行时间，以保证装备的快速反应能力。
[0244]
以上所描述的具体实施例，对本发明的目的、技术方案和有益效果进行了进一步详细说明，应理解的是，以上所述仅为本发明的具体实施例而已，并不用于限制本发明，凡在本发明的精神和原则之内，所做的任何修改、等同替换、改进等，均应在本发明的保护范围之内。