基于图切地质平行剖面的基岩地质体三维模型构建方法及装置与流程

本发明涉及三维建模和地质学领域，尤其涉及一种基于图切地质平行剖面的基岩地质体三维模型构建方法及装置。

背景技术：

高效精确的三维地质建模方法研究，是有效利用地质勘察数据，提高地质体建模效率和建模质量的关键。地质构造的复杂性以及地质数据的不确定性、采样有限性(经济制约)，给三维地质建模带来巨大挑战。如何实现高效率、高质量的复杂地质体三维建模，始终是地质研究和应用中的难点和热点问题。

经过多年努力，国内外研究者已有针对性地提出了基于工程钻孔、地质剖面等的多种三维地质建模方法。然而，由于钻孔、物探成本的制约，相关建模方法主要是应用于数据基础良好、小范围、结构相对简单的工程地质体三维建模。对于复杂、广布的基岩地质体而言，由于建模数据匮乏和地质结构相对复杂，现有基于钻孔、剖面等数据的三维地质建模方法，无法直接进行大范围基岩地质体的三维建模。

地质图是将沉积岩层、火成岩体、地质构造等的形成时代和相关等各种地质体、地质现象，用一定图例表示在某种比例尺地形图上的一种图件。是表示地壳表层岩相、岩性、地层年代、地质构造、岩浆活动、矿产分布等的地图的总称。进一步，为了形象直观地感应填图区在垂向上的地层产状、接触关系及地质构造形态，在地形地质图完成后，可以在地质图上，选择某一方向，根据各种地质、地理要素，按一定的比例尺，用投影方法切绘生成图切地质剖面。图切地质剖面同地质图相配合，二者可以反映地质构造在空间上的相互关系，蕴含了丰富的三维地质建模信息。经过地学工作者的长期努力，全覆盖、多尺度的地质图数据已基本具备，全自动、高质量的图切地质剖面生成方法也已成熟。如果基于数字地质图，在制作一系列平行的图切地质剖面的基础上，能够进行大范围基岩地质体的三维建模，则具有重要的研究意义和实用价值。

技术实现要素：

发明目的：本发明针对现有技术存在的问题，提供一种高效精确的基于图切地质平行剖面的基岩地质体三维模型构建方法。

技术方案：本发明所述的基于图切地质平行剖面的基岩地质体三维模型构建方法包括：

(1)分别根据二维图切地质平行剖面矢量数据和基点数据表生成二维图切剖面集合s和基点集合at；

(2)从二维图切剖面集合s中获取任意两个相邻二维图切剖面si、si+1，并根据属于si、si+1的地层构建地层对集合cou；

(3)从cou任取一地层对couj，根据地层对couj构建每个地层对应的边界线集合al、边界线集合bl；

(4)基于基点集合at，将边界线集合al与bl从二维转换为三维；

(5)判断地层对couj中两个地层是否都为连续地层，若是执行步骤(6)；否则执行步骤(7)；

(6)基于三维边界线集合al与bl，采用morphing三边法构建连续地质体三维模型；

(7)基于三维边界线集合al与bl，采用morphing三边法构建尖灭地质体三维模型；

(8)循环执行步骤(3)-(7)，直至完成集合cou中所有地层对的遍历，得到所有地层对的地质体三维模型；

(9)循环执行步骤(2)-(8)，直至完成所有相邻二维图切剖面的遍历，得到所有相邻二维图切剖面间的地质体三维模型。

进一步的，步骤(1)包括：

(1-1)读取二维图切地质平行剖面矢量数据，生成二维图切剖面集合s＝{si|i＝1,2,…,ni}，其中si代表第i个二维图切剖面，ni代表二维图切剖面数量；

(1-2)读取基点数据表，生成基点集合at＝{αi(xi,yi,θ)|i＝1,2,…,ni},其中αi表示第i个基点，与si对应，xi为横坐标，yi为纵坐标，θ为方位角。

进一步的，步骤(2)包括：

(2-1)从二维图切剖面集合s中获取任意两个相邻二维图切剖面si、si+1；

(2-2)分别读取si、si+1中的所有地层，构建si的地层集合as＝{stia,stib,stic,…}与si+1的地层集合bs＝{st(i+1)a,st(i+1)b,st(i+1)c,…}，其中，a,b,c为区域地层的统一地层编码，该信息来自图切剖面中地层要素的地层编码属性；

(2-3)从集合as中获取任一地层stir，并遍历集合bs，查找其中是否存在地层编码为r的地层，若存在，则表示无尖灭，从集合bs获取该地层st(i+1)r，构建地层对cou＝[stir、st(i+1)r]，执行步骤(2-5)；若不存在，代表地层stir存在右端尖灭，执行步骤(2-4)；

(2-4)在集合as中，不断搜索地层stir的邻近地层，直至找到一个在集合as、bs中共同存在的地层st(i+1)x，并构建地层对cou＝[stir、st(i+1)x]；

(2-5)返回执行步骤(2-3)，直至集合as被遍历完；

(2-6)查找集合bs中是否存在未配对地层，若存在未配对地层st(i+1)r，则代表该地层左端尖灭，从集合bs中获取配对地层不断搜索地层st(i+1)r的邻近地层，直至找到一个在集合as、bs中共同存在的地层stix，并构建地层对cou＝[stix、st(i+1)r]；

(2-7)将所有地层对存入地层对集合cou＝{couj(cou,flag)|j＝1,2,…,nj}，其中，couj代表第j个地层对元素，nj代表地层对数量，flag代表尖灭类型，当flag＝0表示无尖灭，为连续地层；flag＝-1代表存在右端尖灭的地层；flag＝1代表存在左端尖灭的地层。

进一步的，步骤(3)包括：

(3-1)从地层对集合cou中获取任一地层对couj，并分别获取couj中每个地层的中心点与轮廓线linea、lineb；

(3-2)分别离散轮廓线linea、lineb，得到linea、lineb的节点集合其中，是linea的第u个离散点，nu是linea离散点数，是lineb的第v个离散点，nv是lineb离散点数；

(3-3)根据节点集合sa和sb构建集合其中，

(3-3)根据矢量叉积方法将轮廓线linea与轮廓线lineb的绕行方向同步为顺时针；

(3-4)按顺序从集合ap中读取任意连续的三个节点apu-1、apu与apu+1，计算三点顺时针夹角的角度φ，若φ∈[270,360)，代表点apu为轮廓线linea上的一个转折点，记为pk，在pk处打断轮廓线linea，得到边界线alk＝linea(pk-1,pk)，其中，pk-1表示上,次查找到的转折点，若k＝1，则pk-1＝ap1，linea(pk-1,pk)表示从linea上获取从点pk-1到pk之间的线；若φ∈[0,270)，则代表点apu为非转折点，继续获取节点；

(3-5)重复执行步骤(3-4)，直至集合ap所有连续的三个节点被遍历，将得到所有边界线存入边界线集合al＝{alk|k＝1,2,…,an},其中，an代表边界线数量；

(3-6)对边界线集合al有序化处理；具体方法为：获取边界线集合al中含有最小纵坐标值点的边界线alk；以边界线alk为参考线，从边界线集合al寻找以边界线alk终点为起点的边界线alt，并将边界线alt调整为边界线集合al的首要素；再以边界线alt为参考线，重复上述步骤，依次进行集合al中要素排序，直到边界线al内全部要素排序完毕；

(3-7)按照步骤(3-4)-(3-6)，构建轮廓线lineb边界线集合bl＝{blk|k＝1,2,…,bn},其中，bn代表边界线数量；

(3-8)获取地层对couj中存储的尖灭类型flag，若flag＝0，执行步骤(3-9)；否则执行步骤(4)；

(3-9)计算边界线集合al、bl间的边界线数量差值co＝an-bn，若co＝0，则代表边界线一一对应，执行步骤(4)；若co>0，代表集合al中边界线多于集合bl，执行步骤(3-10)；若co<0，代表集合al中边界线少于集合bl，执行步骤(3-11)；

(3-10)按长度比例分割集合bl中边界线要素blbn/2，具体方法为：计算集合al中边界线alan/2-1、alan/2与alan/2+1长度分别占三者总长度的比例ηan/2-1、ηan/2与ηan/2+1；按照比例ηan/2-1、ηan/2与ηan/2+1分割集合bl中边界线blbn/2，得到三条线，分别记为blbn/2-1、blbn/2与blbn/2+1；将分割后的新边界线blbn/2-1、blbn/2与blbn/2+1替换掉集合bl中边界线要素blbn/2，并按从前到后的顺序更新边界线序号；

(3-11)按照步骤(3-10)方法，分割边界线集合al中边界线alan/2。

进一步的，步骤(4)包括：

(4-1)根据基点集合at获取二维图切剖面si的对应基点αi(xi,yi,θ)，xi为αi横坐标，yi为αi纵坐标，θ为αi方位角；

(4-2)获取边界线集合al中任一边界线alk，得到边界线alk的二维离散点集合其中，cpl代表边界线alk的第l个离散点，nl代表二维离散点数量；

(4-3)根据下式将二维离散点集合cp转换到三维，构建三维节点集合

(4-4)基于三维节点集合ep，构建三维边界线alk；

(4-5)循环执行步骤(4-2)-(4-3)，直至边界线集合al中所有边界线被遍历，完成al中所有边界线的三维转换；

(4-6)基于二维图切剖面si+1与对应基点αi+1，根据步骤(4-2)-(4-5)，完成边界线集合bl内所有边界线的三维转换。

进一步的，步骤(6)包括：

(6-1)从集合al、bl中分别获取任意对应边alk、blk,分别获取alk、blk起点starta(xta,yta,zta)、startb(xtb,ytb,ztb)，并以starta、startb作为起点、终点构建线lineab；

(6-2)分别获取alk、blk,的离散点集合其中，epl是alk的第l个离散点，nl代表alk离散点数量，fpg是blk的第g个离散点，ng代表blk离散点数量；

(6-3)计算count＝nl-ng，若count>0，则在集合fp中每两点之间插入一中点，直到插入|count|个点，使得ng＝nl；若count<0，则在集合ep中每两点之间插入一中点，直到插入|count|个点,使得nl＝ng；

(6-4)以集合ep对应的边界线alk为起始地质界线、集合fp对应的边界线blk为目标地质界线、lineab为约束边，基于morphing三边法构建地层面点集合surface；

(6-5)以地层面点集合surface为基础数据构建不规则三角面，形成三维地层面tink；

(6-6)循环执行步骤(6-1)-(6-5)，直至完成集合al、bl所有对应边的遍历，得到三维地层面集合tin＝{tink|k＝1,2,…,an}；

(6-7)分别以集合al、bl的边界线封闭成多面体polygona、polygonb；

(6-8)将polygona、polygonb与集合tin中所有三维地层面镶嵌在一起，形成单一三维地质体rockr。

进一步的，步骤(6-4)包括：

(6-4-1)基于约束边lineab的起点starta和终点startb，在lineab上进行插值，并根据下式计算各插值点的z坐标，形成z值集合cz＝{czo|o＝1,2,…,pcn}，其中，czo表示第o个插值点的z坐标，pcn是插值点数目；

(6-4-2)分别从插入点后的集合ep和fp中获取一组对应点epl、fpg，l＝g，在两点之间插入pcn个点，根据下式计算各插入点的坐标，并存入插值点集合其中，xpo代表epl、fpg之间插入的第o个点；

(6-4-3)将点epl、fpg分别插入到集合xp首位与末位，并将集合xp存储至地层面点集合surface中；

(6-4-4)循环执行步骤(6-4-2)-(6-4-3)，直至集合ep和fp中所有对应点被遍历，得到地层面点集合surface。

进一步的，步骤(7)包括：

(7-1)获取地层对couj存储的尖灭类型flag，若flag＝1，执行步骤(7-2)；若flag＝-1执行步骤(7-8)；

(7-2)获取集合al的中间边界线alan/2与集合bl中末位边界线blbn；

(7-3)基于morphing三边法构建alan/2与blbn之间的地层面点集合surfacel＝{xplt|t＝1,2,…,nt}；其中，xplt＝{xple|e＝1,2,…,pcln}，xplt表示使用morphing三边法形成的surfacel中第t个子集，xple是xplt中第e个点，pcln是点数目，nt是子集数目；

(7-4)从surfacel交替获取点xpl1[xplpcln/2]、xpl2[xplpcln/2+1]、xpl3[xplpcln/2+2]、…、xplt[xplpcln/2+10]、xplt+1[xplpcln/2+9]、…、xplm[xplpcln/2]，存入参考点集合rp中，并基于集合rp构建参考线referl，其中，m表示子集序号；

(7-5)从集合bl中获取任一边界线blk，以参考线referl为起始地质界线、边界线blk为目标地质界线，线referl与线blk起点连线为约束边，基于morphing三边法构建地层面点集合surfacell；

(7-6)以地层面点集合surfacell为基础数据构建不规则三角面，形成三维地层面tinlk；

(7-7)循环执行步骤(7-5)-(7-6)，直至完成集合bl所有边被遍历，得到三维地层面集合tinl＝{tinlk|k＝1,2,…,bn}；bn为三维地层面数目；

(7-8)将集合bl的边界线封闭成的多面体polygonb，与集合tinl中所有三维地层面镶嵌，形成单一三维地质体rockx；

(7-9)对于右端尖灭地层，获取集合bl中间边界线blbn/2与集合al中末位边界线要素alan，按照步骤(7-3)-(7-8)同样操作，得到单一三维地质体rockx。

本发明所述的基于图切地质平行剖面的基岩地质体三维模型构建装置，包括处理器及存储在存储器上并可在处理器上运行的计算机程序，所述处理器执行所述程序时实现上述方法。

有益效果：本发明与现有技术相比，其显著优点是：本发明自动化程度高，既提高了基岩地质体三维模型的建模效率，又具有较高的精确度。

附图说明

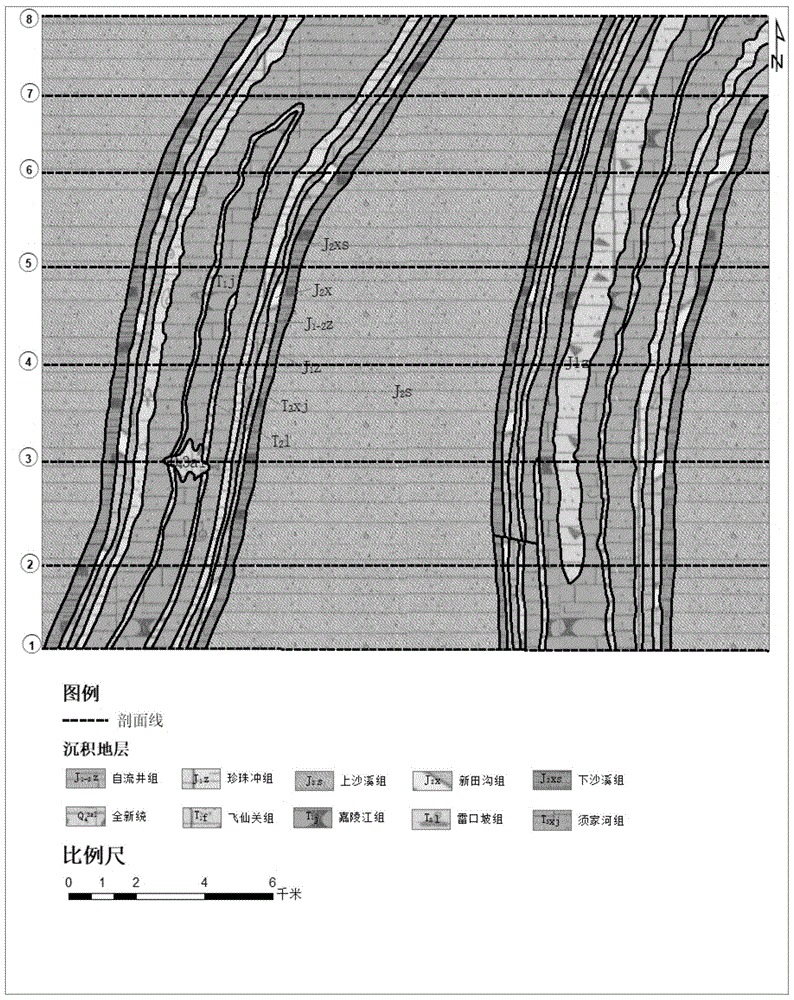
图1是本发明实施例中采用的剖面线与地质数据示意图；

图2是本发明实施例中采用的基点数据表；

图3是本发明提供的基于图切地质平行剖面的基岩地质体三维模型构建方法的流程图；

图4是二维图切剖面示意图(剖面线①)；

图5是三维剖面序列示意图；

图6是morphing三边法示意图；

图7是单一三维基岩地质体rock2示意图；

图8是基岩地质体三维模型((b)为正视图，(a)、(c)为侧视图)。

具体实施方式

下面对本发明技术方案作进一步详细的说明，本实施例的实验数据采用的是中国1：20万重庆h48-23图幅地质图数据(图1)与剖面线基点数据表(图2)，该实验数据采用的投影坐标系为beijing_1954。下面结合附图，并通过描述一个具体的实施例，来进一步说明。

如图3所示，本实施例提供的基于图切地质平行剖面的基岩地质体三维模型构建方法包括：

(1)分别根据二维图切地质平行剖面矢量数据和基点数据表生成二维图切剖面集合s和基点集合at。

该步骤具体包括：

(1-1)读取二维图切地质平行剖面矢量数据，生成二维图切剖面集合s＝{si|i＝1,2,…,ni}，其中si代表第i个二维图切剖面，ni代表二维图切剖面数量；在本实施例中，ni＝8；

(1-2)读取基点数据表，生成基点集合at＝{αi(xi,yi,θ)|i＝1,2,…,ni},其中αi表示第i个基点，与si对应，xi为横坐标，yi为纵坐标，θ为方位角。

(2)从二维图切剖面集合s中获取任意两个相邻二维图切剖面si、si+1，并根据属于si、si+1的地层构建地层对集合cou。

该步骤具体包括：

(2-1)从二维图切剖面集合s中获取任意两个相邻二维图切剖面si、si+1；在本实施例中，在i＝1时二维图切剖面s1如图4所示；

(2-2)分别读取si、si+1中的所有地层，构建si的地层集合as＝{stia,stib,stic,…}与si+1的地层集合bs＝{st(i+1)a,st(i+1)b,st(i+1)c,…}，其中，a,b,c为区域地层的统一地层编码，该信息来自图切剖面中地层要素的地层编码属性；

(2-3)从集合as中获取任一地层stir，并遍历集合bs，查找其中是否存在地层编码为r的地层，若存在，则表示无尖灭，从集合bs获取该地层st(i+1)r，构建地层对cou＝[stir、st(i+1)r]，执行步骤(2-5)；若不存在，代表地层stir存在右端尖灭，执行步骤(2-4)；

(2-4)在集合as中，不断搜索地层stir的邻近地层，直至找到一个在集合as、bs中共同存在的地层st(i+1)x，并构建地层对cou＝[stir、st(i+1)x]；

(2-5)返回执行步骤(2-3)，直至集合as被遍历完；

(2-6)查找集合bs中是否存在未配对地层，若存在未配对地层st(i+1)r，则代表该地层左端尖灭，从集合bs中获取配对地层不断搜索地层st(i+1)r的邻近地层，直至找到一个在集合as、bs中共同存在的地层stix，并构建地层对cou＝[stix、st(i+1)r]；

(2-7)将所有地层对存入地层对集合cou＝{couj(cou,flag)|j＝1,2,…,nj}，其中，couj代表第j个地层对元素，nj代表地层对数量，flag代表尖灭类型，当flag＝0表示无尖灭，为连续地层；flag＝-1代表存在右端尖灭的地层；flag＝1代表存在左端尖灭的地层。

(3)从cou任取一地层对couj，根据地层对couj构建每个地层对应的边界线集合al、边界线集合bl。

该步骤具体包括：

(3-1)从地层对集合cou中获取任一地层对couj，并分别获取couj中每个地层的中心点与轮廓线linea、lineb；

(3-2)分别离散轮廓线linea、lineb，得到linea、lineb的节点集合其中，是linea的第u个离散点，nu是linea离散点数，是lineb的第v个离散点，nv是lineb离散点数；

(3-3)根据节点集合sa和sb构建集合其中，

(3-3)根据矢量叉积方法将轮廓线linea与轮廓线lineb的绕行方向同步为顺时针；所述矢量叉积方法，公开在下列文件:philipj.s.,davidh.e.,geometrictoolsforcomputergraphics,elsevierscience,2003,p64-65.

(3-4)按顺序从集合ap中读取任意连续的三个节点apu-1、apu与apu+1，计算三点顺时针夹角的角度φ，若φ∈[270,360)，代表点apu为轮廓线linea上的一个转折点，记为pk，在pk处打断轮廓线linea，得到边界线alk＝linea(pk-1,pk)，其中，pk-1表示上,次查找到的转折点，若k＝1，则pk-1＝ap1，linea(pk-1,pk)表示从linea上获取从点pk-1到pk之间的线；若φ∈[0,270)，则代表点apu为非转折点，继续获取节点；

(3-5)重复执行步骤(3-4)，直至集合ap所有连续的三个节点被遍历，将得到所有边界线存入边界线集合al＝{alk|k＝1,2,…,an},其中，an代表边界线数量；

(3-6)对边界线集合al有序化处理；具体方法为：获取边界线集合al中含有最小纵坐标值点的边界线alk；以边界线alk为参考线，从边界线集合al寻找以边界线alk终点为起点的边界线alt，并将边界线alt调整为边界线集合al的首要素；再以边界线alt为参考线，重复上述步骤，依次进行集合al中要素排序，直到边界线al内全部要素排序完毕；

(3-7)按照步骤(3-4)-(3-6)，构建轮廓线lineb边界线集合bl＝{blk|k＝1,2,…,bn},其中，bn代表边界线数量；

(3-8)获取地层对couj中存储的尖灭类型flag，若flag＝0，执行步骤(3-9)；否则执行步骤(4)；

(3-9)计算边界线集合al、bl间的边界线数量差值co＝an-bn，若co＝0，则代表边界线一一对应，执行步骤(4)；若co>0，代表集合al中边界线多于集合bl，执行步骤(3-10)；若co<0，代表集合al中边界线少于集合bl，执行步骤(3-11)；

(3-10)按长度比例分割集合bl中边界线要素blbn/2，具体方法为：计算集合al中边界线alan/2-1、alan/2与alan/2+1长度分别占三者总长度的比例ηan/2-1、ηan/2与ηan/2+1；按照比例ηan/2-1、ηan/2与ηan/2+1分割集合bl中边界线blbn/2，得到三条线，分别记为blbn/2-1、blbn/2与blbn/2+1；将分割后的新边界线blbn/2-1、blbn/2与blbn/2+1替换掉集合bl中边界线要素blbn/2，并按从前到后的顺序更新边界线序号；

(3-11)按照步骤(3-10)方法，分割边界线集合al中边界线alan/2。

(4)基于基点集合at，将边界线集合al与bl从二维转换为三维。在本实施例中，所有三维剖面如图5所示。

该步骤具体包括：

(4-1)根据基点集合at获取二维图切剖面si的对应基点αi(xi,yi,θ)，xi为αi横坐标，yi为αi纵坐标，θ为αi方位角；

(4-2)获取边界线集合al中任一边界线alk，得到边界线alk的二维离散点集合其中，cpl代表边界线alk的第l个离散点，nl代表二维离散点数量；

(4-3)根据下式将二维离散点集合cp转换到三维，构建三维节点集合

(4-4)基于三维节点集合ep，构建三维边界线alk；

(4-5)循环执行步骤(4-2)-(4-3)，直至边界线集合al中所有边界线被遍历，完成al中所有边界线的三维转换；

(4-6)基于二维图切剖面si+1与对应基点αi+1，根据步骤(4-2)-(4-5)，完成边界线集合bl内所有边界线的三维转换。

(5)判断地层对couj中两个地层是否都为连续地层，若是执行步骤(6)；否则执行步骤(7)。

(6)基于三维边界线集合al与bl，采用morphing三边法构建连续地质体rockr三维模型。在本实施例中，morphing三边法如图6所示。

该步骤具体包括：

(6-1)从集合al、bl中分别获取任意对应边alk、blk,分别获取alk、blk起点starta(xta,yta,zta)、startb(xtb,ytb,ztb)，并以starta、startb作为起点、终点构建线lineab；

(6-2)分别获取alk、blk,的离散点集合其中，epl是alk的第l个离散点，nl代表alk离散点数量，fpg是blk的第g个离散点，ng代表blk离散点数量；

(6-3)计算count＝nl-ng，若count>0，则在集合fp中每两点之间插入一中点，直到插入|count|个点，使得ng＝nl；若count<0，则在集合ep中每两点之间插入一中点，直到插入|count|个点,使得nl＝ng；

(6-4)以集合ep对应的边界线alk为起始地质界线、集合fp对应的边界线blk为目标地质界线、lineab为约束边，基于morphing三边法构建地层面点集合surface；

(6-5)以地层面点集合surface为基础数据构建不规则三角面，形成三维地层面tink；

(6-6)循环执行步骤(6-1)-(6-5)，直至完成集合al、bl所有对应边的遍历，得到三维地层面集合tin＝{tink|k＝1,2,…,an}；

(6-7)分别以集合al、bl的边界线封闭成多面体polygona、polygonb；

(6-8)将polygona、polygonb与集合tin中所有三维地层面镶嵌在一起，形成单一三维地质体rockr。其中，镶嵌方法基于arcgisengineapi实现。在本实施例中，当i＝1、r＝2时，构建单一三维基岩地质体rock2如图7所示。

其中，步骤(6-4)包括：

(6-4-1)基于约束边lineab的起点starta和终点startb，在lineab上进行插值，并根据下式计算各插值点的z坐标，形成z值集合cz＝{czo|o＝1,2,…,pcn}，其中，czo表示第o个插值点的z坐标，pcn是插值点数目；

(6-4-2)分别从插入点后的集合ep和fp中获取一组对应点epl、fpg，l＝g，在两点之间插入pcn个点，根据下式计算各插入点的坐标，并存入插值点集合其中，xpo代表epl、fpg之间插入的第o个点；

(6-4-3)将点epl、fpg分别插入到集合xp首位与末位，并将集合xp存储至地层面点集合surface中；

(6-4-4)循环执行步骤(6-4-2)-(6-4-3)，直至集合ep和fp中所有对应点被遍历，得到地层面点集合surface。

(7)基于三维边界线集合al与bl，采用morphing三边法构建尖灭地质体rockx三维模型。

该步骤具体包括：

(7-1)获取地层对couj存储的尖灭类型flag，若flag＝1，执行步骤(7-2)；若flag＝-1执行步骤(7-8)；

(7-2)获取集合al的中间边界线alan/2与集合bl中末位边界线blbn；

(7-3)基于morphing三边法构建alan/2与blbn之间的地层面点集合surfacel＝{xplt|t＝1,2,…,nt}；其中，xplt＝{xple|e＝1,2,…,pcln}，xplt表示使用morphing三边法形成的surfacel中第t个子集，xple是xplt中第e个点，pcln是点数目，nt是子集数目；其中，本步骤surfacel的获取方法与步骤(6-4)的方法相同，参照步骤(6-4)即可；

(7-4)从surfacel交替获取点xpl1[xplpcln/2]、xpl2[xplpcln/2+1]、xpl3[xplpcln/2+2]、…、xplt[xplpcln/2+10]、xplt+1[xplpcln/2+9]、…、xplm[xplpcln/2]，存入参考点集合rp中，并基于集合rp构建参考线referl，其中，m表示子集序号；

(7-5)从集合bl中获取任一边界线blk，以参考线referl为起始地质界线、边界线blk为目标地质界线，线referl与线blk起点连线为约束边，基于morphing三边法构建地层面点集合surfacell；其中，本步骤surfacell的获取方法与步骤(6-4)的方法相同，参照步骤(6-4)即可；

(7-6)以地层面点集合surfacell为基础数据构建不规则三角面，形成三维地层面tinlk；

(7-7)循环执行步骤(7-5)-(7-6)，直至完成集合bl所有边被遍历，得到三维地层面集合tinl＝{tinlk|k＝1,2,…,bn}；bn为三维地层面数目；

(7-8)将集合bl的边界线封闭成的多面体polygonb，与集合tinl中所有三维地层面镶嵌，形成单一三维地质体rockx；其中，镶嵌方法基于arcgisengineapi实现；

(7-9)对于右端尖灭地层，获取集合bl中间边界线blbn/2与集合al中末位边界线要素alan，按照步骤(7-3)-(7-8)同样操作，得到单一三维地质体rockx。

(8)循环执行步骤(3)-(7)，直至完成集合cou中所有地层对的遍历，得到所有地层对的地质体三维模型。

(9)循环执行步骤(2)-(8)，直至完成所有相邻二维图切剖面的遍历，得到所有相邻二维图切剖面间的地质体三维模型。

在本实施例中，基于重庆h48-23图幅地质图，生成的基岩地质体三维模型如图8所示。本发明实施例中基于arcgisengineapi提供部分gis操作，相关步骤也可以使用supermap、arcgisobject等软件的api进行相应gis操作。

本实施例还提供了一种基于图切地质平行剖面的基岩地质体三维模型构建装置，包括处理器及存储在存储器上并可在处理器上运行的计算机程序，所述处理器执行所述程序时实现上述方法。

以上所揭露的仅为本发明一种较佳实施例而已，不能以此来限定本发明之权利范围，因此依本发明权利要求所作的等同变化，仍属本发明所涵盖的范围。