一种基于VMD和BLS组合模型的风电功率预测方法与流程

一种基于vmd和bls组合模型的风电功率预测方法
技术领域
[0001]
本发明涉及风电技术领域，尤其是涉及一种基于vmd和bls组合模型的风电功率预测方法。


背景技术：

[0002]
目前来看，风电功率预测的方法有物理方法、时间序列法和人工智能方法。人工智能方法包括人工神经网络(ann)和支持向量机(svm)等。
[0003]
目前大多数模型都是在支持向量机或神经网络的基础上结合其他算法进行组合预测得到预测功率。如经验模态分解(elm)或小波变换与支持向量机的组合对风功率进行预测,预测效果不是很好。
[0004]
上述方法中svm和ann对风电功率进行预测精度不高，小波变换中小波基的选取与分解尺度的确定比较困难，经验模态分解易使分解数据模态混叠、出现端点效应现象，影响预测的精度。


技术实现要素：

[0005]
本发明的目的就是为了克服上述现有技术存在的缺陷而提供一种基于vmd和bls组合模型的风电功率预测方法，首先对原始风功率时间序列进行变分模态分解，然后通过对分解后的k个有限带宽本证模态分量(bimf)分别bls回归预测，最后将各分量预测结果进行线性叠加得到最终预测结果。
[0006]
本发明的目的可以通过以下技术方案来实现：
[0007]
一种基于vmd和bls组合模型的风电功率预测方法，该方法包括以下步骤：
[0008]
步骤1：收集风电功率数据，并进行训练样本和测试样本的选取；
[0009]
步骤2：对采集到的风电功率数据进行vmd变分模态分解，得到vmd分解风电功率序列；
[0010]
步骤3：将vmd分解风电功率序列中的各个模态分量输入至bls模型中进行预测，得到各个模态分量对应的bls模型输出量；
[0011]
步骤4：对所有模态分量对应的bls模型输出量叠加求和，得到最终的组合模型预测的风电功率结果，并进行误差计算；
[0012]
进一步地，所述的步骤2包括以下分步骤：
[0013]
步骤201：构造约束变分模型；
[0014]
步骤202：对约束变分模型对应的约束问题中引入拉格朗日乘子和惩罚因子，将其转变为非约束的变分问题；
[0015]
步骤203：利用交替方向乘子法求解非约束的变分问题对应式子中的鞍点，获得相应变量的更新公式；
[0016]
步骤204：确定更新迭代的停止条件后，对采集到的风电功率数据进行vmd变分模态分解，得到vmd分解风电功率序列。
[0017]
进一步地，所述的步骤201中的约束变分模型，其对应的数学描述公式为：
[0018][0019]
式中，δ(t)表示单位脉冲函数，*表示卷积，表示偏导，u
k
(t)表示k个分量，{w
k
}表示k个bimf分量的中心频率，{u
k
}表示k个bimf分量，f(t)表示风电功率的时间数据，e-jwkt
表示单边际谱的指数信号。
[0020]
进一步地，所述的步骤202中的非约束的变分问题，其对应的数学描述公式为：
[0021][0022]
式中，α表示惩罚因子，λ表示拉格朗日乘子。
[0023]
进一步地，所述的步骤203中的相应变量的更新公式，其对应的数学描述公式为：
[0024][0025][0026][0027]
式中，上标∧表示傅里变换，n为迭代次数，o表示更新因子。
[0028]
进一步地，所述的步骤204中的更新迭代的停止条件，其对应的数学描述公式为：
[0029][0030]
式中，∈表示判别精度。
[0031]
进一步地，所述的步骤3中的bls模型采用高斯核函数代替增强节点的激活函数，所述高斯核函数，其对应的数学描述公式为：
[0032][0033]
所述高斯核函数对应的核矩阵，其对应的数学描述公式为：
[0034][0035]
所述bls模型的输出，其对应的数学描述公式为：
[0036]
y＝[z,k(x
i
,x
j
)]w
[0037]
式中，r为核参数，ω
bls
表示核矩阵，h表示增强层的输出，y表示宽度学习系统bls的输出，w表示输出层的权重，z表示特征层的输出，x
i
和x
j
分别为输入样本中的任意两个数据，h(x
i
)和h(x
j
)分别为输入样本中的任意两个数据所对应的增强层的输出，k(x
i
,x
j
)表示输入样本中的任意两个数据所对应的高斯核函数，ω
bls
(i,j)表示输入样本中的任意两个数据所对应的核矩阵。
[0038]
进一步地，所述的步骤4中的误差计算所采用的方法包括平均绝对误差mae、均方误差mse以及平均绝对百分误差mape。
[0039]
进一步地，所述的均方误差mse，其描述公式为：
[0040][0041]
式中，y
i
为实际值，为预测值。
[0042]
进一步地，所述的平均绝对百分误差mape，其描述公式为：
[0043][0044]
式中，y
i
为实际值，为预测值。
[0045]
与现有技术相比，本发明具有以下优点：
[0046]
(1)本发明技术方案通过对vmd和bls模型的组合，克服分解时模态混叠和端点效应现象同时有效降低了风功率时间序列的随机性和间歇性对预测模型的影响，有效的应对风电功率的非平稳性，通过vmd分解为平稳信号进行预测。效果要好于单一模型直接对风功率进行预测。
[0047]
(2)本发明技术方案基于变分模态分解(vmd)和宽度学习(bls)的相关理论，提出一种新的短期风功率组合预测模型。该方法为解决单一模型预测误差比较大的情形。同时改善了模型的预测效果，适用于多变量、非线性、小样本的短期风功率预测。实践证明：组合预测模型较单一预测模型能够优势互补，提高预测精度和增强模型的鲁棒性。
[0048]
(3)本发明技术方案创新性的采用了vmd和bls新组合预测模型。，较单一预测模型，本技术方案通过vmd和bls组合的模型预测方法，可以有效的提高风电功率预测精度，降低风电并网的不确定性带来的损失。
附图说明
[0049]
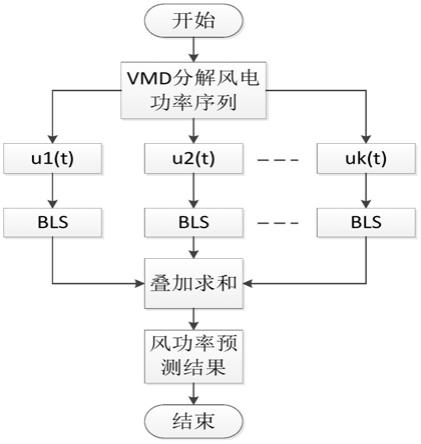
图1为本发明的整体方法流程图；
[0050]
图2为本发明整体方法中的vmd算法流程图；
[0051]
图3为本发明方法实施例中风电功率的原始序列示意图；
[0052]
图4为本发明方法实施例中风电功率的原始序列经过vmd分解后的结果示意图；
[0053]
图5为本发明方法实施例中采用本发明方法的模型预测结果比对示意图。
具体实施方式
[0054]
下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例是本发明的一部分实施例，而不是全部实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动的前提下所获得的所有其他实施例，都应属于本发明保护的范围。
[0055]
具体实施例
[0056]
本发明的预测方法，具体过程如图1所示，包括：
[0057]
第一阶段：变分模态对风电功率
[0058]
对原始风电功率时间序列进行vmd分解，将具有非线性、随机性的原始风电功率序列分解为一系列平稳的模态分量。
[0059]
第二阶段：对各模态分量分别进行预测
[0060]
对各子模态分别建立bls回归预测模型进行预测。
[0061]
第三阶段：叠加求和
[0062]
叠加各子模态预测值，得到最终的风电功率预测结果。
[0063]
具体实施过程如下：
[0064]
i、首先进行数据的收集。
[0065]
如图3所示，选取采样间隔为15min的北研风电场连续96天数据、共8064组风电功率数据作为vmd-bls组合预测模型试验数据样本进行预测，前7864组数据作为训练样本，后200组数据作为测试样本，输入变量为8维，分别是风电功率前2小时的历史数据，输出变量为1维，就是需要预测的风电功率。
[0066]
ii、对采集到的数据进行变分模态分解。
[0067]
为了应对风电功率的非平稳性，如图2所示，通过vmd对其分解为不同中心频率{w
k
}＝{w1,w2,
…
w
k
}的平稳信号{u
k
}＝{u1,u2,
…
u
k
}。vmd本质为约束性变分问题，通过约束变分模型，将原始风功率序列分解为k个具有特定稀疏性的bimf分量{u
k
}，如图4所示，为了获取bimf分量，首先通过hilbert变换求得各分量u
k
的单边际谱并估计各分量的中心频率w
k
，将单边际谱与其指数信号e-jwkt
相乘使得模态的频谱调制到相应基频带，最后计算解析信号梯度平方l2范数。目标是使得各bimf的估计带宽和最小，限定约束条件为各分量之和等于原始信号f(t)。构造约束变分模型为：
[0068][0069]
式中，δ(t)表示单位脉冲函数，*表示卷积，表示偏导，u
k
(t)表示k个分量，{w
k
}表示k个bimf分量的中心频率，{u
k
}表示k个bimf分量，f(t)表示风电功率的时间数据，e-jwkt
表示单边际谱的指数信号。
[0070]
对上式(1)中的约束问题引入拉格朗日(lagrange)乘子λ和惩罚因子α，将其变为非约束的变分问题，其表达式如下：
[0071][0072]
式中，α表示惩罚因子，λ表示拉格朗日乘子。
[0073]
利用交替方向乘子法(admm)求解(2)式中的鞍点，获得相应变量u
k
、w
k
、λ的更新公式分别为：
[0074][0075][0076][0077]
式中，上标∧表示傅里变换，n为迭代次数，o表示更新因子。
[0078]
vmd分解时，更新迭代的停止条件为：
[0079][0080]
式中，∈表示判别精度。
[0081]
iii、通过改进的bls模型进行预测。
[0082]
将vmd分解的{u
k
}＝{u1,u2,
…
u
k
}个模态分量，将u
k
作为输入数据然后通过bls模型分别对其预测，将u
k
中前8维的风电功率数据作为输入x
i
，将u
k
中后一维的风电功率数据作为输出y
i
。
[0083]
令输入训练样本{x
i
,y
i
},其中输入样本x
i
,i＝1,
…
,l。输出样本y
i
,i＝1,
…
,l。x
i
为训练特征，y
i
为训练目标。宽度学习的具体训练过程为：
[0084]
对样本x
i
进行特征映射z
i
＝φ(x
i
w
ei
+β
ei
),i＝1,
…
,l.其中w
ei
和β
ei
为随机产生的权重和偏置。
[0085]
将特征层的输出表示为：
[0086]
z
l
＝[z1,
…
,z
l
]
ꢀꢀ
(7)
[0087]
并将m组增强节点表示为：
[0088]
q
m
＝θ(z
l
w
lm
+β
lm
)
ꢀꢀ
(8)
[0089]
θ为增强节点的非线性激活函数，w
lm
、β
lm
为特征层输出给增强层随机产生的权重和偏置。将增强层的输出用h表示，则h＝[h1,
…
,h
m
]。
[0090]
改进的bls为高斯核函数代替增强节点的激活函数，将输入样本数据映射到高维特征空间。激活函数φ选取高斯核函数为：
[0091][0092]
式中：r为核参数。
[0093]
核矩阵ω
bls
如下：
[0094][0095]
用w表示输出层的权重，则上述宽度学习系统的输出可以表示为：
[0096]
y＝[z,k(x
i
,x
j
)]w
ꢀꢀ
(11)
[0097]
通过求伪逆的方式，求得w＝[z,k(x
i
,x
j
)]
+
y至此宽度学习系统训练完毕，具体预测结果如图5所示。
[0098]ⅳ、对预测结果进行误差计算。
[0099]
对其预测的结果叠加求和，得到最终的组合模型预测的风功率结果。对结果利用平均绝对误差(mae)，均方误差(mse)，以及平均绝对百分误差(mape)进行衡量。
[0100][0101][0102]
式中，y
i
为实际值，为预测值。
[0103]
具体各预测模型预测结果评价指标如表1所示：
[0104]
表1各预测模型预测结果评价指标
[0105][0106]
以上所述，仅为本发明的具体实施方式，但本发明的保护范围并不局限于此，任何
熟悉本技术领域的技术人员在本发明揭露的技术范围内，可轻易想到各种等效的修改或替换，这些修改或替换都应涵盖在本发明的保护范围之内。因此，本发明的保护范围应以权利要求的保护范围为准。