一种道岔变截面钢轨导波传播特性确定方法与流程

1.本发明涉及钢轨道岔技术领域，具体地说，涉及一种道岔变截面钢轨导波传播特性确定方法。


背景技术：

2.导波是指由于结构边界的存在所形成的具有多模式性和频散特性的弹性波。导波的本质是一种在固体结构中传播的应力波，在弹性固体波动学中，通常将具有一定形状和边界的能够对应力波的传播方向进行引导的固体介质称为波导。导波在结构中传播的机理研究是导波理论的基础，对于基于导波的结构健康监测技术的成熟应用至关重要，是后续研究工作开展的基石。基于导波的结构健康监测是一种有前途的技术，可以连续监测并识别结构伤损。但由于道岔直尖轨沿线路纵向具有变截面特征，对于该结构的导波传播特性研究仍然是比较困难。
3.频散曲线不仅可以用来描述不同频率下的导波在波导介质中的传播特性、导波速度，还可以用于指导导波无损检测试验，例如导波模态的选取、激励频率的选择以及模态辨识等。由于钢轨横截面几何形状复杂，无法像横截面规则的弹性体一样得到频散方程，要获得钢轨中导波的频散曲线只能采用数值方法，将波动方程转化成频域方程，然后通过引入合适的位移和应力边界条件，求解频域方程的特征值，进而求得频散曲线。
4.弹性波在截面缓慢变化的波导中的传播是现有研究中的一个难点，因为波模式的频散特性不仅随频率变化，而且随截面变化而改变。这意味着波数、相速度和群速度，对于每种波模式都连续变化。目前没有有效的数值方式可以得到变截面直尖轨的频散关系，无法指导尖轨伤损检测。


技术实现要素：

5.本发明的内容是提供一种道岔变截面钢轨导波传播特性确定方法，其能够克服现有技术的某种或某些缺陷。
6.根据本发明的一种道岔变截面钢轨导波传播特性确定方法，其包括以下步骤：
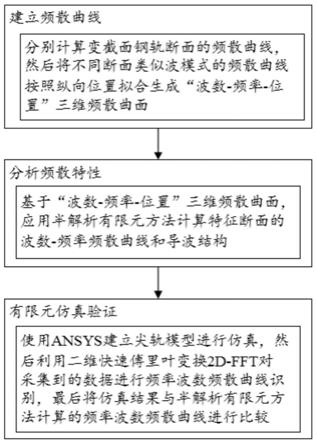
7.一、建立频散曲线：分别计算变截面钢轨断面的频散曲线，然后将不同断面类似波模式的频散曲线按照纵向位置拟合生成“波数-频率-位置”三维频散曲面；
8.二、分析频散特性：基于“波数-频率-位置”三维频散曲面，应用半解析有限元方法计算特征断面的波数-频率频散曲线和导波结构；
9.三、有限元仿真验证：使用ansys建立尖轨模型进行仿真，然后利用二维快速傅里叶变换2d-fft对采集到的数据进行频率波数频散曲线识别，最后将仿真结果与半解析有限元方法计算的频率波数频散曲线进行比较。
10.作为优选，步骤一中，首先将变截面道岔钢轨沿纵向划分成n-1(n≥1)段，然后分别计算变截面钢轨n个断面的频散曲线。
11.作为优选，步骤三中，仿真过程中，在直尖轨顶宽端面的网格加载垂向激励信号，
激励信号为hanning窗调制的中心频率为30khz的10周期正弦波信号。
12.作为优选，步骤三中，距离激励位置0.32m和1.32m范围内，每隔4毫米设置一组数据采集阵列，然后利用二维快速傅里叶变换2d-fft对采集到的数据进行频率波数频散曲线识别。
13.作为优选，半解析有限元方法为：
14.设钢轨为各向同性的，波在x方向上传播，在y-z平面上有等截面；可用空间分布函数来表示钢轨中任意一点的位移，表示如下：
[0015][0016]
式中：k为波数，w为频率，虚数单位
[0017]
应用有限元法建立了单元质量矩阵和刚度矩阵，并将其组合成整体矩阵和自由谐波振动的矩阵特征值问题；
[0018]
[k1+ikk2+k2k
3-w2m]u＝0；
[0019]
式中k
n
(n＝1,2,3)是与波数相关的矩阵，m是质量矩阵，u代表特征向量；可以通过在等式中指定一个实际波数并求解特征值问题来计算传播模式，以获得实数频率和振型；
[0020]
或者，为了计算特定频率下的波数，方程组可以被布置为：
[0021][0022][0023]
式中0表示大小为m
×
m的零矩阵；等式产生m个正向和m个反向特征值对的2m个特征值输出；计算出的特征值可以是实数，复数或虚数；复数和虚数特征值表示渐逝模式，而实数特征值表示选定频率下的传播模式；群速度计算公式如下所示：
[0024][0025]
本发明的技术效果如下：
[0026]
1.本发明把道岔钢轨分为n个特征断面并利用半解析有限元方法计算其三维频散曲面，节省了计算时间；
[0027]
2.考虑到钢轨道岔连续变截面的特点，通过选取道岔钢轨的特殊断面研究其频散曲线，可以得到整个道岔钢轨的频散曲面以及频散特性；
[0028]
3.通过仿真验证的结果，证明了该方法应用在变截面道岔钢轨的有效性，为检测弹性波在变截面钢轨传播提供了有效的理论指导。
附图说明
[0029]
图1为实施例1中一种道岔变截面钢轨导波传播特性确定方法的流程图；
[0030]
图2为实施例1中三维频散曲面的示意图；
[0031]
图3为实施例1中波数-频率频散曲线的示意图；
[0032]
图4为实施例1中波数-频率频散曲线的另一示意图；
[0033]
图5为实施例1中mode1波结构的示意图；
[0034]
图6为实施例1中mode2波结构的示意图；
[0035]
图7为实施例1中30khz下不同波数对应波结构的示意图；
[0036]
图8为实施例1中尖轨模型的示意图；
[0037]
图9为实施例1中激励信号的示意图；
[0038]
图10为实施例中节点激励仿真的示意图；
[0039]
图11为实施例1中仿真后频率波数频散曲线的示意图。
具体实施方式
[0040]
为进一步了解本发明的内容，结合附图和实施例对本发明作详细描述。应当理解的是，实施例仅仅是对本发明进行解释而并非限定。
[0041]
实施例1
[0042]
如图1所示，本实施例提供了一种道岔变截面钢轨导波传播特性确定方法，其包括以下步骤：
[0043]
一、建立频散曲线：分别计算变截面钢轨断面的频散曲线，然后将不同断面类似波模式的频散曲线按照纵向位置拟合生成“波数-频率-位置”三维频散曲面；如图2所示；
[0044]
二、分析频散特性：基于“波数-频率-位置”三维频散曲面，应用半解析有限元方法计算特征断面的波数-频率频散曲线和导波结构；
[0045]
三、有限元仿真验证：使用ansys建立尖轨模型进行仿真，然后利用二维快速傅里叶变换2d-fft对采集到的数据进行频率波数频散曲线识别，最后将仿真结果与半解析有限元方法计算的频率波数频散曲线进行比较。
[0046]
波导结构的频散特性与截面形式有着直接的关系，考虑到高速道岔变截面钢轨实际截面沿纵向连续缓慢变化的特征，在局部表现与等截面钢轨相似的弹性波传播特性，经过对不同位置各断面频散曲线的求解，发现相近断面之间的频散曲线基本一致，对于截面连续变化的变截面钢轨，其频散特性沿波导纵向连续缓慢变化；因此，步骤一中，首先将变截面道岔钢轨沿纵向划分成n-1(n≥1)段，横断面间距应保证能够反映钢轨断面的纵向连续变化特征，然后分别计算变截面钢轨n个断面的频散曲线。
[0047]
在频散曲面中，可以反映出不同位置断面的频散曲线以及相似波模式频散特性沿纵向的变化规律，结合频散曲面上的“波数-频率-位置”点对应的波结构，进一步对弹性波在变截面钢轨中的传播规律进行研究。
[0048]
以18号高速道岔直尖轨为例，其变截面区段全长11792mm，顶宽由0mm过渡为72.2mm，以顶宽5mm为步长截取特征断面，基于半解析有限元方法，求解各特征断面的频散曲线。此处选取了道岔尖轨铣削加工过程中的两个关键控制断面的频散曲线进行对比分析，其顶宽分别为30mm和35mm，断面形式及其频散曲线如图3所示，不同尖轨断面对应的导波模式及其在30khz处的导波结构如图4、图5和图6所示。
[0049]
由图3可知，相似断面对应的波数-频率频散曲线相似。选取导波模式1和导波模式2对变截面直尖轨的频散特性进行说明，由图4(a)和图5可以看出，导波模式1对应轨底的导波结构相似，不同尖轨断面变形位置处的形状和材料参数相同，所以导波模式1对应的频散
曲线没有产生变化。由图4(b)和图6可以看出，导波模式2对应的频散曲线随着尖轨断面的变化而缓慢变化，导波结构也缓慢变化。
[0050]
应用半解析有限元方法计算尖轨顶宽35mm断面的波数-频率频散曲线和导波结构。图7中显示了尖轨顶宽35mm断面在30khz处的导波结构，采用rainbow图例表示，不同导波模式对应的颜色比例一致。mode1至mode9主要变现为面内变形，mode10至mode15主要变现为面外变形。
[0051]
步骤三中，使用ansys建立尖轨模型(尖轨顶宽30mm至40mm)，如图8所示。本实施例采用8节点实体网格对道岔3d实体单元模型进行网格划分，网格大小为导波波长的1/10。
[0052]
步骤三中，仿真过程中，在直尖轨顶宽端面的网格加载垂向激励信号，激励信号为hanning窗调制的中心频率为30khz的10周期正弦波信号，如图9所示。
[0053]
步骤三中，距离激励位置0.32m和1.32m范围内，每隔4毫米设置一组数据采集阵列，有251个数据采集节点，如图10所示，然后利用二维快速傅里叶变换2d-fft对采集到的数据进行频率波数频散曲线识别。
[0054]
仿真结果与半解析有限元方法计算的频率波数频散曲线进行了比较，如图11所示。2d-fft的结果与对应模式的频率-波数曲线吻合良好，图11(a)结果对应图6中的mode6，图11(b)结果对应图6中的mode1。证明了此理论分析方法对于连续变截面钢轨频散特性的研究得到了良好理论验证。
[0055]
半解析有限元方法为：
[0056]
在半解析有限元方法中，仅对波导的横截面进行有限元离散，对传播方向进行解析处理。该方法能够高效地计算导波频散特性，但需要假设沿传播方向的钢轨横截面几何形状和材料特性是恒定的。设钢轨为各向同性的，波在x方向上传播，在y-z平面上有等截面；可用空间分布函数来表示钢轨中任意一点的位移，表示如下：
[0057][0058]
式中：k为波数，w为频率，虚数单位
[0059]
应用有限元法建立了单元质量矩阵和刚度矩阵，并将其组合成整体矩阵和自由谐波振动的矩阵特征值问题；
[0060]
[k1+ikk2+k2k
3-w2m]u＝0；
[0061]
式中k
n
(n＝1,2,3)是与波数相关的矩阵，m是质量矩阵，u代表特征向量；可以通过在等式中指定一个实际波数并求解特征值问题来计算传播模式，以获得实数频率和振型；
[0062]
或者，为了计算特定频率下的波数，方程组可以被布置为：
[0063][0064][0065]
式中0表示大小为m
×
m的零矩阵；等式产生m个正向和m个反向特征值对的2m个特征值输出；计算出的特征值可以是实数，复数或虚数；复数和虚数特征值表示渐逝模式，而
实数特征值表示选定频率下的传播模式；群速度计算公式如下所示：
[0066][0067]
以上示意性的对本发明及其实施方式进行了描述，该描述没有限制性，附图中所示的也只是本发明的实施方式之一，实际的结构并不局限于此。所以，如果本领域的普通技术人员受其启示，在不脱离本发明创造宗旨的情况下，不经创造性的设计出与该技术方案相似的结构方式及实施例，均应属于本发明的保护范围。