基于物理中性面的功能梯度复合材料无网格SPH分析模型的制作方法

基于物理中性面的功能梯度复合材料无网格sph分析模型
技术领域
[0001]
本发明涉及复合材料分析技术领域，具体涉及一种基于物理中性面的功能梯度复合材料无网格sph分析模型。


背景技术：

[0002]
功能梯度材料(fgb)能在高温高压等恶劣环境下工作而备受关注，功能梯度材料结构件的变性问题成为研究热点。由于双向功能梯度材料梁或板的材料属性在长度和厚度方向均有变化，导致中性面和中间面并不重合，传统基于中间面的梁板理论不能准确预测该材料的变形。


技术实现要素：

[0003]
本发明的目的在于提供一种基于物理中性面的功能梯度复合材料无网格sph分析模型，以解决现有技术中存在的技术问题。
[0004]
为实现上述目的，本发明采用的技术方案是：一种基于物理中性面的功能梯度复合材料无网格sph分析模型，所述分析模型的建立方法包括如下步骤：步骤(1)：基于泰勒级数展开式的对称sph即ssph方法对sph方法进行改进；步骤(2)：确定双向fg梁的中性面位置，建立基于精确中性面位置的三阶reddy-bickford梁板理论，推导由两种或四种不同材料组成的fgb的控制方程，并利用ssph方法对该控制方程进行离散；步骤(3)：对双向功能梯度复合材料进行弯曲变形的计算，利用文献中已有解和自编有限元程序求解结果，验证分析模型的正确性。
[0005]
可选实施例中，所述步骤(1)具体为：对于具有连续导数到(n+1)阶的函数u(x)，通过泰勒级数展开，利用函数值及其在邻近点x
i
上的导数逼近函数在x
j
上的值，
[0006][0007]
忽略四阶以上的项，式(1)可以写成矩阵形式为
[0008]
u(x)＝a(x
i
,x
j
)q(x
i
)
ꢀꢀꢀ
(1)
[0009]
其中，
[0010][0011]
a(x
i
,x
j
)＝[1,x
j-x
i
,(x
j-x
i
)2,(x
j-x
i
)3,(x
j-x
i
)4]
[0012]
作为向量q(x
i
)的元素，函数u的核估计及其在x处的导数是由式(1)得到的未知量，为此，将式(1)两边同时乘以w(x
i
,x
j
)a(x
i
,x
j
)
t
，得到
[0013][0014]
式中w(x
i
,x
j
)为核函数，确定该点的紧支域；x
i
到x
j
的距离越小，核函数的值越大；
[0015]
使用最广泛的三次b样条函数，
[0016][0017]
其中h定义为平滑长度或核长度，s＝|x
j-x
i
|/h；
[0018]
对在x
i
的支持域中的每个相邻粒子x
j
，计算式(2)，并对公示的两边求和，得到
[0019][0020]
其中，n
i
为在x
i
的支持域中的临近粒子x
j
的个数；
[0021]
由式(3)，可计算出向量q
[0022][0023]
其中，
[0024][0025]
最后，通过式(4)中向量q中的5个元素，使用缩写形式，可以估计出函数及其一阶到四阶的导数
[0026][0027]
可选实施例中，所述步骤(2)包括：长度为l、厚度为h的矩形功能梯度复合材料梁fgb，承受横向均布力q；双向fgb的材料性能沿x-长度)和z-厚度方向连续变化，服从幂律函数；
[0028]
考虑由两种和四种不同材料组成的双向fgb；
[0029]
第一种情况，梁由陶瓷和金属组成，有效材料特性p随厚度和长度的变化而变化，
[0030][0031]
式中，n
x
和n
z
分别为材料性能随梁长和梁厚变化的梯度指数；
[0032]
第二种情况，假设梁由陶瓷1、陶瓷2和金属1、金属2组成，其体积分数v在轴向和横向上的变化如下:
[0033][0034]
其中，下标c1、c2、m1和m2分别表示组成成分:陶瓷1、陶瓷2、金属1和金属2；
[0035]
梁的材料特性p可以用voigt模型表示为
[0036]
p＝p
c1
v
c1
+p
c2
v
c2
+p
m1
v
m1
+p
m2
v
m2
[0037]
其中p
c1
、p
c2
、p
m1
、p
m2
分别为陶瓷1、陶瓷2、金属1、金属2的性能；得到材料的杨氏模量e、剪切模量g性质，如下:
[0038][0039]
其缩写形式为：
[0040]
可选实施例中，所述步骤(2)还包括：基于rbt，梁任意点的轴向位移和横向位移可表示
[0041][0042]
w(x,z)＝w0(x)
[0043]
其中u、w分别表示沿x、z方向的位移，w0为梁中间表面点的横向变形，φ(x)为横截面的旋转，α＝4/3h2；
[0044]
由于杨氏模量在厚度方向和长度方向同时变化，中间面与中性面不重合，公式(5)不能准确描述双向fgb的挠度行为；因此，应将物理中性面与rbt相结合，则位移场可表示为
[0045][0046]
w(x,z)＝w0(x)
[0047]
参数z0，c2定义为
[0048][0049]
z0为物理中性面与中间面之间的距离，将式(6)代入式(7)，得到:
[0050][0051][0052]
显然，对于均质的或是仅在x方向连续变化的或常规fgb，由于n
z
为零，物理中性面与中间面重合；
[0053]
由动力学方程可得轴向线性应变和剪切应变:
[0054][0055]
其中，β＝3α＝4/h2。
[0056]
可选实施例中，所述控制方程建立过程为：用轴向应力和轴向应变表示的梁的虚拟应变能δu可以表示为
[0057][0058]
其中δ为变分算子，a为梁的横截面面积，σ
xx
为正应力，σ
xz
为横向剪应力；应用胡克定律，可以计算出应力，
[0059][0060]
将公式(6),(8)和(10)带入式(9)，可得
[0061][0062]
其中，
[0063][0064]
横向荷载q的虚势能为
[0065][0066]
应用虚位移原理δw＝δu+δv＝0，得到
[0067][0068]
因此，可以得到平衡方程
[0069][0070]
将式(11)代入式(12)，四种材料的fgb的rbt控制方程可以表示为
[0071][0072][0073]
其中包括如下定义，
[0074][0075][0076][0077][0078]
可选实施例中，所述离散化过程为：
[0079]
利用式(5)中函数及其一阶至四阶导数的ssph表示，四种不同材料构成的双向fgb的平衡方程可离散为如下两式，
[0080]
[0081][0082][0083]
本发明的有益效果在于：
[0084]
(1)本发明中的基于物理中性面的功能梯度复合材料无网格sph分析模型采用基于泰勒级数展开式的对称sph即ssph方法对传统的sph方法进行改进，克服了传统sph方法存在边界缺陷计算精度差的缺点，提高了计算精度。
[0085]
(2)本发明中的基于物理中性面的功能梯度复合材料无网格sph分析模型确定了双向fg梁的中性面位置，建立了基于精确中性面位置的三阶reddy-bickford梁板理论，推导了由两种或四种不同材料组成的fgb的控制方程，并用ssph方法对控制方程进行了离散，进一步提高了模型计算的精确性。
[0086]
(3)本发明的基于物理中性面的功能梯度复合材料无网格sph分析模型通过与文献解和自编程有限元程序的比较，验证了本文模型的正确性。
附图说明
[0087]
为了更清楚地说明本发明实施例中的技术方案，下面将对实施例或现有技术描述中所需要使用的附图作简单地介绍，显而易见地，下面描述中的附图仅仅是本发明的一些实施例，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据这些附图获得其它的附图。
[0088]
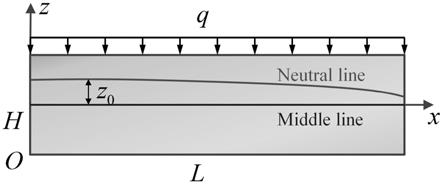
图1为本发明一实施例提供的基于物理中性面的功能梯度复合材料无网格sph分析模型的双向功能梯度梁示意图。
具体实施方式
[0089]
为了使本发明所要解决的技术问题、技术方案及有益效果更加清楚明白，以下结合附图及实施例，对本发明进行进一步详细说明。应当理解，此处所描述的具体实施例仅用以解释本发明，并不用于限定本发明。
[0090]
需要说明的是，当部件被称为“固定于”或“设置于”另一个部件，它可以直接或者间接位于该另一个部件上。当一个部件被称为“连接于”另一个部件，它可以是直接或者间
接连接至该另一个部件上。术语“上”、“下”、“左”、“右”、“前”、“后”、“竖直”、“水平”、“顶”、“底”、“内”、“外”等指示的方位或位置为基于附图所示的方位或位置，仅是为了便于描述，不能理解为对本技术方案的限制。术语“第一”、“第二”仅用于便于描述目的，而不能理解为指示或暗示相对重要性或者隐含指明技术特征的数量。“多个”的含义是两个或两个以上，除非另有明确具体的限定。
[0091]
步骤(1)，建立一维ssph公式
[0092]
对于具有连续导数到(n+1)阶的函数u(x)，通过泰勒级数展开，利用函数值及其在邻近点x
i
上的导数逼近函数在x
j
上的值，
[0093][0094]
忽略四阶以上的项，式(1)可以写成矩阵形式为
[0095]
u(x)＝a(x
i
,x
j
)q(x
i
)
ꢀꢀꢀ
(1)
[0096]
其中，
[0097][0098]
a(x
i
,x
j
)＝[1,x
j-x
i
,(x
j-x
i
)2,(x
j-x
i
)3,(x
j-x
i
)4]
[0099]
作为向量q(x
i
)的元素，函数u的核估计及其在x处的导数是由式(1)得到的未知量，为此，将式(1)两边同时乘以w(x
i
,x
j
)a(x
i
,x
j
)
t
，得到
[0100][0101]
式中w(x
i
,x
j
)为核函数，确定该点的紧支域；x
i
到x
j
的距离越小，核函数的值越大；
[0102]
使用最广泛的三次b样条函数，
[0103][0104]
其中h定义为平滑长度或核长度，s＝|x
j-x
i
|/h；
[0105]
对在x
i
的支持域中的每个相邻粒子x
j
，计算式(2)，并对公示的两边求和，得到
[0106][0107]
其中，n
i
为在x
i
的支持域中的临近粒子x
j
的个数；
[0108]
由式(3)，可计算出向量q
[0109][0110]
其中，
[0111][0112]
最后，通过式(4)中向量q中的5个元素，使用缩写形式，可以估计出函数及其一阶到四阶的推导
[0113][0114]
步骤(2)，考虑长度为l、厚度为h的矩形功能梯度复合材料梁(fgb)，承受横向均布力q，如附图1所示。双向fgb的材料性能沿x(长度)和z(厚度)方向连续变化，服从幂律函数。考虑了由两种和四种不同材料组成的双向fgb。
[0115]
第一种情况，梁由陶瓷和金属组成，有效材料特性p随厚度和长度的变化而变化，
[0116][0117]
式中，n
x
和n
z
分别为材料性能随梁长和梁厚变化的梯度指数；
[0118]
第二种情况，假设梁由陶瓷1、陶瓷2和金属1、金属2组成，其体积分数v在轴向和横向上的变化如下:
[0119][0120]
其中，下标c1、c2、m1和m2分别表示组成成分:陶瓷1、陶瓷2、金属1和金属2；
[0121]
梁的材料特性p可以用voigt模型表示为
[0122]
p＝p
c1
v
c1
+p
c2
v
c2
+p
m1
v
m1
+p
m2
v
m2
[0123]
其中p
c1
、p
c2
、p
m1
、p
m2
分别为陶瓷1、陶瓷2、金属1、金属2的性能；得到材料的杨氏模量e、剪切模量g性质，如下:
[0124][0125]
其缩写形式为：
[0126]
基于rbt的sph实施，构建双向梁的平衡方程，然后用ssph公式来表示，这里考虑由四种不同材料组成的梁。
[0127]
具体地，基于rbt，梁任意点的轴向位移和横向位移可表示
[0128]
w(x,z)＝w0(x)
[0129]
其中u、w分别表示沿x、z方向的位移，w0为梁中间表面点的横向变形，φ(x)为横截面的旋转，α＝4/3h2；
[0130]
由于杨氏模量在厚度方向和长度方向同时变化，中间面与中性面不重合，公式(5)不能准确描述双向fgb的挠度行为；因此，应将物理中性面与rbt相结合，则位移场可表示为
[0131][0132]
w(x,z)＝w0(x)
[0133]
参数z0，c2定义为
[0134][0135]
z0为物理中性面与中间面之间的距离，将式(6)代入式(7)，得到:
[0136][0137][0138]
显然，对于均质的或是仅在x方向连续变化的或常规fgb，由于n
z
为零，物理中性面与中间面重合；
[0139]
由动力学方程可得轴向线性应变和剪切应变:
[0140][0141]
其中，β＝3α＝4/h2。
[0142]
进一步地，所述控制方程建立过程为：
[0143]
用轴向应力和轴向应变表示的梁的虚拟应变能δu可以表示为
[0144][0145]
其中δ为变分算子，a为梁的横截面面积，σ
xx
为正应力，σ
xz
为横向剪应力；应用胡克定律，可以计算出应力，
[0146][0147]
将公式(6),(8)和(10)带入式(9)，可得
[0148][0149]
其中，
[0150][0151]
横向荷载q的虚势能为
[0152][0153]
应用虚位移原理δw＝δu+δv＝0，得到
[0154][0155]
因此，可以得到平衡方程
[0156][0157]
将式(11)代入式(12)，四种材料的fgb的rbt控制方程可以表示为
[0158][0159][0160]
其中包括如下定义，
[0161][0162][0163][0164][0165]
进一步地，所述离散化过程为：
[0166]
利用式(5)中函数及其一阶至四阶导数的ssph表示，四种不同材料构成的双向fgb
的平衡方程可离散为如下两式，
[0167][0168][0169][0170]
值得一提的是在数值应用过程中，针对fgb弯曲变形中中性面与中间面不重合的问题，用sph梁模型进行了几个数值算例的求解，梁由两种或四种不同的材料组成，材料性能在两个方向上呈平滑，服从幂律函数，研究了粒子离散化、幂指数和边界条件对梁挠度的影响。
[0171]
最后，验证该分析模型的正确性，具体地，在两种材料组成的fgb厚梁的测试中，首先测试了所提出的sph梁模型的收敛性能。梁长l＝1000mm，厚度h＝200mm。梁顶面施加均布荷载q＝0.1n/mm2，两端简支。由陶瓷和铝两种不同材料制成的结构，具有以下材料性能：
[0172]
陶瓷(al2o3):e
c
＝380gpa，ν
c
＝0.3；
[0173]
金属(铝):e
m
＝70gpa，ν
m
＝0.3
[0174]
根据式材料特性p的计算公式，双向fgb的有效材料特性在长度和厚度方向上有所不同。利用全拉格朗日修正光滑粒子法(cspm)建立的二维实体模型进行了动态求解。为了便于比较，采用带阻尼的tl cspm实体模型的准静态解作为参考，该方法比有限元结果更准确、更稳定。
[0175]
首先，考虑了新提出的ssph梁模型的收敛性能。为此，将区域离散为7、9、11、15、21、41和101个sph粒子，粒子间平均距离分别为167、125、100、71、25和10mm。梯度指数n
x
和n
z
均固定为5，核长度与粒子距离的比值设为2。梁的静态横向挠度可由提出的ssph梁模型计算，不同粒子分布下得到的无量纲最大挠度以及采用100
×
20点的tl cspm实体模型得到的准静态结果，如表1所示。
[0176]
表1不同粒子分布下fgb的无量纲最大挠度
[0177][0178]
从表1可以清楚地看到，随着粒子数的增加，预测的挠度会逐渐接近参考值，然后趋于稳定。当数字为7时，误差最大，为3.6％。在后面的计算中，采用11个分散在梁中线的sph粒子，其误差小于2.5％。
[0179]
梯度指数n
x
和n
z
的取值范围为[0,0.5,1,2,5]。当两者都为零时，梁是均匀的，而当其中一个为零时，梁则变成单向fgb。最大无量纲挠度列于表2，并与tl cspm获得的参考值进行比较。
[0180]
表2不同梯度指数下fgb的最大无量纲挠度
[0181][0182]
由表2可以很明显地看出，由现有sph梁模型计算得到的静态解与参考结果吻合较好，显示了该方法具有较好的求解能力。当材料均质且仅由高刚度陶瓷组成时，变形最小。随着梯度指数的增大，由于fgb中金属含量的增加，其挠度增大。
[0183]
具体地，在四种材料组成的fgb厚梁的测试中，两端是简单支撑，压力加载在顶部边缘。梁的长度为l＝1000mm，厚度为h＝50mm。双向fgms由两种陶瓷和两种金属制成，其杨氏模量为，
[0184]
陶瓷1(zno2):e
c1
＝200gpa；陶瓷2(al2o3):e
c2
＝390gpa；
[0185]
金属1(ti):e
m1
＝105gpa；金属2(fe):e
m2
＝206gpa.
[0186]
这四种材料的泊松比均为0.3，长度方向和厚度方向的梯度指数均设置为[0,0.5,1,2,5]。为验证其准确性，采用1000
×
50四边形单元的细网格，通过自编程的有限元二维实体代码在matlab中对该类型双向fgb进行了有限元分析。得到的横向最大无量纲挠度见表3。
[0187]
表3不同梯度指数下s-s型fgb的横向最大无量纲挠度
[0188][0189]
从表中，显而易见，现有的ssph梁模型和有限元实体模型得到的静态梁挠度基本吻合，最大误差小于1.8％，表明该方法在四种不同材料组成的fgb弯曲分析中具有良好的性能。
[0190]
然后，考虑了边界条件对梁变形的影响。使用所提出的sph方法分析了夹紧简支(c-s)和夹紧夹紧(c-c)fgbs，结果列于表4和表5，同时给出应用有限元方法得到的结果。
[0191]
表4不同梯度指数下c-s fgb的无量纲挠度
[0192][0193][0194]
表5不同梯度指数下c-c fgb的无量纲挠度
[0195][0196]
从表4和表5中，可以看出ssph方法和有限元方法分析的结果保持一致。随着两个方向梯度指数的增大，横向变形增大。在相同的梯度条件下，s-s梁的横向挠度最大，c-c梁
最小，因为在夹紧梁中设置了更多的固定自由度。
[0197]
值得一提的是，本实施例基于reddy-bickford梁理论的三阶剪切变形理论，建立了用于双向功能梯度梁弯曲分析的对称光滑粒子流体动力学(ssph)方法。考虑到了由于材料的性能在纵向和横向均平稳连续地变化而产生的的物理中性线和几何中线的非重合性。推导了包含物理中性面概念和不同材料性质的控制方程，并用ssph方法表示。首先通过使用不同的粒子分布验证了该模型的收敛性能。研究了由两种或四种不同材料组成的fgbs的变形行为，并与文献和有限元分析结果进行了比较，验证了计算结果的准确性。随着梯度指数的增大，金属含量的增加，挠度随之增大。综上所述，所提出的ssph模型可以精确地求解由两种或四种不同材料构成的双向fgb的弯曲行为。
[0198]
以上仅为本发明的较佳实施例而已，并不用以限制本发明，凡在本发明的精神和原则之内所作的任何修改、等同替换和改进等，均应包含在本发明的保护范围之内。