一种非线性系统反演的快速收敛方法与流程

[0001]
本发明涉及一种非线性系统反演的快速收敛方法，属于基于神经网络方法的系统反演技术领域。


背景技术：

[0002]
因果关系是工程和科学问题中的一个重要规则。对于同一个系统，不同的原因将可能导致不同的结果。当已知某个问题的原因时，推导问题的结果，该过程被称为正问题。在数学的表述中，就是如果已知某个问题的数学模型，那么根据输入，就可以计算出系统的输出。反过来，如果已知某个问题的结果，据此出发反推问题的成因，则该问题被称为反问题，或者反演问题。用数学的方法表述就是，如果知道模型的输出和输入，求模型的参数或者规则，则该问题称为反演问题。在线性和非线性系统中，如果需要反演的是系统的参数，或者系统的模型，则该问题被称为系统反演。
[0003]
系统反演的定义是，在已知输入和输出的前提下，在规定的一系列系统模型集合中，挑选出最合适的一个系统，该系统能够等价地表示原系统的行为，则该系统可以作为原系统的一个反演结果。由此可见，反演结果并不是唯一的。只要反演得出的系统的行为与原系统等价，则这些系统都可以作为原系统的反演结果。例如，可以用有限冲激响应系统反演有限冲激响应系统，也可以用有限冲激响应系统反演无限冲激响应系统。根据线性系统的理论，只要系统阶数足够高，那么就可以用一个类型的系统完全地等价代替另一个系统。反之亦然，即用无限冲激响应系统等价地反演有限冲激响应系统，也是可以的。
[0004]
系统反演方法一般而言可以分为两大类，一类是线性系统反演方法，另一类是非线性系统反演方法。线性系统反演方法模型简单，计算快速，在20世纪80年代已经发展趋于成熟。典型代表有最小二乘反演方法、最大似然反演方法和梯度下降反演法。这些理论和方法已经得到了广泛的应用，并在工程实践中经过了多次的检验。
[0005]
然而，在现实情况中，非线性往往普遍存在。线性通常只是非线性在某些条件下的近似。因而非线性系统反演方法的研究更具有实用价值。但是，由于非线性系统种类众多，理论复杂，找不到统一的设计模式，所以非线性系统反演方法仍然是领域内的研究重点。
[0006]
非线性系统反演方法主要包括volterra级数分解法，narmax模型子集法，h
∞
控制理论，扩展卡尔曼滤波算法，微分几何法和神经网络方法。其中，神经网络方法由于具有强大的非线性表达能力，并且结构灵活，所以近年受到广泛的关注。实际上，理论上只要有足够多的数据、足够多数量的神经元和足够多的层数，神经网络方法可以表描述任意复杂的线性和非线性系统。所以，神经网络反演方法在近年受到巨大的关注。
[0007]
神经网络反演方法中，神经网络的初始化过程对最终的反演效果起着至关重要的影响。神经网络在训练结束时，将收敛于某一最优或者次优解。由于现有的成熟可用的寻优方法，如梯度下降法等，只能保证寻找到局部最优解，无法保证得到全局最优解，所以如何保证得到全局最优解是神经网络反演方法的关注重点。


技术实现要素：

[0008]
针对上述现有技术，本发明要解决的技术问题是提供一种可以使得神经网络具有更快的收敛速度以及尽可能地收敛于全局最优解的非线性系统反演的快速收敛方法。
[0009]
为解决上述技术问题，本发明的一种非线性系统反演的快速收敛方法，包括以下步骤：
[0010]
步骤1：获得非线性系统的输入和输出；
[0011]
步骤2：把系统看作线性系统，使用最小二乘反演算法实现系统反演，得到系统的单位冲激响应，对单位冲激响应进行累加，得到系统的单位阶跃响应；
[0012]
步骤3：将单位冲激信号作为神经网络的输入，单位冲激响应作为神经网络的输出，制作数据集1；
[0013]
步骤4：将单位阶跃信号作为神经网络的输入，单位阶跃响应作为神经网络的输出，制作数据集2；
[0014]
步骤5：合并数据集1和数据集2，得到合并后的数据集。然后在合并后的数据集中添加随机噪声，添加10次随机噪声，将数据的数量扩充10倍，形成扩充后的数据集；
[0015]
步骤6：打乱数据集中样本排列的顺序；
[0016]
步骤7：划分数据集，具体做法是将数据集前80％数量的样本作为训练集，余下样本作为验证集；
[0017]
步骤8：预训练：使用训练集训练神经网络，然后使用验证集进行验证，同时记录验证集的代价函数，然后保存此代价函数对应的神经网络的权重，随着训练次数的进行，代价函数会逐渐下降，此时神经网络正在接近某一局部或者全局最优值，但当训练次数超过某一数值时，代价函数便逐渐上升，此时便出现了过拟合现象，将代价函数有降转成升的地方，称为拐点；
[0018]
步骤9：做出代价函数的变化曲线，观察代价函数曲线是否出现拐点，即是否随着训练次数的增加而上升，若出现拐点，则停止训练，否则执行步骤8；
[0019]
步骤10：读取拐点处保存的权重，作为神经网络的初始化数值，在此基础上，开始正式的训练；
[0020]
步骤11：结束。
[0021]
本发明的有益效果：本发明提出了一种非线性系统反演的快速收敛方法。该方法充分利用了线性系统反演的成熟理论和方法，将其结论用于辅助非线性系统反演，尽可能找到最优值。本发明提出，利用最小二乘线性系统反演结果初始化神经网络反演方法的参数初始值，可以使得神经网络拥有更快的收敛速度，以及尽可能地收敛于全局最优值。
附图说明
[0022]
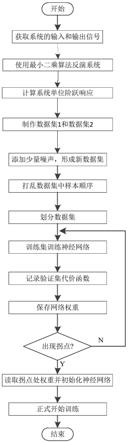
图1为本发明的执行流程图。
具体实施方式
[0023]
下面结合附图对本发明具体实施方式做进一步说明。
[0024]
神经网络具有强大的非线性表达能力，因而可以用于线性和非线性系统的反演任务中。考虑到实际系统往往非常复杂，无法保证目标函数是凸函数，也无法保证特定问题的
神经网络求解方法是凸优化问题，所以神经网络方法的一个重要问题就是如何找到全局最优解。但是，现有的工程中常用的神经网络寻优方法，如梯度下降法等，往往无法保证神经网络收敛于全局最优解。所以，本发明提供了一种方法，借助于线性系统反演的成熟理论，使得神经网络更快地收敛，同时尽可能地收敛于全局最优解。
[0025]
线性系统反演理论在20世纪80年代便已发展成熟。这是因为线性系统模型简单可靠，因而对线性系统反演问题的讨论可以使用常规数学工具较为简单地完成。因此，线性系统的反演方法已经趋于完善。当待反演系统为非线性系统时，线性系统反演方法往往无法得到问题的真正解。这是因为非线性模型可以无误差地描述线性系统，而线性系统无法对非线性系统进行无误差地描述，只能在一定误差范围内，对非线性系统进行尽可能地近似。
[0026]
但是，使用线性系统反演方法对非线性系统进行反演的工作也是有意义的。这是因为，非线性系统反演方法往往非常复杂，而且存在多个局部最优解。此时非线性系统的反演性能很大程度上依赖于算法的参数选择，如初始化参数的设置。如果初始化参数设置于某一局部最优值附近，则非线性系统反演算法很可能最终收敛于该局部最优值，而非全局最优值。
[0027]
为解决局部最优值的问题，现在已经存在了多种方法，如带冲量的梯度下降算法。该算法在梯度下降算法的基础上添加了一个冲量，借助该冲量，梯度下降算法可以跨过较窄的局部最优值，从而一定程度上缓解了收敛于局部最优的问题。但是，这些算法只属于工程的创新，无法从数学上保证算法收敛于全局最优。而且，这些算法也依赖于优化问题初始值的设置。若初始值设置不当，即使使用带冲量的梯度下降算法，也可能使得问题最终收敛于初始值附近的局部最优值。
[0028]
因此，在当前的求解算法中，如何设置神经网络的初始值成为提高非线性系统反演性能的关键。考虑到线性反演算法理论成熟，数学完备，能够从数学上得到线性反演问题的全局最优解，所以可以借助线性反演算法提高非线性反演算法的性能。
[0029]
对于非线性反演问题，可以先将其视作线性反演问题，然后就可以使用线性反演算法求得问题的解。线性反演算法可以求得线性系统反演的全局最优解，无法求得非线性系统反演的全局最优解。但线性反演算法计算速度快，反演精度高，同时具有较为完备的数学理论支持，所以可以用于反演非线性系统。此时线性系统得到的解为近似解。
[0030]
当使用基于最小二乘的反演算法时，目标函数为反演系统的输出误差平方和。算法通过最小化该系统的输出误差平方和求得问题的全局最优解。当待反演系统为非线性系统时，目标函数仍旧为模型的输出与系统输出误差的平方和。此时，算法在寻找一个最优的线性系统，让这个线性系统尽可能地接近非线性系统，并使二者的误差尽可能地小，即使二者尽可能地接近。所以，可以认为，使用基于最小二乘的反演算法得到的解，已经尽可能地接近全局最优解。最小二乘反演算法得到的解处于非线性反演问题的全局最优解附近。
[0031]
因此，在获得全局最优解附近的一个初始数值后，若使得非线性反演算法以此为出发点，寻找问题的最优解，则可能使得非线性反演问题最终收敛于全局最优解。
[0032]
具体做法是，在利用最小二乘反演算法获得问题的解以后，该解便是系统的单位冲激响应。所以，以单位冲激作为输入信号，同时以最小二乘反演算法的解作为输出，可以对神经网络进行训练。为了尽可能扩大训练样本，可以对单位冲激响应进行积分(连续形式)或者累加运算(离散形式)，得到系统的单位阶跃响应。单位阶跃信号和单位阶跃响应也
可以作为神经网络的训练集。
[0033]
在训练过程中，由于神经网络参数众多，而数据有限，所以需要使用数据增强技术，扩充训练样本。一个常用的做法是，在输入和输出信号中添加少量随机噪声，于是可以得到大量不同的训练样本。这些训练样本可以一定程度上解决训练样本不足的问题。但该方法也不能完全解决训练样本数量不足的问题，所以使用该方法扩充训练集时，将训练集数量扩充3-10倍即可。这是因为，根本而言，这种方法只是扩充了训练集的数量，而没有丰富训练集中包含的类型，所以使用该方法无限制地扩充样本是无意义的。
[0034]
至此，可以使用扩充后的训练集对神经网络进行训练。将数据划分为训练集和验证集，在每次训练完成后，都要使用验证集验证训练效果。训练效果可以用代价函数的数值作为表征。验证集上的代价函数拥有较大数值时，说明训练效果不好，神经网络没有收敛于最优值。当验证集上的代价函数数值较小时，说明训练效果好，神经网络收敛于最优值。
[0035]
随着训练的进行，需要记录每次训练完成后神经网络中各变量的具体数值，并对其进行编号，以便根据训练次数找到这些变量并再次使用。这是因为，由于输入样本较少，随着训练的进行，神经网络必将出现过拟合现象。过拟合出现时，神经网络在训练集上的代价函数可以取得较小的数值，甚至可以为0，但是在训练集上的代价函数将拥有较大的数值。根据此特点，可以找到神经网络发生过拟合之前的网络中参数具体数值，这些数值便可以作为神经网络的初始化值，然后进行正式的训练。此时神经网络已经处于全局最优值附近，若再配合基于冲量的梯度下降寻优算法，则神经网络将很可能收敛于全局最优值。另一方面，由于此时神经网络已经处于全局最优值附近，所以在后续的训练过程中，神经网络也将获得较快的收敛速度。
[0036]
结合图1，本发明包括以下步骤：
[0037]
步骤1：获得非线性系统的输入和输出。
[0038]
步骤2：把系统看作线性系统，使用最小二乘反演算法实现系统反演，得到系统的单位冲激响应。对此单位冲激响应进行累加，得到系统的单位阶跃响应。
[0039]
步骤3：将单位冲激信号作为神经网络的输入，单位冲激响应作为神经网络的输出，制作数据集1。
[0040]
步骤4：将单位阶跃信号作为神经网络的输入，单位阶跃响应作为神经网络的输出，制作数据集2。
[0041]
步骤5：合并数据集1和数据集2，得到合并后的数据集。然后在合并后的数据集中添加少量的随机噪声，形成新的数据集。添加10次随机噪声，将数据的数量扩充10倍，形成扩充后的数据集，在步骤6-步骤11中，将此扩充后的数据集称为数据集。
[0042]
步骤6：打乱数据集中样本排列的顺序。
[0043]
步骤7：划分数据集，具体做法是将数据集前80％数量的样本作为训练集，余下样本作为验证集。
[0044]
步骤8：预训练：使用训练集训练神经网络，然后使用验证集进行验证。同时记录验证集的代价函数，然后保存此代价函数对应的神经网络的权重。随着训练次数的进行，代价函数会逐渐下降，此时神经网络正在接近某一局部或者全局最优值。但当训练次数超过某一数值时，代价函数便逐渐上升，此时便出现了过拟合现象。将代价函数有降转成升的地方，称为拐点。
[0045]
步骤9：做出代价函数的变化曲线。观察代价函数曲线是否出现拐点，即是否随着训练次数的增加而上升。若出现拐点，则停止训练，否则执行步骤8。
[0046]
步骤10：读取拐点处保存的权重，作为神经网络的初始化数值，在此基础上，开始正式的训练。此时神经网络在全局最优值附近，所以很可能收敛于全局最优，并且收敛速度较快。
[0047]
步骤11：结束。