基于Spark的分布式改进差分进化算法的电源规划方法与流程

基于spark的分布式改进差分进化算法的电源规划方法
技术领域
[0001]
本发明涉及电源规划领域，尤其涉及一种一种基于spark计算引擎的分布式改进差分进化算法进行分布式电源规划方法。


背景技术：

[0002]
分布式发电和大电网结合是电力系统的发展趋势之一，二者可以相互取长补短。分布式发电具有发电方式灵活、投资省以及提高电能质量等优点。但是当分布式电源直接接入电网后，会对电网产生很大的影响，包括电压水平、网损、可靠性、灵活性等方面，其影响的大小与分布式电源的安装位置和容量直接相关。甚至不合理的分布式电源接入会使得电网的安全稳定运行受到严重威胁。因此，对分布式电源的选址和定容研究就显得尤为关键。近年来，对分布式电源选址和定容的研究已经成为了国内外研究的热点。但是这些研究存在采用的算法收敛速度慢，易陷入局部最优解的缺陷，因此基于以上的不足本发明提出了一种基于spark计算引擎的改进分布式差分进化算法。建立以分布式电源建设和运行总费用最小为优化子目标的规划模型，并且在14节点配电网测试系统进行分布式电源选址和定容。
[0003]
差分进化算法作为一种启发式算法，在搜索速度方面存在固有缺陷，不能在大规模优化问题上应用。为了有效提高传统差分进化算法的搜索效率，本文提出一种分布式的改进差分进化算法(distributed improved differential evolution，dide)，对传统差分进化算法进行改进，使其适应spark分布式计算框架的特点，从而充分利用分布式集群的计算资源，提高算法的搜索效果。


技术实现要素：

[0004]
本发明的目的是提供一种基于spark的分布式改进差分进化算法的电源规划方法，用于解决现有技术对分布式电源选址和定容存在收敛速度慢，易陷入局部最优解等缺陷。
[0005]
本发明采用以下技术方案：一种基于spark的分布式改进差分进化算法的电源规划方法，包括种群计算和种群汇总，其中种群计算包括以下步骤：
[0006]
step1：进行参数初始化；
[0007]
step2：根据全局或局部搜索阶段，对差分进化进行不同的随机初始化；
[0008]
step3：随机选取3个不与当前个体重复的个体进行种群更新；
[0009]
step4：针对新旧种群对应个体的每一个维度进行交换；
[0010]
step5:计算分布式电源的建设和运行总费用，并且将该值作为dide的适应度值；
[0011]
step6:根据电力系统潮流计算约束条件筛选符合约束的个体，如果个体不符合潮流计算的约束条件则将个体适应度调整为最大值；
[0012]
step7：更新个体历史最优值；
[0013]
step8：更新种群历史最优值。
[0014]
在本发明一实施例中，在参数初始化阶段，对分布式计算的并行度p进行设置，并行度的作用是要按照数据数量的上下界将其分割为p组数据，每组数据生成spark的一个rdd，代表一个例子种群，之后在各rdd中分别对各个种群进行计算。
[0015]
在本发明一实施例中，全局搜索的种群随机初始化步骤中使用公式如下：
[0016]
x
i
＝rand*(ub-lb)+lb where i
←
(1：n)
ꢀꢀꢀ
(1)
[0017]
其中，x
i
为粒子第i个个体的位置，
[0018]
lb和ub为粒子位置x
i
的上下界，
[0019]
rand为(0，1)的平均随机数，
[0020]
n种群中个体数量。
[0021]
在本发明一实施例中，局部搜索的种群随机初始化步骤中使用公式如下：
[0022][0023]
其中，x
i
为粒子第i个维度的位置，
[0024]
β为搜索到的已知最优适应度，
[0025]
gaussian_rand为均值为0，方差为1的高斯分布随机数，
[0026]
为搜索到的已知最优个体，
[0027]
n种群中个体数量。
[0028]
进一步的，全局搜索阶段占总计算时间的20％，不限制种群计算的更新次数。局部搜索阶段占总计算时间的80％；若局部搜索阶段的最优值连续n次没有更新，则令局部搜索阶段的最大更新次数在原有基础上加2。
[0029]
在本发明一实施例中，step3包括以下具体步骤：随机选取3个不与当前个体重复的个体分别为x
r1
，x
r2
与x
r3
，按以下公式进行种群位置更新：
[0030][0031][0032]
其中，t为种群计算的当前迭代次数，
[0033]
i为预设的最大迭代次数，
[0034]
为个体i在t代的位置，
[0035]
m等于0.5。
[0036]
在本发明一实施例中，step4：针对新旧种群对应个体的每一个维度按照以下概率进行交换：
[0037]
p＝c/d
ꢀꢀꢀ
(5)
[0038]
其中，
[0039]
c等于0.9，
[0040]
d为个体的维度值。
[0041]
在本发明一实施例中，step5中分布式电源的建设和运行总费用计算函数为：
[0042][0043]
式中：t
max
是分布式电源的最大发电小时数；m为配电网中的分布式电源总个数；s
dgi
为第i个分布式电源额定容量；c
edgi
为第i个分布式电源的单位电量成本；η
i
为第i个分布
式电源的功率因数；c
dg1i
为第i个分布式电源的安装成本；c
dg2i
为第i个分布式电源的运行维护费用成本；c
dg3i
为第i个分布式电源的发电燃料费用成本。
[0044]
在本发明一实施例中，step6中潮流计算约束条件包括等式和不等式约束条件，其中，等式约束条件为有功功率平衡方程:
[0045][0046]
式中：p
dgi
为节点i的分布式电源有功；p
gi
为节点i处发电机发出的有功；p
l
为有功网损；p
d
为系统有功负荷。
[0047]
在本发明一实施例中，不等式约束条件包括:
[0048]
节点电压上下限约束：|v
i
|
min
≤v
i
≤|v
i
|
max
ꢀꢀꢀ
(8)
[0049]
支路电流约束：|i
i
|≤|i
i
|
max
ꢀꢀꢀ
(9)
[0050]
分布式电源容量约束:
[0051][0052]
式中:和分别表示安装在节点i处的分布式电源容量下限和上限；p
ldi
为节点i上负荷有功；η为分布式电源有功总量占系统有功总量的最大比例；n
dg
为分布式电源安装总数；n为节点数；|v
i
|
min
和|v
i
|
max
分别表示节点i处电压最小值和最大值；|i
i
|和|i
i
|
max
分别为第i条支路电流大小和允许通过的电流最大值。
[0053]
在本发明一实施例中，step7包括以下步骤：如果种群中的个体适应度小于个体历史最优适应度，则将当前个体作为历史最优个体，当前个体适应度作为历史最优个体适应度。
[0054]
在本发明一实施例中，step8包括以下步骤：如果种群中的个体适应度小于种群历史最优适应度，则更新当前个体作为种群历史最优个体，当前个体的适应度为种群历史最优个体适应度。
[0055]
在本发明一实施例中，在总体层面上，各rdd完成各自种群的迭代计算之后，需要进行各种群间的信息交互，即找出全部种群上一次迭代计算时产生结果中的最优解；如果该解比当前全部种群的最优解还好，则更新当前最优解，并且将最优解继续传递到下一次的各个种群的迭代计算中。
[0056]
本发明的分布式电源规划方法充分利用分布式集群的计算资源，提高算法的搜索效果；以分布式电源建设和运行总费用最小为优化子目标的规划模型，实现配电网测试系统进行分布式电源最优规划。
附图说明
[0057]
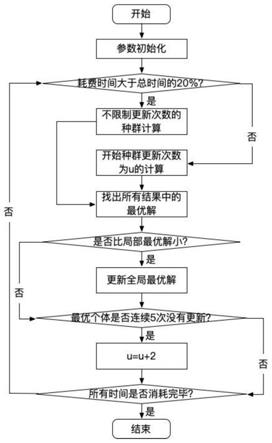
图1为本发明种群计算流程图。
[0058]
图2为发明种群汇总信息交互流程图。
[0059]
图3为本发明一实施例14节点辐射型配电系统示意图。
具体实施方式
[0060]
为使本发明实施例的目的、技术方案和优点更加清楚，下面将结合本发明实例的
附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。
[0061]
对分布式电源选址和定容的研究已经成为了国内外研究的热点。但是这些研究存在采用的算法收敛速度慢，易陷入局部最优解的缺陷，因此基于以上的不足本发明采用一种基于spark计算引擎的改进分布式差分进化算法，建立以分布式电源建设和运行总费用最小为优化子目标的规划模型，并且在14节点配电网测试系统进行分布式电源选址和定容。
[0062]
本发明采用以下技术方案：一种基于spark的分布式改进差分进化算法的电源规划方法，包括种群计算和种群汇总，其中种群计算包括以下步骤：
[0063]
step1：进行参数初始化；
[0064]
step2：根据全局或局部搜索阶段，对差分进化进行不同的随机初始化；
[0065]
step3：随机选取3个不与当前个体重复的个体进行种群更新；
[0066]
step4：针对新旧种群对应个体的每一个维度进行交换；
[0067]
step5:计算分布式电源的建设和运行总费用，并且将该值作为dide的适应度值；
[0068]
step6:根据电力系统潮流计算约束条件筛选符合约束的个体，如果个体不符合潮流计算的约束条件则将个体适应度调整为最大值；
[0069]
step7：更新个体历史最优值；
[0070]
step8：更新种群历史最优值。
[0071]
在参数初始化阶段，需要对分布式计算的并行度p进行设置，并行度的作用是要按照数据数量的上下界将其分割为p组数据，每组数据生成spark的一个rdd，代表一个例子种群，之后在各rdd中分别对各个种群进行计算。
[0072]
在分布式电源规划中，将dide算法中个体的维度设置为n＝14维，每个维度中的值为自然数，代表在电网中该节点的电源安装台数。
[0073]
种群计算是算法对解空间进行具体的搜索的过程，在spark中是不可分割的最小计算步骤。
[0074]
较佳的，可以将每次计算的迭代次数设置为“总迭代次数*0.8/p/5”。
[0075]
在本发明一实施例中，种群大小为10。
[0076]
以下详细阐述种群计算流程和步骤。具体步骤及流程图如图1所示。
[0077]
step1：进行参数初始化；
[0078]
step2：根据全局或局部搜索阶段，对差分进化进行不同的随机初始化。
[0079]
较佳的，全局搜索的种群随机初始化步骤中使用公式如下：
[0080]
x
i
＝rand*(ub-lb)+lb where i
←
(1：n)
ꢀꢀꢀ
(1)
[0081]
其中,
[0082]
x
i
为粒子第i个个体的位置，
[0083]
lb和ub为粒子位置x
i
的上下界，
[0084]
rand为(0,1)的平均随机数，
[0085]
n种群中个体数量。
[0086]
局部搜索阶段占总计算时间的80％。
[0087]
较佳的，局部搜索的种群随机初始化步骤中使用公式如下：
[0088][0089]
其中,
[0090]
x
i
为粒子第i个维度的位置，
[0091]
β为搜索到的已知最优适应度，
[0092]
gaussian_rand为均值为0，方差为1的高斯分布随机数，
[0093]
为搜索到的已知最优个体，
[0094]
n种群中个体数量。
[0095]
step3：随机选取3个不与当前个体重复的个体分别为x
r1
,x
r2
与x
r3
：
[0096][0097][0098]
其中，
[0099]
t为种群计算的当前迭代次数，
[0100]
i为预设的最大迭代次数，
[0101]
为个体i在t代的位置，
[0102]
m等于0.5。
[0103]
step4：针对新旧种群对应个体的每一个维度按照以下概率进行交换。
[0104]
p＝c/d
ꢀꢀꢀ
(5)
[0105]
其中，
[0106]
c等于0.9，
[0107]
d为个体的维度值。
[0108]
step5：计算分布式电源的建设和运行总费用，并且将该值作为dide的适应度值。
[0109]
在本发明一实施例中，分布式电源的建设和运行总费用计算函数为：
[0110][0111]
式中:t
max
是分布式电源的最大发电小时数；m为配电网中的分布式电源总个数；s
dgi
为第i个分布式电源额定容量；c
edgi
为第i个分布式电源的单位电量成本；η
i
为第i个分布式电源的功率因数；c
dg1i
为第i个分布式电源的安装成本；c
dg2i
为第i个分布式电源的运行维护费用成本；c
dg3i
为第i个分布式电源的发电燃料费用成本。
[0112]
step6:个体筛选。根据电力系统潮流计算约束条件筛选符合约束的个体。
[0113]
如果个体不符合潮流计算的约束条件则将个体适应度调整为最大值。
[0114]
在本发明一实施例中，潮流计算约束条件包括等式和不等式约束条件。
[0115]
其中，等式约束条件为有功功率平衡方程:
[0116][0117]
式中:p
dgi
为节点i的分布式电源有功；
[0118]
p
gi
为节点i处发电机发出的有功；
[0119]
p
l
为有功网损；p
d
为系统有功负荷。
[0120]
其中，不等式约束条件包括:
[0121]
节点电压上下限约束：
[0122]
|v
i
|
min
≤v
i
≤|v
i
|
max
ꢀꢀꢀ
(8)
[0123]
支路电流约束:
[0124]
|i
i
|≤|i
i
|
max
ꢀꢀꢀ
(9)
[0125]
分布式电源容量约束:
[0126][0127]
式中:和分别表示安装在节点i处的分布式电源容量下限和上限；p
ld i
为节点i上负荷有功；η为分布式电源有功总量占系统有功总量的最大比例；n
dg
为分布式电源安装总数；n为节点数；|v
i
|
min
和|v
i
|
max
分别表示节点i处电压最小值和最大值；|i
i
|和|i
i
|
max
分别为第i条支路电流大小和允许通过的电流最大值。
[0128]
step7：更新个体历史最优值。
[0129]
如果种群中的个体适应度小于个体历史最优适应度，则将当前个体作为历史最优个体，当前个体适应度作为历史最优个体适应度。
[0130]
step8：更新种群历史最优值。
[0131]
如果种群中的个体适应度小于种群历史最优适应度，则更新当前个体作为种群历史最优个体，当前个体的适应度为种群历史最优个体适应度。
[0132]
种群汇总：在总体层面上，算法分为全局搜索和局部搜索两个阶段。全局搜索阶段占总计算时间的20％，不限制种群计算的更新次数。局部搜索阶段占总计算时间的80％。
[0133]
总体层面的流程示意图参见图2。
[0134]
在本发明一较佳实施例中，若最优值连续n次没有更新，则令局部搜索阶段的最大更新次数u在原有基础上加2。
[0135]
在本发明一具体实施例中，局部搜索阶段的最大更新次数u的初始值设置为15，n为5。
[0136]
在总体层面上，各rdd完成各自种群的迭代计算之后，需要进行各种群间的信息交互，即找出全部种群上一次迭代计算时产生结果中的最优解；如果该解比当前全部种群的最优解还好，则更新当前最优解，并且将最优解继续传递到下一次的各个种群的迭代计算中。
[0137]
在本发明一具体实施例中，采用14节点配电网测试系统作为算例系统进行分布式电源的选址和定容分析。
[0138]
如图3所示，分布式电源待安装节点位置为3，4，10，14，该系统的电压等级为23kv，p
total
＝28.7mw，q
total
＝7.75mvar。按照p
dg
≤0.25p
total
，取p
dg
＝3mw，cosφ＝0.9，每台分布式电源的额定功率为200kw，电压偏差规定在
±
5％以内。第i个dg的安装成本c
dg1i
＝1344元/kw；第i个dg的运行维护费用成本c
dg2i
＝0.052元/kw；第i个dg的发电燃料费用成本c
dg3i
＝0.3元/kw。
[0139]
表1为采用dide算法进行分布式电源选址和定容得到的最优方案。从表1可看出根据dide算法找出分别在:3，4，10，14节点安装电源，且最优输出功率分别为799.3，167.1，
400，194.9kw。根据实际设备制造情况，3，4，10，14节点应该分别安装4，1，2，1台分布式电源。每台分布式电源的额定功率为200kw。在无分布式电源时网络的有功网损为0.5172mw，网络的最低电压为0.9713pu，平均电压为0.9842pu；优化后的有功网损为0.4131mw，网络的最低电压为0.9740pu，平均电压为0.9854pu。对比无分布式电源时，网络的有功网损降低了20.1％，有效节省了电网的运行费用，这对实现配电网的经济稳定运行有着重要的影响。
[0140]
表1采用dide算法优化14节点系统dg安装位置和容量
[0141]
安装位置最优输出功率/kw安装台数/台功率因数100-200-3799.340.94167.110.9500-600-700-800-900-10400.020.91100-1200-1300-14194.910.9合计1561.38-[0142]
通过表1可知采用本发明的分布式电源规划方法充分利用分布式集群的计算资源，提高算法的搜索效果；以分布式电源建设和运行总费用最小为优化子目标的规划模型，实现配电网测试系统进行分布式电源最优规划。
[0143]
采用最优规划方案，不但能够有效地降低网络的有功网损，减少分布式电源的建设和运行费用，而且还可以提高系统的电压水平。
[0144]
上述实施例仅供说明本发明之用，本技术领域的普通技术人员，在不脱离本发明的精神和范围的情况下，还可以作出各种变换或变化，因此，所有等同的技术方案也应该属于本发明的范畴。