一种基于刚度等效和模型降阶的减振优化快速计算方法

本发明属于航空航天中主承力薄壁构件减振优化设计领域，提出一种基于刚度等效和模型降阶的减振优化快速计算方法。

背景技术：

薄壳结构广泛用于航空航天承力部件，如运载火箭燃料贮箱、飞机机身、航空发动机加力筒体等。典型的薄壳结构包括柱壳、锥壳、球壳、组合壳等。典型的服役工况包括轴压、外压、扭转、轴内压、轴外压、轴扭转等。同时薄壁结构除了承受静态载荷以外，还承受不同类型的动力载荷，在其使用期间，不可避免地受到外界环境的振动干扰，动力损伤是其主要的破坏形式之一。在部分航天部件的运行过程中，还会要求其固有频率远离发动机振动频率，并保证一定的抗击振动能力。

对于大型复杂结构，其动载荷下的力学分析计算量比静力分析大几个数量级，求解过程极其耗费时间，构造合适的降阶模型能够在大幅度降低计算时间的同时保证计算动力分析的精度，并解决大型复杂结构的多约束多工况优化迭代中大量动力学计算非常耗时的问题。同时对于复杂薄壁结构的分析和优化，其快速承载力预测的需求也变得日益迫切。

为了改善结构或者系统的动态特性，达到控制振动的目的，确保其动力环境下的工作安全可靠，开展动力优化设计方面的研究和应用变得日益迫切，发明一种在研发阶段就考虑动力性能并进行减振优化，并综合结构的承载力，多变量协同化设计，实现轻量化目标的快速优化计算方法尤为重要。

技术实现要素：

本发明主要解决复杂薄壁加筋结构协同承载力和动力需求实现轻量化设计耗时巨大的问题，提出一种基于刚度等效和模型降阶的减振优化快速计算方法。

针对优化区间范围内的复杂薄壁加筋结构，首先划分周期性单胞结构，并建立原薄壁加筋结构同尺寸不含筋条的光筒薄壁结构。然后，对单胞结构求解得到等效刚度系数，针对加筋薄壁结构整体屈曲载荷预测得到承载力，对单胞提取质量并经过乘积计算得到模型整体质量，并采用面积等效方法得到等效密度。进而，将等效密度和等效刚度赋予到光筒模型，使用模型降阶方法结合全局减缩基技术，建立降阶数值分析模型，对降阶后的模型进行动力学分析，计算得到特定工作频段能量值。最后，以加筋薄壁结构的壳体厚度和筋条参数为设计变量，结构承载力和工作频段能量值作为约束，质量最轻为目标进行优化设计。

为了达到上述目的，本发明的技术方案为：

一种基于刚度等效和模型降阶的减振优化快速计算方法，包括以下步骤：

第一步，针对复杂加筋薄壁结构划分有限元周期性加筋单胞结构，并建立原薄壁加筋结构同尺寸不含筋条的光筒薄壁结构，具体如下：

首先，建立复杂加筋薄壁结构，从加筋薄壁结构中划分出代表性周期加筋单胞结构，得到单胞有限元模型，其中单胞结构主要包括蒙皮和筋条两个部分。其次，根据原加筋薄壁结构，建立同样尺寸去除筋条的光筒薄壁结构。最后，对单胞结构和光筒薄壁结构有限元单元网格划分，并对单胞结构赋予材料属性。

第二步，基于有限元单胞计算得到等效刚度系数、等效密度、模型整体结构质量以及结构承载力，具体如下：

根据单胞有限元模型，基于渐进均匀化理论或者等效刚度法求解加筋单胞的等效刚度系数，将等效刚度系数带入瑞利-里兹公式，求解整体结构线性屈曲载荷值，即为结构承载力。对单胞有限元模型查询质量，用单胞质量除以单胞蒙皮面积得到等效密度，用单胞质量乘以单胞数量得到模型整体结构质量。

第三步，将第二步求得的等效刚度系数和等效密度参数赋予划分网格后的光筒薄壁结构，建立等效模型，基于模型降阶方法结合全局减缩基技术建立降阶分析模型，进行动力学谐响应分析，得到特定工作频段能量值，具体如下：

首先，将第二步求得的等效刚度和等效密度赋给第一步建立的光筒薄壁结构，获得复杂加筋薄壁结构的等效模型。然后，通过减缩基构造方法构造结构初始减缩基矩阵，再使用模型降阶方法结合全局减缩基技术建立全局减缩基矩阵，通过降低有限元数值计算模型的维度建立降阶分析模型，对有限元数值模型进行自由度减缩，使降阶模型在满足分析精度的同时减少计算时间。最后，对降阶后的模型进行动力学谐响应分析，根据谐响应分析得到的的动刚度和位移响应输出计算频点的能量，对特定工作频段内的所有能量值进行累加得到工作频段能量值。

进一步的，所述减缩基矩阵构造方法包括里兹向量法、模态叠加法。

进一步的，所述的模型降阶方法包括：特征正价本征正交分解(properorthogonaldecomposition，pod)方法、动力学模态分解(dynamicmodedecomposition，dmd)方法。

第四步，建立承载力与动响应协同优化列式并对优化问题进行求解。以加筋薄壁结构的壳体厚度和筋条参数为设计变量，第二步和第三步中得到的结构承载力和工作频段能量值作为约束，质量最小化为目标进行轻量化设计。

建立的轻量化优化列式如下：

find：x

minimize：mass

subjectto：xi^lb≤xi≤xi^ub,i＝1,...i

pcr(x)＞pini

te(x)＜teini

式中，x为设计变量，包括加筋薄壁结构的壳体厚度和筋条参数；xi^lb和xi^ub分别是变量x的下限值和上限值。mass为待求结构整体质量，pcr(x)和te(x)分别是待求结构整体承载力和工作频段内的总能量，pini和teini分别是原始构型的整体承载力和工作频段能量值。

四步中在优化计算方法上，首先，采用聚类方法对优化设计空间减缩，以便于寻优。其次，根据缩小范围之后的参数变量区间进行局部寻优处理。最后，采用局部优化方法求解最优解，经过优化得到满足结构承载力许可，得到实现减振功能性需求和轻量化设计的最优构型。

进一步的，所述的聚类方法包括:k均值聚类方法、模糊c均值聚类方法、som神经网络聚类方法。

本发明的有益效果为：本发明针对复杂薄壁加筋结构协同承载力和动力需求实现轻量化设计耗时巨大的问题，通过对复杂加筋薄壁结构划分周期性加筋单胞结构，求解等效刚度系数和等效密度，基于整体屈曲载荷预测方法和快速质量计算方法快速获得结构承载力和质量信息，基于等效模型与模型降阶方法结合全局模型降阶技术实现快速动力学谐响应分析，并在优化求解过程中使用聚类方法对设计变量空间减缩，加速了优化进程，快速求解，实现综合考虑结构承载力、动力学响应协同优化设计的目的。本发明提出的方法能实现复杂薄壁加筋结构减振轻量化快速计算，实现结构承载力和动力学响应协同设计，在满足结构功能需求的同时，减轻结构质量，缩短设计时间周期，降低材料成本，提高经济效益。

附图说明

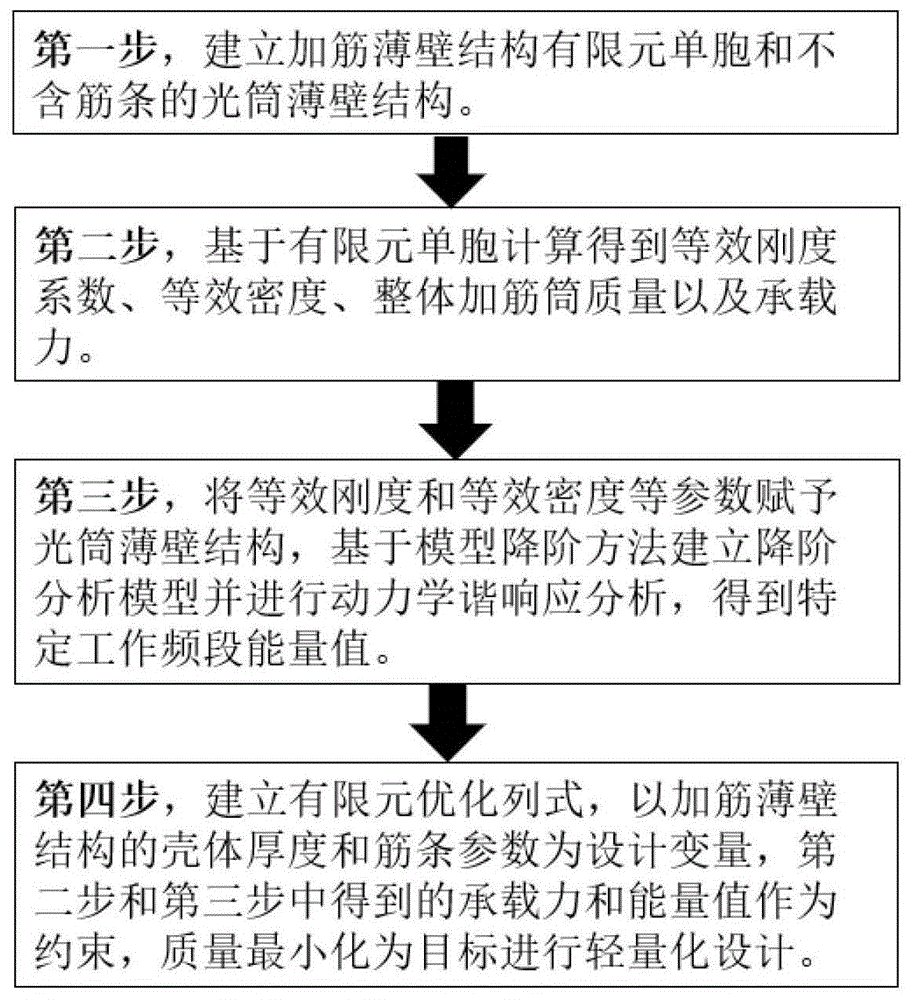
图1为本发明的实现流程图；

图2为本发明加筋薄壁模型实例提供的初始设计构型：图2(a)为正置正交加筋圆柱壳模型，图2(b)为不含筋条的光筒薄壁模型，图2(c)为周期性加筋单胞结构模型。

具体实施方式

为使本发明解决的方法问题、采用的方法方案和达到的方法效果更加清楚，下面结合附图和实施例对本发明作进一步的详细说明。可以理解的是，此处所描述的具体实施例仅仅用于解释本发明，而非对本发明的限定。另外还需要说明的是，为了便于描述，附图中仅示出了与本发明相关的部分而非全部内容。

如图1所示，本发明实施例提供的一种基于刚度等效和降阶模型的减振优化快速计算方法流程图，包括：

第一步，针对复杂加筋薄壁结构划分有限元周期性加筋单胞结构，并建立原薄壁加筋结构同尺寸不含筋条的光筒薄壁结构。

首先，建立正置正交加筋圆柱壳薄壁结构模型，从加筋薄壁结构中划分出代表性单胞结构，并建立单胞有限元模型，单胞结构主要包括蒙皮和筋条两个部分，加筋圆柱壳薄壁结构壳体模型直径d＝9000mm，壳体高度为h＝600根据0mm，蒙皮厚度ts＝6.0mm，筋条高度为hr＝15.0mm，筋条厚度为tr＝9.0mm，纵向筋条数目为num_a＝180，环向筋条数目为num_c＝40，用柱壳圆环周长πd除以纵向筋条数目得到单胞横边边长na，用高度h除以横向筋条数目得到单胞纵向边长nc，建立单胞有限元模型。在有限元软件中建立同样直径d＝9000mm，高度为h＝6000mm的光筒薄壁结构模型，进行有限元网格划分，单元为尺寸80mm的s4r单元，模型材料采用各向同性的铝合金材料。图2(a)为正置正交加筋圆柱壳模型，图2(b)为不含筋条的光筒薄壁模型，图2(c)为周期性加筋单胞结构模型。

第二步，基于渐进均匀化快速数值实现方法(novelimplementationofasymptotichomogenization)，计算单胞结构的等效刚度系数，即拉伸刚度系数aij、耦合刚度系数bij、弯曲刚度系数dij，将上述等效刚度系数带入瑞利-里兹公式，计算得到整体屈曲载荷值16558kn。在软件查询单胞质量作为输出，用单胞质量除以单胞蒙皮的面积(横向边长与纵向边长乘积)得到将筋条抹平到蒙皮上的等效密度，用单胞质量乘以单胞数量即为模型整体质量，整体质量为3554kg。

第三步，将划分好的光筒模型网格信息导入到matlab软件中，将第二步求解的等效刚度系数和等效密度信息赋予第一步的光筒薄壁结构模型，获得复杂加筋薄壁结构的等效模型，固定底端所有节点，对上端面所有结点x、y、z三个方向施加100n的载荷激励进行谐响应分析，基于光筒等效模型，组装刚度阵kt、质量阵m和阻尼阵c，阻尼选取瑞利阻尼，阻尼阵为c＝0.01*m+0.0001*kt。基于拉丁超立方采样(latinhypercubesampling,lhs)方法策略在设计空间得到50个样本构型，根据载荷相关的里兹向量法(load-dependentritzvector，ldr)构造里兹向量形成初始减缩基矩阵，再使用本征正交分解(properorthogonaldecomposition，pod)降阶方法结合全局减缩基技术构建全局减缩基矩阵，任一结构的频响分析均利用全局减缩基矩阵实现矩阵降维，这大幅提高了结构减振优化效率，全局减缩基矩阵列数296列，使得刚度阵kt，质量阵m，阻尼阵c从1483920*1483920的方阵转换为296*296的方阵，而外载荷向量nf从1483920*1的方阵转换296*1的向量。计算区间能量选取的工作频段区间为[62.5hz,72.5hz]，每隔0.25hz取一个采样点，一共41采样点，计算每个采样点的频率对应的能量值l(x,ωc)，对每个采样点能量值累加，计算得到工作频段的总能量值为3316.7db。

第四步，基于降阶模型的减振优化设计。

基于刚度等效和模型降阶技术可以很快速计算求解加筋模型的承载力、质量以及频段能量信息，为减振优化快速计算做好了准备工作，综合考虑结构承载力和动响应，进行轻量化设计。承载力与动响应协同优化列式如下：

find：x

minimize：mass

subjectto：xi^lb≤xi≤xi^ub,i＝1,...i

pcr(x)＞pini

te(x)＜teini

式中，x是设计变量，xi^lb和xi^ub分别是变量x的上限值和下限值。mass为模型整体质量，pcr(x)和te(x)分别是待求结构x的整体承载力和工作频段内的总能量，pini和teini分别是减振原始构型的整体承载力和工作频段内的总能量。

其中nf表示外激励频点的数目，是通过降阶模型得到的在频点ωc处的能量。

在优化计算方法上，先采用模糊c均值(fuzzyc-means)算法对优化设计空间减缩，以便于快速寻优计算。再根据缩小范围之后的参数变量区间进行局部寻优处理，采用的方法为序列二次规划(sqp)方法。

数值实验中，正置正交加筋圆柱壳薄壁结构模型，初始模型的各项参数xini＝[6.09.015.040180]，参数向量中的数值，分别对应为蒙皮厚度ts、筋条厚度tr、筋条的高度hr、轴向筋条数目numa和环向筋条数目numc。结构初始质量为3554kg,，结构承载力为16558kn，工作频段区间[62.5hz,72.5hz]内总能量为3316.8db。

优化变量区间下限x^lb＝[4.04.05.025140]，优化变量区间上限x^ub＝[8.012.025.050200]，其中轴向和环向筋条数目取整数。

优化后最优构型对应的参数x＝[5.644.4023.1331148]。

最优构型的质量为3058.8kg，相较原始结构重量3554kg，减重了495kg，减重率为14.0％。承载力pcr(x)＝16559kn>16558kn，工作频段能量te(x)＝3316.2db<3316.8db，均满足约束条件。实现了结构承载力和动力学响应协同设计，在满足结构功能需求的同时，减轻了结构质量，缩短了设计时间周期，降低了材料成本，提高了经济效益。

最后应说明的是：以上各实施例仅用以说明本发明的方法方案，而非对其限制；尽管参照前述各实施例对本发明进行了详细的说明，本领域的普通方法人员应当理解：其对前述各实施例所记载的方法方案进行修改，或者对其中部分或者全部方法特征进行等同替换，并不使相应方法方案的本质脱离本发明各实施例方法方案的范围。