一种考虑准备时间和工件分批的柔性作业车间调度方法与流程

本发明涉及应用于柔性作业车间调度技术领域，特别涉及一种考虑准备时间和工件分批的柔性作业车间调度方法。

背景技术：

车间调度是制造系统的基础，在满足约束条件的情况下，通过优化生产性能指标，充分利用生产资源合理地安排不同种类工件的作业加工次序，以缩短生产时间，降低企业的生产成本，提高企业的竞争力。柔性作业车间调度问题(flexiblejobshopschedulingproblem，fjsp)是作业车间调度问题(jobshopschedulingproblem，jsp)的扩展。在fjsp问题中，机器的柔性提高了作业车间的执行效率，同时，扩大了可行解的范围，增加了问题的难度。目前，关于作业车间调度问题的研究主要体现在采用遗传算法解决工序排序问题上。但是结合作业车间实际生产过程，仍然存在以下问题：

1、车间生产过程中，生产准备过程需要一定的生产准备时间，进行刀具的准备、更换及机床调整等工作；2、工件批量加工时，多采用等量分批方式进行批量分割，工件的子批数量和子批批量缺乏柔性；3、工件的批量划分和工序调度优化之间是分离的。

技术实现要素：

为了解决以上技术问题，本发明的目的在于提供一种考虑准备时间和工件分批的柔性作业车间调度方法，该方法考虑了工件在加工过程中需要准备时间以及工件批量加工时需要分批的情况，将两者结合到一起，合理地安排各工件的加工路线，以实现最大加工时间的最小化，提高生产效率，用于支持柔性作业车间调度决策。

为了实现上述目的，本发明采用的技术方案是：

一种考虑准备时间和工件分批的柔性作业车间调度方法，包括以下步骤：

步骤1：根据柔性作业车间调度特点，建立考虑准备时间和工件分批的柔性作业车间调度模型；

步骤2：采用fr分批方法对工件进行批量划分；

步骤3：采用改进的遗传算法求解模型，得到最大完工时间的最小值，所述遗传算法求解模型包括编码、解码、选择、交叉和变异。

所述步骤1中考虑准备时间和工件分批的柔性作业车间调度模型中的符号定义；根据柔性作业车间工件批量加工的特点，建立约束条件，建立目标函数；

所述步骤2中fr分批方法是指工件批量加工时，对工件进行批量划分的柔性分批方法。

所述步骤3中编码是指用于解决工件分批和各工件子批工序调度排序问题的双层编码方法。

所述步骤3中解码是指先对上层编码中的工件分批编码进行解码，再对子批工序调度编码和机器选择编码进行解码。

所述步骤3中选择采用锦标赛选择方式对染色体的基因进行选择，保留种群中的最优个体。

所述步骤3中交叉是指在双层编码中，对上层工序分批编码部分进行单点交叉操作。

所述步骤3中变异是通过随机改变染色体上的某些基因以产生新的个体，增加种群的多样性。

本发明的有益效果：

针对柔性作业车间调度问题，通过步骤1建立考虑准备时间和工件分批的柔性作业车间调度模型，将柔性作业车间调度问题用数学模型表示，使柔性作业车间调度问题更加清晰和具体化；

fr分批方法有效地解决了等量分方法对工件进行批量分割时工件的子批数量和子批批量缺乏柔性的问题，使得工件批量加工时具有很大的柔性，更加符合生产实际情况，提高了车间生产效率；

采用改进的遗传算法对模型进行求解，提高了模型求解的收敛速度和运行效率，可有效对工件的批量划分和总排产时间进行优化；

考虑了工件的加工准备时间，更加符合实际车间生产要求。

附图说明

图1为本发明染色体编码示意图。

图2为本发明调度甘特图。

具体实施方式

下面结合附图对本发明作进一步详细说明。

如图1、图2所示：

步骤1：建立考虑准备时间和工件分批的柔性作业车间调度模型；

step1，所述柔性作业车间调度问题可描述为：有n种工件在m台机器上加工，每种工件可批量划分为若干子批，各子批次批量数随机分配；每种工件各子批次的每道工序可按照一定的工艺次序在若干台机器上进行加工，具有柔性的加工路径，各子批次工件不同工序之间需要一定的加工准备时间。

step2，考虑准备时间和工件分批的柔性作业车间调度模型中的符号定义：

n：待加工工件的种类；

m：机器的数量，机器集m＝{m1，m2，m3，...mm}；

j：第i种工件的批次号(i＝1，2，...，n)；

k：工件i的工序号；

bi：工件i的加工数量；

pi：工件i的子批数量；

sij：工件i第j批次的批量数；

oik：工件i的第k道工序(k＝1，2，...，toi)，toi为工件i的总工序数；

tijkm：工件i第j批次第k道工序在机器m上的加工开始时间；

eijkm：工件i第j批次第k道工序在机器m上的加工结束时间；

stikm：工件i第k道工序在机器m上的加工准备时间；

ptikm：工件i第k道工序在机器m上的实际加工时间；

eijtm：工件i第j批次最后一道工序在机器m上的加工结束时间；

xijkm：若工件i第j批次第k道工序在机器m上加工则为1，否则为0；

ci：工件i的完工时间；

cmax：所有工件的最大完工时间。

step3，根据柔性作业车间工件批量加工的特点，建立约束条件：

约束1：各工件子批的每道工序只能在一台机器上加工

约束2：同一种工件分批之后，工件的总数不变

约束3：工件i第j批次第k道工序在机器m上的加工结束时间eijkm等于加工开始时间、加工准备时间和实际加工时间之和

eijkm＝tijkm+stikm+ptikm×sij(3)

约束4：各工件子批按照特定的工艺路线进行加工

tij(k+1)m≥eijkm(4)

约束5：工件i的最大完工时间等于各子批最后一道工序完工时间的最大值

ci＝max(eijtm)，j＝1，2，...，pi(5)

step4，建立模型的目标函数，表达式如下：

mincmax＝max{ci|i＝1，2，...，n}(6)

本方法以工件的最大完工时间为优化目标建立目标函数，求得最大完工时间的最小值。

通过步骤1，将考虑准备时间和工件分批的柔性作业车间调度问题转化为具体的数学模型，建立相应的约束关系和目标函数。

步骤2：针对柔性作业车间调度模型，建立求解算法。

fr分批方法

fr(flexiblerandom)分批方法，可以解决机器负荷不均匀等问题，提高生产效率。具体分批步骤如下：

step1：由决策者给定子批数量范围a至b(a与b均为整数且0＜a＜b，)，算法在此范围内产生随机整数m；

step2：算法在1至n范围内随机产生第1个整数c1(1≤c1≤n)，置i←c1，j＝1；

step3：判断c1是否满足i+m-j≤n，若满足，则继续下一步，反之，则返回到step2；

step4：算法在n-i至n范围内随机产生第2个整数c2(n-i≤c2≤n)，则i←i+c2，j＝2；

step5：判断c2是否满足i+m-j≤n，若满足，则继续下一步，反之，则返回到step4；

step(2m-2)：算法在n-i至n范围内随机产生第m-1个整数cm-1(n-i≤cm-1≤n)，则i←i+cm-1，j＝m-1；

step(2m-1)：判断cm-1是否满足i+m-j≤n，若满足，继续下一步，反之，则返回到step(2m-2)；

step2m：计算cm＝n-i。

采用fr分批方法将n个工件分成m个子批，各子批批量为(c1，c2，…，cm)。假设n＝12，a＝1，b＝4，产生的随机数m＝3，按照以上分批算法，若产生的一组数(c1，c2，c3)＝(4，2，5)，则该工件被分为3批，各子批对应的批量为(4，2，5)。在算法运算过程中，fr分批方法可以使工件子批数量和子批批量得到柔性调节，在子批数量不增加，算法求解效率不降低的前提下，能够有效缩短生产周期，平衡机器负荷，提高生产效率。

步骤3具体为：

step1，编码

本方法采用双层编码的方式解决工件分批和各工件子批工序调度排序的问题，染色体由两层组成，每层染色体各由两部分组成。第一层前一部分表示工件分批编码，后一部分表示各工件子批的工序排序编码。在第二层编码中与工件分批编码对应的部分用无意义的“0”表示，机器选择部分要与第一层的工件子批工序排序部分一一对应。有3种工件，分批方式为(3，2，2)，表1为工序编码中数字对应的各工件的子批。

表1工序编码中数字1-7对应的各工件子批

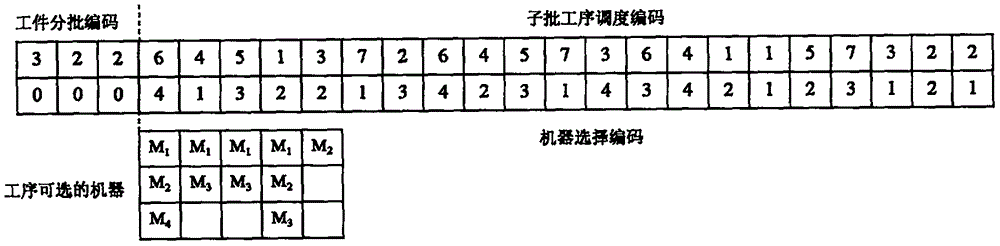
采用双层编码方式进行编码时，其中一条染色体如图1所示。

在图1所示的染色体编码中，3种工件的分批方案为(3，2，2)。染色体上层为工件分批编码和子批工序调度编码，在工件子批工序调度编码中，第一次出现的6表示工件3的第1个子批的第1道工序，第二次出现的6表示工件3的第1个子批的第2道工序。oijk示工件i第j批次的第k道工序，则上层编码对应的工序顺序是

o311-o211-o221-o111-o131-o321-o121-o312-o212-o222-o322-o132-o312-o213-o112-o113-o223-o323-o133-o122-o123。在第二层机器选择编码中，工序o311有3台机器可以选择，编码中的4表示在机器m4上加工。

step2，解码

染色体的解码过程是将染色体转化为工件工序的调度解，主要是解决工件各子批工序排序问题和机器选择问题。在对染色体进行解码时，先对工件分批编码部分进行解码。对机器选择部分进行解码时，从左到右依次读取染色体的机器编码，转换为机器矩阵jm、工件加工时间矩阵t1和机器准备时间矩阵t2。在对工序排序进行解码时，从左到右读取染色体的子批工序调度编码部分。解码过程中要对工件的加工结束时间eijkm与机器的空闲时间段进行比较，之后在可加工该道工序的所有机器中选择完工时间最早的机器。

step3，选择

遗传算法的每一次迭代都需要用选择算子选择出需要进行交叉或变异的个体，选择适当的个体进入下一代。选择算子有不同的性质和适应范围，由优化调度目标确定选择策略。本算法把目标函数的倒数作为适应度函数，即：

采用锦标赛选择方式对染色体的基因进行选择，保留种群中的最优个体。

step4，交叉

遗传算法的交叉操作是将父代染色体的基因交换组合之后产生新个体，交叉操作决定了遗传算法的性能。在双层编码中，上层子批工序调度编码的改变会引起下层机器选择编码的改变。因此，在进行交叉操作时只需对上层子批工序调度编码进行交叉操作。对工件子批工序调度编码进行交叉操作时，首先根据交叉概率选择两条染色体，交叉时采用单点交叉的方法，即交换父代两条染色体交叉点之后的工件分批编码。交叉后必然会产生非法染色体，因此需要对染色体进行修复。若进行交叉后子批数量增加，需在染色体工序调度编码任意位置随机插入缺少的基因位；若子批数量减少，需删除染色体工序调度编码里多余的基因位，同时下层机器编码也应随之调整，使之与子批工序调度编码一一对应。

交叉操作流程如下：

step1：随机选取两条父代染色体q1、q2，分别计算工件总子批数量记为a(a1、a2)，并在染色体的工件分批编码处随机生成一个pos位置，并交换pos位置后的工件分批编码形成j1、j2两条染色体；

step2：分别计算j1、j2两条染色体的工件总子批数量记为b(b1、b2)，设i＝{1，2}；

step3：1.若ai＞bi，则ji的总子批数量减少，需要删除ji里多余的基因位，转step4.1；

2.若ai＜bi，则ji的总子批数量增加，需要插入ji里缺少的基因位，转step4.2；

step4：1.保留染色体ji工序调度编码里值小于等于bi的基因位，删除大于bi的基因位得到子代hi；

2.将染色体ji工序调度编码里值最大的基因位与bi相比，得到需要插入的基因位，并在ji的工序调度编码里随机插入缺少基因位得到子代hi；

step5：下层机器编码进行调整。

变异

变异操作是通过随机改变染色体上的某些基因以产生新的个体，增加种群的多样性。同交叉操作一样，只需对子批工序调度编码部分进行变异操作。

(1)对上层编码中的子批工序调度编码进行变异操作时，随机选择子批工序调度编码中的一个基因位，并为该基因位赋予一个子批数量范围内的新值。若产生非法染色体，则采用交叉操作时的修复方法对染色体进行修复；

(2)对子批工序调度编码进行变异操作时，采用两点换位法，即随机交换两个子批工序调度编码和其对应的机器选择编码。

以具体的柔性作业车间调度实例来说明本发明的实用性和有效性。表2为一个4x6型柔性作业车间调度问题实例，该调度问题中有4种工件，在6台机器上加工，每种工件有8个，每个工件有3道工序，每道工序均可被多台机器加工。

采用表2中的数据，用本方法进行求解时，各工件分批方案的最大完工时间如表3所示。

表3各工件分批方案及最大完工时间

结合实际车间生产要求，工件在不同机器上加工时，工件的安装、定位及刀具的更换等需要加工准备时间。在表3数据的基础上，添加工件的加工准备时间。工件分批加工时工序的准备时间等于工序单个工件的加工时间。在考虑准备时间和工件分批的情况下，用本方法求解时，求得最大完工时间的最优值为99，其最优分批调度方案为(4，1，4，4)，第2种工件不分批，其余工件均分为4批，各批次的批量数为：(2，3，2，1)、(2，2，2，2)、(3，1，2，2)。对应调度方案的甘特图如图2所示。

在图2中，黑色部分表示工件的加工准备时间，f5为第2种工件，首次出现在机器m5上，表示第2种工件的第一道工序在机器m5上加工。f7为工件3的第2个子批，最后一道工序在机器m5上完成，完工时间为99。