一种海洋油气水平管线支吊架安装间距的优化方法与流程

1.本发明涉及管线安装方法，尤其涉及一种海洋油气水平管线支吊架安装间距的优化方法。


背景技术：

2.管线安装需要确保管系安全可靠，在进行管线安装设计时，除做到管线布置满足要求并安排合理外，还应合理设置支吊架。管线支吊架间距计算是管线设计中的重要环节，只有在满足标准、保证安全可靠的前提下，合理选择支吊架间距，才能达到高质量、低造价的目的。
3.目前国内在进行管线支吊架设计时，主要是以几种国家标准推荐的公式及数据为基础，但由于某些标准表达地较为含糊，各标准中的计算方法也略有不同，各有优缺点，即使是针对同一条管线，按不同方法计算后得出的结论也存在一定的差异，在设计时需要查阅各种标准进行比较，没有完善的、合理的、统一的计算方法。除此之外，由于标准中通常只考虑支吊架及管线的力学特性，没有把实际工程的经济因素考虑在内，对于实际设计，在满足标准要求后，工程师通常根据经验最后确定支吊架的间距。传统设计过程费时费力，且设计结果也不一定准确，效率、质量较低。


技术实现要素：

4.本发明的目的在于克服已有技术的缺点，提供一种既能满足安装支撑强度要求，又高效可靠且成本低的海洋油气水平管线支吊架安装间距的优化方法。
5.为了达到上述目的，本发明采用的技术方案是：
6.本发明的一种海洋油气水平管线支吊架安装间距的优化方法，包括以下步骤：
7.步骤一、设定吊装水平直管线的支吊架的结构，所述的支吊架的结构为龙门式支吊架；
8.步骤二、根据已知实际工况预先确定水平直管线的基本参数作为优化支吊架间距的已知条件，所述的基本参数包括工作温度、管线的材质、管线的质量、管线的设计压力、管线外径、管线内径和管线长度；
9.步骤三、对相邻的两个支吊架之间的间距进行优化，优化过程如下：
10.第一步，根据工作状态下对水平直管线在持续荷载下产生的一次应力σ
l
的设计要求，由公式(1)计算得出沿水平直管线的长度方向设置的相邻的两个支吊架间距l的初始范围；
[0011][0012]
式中：p为管内工质设计压力，mpa；d1为管线外径，mm；d2为管线内径，mm；q为管线单位长度重力载荷，n/m；w为管线的截面抗弯矩，mm3，按计算；[σ]
t
为管线所用材料在设计温度t℃时的许用应力；
[0013]
第二步，利用matlab软件确定两个相邻支吊架之间的最佳的间距l；
[0014]
(a)在matlab中建立两个相邻支吊架的间距l变量,将第一步确定的l
max
赋值给变量l；
[0015]
(b)在matlab中按如下步骤进行计算：
[0016]
步骤101，将变量l代入式(2)中进行计算，得到m
c
；
[0017][0018]
式中，m
c
为是热胀引起的合成力矩范围，n
·
m；fx为水平管线在x方向上所受的力，fx＝eε
x
a
x
，e为20℃时的弹性模数，ε
x
为水平管线在x方向上的应变，a
x
为水平管线在x方向受力面积，n；fy、fz分别为水平管线在与x方向垂直的y方向与z方向上所受的力，n，计算方法同fx；
[0019]
步骤102，将m
c
代入式(3)中进行计算，得到与l值对应的二次应力值σ
e
；
[0020][0021]
式中，σ
e
为管线热胀应力范围即二次应力，mpa；i为应力增加系数，对于所述水平直管线，0.75i等于1；
[0022]
步骤103，将l值代入，计算不等式σ
e
≤f[1.2[σ]
20
+0.2[σ]
t
+([σ]
t
‑
σ
l
)]右侧的值，然后与上一步得到的σ
e
比较，判断是否满足不等式条件，若满足条件，则保留该l值的数据，否则舍弃该l值；
[0023]
式中，[σ]
20
为管线所用材料在20℃时的许用应力，mpa；[σ]
t
为管线所用材料在设计温度t℃时的许用应力，f为应力范围减小系数；
[0024]
一次应力σ
l
按下式(4)计算：
[0025][0026]
步骤104，将l值代入中进行计算，得到该l值所对应的成本值c；
[0027]
式中,c为成本值；c0为成本系数；l为管线的长度，l为相邻两个支吊架之间的间距，即表示一条管线所设置的支吊架总的个数；
[0028]
(c)逐渐减小第二步(a)中相邻的两个支吊架间距l，重复第二步(b)，进行迭代计算，直至l减小至负值，结束迭代计算；
[0029]
(d)将每个已保留的l值所对应的成本值c及σ
e
代入中计算，得到与每个已保留的l值所对应的价值v；
[0030]
式中，v为综合考虑二次应力σ
e
与成本c的加权价值；a为二次应力的权重系数；b为成本的权重系数，a、b值根据所述两个因素的重要程度进行赋值，a+b＝1；
[0031]
(e)在上述的所有l值中选取使得v值最小的l值作为相邻两个支吊架的最佳间距；若所有l值下的二次应力均不满足上述不等式σ
e
≤f[1.2[σ]
20
+0.2[σ]
t
+([σ]
t
‑
σ
l
)]的要求，则根据设计经验更换步骤二中的基本参数，然后返回到步骤三重新计算，直至取得支吊架最佳间距；
[0032]
步骤四、根据步骤三确定的支吊架间距尺寸及步骤二确定的基本尺寸利用
solidworks建立管线及支吊架的三维模型，并将模型导入ansys软件中进行有限元仿真分析，输出仿真得到的支吊架能承受的最大应力及应变值，最后将输出的所述最大应力及应变值与管线在实际工作过程中能承受的极限应力及应变值比较，如果满足实际工作需求，则该支吊架模型合格，直接导出模型，根据所述模型进行实际安装即可；若不满足要求，则根据设计经验更换步骤二的基本参数，然后重复步骤三和步骤四，直到满足要求为止。
[0033]
与现有技术相比，本发明具有以下有益效果：
[0034]
本发明方法可以有效地解决传统支吊架间距设计效率低且设计结果不准确的问题。利用计算机软件计算和分析功能，设计人员只需输入关键参数就能得出结果，保证了设计的快速性和准确性，同时能满足支吊架在安装使用时的强度要求，并有效降低工程成本。
附图说明
[0035]
图1是安装水平管线支吊架的结构示意图；
[0036]
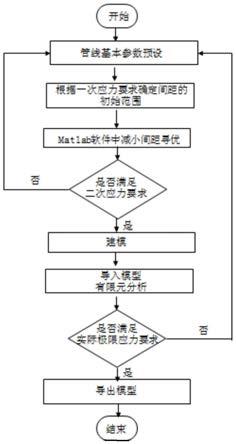
图2是本发明的一种海洋油气水平管线支吊架安装间距的优化方法的流程图。
具体实施方式
[0037]
下面结合具体实施例对本发明进行详细描述。
[0038]
本发明的一种海洋油气水平管线支吊架安装间距的优化方法，包括以下步骤：
[0039]
步骤一、设定吊装水平直管线2的支吊架1的结构，所述的支吊架的结构为龙门式支吊架；
[0040]
步骤二、根据已知实际工况预先确定水平直管线的基本参数作为优化支吊架间距l的已知条件，所述的基本参数包括工作温度参数t、管线的材质、管线的质量、管线的设计压力p、管线外径d1、管线内径d2和管线长度l，以上基本参数由前期工程设计得到，均为已知；
[0041]
步骤三、对相邻的两个支吊架之间的间距进行优化，优化过程如下：
[0042]
第一步，根据工作状态下对水平直管线在持续荷载(如：内压、自重和其他持续外载)下产生的一次应力σ
l
(所述的一次应力为轴向应力之和)的设计要求，由公式(1)计算得出沿水平直管线的长度方向设置的相邻的两个支吊架间距l的初始范围；
[0043][0044]
式中，p为管内工质设计压力，mpa；d1为管线外径，mm；d2为管线内径，mm；q为管线单位长度重力载荷，n/m，由管线总质量除以总长度得到，上述总质量与总长度在管线的前期设计阶段已知；w为管线的截面抗弯矩，mm3，按计算；[σ]
t
为管线所用材料在设计温度t℃时的许用应力，根据设计温度t查阅国家标准gb50316
‑
2000附录a可得。
[0045]
上式的推导过程如下：
[0046]
一次应力σ
l
满足以下要求：
[0047][0048]
式中,p为管内工质设计压力，mpa；d1为管线外径，mm；d2为管线内径；m
a
为由于管线
自重和其他持续外载(如外界风雪载荷、船舶振动载荷等)作用在管线横截面上的合成力矩，n
·
m，当水平直管线的相邻支吊架间既有管线单位长度重力载荷q又有管内设计压力p作用时，m
a
按照m
a
＝ql2/8+pl/4进行计算；i为应力增加系数(按行业标准dl/t5366
‑
2006的附录c中取值)，0.75i不小于1，对于所述水平直管线0.75i等于1；[σ]
t
为管线所用材料在设计温度t℃时的许用应力，根据设计温度t查阅国家标准gb 50316
‑
2000附录a可得。
[0049]
按上述要求，式(2)可以转化为：
[0050][0051]
在实际工程设计中，两个相邻支吊架间只有q没有p的情况较为多见，因此这项可以忽略，此时式(2)可以进一步简化为所述公式(1)：
[0052][0053]
第二步，利用matlab软件确定两个相邻支吊架之间的最佳的间距l；
[0054]
(a)在matlab中建立两个相邻支吊架的间距l变量，将第一步确定的l
max
赋值给变量l；
[0055]
(b)在matlab中按如下步骤进行计算：
[0056]
步骤101，将变量l代入式(4)中进行计算，得到m
c
；
[0057][0058]
式中，m
c
为是热胀引起的合成力矩范围，n
·
m；fx为水平管线在x方向上所受的力，fx＝eε
x
a
x
，e为20℃时的弹性模数，ε
x
为水平管线在x方向上的应变，a
x
为水平管线在x方向受力面积，n；fy、fz分别为水平管线在与x方向垂直的y方向与z方向上所受的力，n，计算方法同fx；
[0059]
步骤102，将m
c
代入式(5)中进行计算，得到与l值对应的二次应力值σ
e
。
[0060][0061]
式中，σ
e
为管线热胀应力范围即二次应力，mpa；w为管线的截面抗弯矩，mm3，按计算，其中d1为管线外径，mm，d2为管线内径；i为应力增加系数，对于所述水平直管线，0.75i等于1；
[0062]
步骤103，将l值代入，计算不等式σ
e
≤f[1.2[σ]
20
+0.2[σ]
t
+([σ]
t
‑
σ
l
)]右侧的值，然后与上一步得到的σ
e
比较，判断是否满足不等式条件，若满足条件，则保留该l值的数据，否则舍弃该l值；
[0063]
式中，[σ]
20
为管线所用材料在20℃时的许用应力，mpa，取值查阅国家标准gb50316
‑
2000附录a可得；[σ]
t
为管线所用材料在设计温度t℃时的许用应力，根据设计温度t查阅国家标准gb50316
‑
2000附录a可得；f为应力范围减小系数，具体取值参见《中华人民共和国电力行业标准dl/t5366
‑
2006》19
‑
20页；
[0064]
一次应力σ
l
按下式(6)计算：
[0065][0066]
式中，p为管内工质设计压力，mpa；d1为管线外径，mm；d2为管线内径，mm；q为管线单位长度重力载荷，n/m；
[0067]
步骤104，将l值代入中进行计算，得到该l值所对应的成本值c；
[0068]
式中,c为成本值；c0为成本系数，与支吊架种类、单价及施工成本有关，可结合具体工程实际根据施工单位具体施工成本支出进行取值；l为管线的长度，l为相邻两个支吊架之间的间距，即表示一条管线所设置的支吊架总的个数。
[0069]
(c)逐渐减小第二步(a)中相邻的两个支吊架间距l，(如可以以步长0.1逐渐减小支吊架间距尺寸)，重复第二步(b)，进行迭代计算，直至l减小至负值，结束迭代计算；
[0070]
(d)将每个已保留的l值所对应的成本值c及σ
e
代入中计算，得到与每个已保留的l值所对应的价值v；
[0071]
式中，v为综合考虑二次应力σ
e
与成本c的加权价值；a为二次应力的权重系数；b为成本的权重系数，a、b值根据所述两个因素的重要程度进行赋值，a+b＝1；
[0072]
由于相邻两个支吊架的间距l值越小，理论上二次应力值σ
e
就越小，管线的力学性能就越满足要求。但是l值越小，整个管线所需要设置的支吊架个数越多，成本c越高，由此可见，相邻两个支吊架的间距l值并非越小越好，因此需要综合二次应力与成本这两个因素进行考虑。两者由于二次应力σ
e
和成本c的量纲不同，因此数值量的意义不同，不能直接进行比较，因此需要将上述两个量转化为无量纲的相对量。在进行寻优迭代的过程中，从第一步计算的l
max
开始每一个l值对应一个二次应力值σ
e
和一个成本值c。σ为求和符号，∑c是所有l值对应的成本求和，表示某个l值所对应的成本占总成本的比重，所占的比重越小表示成本越低、越好；同理。
[0073]
(e)在上述的所有支吊架间距l中选取使得v值最小的l值作为相邻两个支吊架的最佳间距；若所有l值下的二次应力均不满足上述不等式σ
e
≤f[1.2[σ]
20
+0.2[σ]
t
+([σ]
t
‑
σ
l
)]的要求，则根据设计经验更换步骤二中的基本参数(管线材质或调整设计压力p等)，然后返回到步骤三重新计算，直至取得支吊架最佳间距；
[0074]
步骤四、根据步骤三确定的支吊架间距尺寸及步骤二确定的基本尺寸利用solidworks建立管线及支吊架的三维模型，并将模型导入ansys软件中进行有限元仿真分析，输出仿真得到的支吊架能承受的最大应力及应变值，最后将输出的所述最大应力及应变值与管线在实际工作过程中能承受的极限应力及应变值比较，如果满足实际工作需求，则该支吊架模型合格，直接导出模型，根据所述模型进行实际安装即可；若不满足要求，则根据设计经验更换步骤二的基本参数(如：所述的管线材质或调整设计压力p等)，然后重复步骤三和步骤四，直到满足要求为止。