一种计算航空发动机常用圆柱滚子轴承抗偏斜角度的方法与流程

1.本发明涉及航空发动机圆柱滚子轴承设计技术领域，具体涉及一种计算航空发动机常用圆柱滚子轴承抗偏斜角度的方法。


背景技术：

2.圆柱滚子轴承是航空发动机转子系统的主要支撑部件，一般情况下，转子部件至少通过两个轴承支撑在静子部件上，轴承外圈装配在静子部件上，内环装配在转子部件上；对于中介轴承，内外套圈分别与航空发动机的高、低压转子相连接，内圈和外圈同时旋转；理论上，转子部件的中心与静子部件的中心是重合的，高压转子与低压转子的轴线是重合的。但是在实际装配过程中，由于零件的尺寸公差、行为公差等因素的影响，实际的转子、静子以及高低压转子轴线存在一定的夹角，轴承内外圈之间也会相应产生夹角。因此，在轴承设计过程中需要考虑轴承是否能够抵抗该偏斜夹角。
3.轴承偏斜角对航空发动机整机振动、轴承强度寿命和总体性能有着重要影响，如果设计轴承所能承受的偏斜能力小于实际轴线偏斜角度，则圆柱滚子轴承的滚动体与滚道将会发生应力集中，严重降低轴承寿命，进而带来一系列的问题、故障，甚至导致大的飞行事故。
4.目前，圆柱滚子轴承抗偏斜角计算没有统一的计算方法，一些教科书中只给出圆柱滚子轴承一般偏斜角不超过3
′
或4
′
的经验，没有提供计算方法。因此，遇到圆柱滚子轴承抗偏斜设计时的偏斜角问题无法快速有效的给出解决方案。
5.综上所述，现有的圆柱滚子轴承设计没有考虑抗偏斜能力问题，抗偏斜角计算没有计算方法，容易出现圆柱滚子轴承抵抗偏斜的能力与发动机实际产生的偏斜角度不匹配，导致圆柱滚子轴承发生局部应力集中，降低轴承寿命的问题。


技术实现要素：

6.本发明的目的是为了解决现有的圆柱滚子轴承设计没有考虑抗偏斜能力问题，抗偏斜角计算没有计算方法，容易出现圆柱滚子轴承抵抗偏斜的能力与发动机实际产生的偏斜角度不匹配，导致圆柱滚子轴承发生局部应力集中，降低轴承寿命的问题，进而提供一种计算航空发动机常用圆柱滚子轴承抗偏斜角度的方法。
7.本发明的技术方案是：
8.一种计算航空发动机常用圆柱滚子轴承抗偏斜角度的方法，所述方法是通过以下步骤实现的，
9.步骤一、计算圆柱滚子3的凸度半径r：
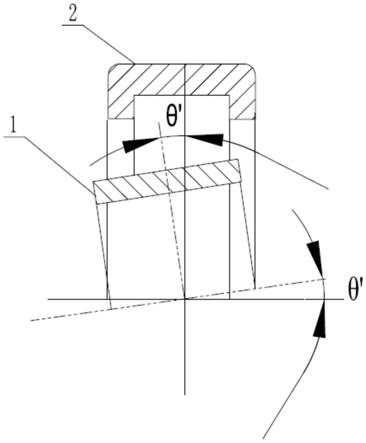
10.首先，明确圆柱滚子轴承内圈1与外圈2之间的偏斜最大角度要求，此时轴承内圈1与外圈2所在轴线偏斜的角度为θ'；
11.然后，明确圆柱滚子轴承中滚子的修形方式，当圆柱滚子轴承中圆柱滚子3的修形方式为平直段修形方式时，根据几何关系得到如下关系式：
[0012][0013]
进一步地，计算圆柱滚子3的凸度半径r，所述的圆柱滚子3的凸度半径r为：
[0014][0015]
其中，l为圆柱滚子3的长度，l
w
为圆柱滚子3平直段长度，δ为滚子凸度下沉量，r为滚子边缘倒角；
[0016]
步骤二、计算圆柱滚子轴承中内圈1的滚道有效长度l0：
[0017]
步骤三、确定偏斜角θ的计算边界：
[0018][0019]
步骤四、计算平直段修形圆柱滚子轴承偏斜角θ：
[0020]
结合步骤二和步骤三，平直段修形圆柱滚子轴承最大偏斜角θ计算公式为：
[0021][0022]
步骤五、验证平直段修形圆柱滚子轴承偏斜角θ：
[0023]
平直段修形圆柱滚子轴承偏斜角θ应满足：
[0024]
θ≤θ'
[0025]
当θ≤θ'时，平直段修形圆柱滚子轴承偏斜角是否满足偏斜最大角度要求。
[0026]
进一步地，步骤二中的滚道有效长度l0计算方式为：
[0027]
l0＝d
b
‑
2l3[0028]
其中，l0为内圈1的滚道有效长度，d
b
为内圈1的挡边6的距离，l3为内圈1的单侧越程槽尺寸。
[0029]
进一步地，步骤一中所述平直段修形方式的圆柱滚子3中心设有一段平直段，滚子边缘倒角与平直段之间为圆弧过渡，圆弧半径也称凸度半径r。
[0030]
进一步地，步骤二中所述的内圈滚道有效长度l0是指内圈滚道平直段的长度。
[0031]
进一步地，步骤三中所述的偏斜角θ的计算边界为圆柱滚子轴承中滚子边缘倒角r不能与内圈1的第一油沟4的油沟边缘a和第二油沟5的油沟边缘b发生接触的极限角度。
[0032]
本发明与现有技术相比具有以下效果：
[0033]
1、通过本发明提供的偏斜角计算公式，可以较为准确的计算出圆柱滚子轴承所能承受的偏斜角数值；
[0034]
2、本发明提供的偏斜角计算方法考虑了圆柱滚子的修形、行为公差和尺寸公差；
[0035]
3、本发明提供的偏斜角计算公式对于圆柱滚子轴承抗偏斜优化设计非常适用，可以有效查找影响偏斜角设计的有效因素，继而找到有效设计因素。
[0036]
4、本发明计算航空发动机圆柱滚子轴承抗偏斜角度的方法能够直观的推断出影响轴承抵抗偏斜能力的轴承内部设计因素，有滚道有效长度、滚子的凸度、滚子的直线段长度。
[0037]
5、本发明计算航空发动机圆柱滚子轴承抗偏斜角度的方法能够防止圆柱滚子轴
承抵抗偏斜的能力与发动机实际产生的偏斜角度不匹配，预防轴承发生局部应力集中，降低轴承寿命，为圆柱滚子轴承的合理设计提供必要的支撑。
附图说明
[0038]
图1是本发明的圆柱滚子轴承内外圈偏斜示意图；
[0039]
图2是本发明的带修形方式的圆柱滚子示意图；
[0040]
图3是本发明的圆柱滚子轴承内圈示意图；
[0041]
图4是本发明的局部带凸度的圆柱滚子与内圈组装示意图；
[0042]
图5是本发明的局部带凸度的圆柱滚子与内圈偏斜示意图；
[0043]
图6是本发明的圆柱滚子轴承偏斜角计算示意图。
具体实施方式
[0044]
具体实施方式一：结合图1至图6说明本实施方式，本实施方式的一种计算航空发动机常用圆柱滚子轴承抗偏斜角度的方法，所述方法是通过以下步骤实现的，
[0045]
步骤一、计算圆柱滚子3的凸度半径r：
[0046]
首先，明确圆柱滚子轴承内圈1与外圈2之间的偏斜最大角度要求，此时轴承内圈1与外圈2所在轴线偏斜的角度为θ'；
[0047]
然后，明确圆柱滚子轴承中滚子的修形方式，当圆柱滚子轴承中圆柱滚子3的修形方式为平直段修形方式时，根据几何关系得到如下关系式：
[0048][0049]
进一步地，计算圆柱滚子3的凸度半径r，所述的圆柱滚子3的凸度半径r为：
[0050][0051]
其中，l为圆柱滚子3的长度，l
w
为圆柱滚子3平直段长度，δ为滚子凸度下沉量，r为滚子边缘倒角；
[0052]
步骤二、计算圆柱滚子轴承中内圈1的滚道有效长度l0：
[0053]
步骤三、确定偏斜角θ的计算边界：
[0054][0055]
步骤四、计算平直段修形圆柱滚子轴承偏斜角θ：
[0056]
结合步骤二和步骤三，平直段修形圆柱滚子轴承最大偏斜角θ计算公式为：
[0057][0058]
步骤五、验证平直段修形圆柱滚子轴承偏斜角θ：
[0059]
平直段修形圆柱滚子轴承偏斜角θ应满足：
[0060]
θ≤θ'
[0061]
当θ≤θ'时，平直段修形圆柱滚子轴承偏斜角θ满足设计要求。
[0062]
图2和图6中的“o”代表为圆柱滚子凸度半径所在圆的圆心，图6中的“b”和“c”分别代表平直段圆柱滚子的平直段与凸度圆弧过渡的两个交点，b点为凸度圆弧与滚子圆角的过渡，e点为圆弧bc的中点。
[0063]
具体实施方式二：结合图3说明本实施方式，本实施方式的步骤二中的滚道有效长度l0计算方式为：
[0064]
l0＝d
b
‑
2l3[0065]
其中，l0为内圈1的滚道有效长度，d
b
为内圈1的挡边6的距离，l3为内圈1的单侧越程槽尺寸。其它组成和连接关系与具体实施方式一相同。
[0066]
具体实施方式三：结合图2和图6说明本实施方式，本实施方式的步骤一中所述平直段修形方式的圆柱滚子3中心设有一段平直段，滚子边缘倒角与平直段之间为圆弧过渡，圆弧半径也称凸度半径r。其它组成和连接关系与具体实施方式一或二相同。
[0067]
本实施方式的步骤一中所述平直段修形方式的滚子截面非矩形；滚子边缘倒角与平直段之间为大圆弧过渡。
[0068]
具体实施方式四：结合图3和图6说明本实施方式，本实施方式的步骤二中所述的内圈滚道有效长度l0是指内圈滚道平直段的长度。其它组成和连接关系与具体实施方式一、二或三相同。
[0069]
具体实施方式五：结合图2、图4、图5和图6说明本实施方式，本实施方式的步骤三中所述的偏斜角θ的计算边界为圆柱滚子轴承中滚子边缘倒角r不能与内圈1的第一油沟4的油沟边缘a和第二油沟5的油沟边缘b发生接触的极限角度。如此设置，滚子圆角与修正线过渡点不能与内圈滚道边缘位置接触，以免受载时，滚子与油沟接触，出现较大的应力集中。其它组成和连接关系与具体实施方式一、二、三或四相同。
[0070]
以上实施例仅用以说明本发明的技术方案，而非对其限制；尽管参照前述实施例对本发明进行了详细的说明，本领域的普通技术人员应当理解：其依然可以对前述各实施例所记载的技术方案进行修改，或者对其中部分技术特征进行等同替换；而这些修改或者替换，并不使相应技术方案的本质脱离本发明各实施例技术方案的精神和范围。