一种晶格扰动模式下晶体材料理想强度的高通量计算方法

本发明属于材料领域，具体涉及一种晶格扰动模式下晶体材料理想强度的高通量计算方法。

背景技术：

晶体材料是完全由晶体或大部分由晶体构成的工业材料。材料强度是指材料抵抗外界破坏的能力，用来表征材料在固定载荷下，随着应变增大直至发生破坏时的应力大小。衡量材料强度的物理量也有很多种，如抗拉强度、抗弯强度、抗剪切强度等。材料的理想强度对于塑性变形的响应明显与硬度不同，但根据塑性变形理论中的派纳模型中所表述的，晶体产生滑移的阻力与理想强度和剪切模量有着密切的关系，因此研究材料的理想强度在材料领域十分有意义。但是实验中合成和存在的晶体不可能是完美的，内部存在很多的缺陷，因此研究理想强度就存在一定的困难。基于密度泛函理论的第一性原理的计算方法解决了这一疑惑。

在基于密度泛函理论的第一性原理的计算方法中，将理想强度的常规计算方案被定义为无干扰方法，即将一个对称约束施加在一个原始的对称单元格上。相比之下，晶格扰动方法是为了打破对称约束，以实现基态相位，并在应力－应变计算过程中从鞍点任意移动原子。在晶格扰动方法中，为了让离子运动有更多的独立模式，γ点软模下的原胞或布里渊区其他点处软模下的超胞被采用。经检索发现，尽管用于传统理想强度计算的无扰动法已经得到了广泛的应用。但是在无扰动方法中，原始单元的对称约束可能导致晶格能量在势能面不稳定鞍点处的保持。因此采用扰动法来探索与声子相关的过早失稳是非常有必要，同时也是缺失的。此外，材料基因组计划(materialsgenomeinitiative)，简称mgi，是奥巴马于2011年6月24日颁布启动的“先进制造业伙伴关系”方案中至关重要的一部分，美国政府在对信息技术革命的深刻反省下，充分体会到材料技术的革新对于产业发展和经济发展的重要性。现在科技发展越战越勇，在科技潮流中快速发展的数据共享与计算工具的不断开发与利用对mgi的进步与发展有着重要的作用。

技术实现要素：

本发明公开了一种晶格扰动模式下晶体材料理想强度的高通量计算方法，该方法包含了运用高通量技术计算晶体材料在晶格扰动方法下的理想强度的方法，可以减少耗时、高成本的实验，大大缩短新材料研发周期，能够有效捕捉声子失稳的发生，从而筛选出具有优异力学性质的材料。该方法包括如下步骤：

本发明的一种晶格扰动模式下晶体材料理想强度的高通量系统，其包括有晶体结构选取模块、坐标系建立模块、加载外力模块和应力－应变曲线生成模块；

晶体结构选取模块用于生成被测对象的晶体四元组信息film(fa,fb,fc,fd)；

坐标系建立模块用于依据空间坐标系o-xyz获取被测对象的晶体四元组信息film(fa,fb,fc,fd)中的每一个原子坐标fd；

加载外力模块第一方面依据被测对象的空间坐标系o-xyz来选取力加载的方向和/或耦合方向；第二方面设置加载力的形式；第三方面设置加载力的大小；

三个方向分别是指o-xyz坐标系下的x轴方向、y轴方向和z轴方向；

四个耦合方向分别是指o-xyz坐标系下的x轴与y轴形成的耦合方向，记为x&y耦合；o-xyz坐标系下的x轴与z轴形成的耦合方向，记为x&z耦合；o-xyz坐标系下的y轴与z轴形成的耦合方向，记为y&z耦合；o-xyz坐标系下的三轴同时耦合，记为x,y&z耦合；

加载力的形式为拉伸变形和剪切变形；

被测对象的拉伸应变εtensile为

矩阵表示拉伸应变εtensile为

简单剪切和纯剪切的应变矩阵表示为

输出的纯剪切变形模式下的应变为

基于密度泛函理论的第一性原理得到能量－应变曲线为

拉伸变形和剪切变形依据的是gb/t228.1－2010标准；

应力－应变曲线生成模块用于在matlab软件中生成被测对象的力学性能参数，并以文件形式输出。

通常来说，这种通过扰动法计算的理想强度将更加接近于真实材料的强度，因为由于晶格对称性约束，传统非扰动理想强度计算方法很难捕捉声子失稳导致的材料力学失稳。因此通过无扰动法求解出的材料理想强度将远远大于通过扰动法求解出的材料的理想强度。为了强调两种方法求解理想强度结果出现偏离的物理起源，我们需要进一步探索与声子有关的性质，因为这种与声子有关的性质与扰动法息息相关。

根据晶格动力学理论，非扰动模式和扰动模式之间的联系可以由特定声子软模的本征向量构成，因为声子软模会降低晶体的能量，使结构发生相变。因此，在变形过程中施加一系列不同应变时，我们可以得到变化的声子色散曲线，以确定声子失稳时的临界应变，从而更好的衡量材料的真实理想强度。在大多数下，过早的声子失稳会降低材料的理想强度和柔韧性。

基于材料结构库，进行高通量搜索，计算不同结构不同方向的理想强度，建立材料力学性质结构库，并筛选出增加随机扰动情况下具有最高理想强度的材料，这样的材料强度预测有利于提供给实验合理的指导。

基于材料结构库，进行高通量搜索，计算不同结构不同方向的理想强度，建立材料力学性质结构库，并筛选出增加随机扰动情况下具有最高理想强度的材料，这样的材料强度预测有利于提供给实验合理的指导。与传统方法相比达到的优点在于：

①本发明方法包含构建增加原子随机扰动情况下的材料体系。

②利用高通量技术实现了计算原子随机扰动情况下对晶体任意方向的理想强度，经扰动法计算的理想强度更接近于实际材料的强度，这对于更好的衡量材料的力学性能是必不可少的。

③本发明方法能够筛选具有优异的力学性能的二维或者三维材料，对强固体材料设计具有指导意义。

附图说明

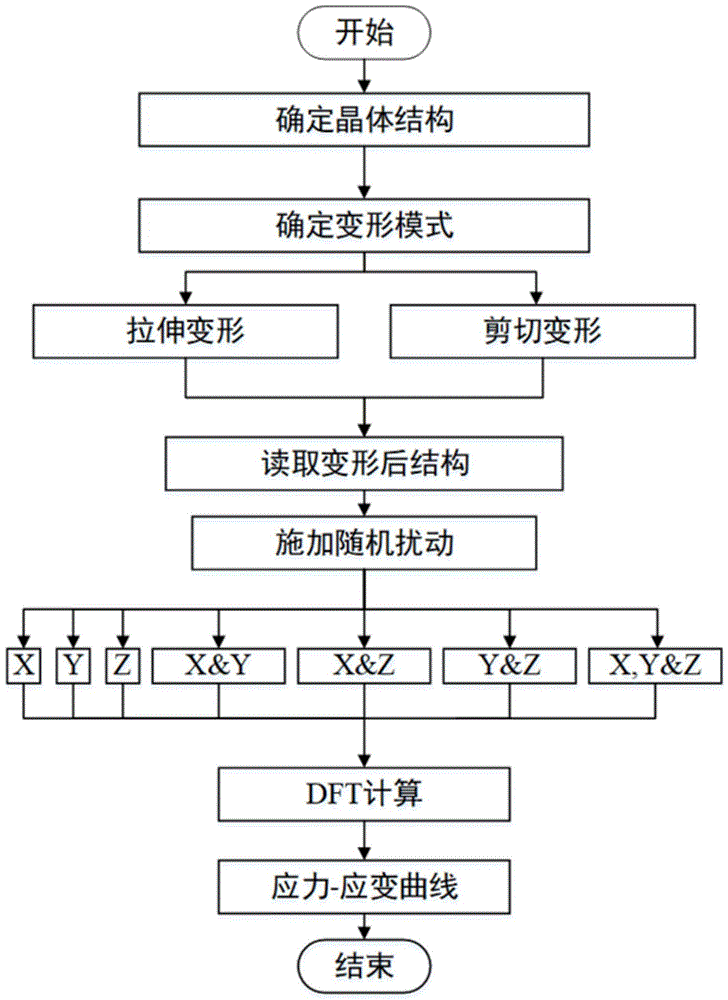
图1是本发明晶格扰动模式下晶体材料理想强度的高通量计算方法流程图。

图2是本发明中被测对象的示意图。

图2a是金刚石的晶体结构图。

图3a是理想条件下的晶体结构图。

图3b是经过随机扰动后的晶体结构图。

图4是测试时间里外力加载的过程图。

具体实施方式

下面将结合附图对本发明做进一步的详细说明。

为了实现在晶格扰动模式下进行晶体材料理想强度的计算，本发明采用在win7操作系统下，在matlab(版本号7.13)平台并结合atomsk软件上进行晶格扰动仿真建模，得到了一种晶格扰动模式下晶体材料理想强度的高通量计算系统，将晶格扰动模式下晶体材料理想强度的高通量计算系统简称为ldm(latticedisturbancemodel)模型。用atomsk软件给被测对象提供加载外力f加载使晶体结构扰动。本发明ldm模型通过采用高通量计算，可以减少耗时、高成本的实验，大大缩短新材料研发周期，对材料基因组计划(mgi)的进步与发展有着重要的作用。

高通量计算是整合了材料设计过程中的数据、代码、计算工具等以实现共享，从而加速新材料的研发。

参见图2a所示的金刚石的晶体结构图，这是传统材料学科中最常见的。参见图2所示，以一个正立方体代表一个被测对象(即晶体结构)的外形。正立方体的中心点代表晶体结构的质心点o，建立被测对象坐标系，记为o-xyz。

本发明的ldm模型通过对不同晶体结构进行晶格扰动加载，分别从三个方向和四个耦合方向加载外力f加载，计算晶体结构的应力－应变曲线，以应力－应变曲线体现被测对象的材料强度性能。

三个方向分别是指o-xyz坐标系下的x轴方向、y轴方向和z轴方向。

四个耦合方向分别是指o-xyz坐标系下的x轴与y轴形成的耦合方向，记为x&y耦合；o-xyz坐标系下的x轴与z轴形成的耦合方向，记为x&z耦合；o-xyz坐标系下的y轴与z轴形成的耦合方向，记为y&z耦合；o-xyz坐标系下的三轴同时耦合，记为x,y&z耦合。

本发明研究的晶体材料的理想强度是零温度下理想无缺陷晶体在均匀变形下可达到的最大应力，在微观上被理解为理想晶体在较大应变下晶体内化学键的断裂。原理想晶体结构与经过随机扰动处理的晶体结构对比，如图3a、图3b所示。本发明是在图3a形式的晶体结构进行的ldm模型处理。

本发明的一种晶格扰动模式下晶体材料理想强度的高通量计算系统(ldm)包括有晶体结构选取模块、坐标系建立模块、加载外力模块和应力－应变曲线生成模块。

晶体结构选取模块

在本发明中，晶体结构选取模块用于生成被测对象的晶体四元组信息film(fa,fb,fc,fd)；

fa代表晶格基矢；

fb代表原子种类；

fc代表原子个数；

fd代表原子坐标，即fd(x,y)。如图2a中，晶体结构中的每一个原子在空间坐标系为o-xyz下的坐标值都是已知值。

坐标系建立模块

在本发明中，坐标系建立模块用于依据被测对象的空间坐标系o-xyz获取晶体四元组信息film(fa,fb,fc,fd)中的每一个原子坐标fd；

加载外力模块

在本发明中，加载外力模块第一方面依据被测对象的空间坐标系o-xyz来选取力加载的耦合方向；第二方面设置加载力的形式；第三方面设置加载力的大小；

加载力的形式为拉伸变形和剪切变形。

在本发明中，拉伸变形和剪切变形依据的是gb/t228.1－2010标准，《金属材料拉伸试验》。

应力－应变曲线生成模块

在本发明中，应力－应变曲线生成模块用于在matlab软件中生成被测对象的力学性能参数，并文件形式输出。

在本发明中，应力－应变曲线生成模块输出的文件能够应用于材料基因组计划(mgi)。

参见图1所示，本发明的一种晶格扰动模式下晶体材料理想强度的高通量计算方法，包括有下列步骤：

第一步：选取被测对象的晶体结构；

在本发明中，被测对象是从晶体结构文件中选取的。晶体结构文件中至少包含有晶格基矢、原子种类、原子个数、原子坐标的信息。晶体结构文件，记为film，所述film包含的晶体信息称为晶体四元组信息，记为film(fa,fb,fc,fd)，其中，fa代表晶格基矢，fb代表原子种类，fc代表原子个数，fd代表原子坐标。

参见图2所示，以一个正立方体代表一个晶体结构的外形。正立方体的中心点代表晶体结构的质心点o，建立被测对象坐标系，记为o-xyz。

第二步：确定晶体的变形方式和变形结构；

通常来说，被测对象在进行各向异性材料理想强度计算时，晶体的变形模式分为拉伸变形和剪切变形两种模式。

对于拉伸变形，首先通过使拉伸晶体学方向平行于一个直角坐标轴以确保单轴应力状态来进行拉伸变形的投影过程。

而对于剪切变形来说，通过使剪切面垂直于一个笛卡尔轴，同时保持剪切方向沿另一个笛卡尔轴来进行剪切变形过程，然后通过affine变形向晶体施加应变。

在本发明中，在被测对象坐标系o-xyz中，晶胞上沿某一方向施加一组递增的应变，而在垂直于该方向上晶格和原子位置完全驰豫，直至共轭应力分量(即hellmann–feynman应力)达到0.1gpa。此时被测对象的拉伸应变εtensile为：

a0表示平衡条件下被测对象的晶格常数。

a表示应变条件下被测对象的晶格常数。

在本发明中，为了更好地表示施加应变的方向(如图1所示)，采用矩阵表示拉伸应变εtensile为：

εx表示被测对象坐标系o-xyz中x轴方向的拉伸应变分量。

εy表示被测对象坐标系o-xyz中y轴方向的拉伸应变分量。

εz表示被测对象坐标系o-xyz中z轴方向的拉伸应变分量。

在本发明中，而对于剪切变形，通过使剪切面垂直于其中一个直角坐标轴来进行投影过程，同时保持其剪切方向沿另一个坐标轴方向。主要包含两种不同的剪切模式，即简单剪切(simpleshear)和纯剪切(pureshear)。在简单剪切变形模式下，沿一个直角坐标系轴为每个原子平面引入平行位移，而对于纯剪切，在两个正交直角坐标系轴之间施加等幅的对称位移。

简单剪切和纯剪切的应变矩阵表示为：

εsimple表示简单剪切变形模式下的应变。

εxy表示在被测对象坐标系o-xyz的x&y耦合方向发生剪切的剪切应变分量。

εxz表示在被测对象坐标系o-xyz的x&z耦合方向发生剪切的剪切应变分量。

εyz表示在被测对象坐标系o-xyz的y&z耦合方向发生剪切的剪切应变分量。

应用本发明ldm模型后，输出的纯剪切变形模式下的应变为：

εpure表示纯剪切变形模式下的应变。

被测对象经加载外力模块后，即在晶体结构被选择拉伸或者剪切变形后，如图3b所示，通过矩阵运算实现均匀(affine)变形。在均匀变形过程中，将均匀增加的应变连续应用于平衡状态下的晶格，可得到一系列在测试时间t里被施加不同应变的晶体结构信息，记为csv＝{csv0,csv1,csv2,…,csvq,…,csvq}，如图4所示。csv0为初始时的晶体结构信息，csv1为在第一个测试时间时的晶体结构信息，csv2为在第二个测试时间时的晶体结构信息，csvq为在第q个测试时间时的晶体结构信息，csvq为在测试时间结束时的晶体结构信息。

在本发明中，被测对象的当前晶体结构信息，记为csvold。被测对象的当前晶体结构信息csvold经纯剪切变形模式下的应变后，提取得到的新的晶体结构信息为csvnew。所述csvold转换成所述csvnew采用了离散傅里叶变换(discretefouriertransform，dft)的处理手段。

第三步：对变形后的原子结构施加随机扰动；

在得到系列被施加不同应变的晶体结构信息csv＝{csv0,csv1,csv2,…,csvq,…,csvq}后，直接进行基于密度泛函理论的第一性原理的计算方法为无扰动法。但是为了能够更加准确地计算材料的理想强度，在开始计算材料的理想强度前，需要对晶体施加随机扰动。采用atomsk软件对晶体结构信息csv＝{csv0,csv1,csv2,…,csvq,…,csvq}施加随机扰动，通过沿x轴，y轴或z轴方向，x轴和y轴耦合方向，x轴和z轴耦合方向，y轴和z轴耦合方向以及x轴，y轴和z轴耦合方向施加不同的随机位移来扰乱原子坐标fd(x,y)，原子坐标fd(x,y)扰动前后参考图3a和图3b所示，产生一系列新的晶体结构信息来进行接下来的理想强度计算。经过理论验证和比较，对晶体结构施加随机扰动时，使原子移动最为合适。当原子移动的实际范围大于时，会显示原子位置过近的错误，但是当原子移动小于时，计算显示结果和没有施加随机扰动时情况一致，这说明扰动对于晶体结构的影响甚微。

第四步：理想强度计算；

在本发明中，通过密度泛函理论计算得到材料在不同应变下的应力，绘制不同晶体结构方向的应力－应变关系曲线，得到不同方向的拉伸和剪切强度，并比较沿典型晶体学方向或滑移系统的各向异性理想抗拉强度或抗剪强度，然后求出理想抗拉强度σmin和理想抗剪强度τmin的最小值。

在实际计算模拟过程中，要确定理想强度，就必须要计算材料的应力－应变关系曲线。在通过基于密度泛函理论的第一性原理得到能量－应变曲线后，通过进一步采用公式(5)处理，即可得到应力－应变的关系曲线。

σ表示应力。

表示求导符号。

e表示晶体结构具有的能量。

v(ε)表示晶体结构在应变ε下的体积。应变ε分别表示公式(2)、公式(3)和公式(4)中的应变。则有：

在应力－应变曲线中，当应力达到第一个峰值时，晶体结构开始失稳，对应的应力为理想强度，对应的应变为临界(或极限)应变；当应变大于临界应变时，材料将发生变形失稳断裂。

在得到一系列被施加扰动后的晶体结构信息后，通过旋转晶体结构计算不同方向的拉伸和剪切强度。均匀变形下的理想强度对应于应力-应变曲线的临界应力，在该临界应力下，无缺陷的晶体变得不稳定，从而限定了晶体可达到的强度上限。因此，首先确定并比较沿典型晶体学方向或滑移系统的各向异性理想抗拉强度或抗剪强度，然后求出理想最小值抗拉强度σmin和理想最小值抗剪强度τmin。

其中抗拉强度σmin和抗剪强度τmin如下：

σmin＝min{σ<hkl>}(6)

τmin＝min{τ{uvw}<hkl>}(7)

<hkl>表示结晶方向。

{uvw}表示滑动面。

在本发明中，更高的抗拉强度和抗剪强度表示材料对断裂或剪切引起的晶格不稳定性具有较高的抵抗力，可能具有较高的强度。

通常来说，这种通过扰动法计算的理想强度将更加接近于真实材料的强度，因为由于晶格对称性约束，传统非扰动理想强度计算方法很难捕捉声子失稳导致的材料力学失稳。因此通过无扰动法求解出的材料理想强度将远远大于通过扰动法求解出的材料的理想强度。为了强调两种方法求解理想强度结果出现偏离的物理起源，我们需要进一步探索与声子有关的性质，因为这种与声子有关的性质与扰动法息息相关。

根据晶格动力学理论，非扰动模式和扰动模式之间的联系可以由特定声子软模的本征向量构成，因为声子软模会降低晶体的能量，使结构发生相变。因此，在变形过程中施加一系列不同应变时，可以得到变化的声子色散曲线，以确定声子失稳时的临界应变，从而更好的衡量材料的真实理想强度。在大多数下，过早的声子失稳会降低材料的理想强度和柔韧性。

基于材料结构库，进行高通量搜索，计算不同结构不同方向的理想强度，建立材料力学性质结构库，并筛选出增加随机扰动情况下具有最高理想强度的材料，这样的材料强度预测有利于提供给实验合理的依据。