基于多源流形嵌入迁移的脑电信号分类方法

1.本发明属于模式识别领域，是一种针对运动想象脑电信号利用其它对象的有标签脑电数据对目标对象的无标签脑电数据进行迁移分类的方法。


背景技术：

2.脑机接口技术(bci)是一种不依赖于人体神经和肌肉组织的正常传输通路，而直接进行人脑与外界之间信息交流的人机交互系统，对于活动能力缺失患者的能力恢复和功能训练具有重要意义，可以为意识障碍和中风患者的康复提供很大的帮助。患者可以通过该技术实现机械设备的控制，完成所需的动作。脑电信号(eeg)由于无需手术、使用方便的优点是bci系统中使用最为广泛的信号。
3.基于eeg的bci系统已经取得了相当多的进展并应用于各个领域，但是考虑到eeg信号的特点：不平稳性、个体差异性问题，基于mi
‑
eeg的应用仍需要在使用前进行一定时间的校准阶段，为的是获取足够的标记数据，来训练特定于受试者的算法模型。然而就算是同一受试者，不同时间如上午和下午的eeg信号仍存在相当大的差异，如果在每次使用前都需要枯燥费时的校验阶段无疑为bci的交互增加了负担，利用迁移学习来克服现有研究的不足，在减少校准时间的同时，将模型的精度保持在一定的范围内，这无论是对bci系统的使用者还是研究者都具有重要的意义。
4.在bci系统中的迁移学习是将同一对象不同阶段的eeg信号进行迁移，或是不同对象的eeg信号进行迁移，迁移学习在bci领域的研究正在受到越来越多的关注，因为它能够解决应用中的痛点。迁移学习的概念分为源域和目标域，源域是指从某一个区域获取知识，而目标域是使用源域获取的知识来解决目标域中的任务。
5.现在大多数应用于bci系统的迁移方法都是基于特征迁移的，这是因为eeg信号中的特征提取是尤为关键的一步，已有的效果较好特征提取方法都是有监督的，而且需要较多的训练数据，与特征结合的迁移方法能够在迁移的同时提取信号的特征，能够有效提高迁移的效果。原始的eeg样本信号是通道乘采样点数的二维矩阵，协方差矩阵可以看作是初步的特征，而且协方差矩阵具有许多优点：协方差矩阵是对称正定矩阵并且位于黎曼空间上，而不是欧氏空间中，随着黎曼空间的方法在基于eeg的脑
‑
机接口中变得流行，最近也提出了许多基于特征的迁移方法。li考虑协方差的迁移，其中来自其它受试者的数据根据重要性抽样交叉验证进行加权，然后使用权重较高的部分来估计最终的预测函数。zanini等人提出了一种黎曼对齐ra方法。该方法利用其它受试者的参考协方差矩阵，对齐特定受试者的eeg协方差矩，ra首先计算源域中一些休息状态下试验的协方差矩阵，该状态下受试者不执行任何任务，然后计算其黎曼均值，下一步将用作参考矩阵，以减少对象/阶段间的变化，在运动想象中，休息状态时对象不执行任何任务的时间窗口。zanini改进的黎曼均值最小距离mdrm分类器，并证明了ra和改进的mdrm在分类中的有效性。
6.虽然ra在bci系统中成功应用黎曼几何来进行迁移，但仍有一些限制：ra对齐黎曼空间中的协方差矩阵，因此需要黎曼空间分类器，而这样的分类器很少，ra使用协方差矩阵
的黎曼均值，这是一个耗时的计算，特别是当eeg通道的数量很大时，ra用于事件相关电位分类需要在目标域中进行一些带标签的试验，因此当这些信息不可用时不能使用。为了解决这些问题，he等人提出了一种欧式对齐ea方法，在欧式空间中对齐来自不同对象的eeg试验，使它们更加一致。对于源域样本协方差矩阵，ea计算每个域的参考矩阵：所有协方差矩阵的算术平均值，然后用进行对齐。在ea之后，所有域的平均协方差矩阵变为单位矩阵。欧几里德空间和黎曼空间的特征提取和分类方法都可以应用到中，由于ea中的计算更灵活，并且对齐后可以使用欧几里德和黎曼空间分类器。he和wu证明了在离线和模拟在线的应用中ea在运动想象和事件相关电位分类方面更优于ra。
7.然而ea仅对齐了边缘分布，没有考虑条件分布以及分类器的约束，类与类之间的分布没有对齐，因此可以利用联合分布对齐来对特征样本进行迁移，本发明提出了基于多源流形嵌入迁移的脑电信号分类方法。


技术实现要素：

8.针对脑电信号中个体差异性大、校验时间长的问题，本发明提出了一种基于多源流形嵌入迁移的脑电信号分类方法(mmet)，并基于方法完成脑电信号分类。
9.本发明包括以下步骤：
10.步骤(1)：多通道脑电信号采集并进行预处理。采集源域受试者有标签和目标域受试者的无标签多通道运动想象脑电信号；接着利用带通滤波器对脑电信号进行8～35hz的低通滤波，用于脑电信号特征迁移。
11.步骤(2)：提取协方差特征，最小化源域和目标域特征的kl距离得到线性变换对源域样本协方差特征进行边缘分布对齐。
12.步骤(3)：对迁移后的样本协方差矩阵提取切线空间特征。
13.步骤(4)：对源域样本和目标域样本进行联合分布对齐(jda)。
14.步骤(5)：利用最小化结构风险准则(srm)对迁移后的源域样本训练域不变分类器，对目标域样本进行分类得到测试结果。
15.本发明的有益效果：传统的bci系统在使用前需要用户一段时间的训练时间来获取有标签的训练样本，而引入迁移学习后则可以有效减少训练时间甚至去除训练阶段。本发明基于流形学习，首先在流形空间对源域和目标域样本进行边缘分布对齐，然后利用切线空间特征获取样本的向量形式，最后利用流形映射和联合分布对齐在最小化风险准则下训练域不变分类器。本发明能够使用其它受试者的数据在目标用户无训练数据的情况下完成迁移分类。
附图说明
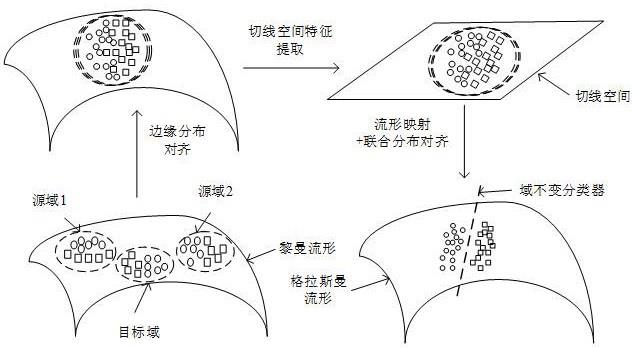
16.图1为本发明方法的流程图；
17.图2为数据集1受试5的迁移前和迁移后的特征分布图；
18.图3为数据集iia受试3的迁移前和迁移后的特征分布图；
19.图4为数据集1各个迁移成分对准确率的影响；
20.图5为数据集2各个迁移成分对准确率的影响。
具体实施方式
21.下面结合附图详细描述本发明基于多源流形嵌入迁移的脑电信号分类方法。如图1，本发明方法的实施主要包括5个步骤：(1)获取源域受试者的有标签和目标受试者无标签的脑电信号(2)提取信号协方差特征后利用线性变化对齐两域边缘分布(3)将对齐后的协方差矩阵提取切线空间特征(4)对齐源域和目标域特征的联合分布(5)利用经验风险最小化训练域不变分类器对目标域样本进行分类。
22.下面逐一对各步骤进行详细说明。
23.步骤(1)：本实施例选用bci竞赛公开数据，数据按照以下方式进行采集。bci competition iii dataset 1：该数据集包含7名受试者的eeg信号，每位受试者进行三类运动想象任务，要求在视觉提示后想象左手、右手或足的运动，每次实验持续3.5秒，均使用59个电极进行记录，电极位置采用国际10/20系统。每个受试者进行每类100组试验共200组实验，该数据集原始采样频率为1000hz，仅使用左手和右脚两类数据。bci competition iv dataset iia：该数据集包含9名受试者的eeg信号，每位受试者(编号c1
‑
c9)进行四类运动想象任务，要求在视觉提示后想象左手、右手、右足还有舌头的运动，每次实验持续4秒。所有实验均使用22个电极记录，电极位置采用国际10/20系统。训练集和测试集分别包含288组实验数据，该数据集原始采样频率为1000hz，本实验只选择其中的左手和右手的eeg信号进行测试，训练集和测试集都包含72组实验。本发明的迁移方法是基于多源域的，所以在数据集中其它所有受试者的有标签数据都会用来当做源域数据。
24.数据预处理：对所有的数据集进行相同的预处理步骤。每位受试者分别选择在视觉提示后的3s时间窗内提取受试者的运动想象脑电信号数据，然后利用5阶的巴特沃斯滤波器对数据进行8～30hz的带通滤波处理以滤除不相关的低频噪声。
25.步骤(2)：设k个通道的脑电样本信号为其协方差矩阵c为：c＝xx
t
，令a为线性变换矩阵，则变换后的eeg样本矩阵为变换后的协方差矩阵为：
[0026][0027]
利用kl距离来衡量源域和目标域的特征分布差异。令n
s
(0,c
s
)为源域特征的平均分布，c
s
为整个源域样本的平均协方差，n(0,a
t
c
s
a)为目标域特征的平均分布，c
t
为整个目标域样本的平均协方差，需要求解的线性变换矩阵a使得c
s
与c
t
间的kl距离尽可能的小，则相应的最优化函数为：
[0028][0029]
对其微分并等于零可得：
[0030][0031]
求得线性变换矩阵a的解为：
[0032][0033]
步骤(3)：将对齐后的源域协方差矩阵和目标协方差矩阵提取切线特征：
[0034]
x
i
＝upper(p
‑
1/2
log
p
(p
i
)p
‑
1/2
)
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(5)
[0035]
其中，upper(
·
)是拉直对称矩阵的上三角操作，p为切空间中任意一点，p
i
为对称正定矩阵。则映射后的源域向量和目标域向量分别为：
[0036][0037]
通过切线空间映射，可以获得新的特征矩阵以及
[0038]
步骤(4)：对源域样本和目标域样本进行联合分布对齐。在步骤2中仅对齐了边缘分布，但是类与类之间的分布差异没有考虑，因此考虑对齐源域和目标域的联合分布。
[0039][0040]
其中d
f
(p
s
,p
t
)表示源域特征p
s
和目标域特征p
t
间的边缘分布对齐，表示第c类的源域特征q
s
和目标域特征q
t
的条件分布对齐。
[0041]
步骤(5)：利用最小化风险准则对迁移后的源域样本训练域不变分类器。最小化风险准则是用来对分类器进行约束，结合对齐后的特征和条件分布项，总的目标函数服从以下表达：
[0042][0043]
其中f表示分类器，l(
·
)表示分类器与标签的损失项，g(
·
)为gmap流形映射项，||f||2为正则项分类器的范数平方，d
f
(d
s
,d
t
)为联合分布对齐项，α和γ分别表示正则化参数。y表示标签矩阵，k为核函数，tr(
·
)表示迹，h为对角指示矩阵，m0和m
c
为mmd矩阵,β即为所求的系数矩阵。
[0044]
对分类器f微分并等于零，可得最终解为：
[0045]
β＝((h+γm0+γm
c
)k+αi)
‑1ay
t
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(9)
[0046]
为了验证多源流形嵌入迁移算法在eeg信号分类中的性能，实验部分将本发明与ra
‑
mdrm、csp
‑
lda和ea
‑
csp
‑
lda方法在bci竞赛iv dataset 2a以及bci竞赛iii dataset 1的数据进行性能比较，通过测试分类精度来衡量本发明在脑电信号分类领域的可行性。
[0047]
表1给出了所提方法与其它三种方法在两个bci竞赛数据上的准确率对比。从表1可以看出，本算法在两个数据集上分别取得了83.14％和76.77％最高的平均准确率。在数据集dataset 1中，除了受试者2，其余受试者均比其它三种方法的准确率高，而且可以看到相比没有迁移的csp
‑
lda方法，其它三种迁移方法均取得了一个不错的准确率提升，这可能说明在此数据集中的受试者个体差异性大，迁移的方法能够有效解决特征分布差异的问题从而提高准确率。csp
‑
lda方法中受试者1、3、4、6、7的准确率均在50％左右，这近乎于一种猜测的结果，这说明在未迁移的情况下，依靠他人的训练数据是完全不能用来帮助目标受试者的，而经过本算法迁移后，除了受试者2，其余所有对象的准确率均大于80％，受试者5达到了93％的测试准确率，七个受试者的平均准确率更是提高了接近30％，说明了迁移方法的有效性。
[0048]
相比于其它两种迁移方法，本方法也展现出了优越性，平均准确率相比ra
‑
mdrm方法提高了约13.9％，比ea
‑
csp
‑
lda提高了约3.4％。在数据集dataset iia中，本方法也取得了最高的平均准确率，但受试者2、5、9的准确率略低于另两种迁移方法。而且相比于上个数
据集，本数据集的迁移方法提升没有那么明显，这可能说明本数据集中的数据特征分布更为相似，但每个受试者的平均准确率均是由迁移方法取得，这也说明了迁移的必要性。同时本方法的平均准确率相比于另两种迁移方法分别提升了约5.8％和2.4％。
[0049]
表1四种方法在两个bci数据集上的分类准确率
[0050][0051]
为了进一步验证迁移方法的有效性，同时形象的展现出迁移方法的效果，本小结对迁移前后的特征分布进行了特征可视化。这里使用了t分布随机邻域嵌入技术对迁移后的特征进行特征降维及数据可视化，t
‑
sne能够将高维数据降到2
‑
3维，降维后的特征就可以形象化的展现特征的分布情况。图2为数据集1中受试5的迁移前和迁移后的特征分布图；图3为数据集iia中受试3的迁移前和迁移后的特征分布图。特征图中圆圈和星号表示源域对象和目标域对象的第一类特征，叉叉和小点表示源域对象和目标域对象的第二类特征。理想的情况是属于同一类的圆圈和星号分布在一起，属于另一类的叉叉和小点分布在一起，这样就能够用源域对象训练的分类器来对目标对象进行分类。从图2中可以看到，迁移前源域和目标域的两类特征聚簇在一起，同时可以近似的看出源域特征形成了六团聚簇，分别对应着源域六个对象的特征，这说明不同对象间的个体差异性很大，因此不能直接用其它对象的数据分类目标对象。迁移后的特征分布图可以明显的看到源域的每类特征和目标域的每类特征分布更加接近，也就是圆圈和星号聚簇在一起，叉叉和小点聚簇在一起，达到特征迁移的目的。在图3中迁移前的特征分布明显没有上个数据集迁移前的独立的聚簇多，基本上都是分布在一大块区域，这也解释了为什么在数据集1上的迁移效果更好。在迁移后源域的每类特征分布和目标域的每类特征分布基本相似，达到了理想的迁移效果，有效的证明了本方法的实际性能。
[0052]
图4和图5分别为算法目标函数中每个成分：流形特征项gmap、结构化风险项srm和
联合分布对齐项jda对于两个数据集的每个受试者测试准确率的影响。可以看到由于数据集1的个体差异性大，图4中联合分布对齐项jda在加入后对算法性能的影响比较明显，受试者1、3、4、6在加入jda项后性能提升比较大，这可能说明当源域和目标域数据分布差别很大时，引入迁移成分能够有效的提高分类准确率。在图5中srm项的影响比较大，可以看到在加入srm后除了受试者2和受试者5其它受试者都有一个相当明显的效果提升，srm是用来规避分类器的误差风险，说明仅仅迁移是不够的，结合分类器的迁移可能会对准确率有一定的提升效果。
[0053]
综上，本发明提出了一种基于多源流形嵌入迁移的脑电信号分类方法，通过多个源域来让样本数据表达充分，利用流形学习首先对齐源域和目标域的边缘分布，然后提取切线特征获得特征的向量表示，最后根据联合分布对齐以及经验风险最小化原则训练一个域不变分类器，利用其它对象的有标签数据即可对目标对象的无标签数据进行迁移分类，有效的解决了个体差异性的问题同时减少了受试者长时间枯燥的训练时间，为bci的应用提供参考。