一种人工湿地生物堵塞的计算方法

本发明属于环境工程污水生态净化技术领域，尤其涉及一种人工湿地生物堵塞的计算方法。

背景技术：

人工湿地(cw，constructedwetland)堵塞是限制其高效、长效运行的瓶颈问题，会缩短人工湿地寿命、增加管理维护成本。相较于进水悬浮物引起的物理堵塞、填料孔隙间发生化学反应产生胶体或沉淀引起的化学堵塞，人工湿地中的生物堵塞更具普遍性，其后果也更为严重，是cw长效运行的主要限制因素。即使采取进水预处理、基质级配优化、植物优选配置及运行管理优化等预防措施，仍无法避免人工湿地生物堵塞。

而目前对于人工湿地生物堵塞的监测一般基于潜流湿地堵塞区的电阻率较未堵塞区低的特征，利用电阻率的大小判断判断潜流人工湿地的堵塞位点和堵塞程度。但是操作较为复杂，需要在湿地中插入多个电极，并额外提供电源，有的还需要排空水体后一定时间内完成测定。虽然一定程度上提高了生物堵塞的堵塞位置，但过程复杂，而且电极等都需要预先填埋进去,且没有预测功能。

目前鲜见关于人工湿地生物堵塞预测时间计算方法的报道。

技术实现要素：

发明目的：本发明的技术目的是针对人工湿地生物堵塞时间预测计算缺乏的问题，结合流体动力学的一些简单易得的参数，如填料粒径、进水特征等，建立了参数有效的生物堵塞模型。该模型可以动态描述生物堵塞的全过程，并且可以随着运行时间的增加而定量地预测在孔中积累的生物膜的质量，为预测生物堵塞提供了基础。结果说明了如何通过改变bod(biochemicaloxygendemand，生化需氧量)加载速率来影响堵塞，并预测生物膜在基质中的积累，从而进一步延长人工湿地的寿命。本发明为预测生物堵塞提供了方法，具有一定的实际运用价值。

技术方案：为了实现上述技术目的，本发明提供了一种垂直流人工湿地生物堵塞预测的具体计算方法，包括：

步骤1，设定计算的假定条件；

步骤2，计算与人工湿地生物堵塞预测相关的参数。

步骤1包括：设定如下计算的假定条件：忽略水流剪切力作用；忽略植物根系对水流的影响；不区别考虑微生物活的细胞和胞外聚合物，设置生物膜密度，一般取生物膜密度为1.05。

步骤2包括：

步骤2-1，计算孔隙流速；

步骤2-2，计算累计生物膜量；

步骤2-3，计算得到与人工湿地生物堵塞预测相关的参数。

步骤2-1包括：设定人工湿地中j时刻时一空间点处一点的渗透系数为ki,j，根据其水力梯度i及初始孔隙率n0计算出该点的孔隙流速ui,j。

步骤2-1中，根据如下公式计算孔隙流速：

ui,j＝ki,j·ii,j/ni,j

其中，ii,j是水力梯度，ki,j和ni,j分别为j时刻第i层的渗透系数和孔隙率。

步骤2-2包括：根据生物膜累计系数计算公式，设定在微元单位内生物膜浓度为一常数，结合生物膜浓度公式求得浓度c’i,j，进而求出累计生物膜量σi,j。

步骤2-2中，所述生物膜累计系数计算公式如下：

其中，l是柱深(长度)，c是流出的bod浓度，c0是流入的bod浓度，u是由步骤2-1中计算得出的孔隙流速。

步骤2-2中，所述生物膜浓度公式如下：

式中，xi与xi-1表示相邻两空间点同一时刻的坐标。ui-1,j为j时刻位于空间点i(第i层)前一个空间点i-1处(第i-1层)的孔隙流速；c'i-1,j为j时刻位于空间点i(第i层)前一个空间点i-1处(第i-1层)的生物膜浓度。

步骤2-2中，所述累计生物膜量σi,j通过下述公式计算：

式中，c’i,j为内部不同层的bod浓度，λ为生物膜累计系数，δt为时间间隔。

步骤2-3包括：

步骤2-3-1，根据累计生物膜量σi,j引起的孔隙率的变化，求得孔隙率ni,j+1；

其中，n0为初始孔隙率，σi,j为i层、j时刻的累计生物膜量，ρs为生物膜的密度；

步骤2-3-2，基于随孔隙率改变的kozeny-carman的方程k表示渗透系数，将时间步长为j的渗透系数ki,j更新为时间步长为j+1的渗透系数ki,j+1，如此循环直至j>jmax，如下公式所示：

其中，为多孔介质孔隙率，c和s分别kozeny-carman常数和比表面积；

步骤2-3-3，根据如下公式计算得到流量qi,j：

qi,j＝ui,j·ni,j·a

式中a是人工湿地的横截面积；

将流量qi,j与监测得到的流量监测值q对比，如果|1-qi,j/q|＞0.05，则改变初始设定的渗透系数ki,j的取值，直至|1-qi,j/q|≤0.05；

步骤2-3-4，保存计算得到孔隙流速ui,j，bod浓度c’i,j，累计生物膜量σi,j，孔隙率ni,j和内部不同层的渗透系数ki,j，其中，i＝1,2,……m(m为最大划分层数)。

本发明利用一些简单易得的参数，如填料粒径，进水特征等，对各种不同的垂直流湿地不同运行情况下的堵塞时间进行了预测，为解决堵塞问题提供了技术支持。

有益效果：本发明方法实现了利用简单易得的参数快速预测生物堵塞发生的时间，可以定量的预测空隙中累积的生物膜质量。本发明为预测生物堵塞提供了有效方法，具有一定的实际运用价值。

附图说明

下面结合附图和具体实施方式对本发明做更进一步的具体说明，本发明的上述和/或其他方面的优点将会变得更加清楚。

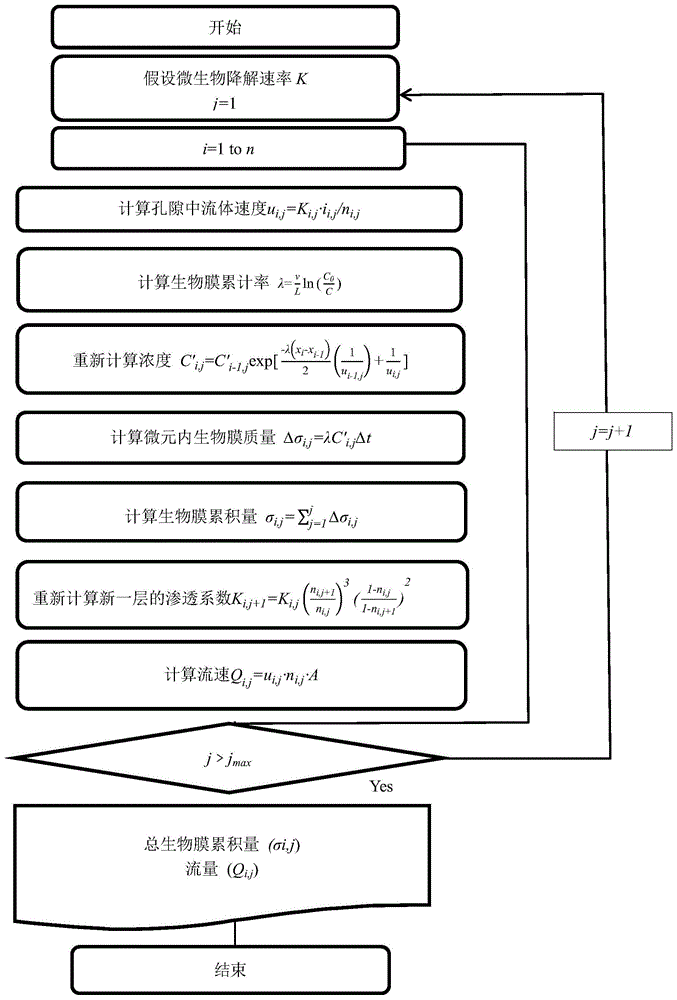
图1为计算流程图。

图2为孔隙率实测值与计算值对比图。

图3为渗透系数实测值与计算值对比图。

图4为bod浓度实测值与计算值对比图。

图5为计算累计生物膜量曲线图。

具体实施方式

本发明提供了一种人工湿地生物堵塞的预测计算方法，包括：在物质迁移和孔隙堵塞的过程中，孔隙率的变化往往是个动态的变化过程。基于此变化过程，在多孔介质中，结合生物膜累积的一维物质传输反应方程建立反应部分方程与生物膜生长速率方程。如方程(1)、(2)、(3)所示。

c是水中的bod浓度(g/cm³)，t是时间(d)，u是孔隙中的流体速度(cm/s)，x是距离(cm)。reaction为反应部分方程，如下所示。

反应部分方程：

k是微生物降解速率(day^-1)。biomass是生物膜的量，是一个随时间变化的量，所以生物膜的生长速率方程

kd是生物膜的死亡率(day^-1)。

在计算过程中有如下假设：

a.剪切力对生物膜的重要性和敏感性经常在文献中争论，到现在为止也没有独特的方法来鉴别。据前人研究，由于水流剪切力而脱落的生物膜可以被忽略。所以我们没有考虑水流剪切力的作用。

b.忽略植物根系对水流的影响。

c.不区别考虑微生物活的细胞和胞外聚合物(eps)。由于生物膜95％都是由水组成的，故近似的认为其密度接近于水。

采用逐步迭代计算法建立湿地生物堵塞过程计算模型。它能够估算生物膜的质量(σi,j)，流量(qi,j)和累积速率(vn)。每一步的计算过程如图1所示，其中下标i和j分别代表空间索引和时间索引。

其中，流量(qi,j)是随着时间监测的，目的是为了预测生物膜的累积速率。采用不断试错的方法估算初始微生物降解速率k，给定初始值k后，其余不同的参数，如孔隙流速(ui,j)，bod浓度(c,i,j)，生物膜累积量(σi,j)，孔隙率(ni,j)和内部不同层的渗透系数(ki,j)便可通过图1一步一步计算出来。

相较于进水悬浮物引起的物理堵塞，填料孔隙间发生化学反应产生胶体或沉淀引起的化学堵塞，人工湿地中的生物堵塞更具普遍性，其后果也更为严重。目前主要基于潜流湿地堵塞区的电阻率较未堵塞区低的特征对人工湿地生物堵塞进行监测。虽然该方法能一定程度上捕捉堵塞位置，但其操作复杂，且不能提前预测。因此参数简单的生物堵塞预测计算方法对保障人工湿地平稳高效运行有着重要意义。

实施例

用有机玻璃制作了6个高70厘米、直径30厘米的实验室规模的湿地柱，用于构建垂直流污水反应容器。柱状反应容器上部种植香蒲，其根茎延伸约10-15厘米深。柱子内填充有平均粒径为0.15毫米的细砂，填充至50厘米深。柱内底部覆盖着5厘米深的大卵石作为支撑层。废水从基质表面进入，通过柱底部插入的出口流出。为了计算水力传导率，每层的水头损失由设置在柱深为5、10、15、25、35和50厘米处的压力计测量。将硅胶孔放置在柱状反应容器壁上，与压力计对称排布，便于运用医用注射器对孔隙水进行取样，以测量ph值、电势，及溶解氧的含量。将6个柱子分为两组，分别配置葡萄糖溶液作为人工废水加入到柱状容器中，调节生化需氧量(bod)浓度为600毫克/升和300毫克/升。将k2hpo4、co2(nh2)2和(nh4)2so4作为氮源与磷源加入其中使总磷和总氮浓度分别约为2.0±0.5毫克/升和10.0±0.5毫克/升，以保持植物营养。分别用蠕动泵以1.0立方米/平方米/天的水力负荷连续操作。每组进行三次重复。

本实施例中要使用到的参数如表1所示：

表1

用排水法测定基质的孔隙率。水力传导率采用可变水头法测定。总磷、总氮和生化需氧量是根据标准方法测定的。基底中沉积着两种固体，一种是砾石间孔隙中的固体；另一种是附着在砾石表面的固体。在本实验结束后湿地柱被打破。将填料分成六层(即0-5厘米、5-10厘米、10-15厘米、15-25厘米、25-35厘米、35-50厘米)，并分别取出。将不同层的沙子放入一个大的超声波清洗机中，加入蒸馏水。然后将浸泡溶液通过预干燥的微孔膜(0.45微米)过滤。将滤膜置于105度温控干燥箱中，过滤前后的重量差为剥离生物膜的干重。通过以上步骤，可测得孔隙率，渗透系数，bod浓度等数值。下面运用本发明所建立的计算方法模型举例验证。

计算流程图中各公式推导过程：

在多孔介质中，考虑生物膜累积的一维物质传输反应方程用如方程(1)表示：

式中，c是水中的bod浓度(g/cm³)，t是时间(d)，u是孔隙中的流体速度(cm/s)，x是距离(cm)。reaction为反应部分方程。

反应部分用方程(2)表示：

式中，k是微生物降解速率(day^-1)。biomass是生物膜的量，它是一个随时间变量，所以生物膜的生长速率用如方程(3)表示：

式中，kd是生物膜的死亡率(day^-1)。

孔隙流速(ui,j)可用式(4)表示：

ui,j＝ki,j·ii,j/ni,j(4)

式中，ii,j是水力梯度，ki,j和ni,j分别为内部不同层的渗透系数和孔隙率。

尽管生物膜的浓度会随着流体的迁移会发生变化，但是在一个有限的小网格中，我们假设这个值是一个常数，即这个浓度在区间xi-1和xi之间可以用式(5)表示：

式中，xi与xi-1表示相邻两空间点同一时刻得坐标，ui,j为内部不同层的孔隙流速。c’i,j表示bod浓度。λ为生物膜累计系数。

累积的过程根据前人的过滤研究，本发明采用一级方程描述此过程，用式(6)表示：

式中，σi,j表示生物膜量。c’i,j表示bod浓度。λ为生物膜累计系数。

总的累积的生物膜可以用式(7)表示：

式中，c’i,j为内部不同层的bod浓度，λ为生物膜累计系数，δt为时间间隔。

累积的生物膜可以改变孔隙率。在位置i和时间步长为j+1的可以更新为式(8)：

当假设ni,j无限接近于ni,j+1时，这个方程可以简化为方程(9)：

式中，n0是初始孔隙率，ρs是生物膜的密度。基于随孔隙率改变的kozeny-carman的方程，内部不同层的渗透系数在时间步长为j+1时可以更新为空间索引为i的点，如式(10)所示：

式中，ki,j和ni,j分别为内部不同层的渗透系数和孔隙率，ki,j+1和ni,j+1分别为内部不同层时间步长为j+1的渗透系数和孔隙率。

由于生物膜在孔隙的累积会使孔隙流速降低，流量的计算过程如式(11)所示：

qi,j＝ui,j·ni,j·a(11)

式中，a是人工湿地单元柱的横截面积，ui,j和ni,j分别为内部不同层的孔隙流速和孔隙率。如果计算得到的流量和观察的流量有较大偏差，初始设定的k就进行调整直到两者的值足够靠近。

沉积系数λ(即生物膜累积系数)是图1中关键参数之一，可以根据如下公式(12)计算：

其中l是柱深(长度)，c是流出的bod浓度，c0是流入的bod浓度，ν是流速。

将如表1所示的计算参数带入流程图中，计算输出孔隙率变化、渗透系数、bod浓度，和累积的生物膜变化的值。

将观测数据与仿真数据进行可视化处理，如下列各图所示(图2至图5)：

(1)由图2可以看出，所有不同深度的人工湿地填料的孔隙率都是随着时间下降的。而0-5cm和5-10cm的孔隙率下降速率是最快的，下降的也是最多的，这和很多学者的研究结果一致，即堵塞基本发生在填料的表层。同时，对模拟值和实测值进行进一步对比，也可发现两者吻合趋势一致。

(2)由图3可以看出，所有不同深度的人工湿地填料的渗透系数都是随着时间下降的，这和孔隙率的规律一致。这里值得注意的是5-10cm的渗透系数在湿地运行前期(40天之前)的渗透系数是最高的，这可能5-10cm填料处是植物根系存在但并非最茂盛区，根系起到部分疏导水流的作用，使得此深度的渗透系数比其它深度的渗透系数高。同时，对模拟值和实测值进行进一步对比，除了5-10cm处渗透系数的模拟值和实测值相差较大，其余吻合较好，这是因为本发明建立的生物堵塞模型忽略了植物根系的作用。

(3)由图4可以看出，bod在不同深度都有一定程度的降解。按每cm的填料深度来计算，对bod去除率最大的是表层0-5cm(2％/cm厚度填料)，底部35-50cm是去除率最低的(1.2％/cm厚度填料)。对模拟值和实测值进行进一步对比，除了10-15cm处渗透系数的模拟值比实测值明显偏小之外，其余吻合较好，这是因为本发明建立的生物堵塞模型忽略植物根系的作用，而填料的10-15cm处是根系生长茂盛之处，大量微生物附着在根系表面，增加了对bod的去除率。

(4)按照流程图计算了累积在孔隙中的生物膜量随时间变化，如图5所示。从图中可以看出，累积的生物膜量随着深度逐渐减少，累积速率在不同时间段也不相同。结合对孔隙率变化趋势、渗透系数变化趋势和bod降解变化趋势的分析，生物膜累积的计算值是基本合理的，可为堵塞的预测提供有利的依据。

以上分析表明，计算结果合理。根据人工湿地生物堵塞机理，本发明结合实验实例进行了数值模拟，比对如上所示。根据模拟结果的对比，说明人工湿地生物堵塞预测计算模型的计算结果很接近实际生物堵塞的特性，当符合假设条件时尤为适用。说明推导出的人工湿地生物堵塞预测数学模型是适用的，这为解决人工湿地生物堵塞何时进行修复如何进行修复提供技术支持。具体来说，可以根据计算得出的堵塞时间进行调整进水污染负荷或者调整填料粒径大小来合理设计并利用人工湿地进行污水处理；或者根据堵塞预测时间进行定期轮休，延长人工湿地使用年限。

本发明提供了一种人工湿地生物堵塞的计算方法，具体实现该技术方案的方法和途径很多，以上所述仅是本发明的优选实施方式，应当指出，对于本技术领域的普通技术人员来说，在不脱离本发明原理的前提下，还可以做出若干改进和润饰，这些改进和润饰也应视为本发明的保护范围。本实施例中未明确的各组成部分均可用现有技术加以实现。