崩塌落石地质灾害中钢筋混凝土桩板墙的动态工程响应测算方法

1.本发明涉及地质工程技术领域，尤其是一种崩塌落石地质灾害中钢筋混凝土桩板墙的动态工程响应测算方法。


背景技术：

2.近年来，我国西部乃至世界范围内的山区地质灾害频发，其中崩塌落石灾害在所有地质灾害中的占比高达17％，已成为继滑坡之后的第二大斜坡地质灾害。其具有发生突然、可预见性差、速度快、能量高、破坏范围广、运动路线复杂及监测预警困难等特点，因而对公路、铁路等基础设施造成了严重威胁，引起了人们的高度重视。针对近年来出现的一些强震诱发的高位危岩崩塌落石现象，不少学者提出了一种新型的被动拦石方案——桩板拦石墙，即在抗滑桩板结构基础上增加缓冲层而成的复式结构，其具有占地小、拦截性能好、易于施工等优点，对于防护高冲击能量的落石具有突出优点，在实际应用中取得了初步的良好效果。
3.然而由于该拦石结构出现时间相对较短，因此目前对其开展的研究也相对较少，但是对其他类似的墙体防护结构则有一些相关研究，为此这里就对类似的相关研究现状进行回顾，以期对本研究有所启发。概括而言，目前的研究主要集中在试验研究、理论研究和数值模拟等3个方面。首先在试验研究方面，hearn等首次开展了加筋防护挡墙的落石冲击试验，结果表明加筋防护挡墙可以有效拦截落石，但是由于试验时落石的冲击动能达到1410kj，因此挡墙正面出现了约0.3～0.8m的凸出变形。peila等也开展了大比例加筋土拦石墙结构模型的抗冲击性能现场试验研究，所采用的落石为重达9000kg的混凝土块，以30m/s的速度冲击墙体，试验结果表明虽然落石冲击会造成墙体产生一定的变形，但其仍是一种有效的落石冲击防护结构。arnold等首先基于位移模型提出了悬臂式钢筋混凝土挡墙在落石冲击下的挠度解析解模型，而后采用大尺度的卵石冲击模型试验对钢筋混凝土挡墙的动态响应进行了测试，从而验证了模型的合理性。其次，在理论研究方面，目前落石对钢筋混凝土结构的冲击力计算主要是基于hertz接触理论，但是该理论是以弹性力学为基础，而在落石冲击下钢筋混凝土结构通常会出现塑性特性，为此何思明等视构筑物为理想弹塑性体，对hertz接触理论进行了弹塑性修正，进而提出了考虑材料弹塑性变形的泥石流大块石冲击力计算公式。陈颖骐等基于hertz弹性碰撞理论和thornton弹塑性假设，通过考虑构造物材料特性、冲击物相对尺寸、结构变位等因素，建立了落石对构造物的冲击力修正方程，并将其应用于锚索抗滑桩的冲击计算。由于落石对钢筋混凝土结构的冲击不仅与落石特性有关，而且还与钢筋混凝土结构的力学性质有关，因此不少学者综合考虑hertz接触理论与钢筋混凝土结构的力学性质，提出了落石冲击下钢筋混凝土结构动力响应计算方法，如olsson基于hertz接触理论和各向异性复合板的冲击压痕理论建立了小质量冲击下各向异性复合板动态响应计算模型。考虑冲击作用下层状复合板的塑性变形及损伤效应，zheng等基于hertz接触理论和冲击作用下板的永久压痕理论建立了相应的冲击力计算公式。王
东坡等在此基础上，研究了落石冲击下钢筋混凝土板的弹塑性动力响应。最后，在数值模拟方面，胡卸文等采用abaqus软件模拟了落石冲击下桩板拦石墙的动力响应，模拟得到了落石冲击过程中动力学全过程，即首先是弹性压入阶段、而后是塑性压入阶段，最后是压入达到最大值后的卸荷回弹阶段，这与弹塑性理论分析结果完全吻合。yan等采用ansys/ls
‑
dyna软件模拟研究了椭圆形落石冲击下钢筋混凝土板的动态响应，认为落石形状和冲击角度将影响到对钢筋混凝土板的冲击力及其动态响应。邓力源等采用ansys/ls
‑
dyna软件模拟研究了落石冲击下废旧轮胎的耗能性能，认为废旧轮胎吸能作用明显，可以有效减缓落石对刚性拦石墙的冲击作用，进而提高其防护能力。
4.然而虽然很多学者都对该问题进行了深入研究，但是仍存在以下两方面的主要问题：(1)由于落石冲击下钢筋混凝土桩板墙的动态响应是一个明显的动力学过程，钢筋混凝土桩板墙的动态响应可以分为3个阶段：碰撞初期的弹性压缩阶段、墙体应力达到其极限屈服强度后的塑性变形阶段以及墙体达到其最大压缩变形后的弹性回弹阶段。尽管zheng、王东坡等的研究也是根据上述3个阶段进行的，但是在第二阶段即塑性变形阶段，他们均认为钢筋混凝土桩板墙的弹性模量是不变的，这显然是不符合实际情况的。因为在塑性变形阶段，钢筋混凝土桩板墙的弹性模量随着塑性变形的增加是不断降低的，这是因为材料的塑性变形过程，即为损伤过程，因此材料的弹性常数必然会随着塑性变形的增加而逐渐降低。(2)前人的研究多给出了钢筋混凝土桩板墙受到的冲击力随时间的变化曲线
[5，10
‑
13]
，而并未给出冲击力随墙体变形的关系曲线，因而无法获得落石冲击下墙体的永久变形，这将不利于后期对桩板墙安全性的评估。


技术实现要素：

[0005]
本发明要解决的技术问题是提供一种崩塌落石地质灾害中钢筋混凝土桩板墙的动态工程响应测算方法。
[0006]
为解决上述技术问题，本发明所采取的技术方案如下。
[0007]
在崩塌落石地质灾害中获取兼顾材料损伤的接触压力、最大接触压应力与接触变形的方法，该方法包括如下步骤：
[0008]
设定接触面为半径为a的圆，首先对接触压应力分布进行确认：
[0009][0010]
式中：p(r)为接触压应力，p为接触压力，a为接触半径；最大接触压应力p
max
位于r＝0处：
[0011][0012]
接触变形由两部分组成：
[0013]
δ＝δ1+δ2ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(3)
[0014]
式中：δ1、δ2分别为2个接触体的变形量；
[0015]
接触变形量与接触面积之间有如下关系：
[0016]
a2＝rδ
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(4)
[0017]
式中：r为等效半径，r1、r2为2个球体的半径；
[0018]
接触压力p、最大接触压应力p
max
与接触变形δ之间的关系为：
[0019][0020]
式中：e为等效弹性模量，e1、μ1、e2、μ2为两个接触体的弹性模量和泊松比；
[0021]
进一步的，根据球形颗粒在冲击荷载下的荷载
‑
变形响应特性构建相应的冲击损伤理论模型：
[0022][0023]
式中：d为球形颗粒直径，为有效刚度，
[0024]
式中：d为球形颗粒的冲击损伤，k为初始刚度；
[0025]
将冲击损伤变量d定义为：
[0026][0027]
式中：δ
c
为球形颗粒发生冲击破坏时的压缩变形量，当δ＝δ
c
，损伤d＝1；γ为冲击损伤指数；
[0028]
进一步的，将颗粒的损伤变量d定义为：
[0029][0030]
其中：e分别为颗粒的有效弹性模量和初始弹性模量；δ
y
、δ
m
、δ
c
分别为颗粒发生初始屈服时所对应的接触变形量、颗粒碰撞过程中的最大接触变形量及颗粒发生完全破坏即d＝1时对应的变形量，三者之间满足δ
y
<δ
m
≦δ
c
；由此可得到考虑材料损伤的接触压力、最大接触压应力与接触变形之间的关系为：
[0031][0032]
在崩塌落石地质灾害中获取落石对钢筋混凝土桩板墙冲击力的方法，该方法包括如下步骤：
[0033]
落石确认为以速度v0运动的质点，钢筋混凝土桩板墙为静止的平面，将冲击速度沿水平和垂直方向分解：
[0034]
v
x
＝v
0 sinθ，v
y
＝v0cosθ
ꢀꢀꢀꢀꢀꢀꢀ
(11)
[0035]
式中：v0、v
x
、v
y
分别为落石接触到钢筋混凝土桩板墙瞬时的总冲击速度、水平冲击速度和垂直冲击速度；θ为冲击角度；
[0036]
对钢筋混凝土桩板墙造成冲击破坏的是水平冲击，仅考虑落石的水平冲击作用，有：
[0037][0038]
式中：m1、m2分别为钢筋混凝土桩板墙和落石的质量；v1为钢筋混凝土桩板墙的运动速度；p为落石对钢筋混凝土桩板墙的冲击力；可得：
[0039][0040][0041]
式中：m为等效质量，
[0042]
对δ积分：
[0043][0044]
在最大压缩量时，得到最大压缩量为：
[0045][0046]
进一步求出落石产生的最大冲击力：
[0047][0048]
进一步得到相应的最大落石冲击压应力为：
[0049][0050]
考虑由于冲击碰撞导致的材料损伤，得到考虑损伤的落石最大冲击力为：
[0051][0052]
崩塌落石地质灾害中钢筋混凝土桩板墙动态响应的获取方法，将钢筋混凝土桩板墙在落石冲击下的冲击力
‑
变形关系曲线划分3个阶段：
[0053]
①
阶段ⅰ：碰撞初期的弹性加载阶段，落石与钢筋混凝土桩板墙二者之间的接触力
确认为弹性接触，得到：
[0054][0055]
式中：δ
y
为钢筋混凝土桩板墙产生初始屈服时的变形值；
[0056]
②
阶段ⅱ：混凝土桩板墙的塑性损伤加载阶段，接触冲击力超过墙体的屈服强度时导致其产生塑性变形出现损伤，考虑损伤，得到：
[0057][0058]
式中：δ
m
为钢筋混凝土桩板墙的最大变形值；
[0059]
③
阶段ⅲ：卸载阶段，当钢筋混凝土桩板墙达到压缩最大变形时，落石冲击速度减小为0，墙体积累的弹性变形能发生回弹释放；确认接触冲击力与变形的关系为：
[0060][0061]
式中：d
m
为与钢筋混凝土桩板墙卸载前最大变形值δ
m
所对应的损伤。
[0062]
作为本发明的一种优选技术方案，在第
③
阶段，当卸荷完成后，接触应力p(δ)为零，获取对应的墙体残余变形量δ0，即为落石冲击对钢筋混凝土桩板墙造成的塑性变形。
[0063]
作为本发明的一种优选技术方案，待定常数δy的确定方法为：
[0064]
钢筋混凝土桩板墙初始屈服时的变形值δ
y
所对应的应力为其初始屈服强度σ
py
，通过材料力学试验测得；落石对钢筋混凝土桩板墙的接触力p
y
与其屈服强度σ
py
之间满足：
[0065][0066]
式中：e、μ分别为材料的弹性模量和泊松比；a
y
是与泊松比μ有关的材料常数，当μ＝0.3和0.4时，a
y
＝1.61和1.74；材料的初始屈服点为弹性段和塑性损伤段的交界点，其同时属于弹性段和塑性损伤段，已知材料的屈服强度σ
py
，即可得到此时对应的变形量δ
y
。
[0067]
作为本发明的一种优选技术方案，待定常数δ
m
的确定方法为：
[0068]
钢筋混凝土桩板墙的最大冲击力和最大冲击变形同时出现，可得：
[0069][0070]
得到一个关于δ
m
的方程，其中δ
c
为材料发生完全破坏时的冲击变形量，通过试验测得；通过迭代求解该方程即可得到δ
m
。
[0071]
作为本发明的一种优选技术方案，该方法包括如下步骤：
[0072]
a、获取考虑材料损伤的接触压力、最大接触压应力与接触变形：
[0073]
接触面为半径为a的圆，接触压应力分布为：
[0074]
[0075]
式中：p(r)为接触压应力，p为接触压力，a为接触半径；最大接触压应力p
max
位于r＝0处：
[0076][0077]
接触变形由两部分组成：
[0078]
δ＝δ1+δ2ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(3)
[0079]
式中：δ1、δ2分别为2个接触体的变形量；
[0080]
接触变形量与接触面积之间有如下关系：
[0081]
a2＝rδ
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(4)
[0082]
式中：r为等效半径，r1、r2为2个球体的半径；
[0083]
接触压力p、最大接触压应力p
max
与接触变形δ之间的关系为：
[0084][0085]
式中：e为等效弹性模量，e1、μ1、e2、μ2为两个接触体的弹性模量和泊松比；
[0086]
进一步的，根据球形颗粒在冲击荷载下的荷载
‑
变形响应特性构建相应的冲击损伤理论模型：
[0087][0088]
式中：d为球形颗粒直径，为有效刚度，
[0089]
式中：d为球形颗粒的冲击损伤，k为初始刚度；
[0090]
将冲击损伤变量d定义为：
[0091][0092]
式中：δ
c
为球形颗粒发生冲击破坏时的压缩变形量，当δ＝δ
c
，损伤d＝1；γ为冲击损伤指数；
[0093]
进一步的，将颗粒的损伤变量d定义为：
[0094][0095]
其中：e分别为颗粒的有效弹性模量和初始弹性模量；δ
y
、δ
m
、δ
c
分别为颗粒发生初始屈服时所对应的接触变形量、颗粒碰撞过程中的最大接触变形量及颗粒发生完全破坏即d＝1时对应的变形量，三者之间满足δ
y
<δ
m
≦δ
c
；由此可得到考虑材料损伤的接触压力、最
大接触压应力与接触变形之间的关系为：
[0096][0097]
b、获取落石对钢筋混凝土桩板墙的冲击力：
[0098]
落石确认为以速度v0运动的质点，而钢筋混凝土桩板墙为静止的平面，将冲击速度沿水平和垂直方向分解：
[0099]
v
x
＝v0sinθ，v
y
＝v0cosθ
ꢀꢀꢀꢀꢀꢀꢀ
(11)
[0100]
式中：v0、v
x
、v
y
分别为落石接触到钢筋混凝土桩板墙瞬时的总冲击速度、水平冲击速度和垂直冲击速度；θ为冲击角度；
[0101]
对钢筋混凝土桩板墙造成冲击破坏的是水平冲击，仅考虑落石的水平冲击作用，有：
[0102][0103]
式中：m1、m2分别为钢筋混凝土桩板墙和落石的质量；v1为钢筋混凝土桩板墙的运动速度；p为落石对钢筋混凝土桩板墙的冲击力；可得：
[0104][0105][0106]
式中：m为等效质量，
[0107]
对δ积分：
[0108][0109]
在最大压缩量时，得到最大压缩量为：
[0110][0111]
进一步求出落石产生的最大冲击力：
[0112][0113]
进一步得到相应的最大落石冲击压应力为：
[0114]
[0115]
考虑由于冲击碰撞导致的材料损伤，得到考虑损伤的落石最大冲击力为：
[0116][0117]
c、确认钢筋混凝土桩板墙的动态响应：
[0118]
将钢筋混凝土桩板墙在落石冲击下的冲击力
‑
变形关系曲线划分3个阶段：
[0119]
①
阶段ⅰ：碰撞初期的弹性加载阶段，落石与钢筋混凝土桩板墙二者之间的接触力确认为弹性接触，得到：
[0120][0121]
式中：δ
y
为钢筋混凝土桩板墙产生初始屈服时的变形值；
[0122]
②
阶段ⅱ：混凝土桩板墙的塑性损伤加载阶段，接触冲击力超过墙体的屈服强度时导致其产生塑性变形出现损伤，考虑损伤，得到：
[0123][0124]
式中：δ
m
为钢筋混凝土桩板墙的最大变形值；
[0125]
③
阶段ⅲ：卸载阶段，当钢筋混凝土桩板墙达到压缩最大变形时，落石冲击速度减小为0，墙体积累的弹性变形能发生回弹释放；确认接触冲击力与变形的关系为：
[0126][0127]
式中：d
m
为与钢筋混凝土桩板墙卸载前最大变形值δ
m
所对应的损伤；
[0128]
在第
③
阶段，当卸荷完成后，接触应力p(δ)为零，获取对应的墙体残余变形量δ0，即为落石冲击对钢筋混凝土桩板墙造成的塑性变形；
[0129]
待定常数δ
y
的确定方法为：
[0130]
钢筋混凝土桩板墙初始屈服时的变形值δ
y
所对应的应力为其初始屈服强度σ
py
，通过材料力学试验测得；落石对钢筋混凝土桩板墙的接触力p
y
与其屈服强度σ
py
之间满足：
[0131][0132]
式中：e、μ分别为材料的弹性模量和泊松比；a
y
是与泊松比μ有关的材料常数，当μ＝0.3和0.4时，a
y
＝1.61和1.74；材料的初始屈服点为弹性段和塑性损伤段的交界点，其同时属于弹性段和塑性损伤段，已知材料的屈服强度σ
py
，即可得到此时对应的变形量δ
y
；
[0133]
待定常数δ
m
的确定方法为：钢筋混凝土桩板墙的最大冲击力和最大冲击变形同时出现，可得：得到一个关于δm的方程，其中δc为材料发生完全破坏时的冲击变形量，通过试验测得；通过迭代求解该方程即可得到δ
m
。
[0134]
采用上述技术方案所产生的有益效果在于：本发明针对现有技术在多个方面的不足和问题，在经典接触理论的基础上，考虑落石冲击对钢筋混凝土桩板墙造成的损伤，提出考虑损伤接触理论并用于地质灾害工程实践；同时，根据落石冲击下钢筋混凝土桩板墙的动态响应过程，提出落石冲击下钢筋混凝土桩板墙的动态损伤模型，并对模型参数确定方法进行了延伸；最后，本发明进行了面向地质实践实例研究，显示落石冲击速度与半径对钢筋混凝土桩板墙的动态力学响应影响较大，而钢筋混凝土桩板墙的损伤参数δ
c
和γ对计算结果影响较小，但是当γ较小时，其影响较为显著；显示本发明能够很好地描述钢筋混凝土桩板墙在落石冲击下的动态力学行为，能够为工程设计提供高价值参考，具有十分良好的应用前景。
附图说明
[0135]
图1为力学界面接触示意图。
[0136]
图2为落石冲击钢筋混凝土桩板墙计算模型。
[0137]
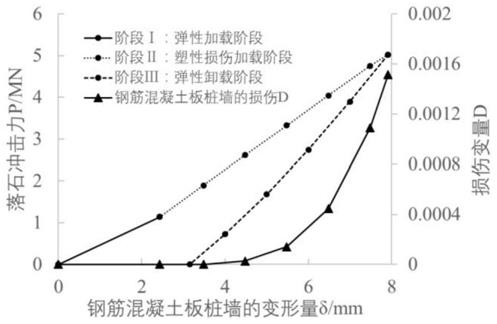
图3为落石冲击下钢筋混凝土板桩墙的冲击力
‑
变形关系曲线。
[0138]
图4为不同落石速度下钢筋混凝土板桩墙的冲击力
‑
变形曲线。
[0139]
图5为不同落石半径下钢筋混凝土板桩墙的冲击力
‑
变形曲线。
[0140]
图6为不同损伤参数下钢筋混凝土板桩墙的冲击力
‑
变形曲线。
具体实施方式
[0141]
以下实施例详细说明了本发明。本发明所使用的各种原料及各项设备均为常规市售产品，均能够通过市场购买直接获得。
[0142]
在以下实施例的描述中，为了说明而不是为了限定，提出了诸如特定系统结构、技术之类的具体细节，以便透彻理解本申请实施例。然而，本领域的技术人员应当清楚，在没有这些具体细节的其它实施例中也可以实现本申请。在其它情况中，省略对众所周知的系统、装置、电路以及方法的详细说明，以免不必要的细节妨碍本申请的描述。
[0143]
应当理解，当在本申请说明书和所附权利要求书中使用时，术语“包括”指示所描述特征、整体、步骤、操作、元素和/或组件的存在，但并不排除一个或多个其它特征、整体、步骤、操作、元素、组件和/或其集合的存在或添加。
[0144]
还应当理解，在本申请说明书和所附权利要求书中使用的术语“和/或”是指相关联列出的项中的一个或多个的任何组合以及所有可能组合，并且包括这些组合。
[0145]
如在本申请说明书和所附权利要求书中所使用的那样，术语“如果”可以依据上下文被解释为“当...时”或“一旦”或“响应于确定”或“响应于检测到”。类似地，短语“如果确定”或“如果检测到[所描述条件或事件]”可以依据上下文被解释为意指“一旦确定”或“响应于确定”或“一旦检测到[所描述条件或事件]”或“响应于检测到[所描述条件或事件]”。
[0146]
另外，在本申请说明书和所附权利要求书的描述中，术语“第一”、“第二”、“第三”等仅用于区分描述，而不能理解为指示或暗示相对重要性。
[0147]
在本申请说明书中描述的参考“一个实施例”或“一些实施例”等意味着在本申请的一个或多个实施例中包括结合该实施例描述的特定特征、结构或特点。由此，在本说明书中的不同之处出现的语句“在一个实施例中”、“在一些实施例中”、“在其他一些实施例中”、
“
在另外一些实施例中”等不是必然都参考相同的实施例，而是意味着“一个或多个但不是所有的实施例”，除非是以其他方式另外特别强调。术语“包括”、“包含”、“具有”及它们的变形都意味着“包括但不限于”，除非是以其他方式另外特别强调。
[0148]
实施例1、弹性接触理论及其改进
[0149]
参见图1，假设接触面为半径为a的圆，由此hertz给出了2个球体在接触压力p下弹性接触的完备解：
[0150]
接触压应力分布为：
[0151][0152]
式中：p(r)为接触压应力，p为接触压力，a为接触半径。最大接触压应力p
max
位于r＝0处：
[0153][0154]
接触变形由两部分组成：
[0155]
δ＝δ1+δ2ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(3)
[0156]
式中：δ1、δ2分别为2个接触体的变形量。
[0157]
接触变形量与接触面积之间有如下关系：
[0158]
a2＝rδ
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(4)
[0159]
式中：r为等效半径，r1、r2为2个球体的半径。
[0160]
接触压力p、最大接触压应力p
max
与接触变形δ之间的关系为：
[0161][0162]
式中：e为等效弹性模量，e1、μ1、e2、μ2为两个接触体的弹性模量和泊松比。
[0163]
上述hertz接触理论仅适用于材料处于弹性变形阶段，而在实际工程中由其计算出的接触力往往偏大，这是因为当接触压应力达到材料屈服强度时，材料将产生塑性变形，此时经典的hertz接触理论将不再适用。为此不少学者对其进行了改进，目前主要有两类改进模型：hertz塑性接触理论和损伤接触理论。前者认为当接触应力达到材料的屈服强度时，材料将发生塑性变形，如何思明、thornton等提出了基于理想弹塑性模型的hertz塑性接触理论，由此计算得到的冲击力明显小于相应的经典hertz接触理论计算得到的冲击力，也更加符合实际情况。然而随着损伤力学的发展，不少学者也开始将其引入hertz接触理论，如travares等以hertz接触理论和连续介质损伤理论为基础，根据球形颗粒在冲击荷载下的荷载
‑
变形响应特性构建了相应的冲击损伤理论模型：
[0164]
[0165]
式中：d为球形颗粒直径，为有效刚度，
[0166]
式中：d为球形颗粒的冲击损伤，k为初始刚度。
[0167]
并将冲击损伤变量d定义为：
[0168][0169]
式中：δ
c
为球形颗粒发生冲击破坏时的压缩变形量，当δ＝δ
c
，损伤d＝1；γ为冲击损伤指数。
[0170]
那么由式(8)可知，球形颗粒的任何冲击接触变形都会导致损伤，然而根据hertz接触理论和室内压痕试验可知：当球形颗粒接触变形量δ小于初始屈服变形量δ
y
时，颗粒物质处于完全弹性接触状态，没有损伤产生，此时d＝0。显然式(8)无法描述颗粒处于完全弹性接触状态时的情形，这是该模型的缺陷。
[0171]
由于自然界中的岩石和混凝土都是天然的损伤材料，其本身存在着大量的微裂纹、微孔洞等细观缺陷，因此，颗粒之间的碰撞将不可避免地会导致微裂纹的萌生、扩展及汇聚，进而导致颗粒宏观物理力学性质的劣化，具体表现为颗粒弹性模量的降低，直至最后发生破坏。因此可以用弹性模量的降低来定义损伤变量。典型的颗粒碰撞荷载
‑
接触变形曲线可分为4个阶段：颗粒的初始碰撞阶段、弹性碰撞阶段、塑性损伤碰撞阶段和卸荷回弹阶段，由于第一阶段较短，通常忽略。在弹性接触阶段，颗粒之间的荷载
‑
接触变形符合hertz弹性接触理论，颗粒接触变形属于弹性变形，因此不会有损伤产生；而当接触压力超过颗粒的初始屈服压力后，压力
‑
接触变形曲线开始偏离hertz弹性接触理论曲线，颗粒材料开始出现损伤，即进入塑性损伤碰撞阶段；当达到碰撞压力峰值即最大压缩变形量之后，就开始进入弹性卸荷回弹阶段，在此阶段变形为弹性，损伤保持不变。那么由此可将颗粒的损伤变量d定义为：
[0172][0173]
其中：e分别为颗粒的有效弹性模量和初始弹性模量；δ
y
、δ
m
、δ
c
分别为颗粒发生初始屈服时所对应的接触变形量、颗粒碰撞过程中的最大接触变形量及颗粒发生完全破坏即d＝1时对应的变形量，三者之间应满足δ
y
<δ
m
≦δ
c
。
[0174]
由此可得到考虑材料损伤的接触压力、最大接触压应力与接触变形之间的关系为：
[0175][0176]
实施例2、落石对钢筋混凝土桩板墙的冲击力
[0177]
假设落石为以速度v0运动的质点，而钢筋混凝土桩板墙为静止的平面，建立如图2所示计算模型。
[0178]
首先可将冲击速度沿水平和垂直方向分解：
[0179]
v
x
＝v0sinθ，v
y
＝v0cosθ
ꢀꢀꢀꢀꢀꢀꢀ
(11)
[0180]
式中：v0、v
x
、v
y
分别为落石接触到钢筋混凝土桩板墙瞬时的总冲击速度、水平冲击速度和垂直冲击速度；θ为冲击角度。
[0181]
由于对钢筋混凝土桩板墙造成冲击破坏的主要是水平冲击，因此这里仅考虑落石的水平冲击作用。根据牛顿第二定律，则有：
[0182][0183]
式中：m1、m2分别为钢筋混凝土桩板墙和落石的质量；v1为钢筋混凝土桩板墙的运动速度；p为落石对钢筋混凝土桩板墙的冲击力。
[0184]
那么由式(12)可得：
[0185][0186]
那么由式(5)和(13)可得：
[0187][0188]
式中：m为等效质量，
[0189]
对δ积分，可得：
[0190][0191]
在最大压缩量时，由此可得最大压缩量为：
[0192][0193]
把式(16)代入式(5)即可求出落石产生的最大冲击力：
[0194][0195]
那么由式(2)、(5)、(16)和(17)可得相应的最大落石冲击压应力为：
[0196][0197]
由第2节可知，当考虑由于冲击碰撞导致的材料损伤时，将式(9)代入式(17)，即可得到考虑损伤的落石最大冲击力为：
[0198]
[0199]
实施例3、钢筋混凝土桩板墙的动态响应
[0200]
工程实践表明，落石冲击力将会对钢筋混凝土桩板墙造成一定的损伤破坏，为此，采用考虑损伤的hertz接触理论将更符合实际情况。
[0201]
钢筋混凝土桩板墙在落石冲击下的冲击力
‑
变形关系曲线可分为3个阶段：
[0202]
①
阶段ⅰ：碰撞初期的弹性加载阶段
[0203]
在碰撞初期，由于落石对钢筋混凝土桩板墙的冲击力较小，相应地墙体的变形也较小，因此墙体仍处于弹性变形状态，二者之间的接触力满足弹性hertz接触理论，即：
[0204][0205]
式中：δ
y
为钢筋混凝土桩板墙产生初始屈服时的变形值。
[0206]
②
阶段ⅱ：混凝土桩板墙的塑性损伤加载阶段，即随着冲击过程的继续，接触冲击力及墙体变形均不断增加，当接触冲击力超过墙体的屈服强度时，将会导致其产生塑性变形，出现损伤，此时接触冲击力应满足考虑损伤的hertz接触理论，即：
[0207][0208]
式中：δ
m
为钢筋混凝土桩板墙的最大变形值。
[0209]
③
阶段ⅲ：卸载阶段，即当钢筋混凝土桩板墙达到压缩最大变形时，落石冲击速度减小为0，墙体积累的弹性变形能将发生回弹释放。在此阶段，墙体不会产生新的损伤，而已有的损伤也不会恢复，因此此阶段的墙体的弹性模量为其产生峰值变形时的弹性模量，其接触冲击力与变形的关系为：
[0210]
式中：d
m
为与钢筋混凝土桩板墙卸载前最大变形值δ
m
所对应的损伤。
[0211]
当卸荷完成后，接触应力p(δ)应为零，此时可求出对应的墙体残余变形量δ0，即为落石冲击对钢筋混凝土桩板墙造成的塑性变形。
[0212]
由式(20)～(22)可知，当进行钢筋混凝土桩板墙在落石冲击下的动力响应分析时，必须确定其中的待定常数δ
y
和δ
m
，下面讨论其确定方法。
[0213]
(1)δ
y
确定方法
[0214]
钢筋混凝土桩板墙初始屈服时的变形值δ
y
所对应的应力为其初始屈服强度σ
py
，这可以通过材料力学试验测得。vu
‑
quoc等以hertz接触理论为基础，认为当材料满足von mises屈服准则时，落石对钢筋混凝土桩板墙的接触力p
y
与其屈服强度σ
py
之间满足：
[0215][0216]
式中：e、μ分别为材料的弹性模量和泊松比；a
y
是与泊松比μ有关的材料常数，当μ＝0.3和0.4时，a
y
＝1.61和1.74。
[0217]
由于材料的初始屈服点为弹性段和塑性损伤段的交界点，因此其同时属于弹性段
和塑性损伤段，所以其应同时满足式(5)中的第二式和式(23)，若已知材料的屈服强度σ
py
，即可求出此时对应的变形量δ
y
。
[0218]
(2)δ
m
确定方法
[0219]
由前述可知，钢筋混凝土桩板墙的最大冲击力和最大冲击变形是同时出现的，因此由式(19)和(21)可得：
[0220][0221]
由此可得一个关于δ
m
的方程(其中δ
c
为材料发生完全破坏时的冲击变形量，可以通过试验测得)，通过迭代求解该方程即可得到δ
m
。
[0222]
实施例4、实例研究
[0223]
计算模型如图2所示，假设落石接触到钢筋混凝土桩板墙瞬间时的冲击速度为v0、冲击角度为θ，取落石计算参数为：形状为球形，半径为1.0m、密度2500kg/m3、质量10467kg、弹性模量20gpa、泊松比0.2、v0＝5m/s、θ＝30
°
；取两相邻桩体间的钢筋混凝土桩板墙为一个独立的研究对象，其计算参数为：形状为长方体，尺寸为3.0m
×
3.0m
×
0.3m、弹性模量10gpa、泊松比0.3、密度2600kg/m3、屈服强度σ
py
＝150mpa、损伤系数δ
c
＝30mm、γ＝4。
[0224]
计算流程及结果如下：
[0225]
①
阶段ⅰ：碰撞初期的弹性加载阶段
[0226]
首先由式(5)及(23)和上述计算参数，可得δ
y
＝2.43mm，对应的最大弹性冲击力为1.15mn，即钢筋混凝土桩板墙在落石冲击下的变形由0增加到2.43mm时，对应的接触冲击力相应地由0线性增加到1.15mn。
[0227]
②
阶段ⅱ：碰撞中期的塑性损伤加载阶段
[0228]
首先根据式(19)、(21)和(24)求得钢筋混凝土桩板墙的冲击变形最大值δ
m
＝7.91mm。那么在δ
y
～δ
m
之间取若干δ的值，然后代入式(21)即可求得接触冲击力p(δ)，然后利用这些点即可绘制得到混凝土桩板墙的塑性损伤加载曲线。
[0229]
③
阶段ⅲ：碰撞后期的弹性卸载阶段
[0230]
首先，由钢筋混凝土桩板墙的冲击变形最大值δ
m
＝7.91mm，可求得对应的最大损伤值d
m
＝0.00156。代入式(22)，另设接触冲击力p(δ)＝0，可求得对应的永久变形量δ0＝3.15mm。在δ
m
～δ0之间取若干值，利用式(22)可求得相应的接触冲击力p(δ)，然后利用这些点即可绘制得到钢筋混凝土桩板墙的弹性卸载曲线。
[0231]
由此可得到落石与钢筋混凝土桩板墙的冲击力、损伤与变形的关系曲线如图3所示，可以发现：
①
冲击力
‑
变形曲线可分为3段：弹性加载阶段、塑性损伤加载阶段和弹性卸载阶段。在弹性加载阶段，钢筋混凝土桩板墙发生弹性变形，落石对钢筋混凝土桩板墙的冲击力与钢筋混凝土桩板墙的变形满足线性关系；当冲击力增加到钢筋混凝土桩板墙的屈服强度时，钢筋混凝土桩板墙开始进入塑性损伤变形阶段。从曲线斜率上来看，塑性损伤加载阶段的斜率大于弹性加载阶段，这是由于钢筋混凝土在进入塑性后，会出现一个塑性强化阶段，即若使其产生较小的位移，就必须施加较大的力，因而导致塑性段曲线斜率变陡，这与何思明等得到的规律是一致的。在达到峰值冲击力之后，落石冲击速度减小为零，而后钢筋混凝土桩板墙开始发生卸荷回弹，钢筋混凝土桩板墙的弹性变形部分开始恢复，落石冲击力与总的变形量均逐渐减小。当落石冲击力减小为零时，对应的变形量即为钢筋混凝土
桩板墙的永久变形量即残余的塑性变形量。
②
由损伤
‑
变形曲线可以看出，在该算例中仅在阶段ⅱ有损伤产生，且最大损伤值仅为0.0015，即损伤较小，因此可以看出阶段ⅱ的曲线也近似线性关系。另外需要说明的是由式(9)所示的损伤变量定义看出，损伤值的大小与δ
c
和γ密切相关，因此钢筋混凝土桩板墙损伤演化规律的精确描述在很大程度上依赖于这两个损伤常数的准确测定，见图3。
[0232]
实施例5、参数敏感性分析
[0233]
由本文提出的计算模型可知，落石冲击下钢筋混凝土桩板墙的动态响应不仅与其本身的物理力学性质有关，而且还在很大程度上受落石参数的影响。为此，下面采用参数敏感性分析研究落石及钢筋混凝土计算参数对结果的影响。
[0234]
(1)落石速度
[0235]
这里取落石速度分别为2.5、5、7.5和10m/s，其余参数均不变，由如图4所示的计算结果可以看出：
①
随着落石冲击速度的增加，钢筋混凝土桩板墙产生的最大冲击变形则由3.17mm逐渐增加到4.66、6.24和7.91mm，相应地最大冲击力也由1.67mn逐渐增加到2.73、3.84和5.03mn，这说明落石冲击速度越大，其对钢筋混凝土桩板墙造成的冲击力就越大，相应地产生的最大冲击变形也就越大；
②
随着落石冲击速度的增加，钢筋混凝土桩板墙的残余变形则由0.25mm逐渐增加到1.0、2.0和3.15mm，即残余变形也越来越大，这说明落石冲击速度越大，钢筋混凝土桩板墙的塑性变形就越显著，即对其造成的总体损伤就越严重。
③
落石冲击速度并未改变曲线的线性段，这是因为曲线的线性段是由材料的屈服强度和hertz弹性接触理论共同决定的，不受落石冲击速度的影响。
[0236]
(2)落石半径
[0237]
这里取落石半径分别为0.25、0.5、0.75和1m，相应的落石质量分别为163.5、1308.3、4415.6和10466.7kg，其余参数均不变，由如图5所示的计算结果可以看出：
①
随着落石半径的增加，其质量也相应增加，进而导致其对钢筋混凝土桩板墙产生的最大冲击变形也由3.22mm逐渐增加到4.73、7.45和7.91mm，相应地最大冲击力也由0.54mn逐渐增加到1.53、3.64和5.03mn，这说明落石半径的增加对钢筋混凝土桩板墙造成的冲击力就越大，相应地产生的最大冲击变形也就越大；
②
随着落石半径的增加，钢筋混凝土桩板墙的残余变形则由1.71mm逐渐增加到2.10、3.45和3.15mm，即残余变形量总体上来说是增加的，但是当落石半径增加到一定程度后，就出现了反常，如落石半径为0.75m时的残余变形量反而大于落石半径为1m时的残余变形量，这说明随着落石质量的增加，落石对钢筋混凝土桩板墙的冲击损伤也将越来越严重，而这里是假定钢筋混凝土桩板墙的损伤演化规律是一定的，即式(9)中的δ
c
和γ两个损伤参数是不变的，因此这难免会带来一定误差。
[0238]
(3)钢筋混凝土桩板墙的损伤参数
[0239]
在本文的损伤模型中，主要有δ
c
和γ两个损伤参数，它们对计算结果的影响如图6所示，可以看出：
①
随着δ
c
的增加，钢筋混凝土桩板墙的冲击力
‑
变形曲线有一定的变化，但是其变化幅度较小，即当δ
c
由15mm逐渐增加到20、25和30mm时，钢筋混凝土桩板墙产生的最大冲击变形也仅由8.06mm逐渐降低到7.92、7.90和7.89mm，相应地最大冲击力也仅由4.947mn逐渐增加到5.005、5.022和5.024mn；同时钢筋混凝土桩板墙的残余变形也仅由3.24mm分别降低到3.15、3.1和3.1mm，这说明δ
c
的增加对钢筋混凝土桩板墙造成的冲击响应的影响较小，几乎可以忽略不计，另外由图6(a)也可以看出，这4条曲线也基本重合，这说
明δ
c
对计算结果的影响不大。
②
随着γ的增加，钢筋混凝土桩板墙的冲击力
‑
变形曲线的变化幅度迅速降低，即当γ由1逐渐增加到2、3和4时，钢筋混凝土桩板墙产生的最大冲击变形也由9.18mm逐渐降低到8.07、7.92和7.89mm，相应地最大冲击力也由4.4946mn逐渐增加到4.945、5.014和5.024mn；同时钢筋混凝土桩板墙的残余变形也由4.05mm分别降低到3.25、3.15和3.1mm，这说明γ的增加对钢筋混凝土桩板墙造成的冲击响应的影响先迅速增加，而后增加幅度迅速降低。同时由图6(b)也可以看出，当γ由1增加到2时，变化幅度最为显著，而后变化幅度则迅速减小。这是由于γ为损伤指数，而由式(9)可知，损伤的底数是小于1的，因为在本算例中损伤底数很小，因此当γ＝1时，损伤相对较大，因此对应的钢筋混凝土损伤也较大，曲线塑性段的斜率明显减小，残余变形也最大。而随着γ的增加，损伤的变化就相对较小，因而正如图6(b)所示，当γ＝2、3和4时，对应的3条曲线相差不大，基本重合。
③
通过对比δ
c
和γ两个损伤参数对计算结果的影响可以发现，相对而言，γ对计算结果的影响更为显著，尤其是当γ<2时，因此，在钢筋混凝土损伤试验中更应准确获得γ的试样值。
[0240]
综上实施例可见，本发明针对现有技术在多个方面的不足和问题，在经典接触理论的基础上，考虑落石冲击对钢筋混凝土桩板墙造成的损伤，提出考虑损伤接触理论并用于地质灾害工程实践；同时，根据落石冲击下钢筋混凝土桩板墙的动态响应过程，提出落石冲击下钢筋混凝土桩板墙的动态损伤模型，并对模型参数确定方法进行了延伸；最后，本发明进行了面向地质实践实例研究，显示落石冲击速度与半径对钢筋混凝土桩板墙的动态力学响应影响较大，而钢筋混凝土桩板墙的损伤参数δ
c
和γ对计算结果影响较小，但是当γ较小时，其影响较为显著；显示本发明能够很好地描述钢筋混凝土桩板墙在落石冲击下的动态力学行为，能够为工程设计提供高价值参考，具有十分良好的应用前景。
[0241]
以上所述实施例仅用以说明本发明的技术方案，而非对其限制；尽管参照前述实施例对本发明进行了详细的说明，本领域的普通技术人员应当理解：其依然可以对前述各实施例所记载的技术方案进行修改，或者对其中部分技术特征进行等同替换；而这些修改或者替换，并不使相应技术方案的本质脱离本发明各实施例技术方案的精神和范围，均应包含在本发明的保护范围之内。