一种基于图网络的集群动力学预测方法

本发明涉及深度学习技术领域，更具体地说，涉及一种基于图网络的集群动力学预测方法。

背景技术：

活性物质系统不受限于诸如细致平衡条件或涨落耗散定理等热力学规则，因而会涌现出丰富复杂的动力学现象，例如广泛存在于空间尺度的集群运动，在自然界中(例如，动物、微生物和细胞)，人类社会中(例如，集体性人类行为和社交网络)和多个体智能系统中(例如，多机器人系统和多车合作控制)都有很多例子。典型的集群运动模型能够模拟多种形式的物质的运动，包括鸟群和鱼群的运动。以集群运动行为作为研究对象的模型系统是一个由大量自治个体组成的集合，这些个体通过考虑邻居的影响和环境中的扰动因素进行更新，使其整体呈现出复杂的行为。在足够高的密度和低于某一临界值的噪音下，可以观察到集群的同步现象，理解这一现象背后的物理本质一直是软物质和非平衡统计物理领域一个重要的研究方向。

在过去的几年里，活性物质研究开始使用机器学习方法。将机器学习应用于科学研究的进展为活性物质研究提供了一个强大的工具，可以识别最优和替代策略、实现活性物质的分类和表征以及粒子的定位、追踪。强化学习和深度强化学习已被用于在模拟鱼群中寻找最小化能量消耗的游泳策略。然而，传统的机器学习在解决以上问题时，通常将图结构数据映射为简单的表示，这使预处理阶段可能丢失结构本身的拓扑信息，影响最终的预测结果。

综上所述，需要提供一种方法，充分从网络拓扑结构的角度考虑个体和邻居之间的局部相互作用力，无需经过复杂的分子动力学演化，仅从系统中粒子的初始位置就能预测动力学的相变过程。

技术实现要素：

本发明要解决的技术问题在于，针对现有技术中存在的不足，本发明提供一种基于图网络的集群动力学预测方法。

本发明解决其技术问题所采用的技术方案是：构造一种基于图网络的集群动力学预测方法，包括：

根据vicsek模型模拟自驱动集群运动，生成数据集；

通过数据预处理，将数据集处理为图结构数据,包括节点、边和全局属性；

实现特征的初步提取和数据降维；

使用图网络块，选择多层感知器作为更新函数，信息通过一定的规则在图上传播；

信息还原，得到图结构数据；

使用随机梯度下降的优化算法训练图网络，自动学习图网络中的参数。

其中，在vicsek模型中，n个可视为质点的个体以相同的速率在l*l的二维周期性边界条件的平面上运动，在初始时刻，每个个体的位置在该平面区域内随机分布，运动方向在[-π，π)间随机分布，在每一个时刻t+1，每个个体的角度依据邻居角度的矢量平均来更新，并且在其邻域内的平均运动方向添加了一些随机的扰动；

其中，在根据vicsek模型模拟自驱动集群运动的步骤中，邻居的定义采用如下公式表示：

ni(t)＝{j|dij(t)<r}

其中，ni(t)表示个体i在t时刻的邻居，r表示视野半径，dij(t)表示两个个体之间的距离；

每个个体在平面中始终以不变的速率v运动，位置变化采用如下公式：

其中θi(t)为个体i在t时刻运动的角度；

角度更新采用如下公式：

θi(t+1)＝<θi(t)>r+δθ

其中δθ代表以均匀概率从区间[-η/2，η/2]中选择的随机数，η表示环境中的噪音；<θi(t)>r为以个体i为圆心，视野半径r内所有个体(包含个体i自身)的平均速度方向；

计算视野半径r内所有个体(包含个体i自身)的平均速度方向采用如下公式：

其中，基于图网络的集群动力学预测网络由三个模块构成，分别为节点处理模块，边处理模块，全局状态处理模块；

其中，边处理模块用于对每一条边的状态进行更新，包含一个更新函数，根据给定边的特征，节点特征以及全局特征实现对于每条边的更新；

节点处理模块用于对每一个节点的状态进行更新，包含一个聚合函数和一个更新函数，利用聚合函数将节点周围的边的特征进行聚合，再基于节点特征和相关联的边特征的聚合，以及全局特征的影响，对节点进行更新；

全局状态处理模块用于对全局状态进行更新，包含两个聚合函数和一个更新函数，第一个聚合函数的接受参数为所有边的集合，第二个聚合函数的接受参数为所有点的集合，基于全局特征和所有节点的聚合以及边缘的聚合，实现对于全局的更新。

其中，三个处理函数中包含的更新函数实质上一种全连接神经网络的多层感知机，所述多层感知机由三层组成：

1)节点处理模块中的输入层的神经元数目为32，隐藏层的神经元数目为64，输出层的神经元数目为32；

2)边处理模块中的输入层的神经元数目为32，隐藏层的神经元数目为64，输出层的神经元数目为32；

3)全局状态模块中的输入层的神经元数目为32，隐藏层的神经元数目为64，输出层的神经元数目为1。

其中，聚合函数是对特征的求和。

与现有技术相比，本发明提供了一种基于图网络的集群动力学预测方法，包括：根据vicsek模型模拟自驱动集群运动，生成数据集；通过数据预处理，将数据集处理为图结构数据,包括节点、边和全局属性；实现特征的初步提取和数据降维；使用图网络块，选择多层感知器作为更新函数，信息通过一定的规则在图上传播；信息还原，得到图结构数据；使用随机梯度下降的优化算法训练图网络，自动学习图网络中的参数。通过本发明，能够实现对自驱动集群系统中的对象和关系进行模拟和推理，仅从初始粒子位置确定系统的长期演化，而不需任何手工特征。

附图说明

下面将结合附图及实施例对本发明作进一步说明，附图中：

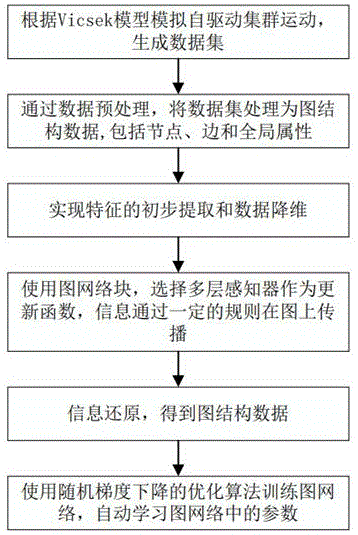
图1是本发明提供的一种基于图网络的集群动力学预测方法的步骤示意图。

图2是本发明提供的一种基于图网络的集群动力学预测方法的图网络模型图。

图3是本发明提供的一种基于图网络的集群动力学预测方法的图网络块结构图。

具体实施方式

为了对本发明的技术特征、目的和效果有更加清楚的理解，现对照附图详细说明本发明的具体实施方式。

如图1所示，本发明设计了一种基于图网络的集群动力学预测方法，包括：

根据vicsek模型模拟自驱动集群运动，生成数据集；

通过数据预处理，将数据集处理为图结构数据,包括节点、边和全局属性；

实现特征的初步提取和数据降维；

使用图网络块，选择多层感知器作为更新函数，信息通过一定的规则在图上传播；

信息还原，得到图结构数据；

使用随机梯度下降的优化算法训练图网络，自动学习图网络中的参数。

根据vicsek模型模拟自驱动集群运动，生成数据集，包括；

在vicsek模型中，n个可视为质点的个体以相同的速率在l*l的二维周期性边界条件的平面上运动，在初始时刻，每个个体的位置在该平面区域内随机分布，运动方向在[-π，π)间随机分布，在每一个时刻t+1，每个个体的角度依据邻居角度的矢量平均来更新，并且在其邻域内的平均运动方向添加了一些随机的扰动；

其中，邻居的定义采用如下公式表示：

ni(t)＝{j|dij(t)<r}

其中，ni(t)表示个体i在t时刻的邻居，r表示视野半径，dij(t)表示两个个体之间的距离；

每个个体在平面中始终以不变的速率v运动，位置变化采用如下公式：

其中θi(t)为个体i在t时刻运动的角度；

角度更新采用如下公式：

θi(t+1)＝<θi(t)>r+δθ

其中δθ代表以均匀概率从区间[-η/2，η/2]中选择的随机数，η表示环境中的噪音；<θi(t)>r为以个体i为圆心，视野半径r内所有个体(包含个体i自身)的平均速度方向；

计算视野半径r内所有个体(包含个体i自身)的平均速度方向采用如下公式：

通过数据预处理，将数据集处理为图结构数据,g＝(u，v，e),其中，g代表图，u代表全局的属性，v代表节点的属性，e代表边的属性，包括；

g是基于粒子之间的距离构建的，由于vicsek模型的视野半径为1，距离小于这个阈值的两个粒子通过边来连接。粒子的运动角度是节点的特征，粒子之间的相对距离是图的边缘的特征，每次迭代后的合速度是全局的特征。

实现特征的初步提取和数据降维，包括；

使用编码器(encoder)接收输入，输出特征向量，特征向量其实就是输入的特征和信息的另一种表示。

使用图网络块，选择多层感知器作为更新函数，信息通过一定的规则在图上传播，包括；

图网络块由三个模块构成，分别为节点处理模块，边处理模块，全局状态处理模块；

其中，边处理模块用于对每一条边的状态进行更新，包含一个更新函数，根据给定边的特征，节点特征以及全局特征实现对于每条边的更新；

节点处理模块用于对每一个节点的状态进行更新，包含一个聚合函数和一个更新函数，利用聚合函数将节点周围的边的特征进行聚合，再基于节点特征和相关联的边特征的聚合，以及全局特征的影响，对节点进行更新；

全局状态处理模块用于对全局状态进行更新，包含两个聚合函数和一个更新函数，第一个聚合函数的接受参数为所有边的集合，第二个聚合函数的接受参数为所有点的集合，基于全局特征和所有节点的聚合以及边缘的聚合，实现对于全局的更新。

其中，三个处理函数中包含的更新函数实质上一种全连接神经网络的多层感知机，所述多层感知机由三层组成：

1)节点处理模块中的输入层的神经元数目为32，隐藏层的神经元数目为64，输出层的神经元数目为32；

2)边处理模块中的输入层的神经元数目为32，隐藏层的神经元数目为64，输出层的神经元数目为32；

3)全局状态模块中的输入层的神经元数目为32，隐藏层的神经元数目为64，输出层的神经元数目为1。

其中，聚合函数是对特征的求和。

信息还原，得到图结构数据，包括；

使用解码器(decoder)抽取加工后的信息，还原为图结构数据。

使用优化算法训练图网络，自动学习图网络中的参数，包括；

用真实值和预测值之间的mae(平均绝对误差)和mse(均方误差)作为损失函数，使用优化算法对图网络进行训练，自动学习其中的参数。优化算法可以为基于梯度的优化算法，比如随机梯度下降方法、adam等等。

下面，如图2和图3所示，对本发明实施例进行进一步说明。

图网络作为深度学习的一个通用的模块化框架，可以被看作是以前基于图的神经网络的超集，graphnetwork(gn)的优点是它的通用性，如果目标问题的结构可以编码为图的形式，或者输入实体间关系的先验知识本身可以被描述为一张图，那么就可以用gn来分析。gn还具有很强的组合和泛化能力，gn块支持深度或递归排列，信息可以在图网络中进行传播，以允许更多信息来执行计算，实现复杂的功能。同时，计算不是在整个系统的宏观层面执行的，而是在各个实体和关系上复用的，这使得网络能够对未知数据集有很好的拟合结果。

本发明提供的一种基于图网络的集群动力学预测方法的图网络模型图如图2所示，为了实现特征提取和数据降维，在gn块前添加了编码器来预处理输入，发现这种方法提高了模型的训练速度和精度。在gn块中，分别用三个多层感知器实现对边、点和全局属性的更新，该块还添加了残差连接，用来解决在深层网络训练过程中的梯度爆炸和梯度消失问题。gn块循环n次，实现复杂的计算，并且用解码器将加工后的信息抽取出来，还原为图结构数据。在最后一步中，边、点和全局属性被连接并通过dense层以产生最终输出。

本发明公开的一种集群动力学预测的图网络块结构如图3所示，gn是图到图的函数，其输出图与输入图具有相同的节点和边缘结构。对于自驱动集群系统来说，这个图是基于个体之间的距离构建的，边是由粒子之间的相对距离定义的。一个gn块包含边、点和全局三个模块，这些模块由多层感知机组成，模块之间通过一定的规则进行关联，实现对图的更新。其中包括6个内部函数，三个更新函数和三个聚合函数。

首先，e′k边缘块为每条边计算一个输出，使用来自自身、其连接个体和全局状态的属性进行更新，如下所示：

其中，φ^e是边的更新函数。接下来，对于每一个顶点，顶点块将所有指向它的边聚合为，如下所示：

其中，ρ^e→v是指向每个接收节点的有向边的聚合函数，是所有指向索引为i的节点的有向边的集合，并计算每个节点的输出v′i，每个节点的属性通过使用自身的属性、连接到它的边和全局状态向量u来更新：

其中，φ^v是点的更新函数。接下来，在全局块中，边缘和节点级别的输出都被聚合以计算全局的特征：

其中，ρ^e→v是图上所有边的聚合函数，ρ^v→u是图上所有点的聚合函数，φ^u是全局属性的更新函数。因此，gn的输出是所有边缘、节点和图级特征的集合，g′＝(u′，v′，e′)。

更新函数φ^e，φ^v和的φ^u选择直接决定了模型在实际任务中的性能。在自驱动集群动力学图网络模型中，我们选择了多层感知器作为更新函数。

本发明构建了基于图网络的自驱动集群动力学模型，它将传统的物理科学与深度学习技术融合，可以实现对自驱动集群系统中的对象和关系进行模拟和推理，从而完成对系统的长期预测。

上面结合附图对本发明的实施例进行了描述，但是本发明并不局限于上述的具体实施方式，上述的具体实施方式仅仅是示意性的，而不是限制性的，本领域的普通技术人员在本发明的启示下，在不脱离本发明宗旨和权利要求所保护的范围情况下，还可做出很多形式，这些均属于本发明的保护之内。