一种超级电容器模组温度分布的在线估计方法

本发明涉及一种超级电容器模组温度分布的在线估计方法，该方法通过测量模组中少量单体的温度，在线估计超级电容器模组全部单体温度。

背景技术：

超级电容器作为一种新型储能器件，在可再生清洁能源发电、电动汽车节能运行、城市轨道和船舶等领域具有广阔的应用前景。随着超级电容器的工作，其内部温度的积累将使单体温度持续升高，影响其电气特性，导致性能下降，加速其老化进而缩短使用寿命。超级电容器温度过高或失控后还会造成整个系统的热失控，所以对超级电容器温度的在线估计尤为重要，有利于更加准确、高效地管理超级电容器，提高储能系统的安全性。

随着超级电容储能系统的广泛应用，在越来越多的应用场合中需要在线监测每一节超级电容器单体的温度。然而在实际应用中，受限于温度传感器的成本及安装等问题，往往只检测模组中少数单体的温度，不能实现对每节单体的温度监测。此外，对模组温度分布的研究一般使用有限元热仿真软件，但此方法模型复杂，会涉及到的计算量很大，计算时间较长，不利于在线运行。

技术实现要素：

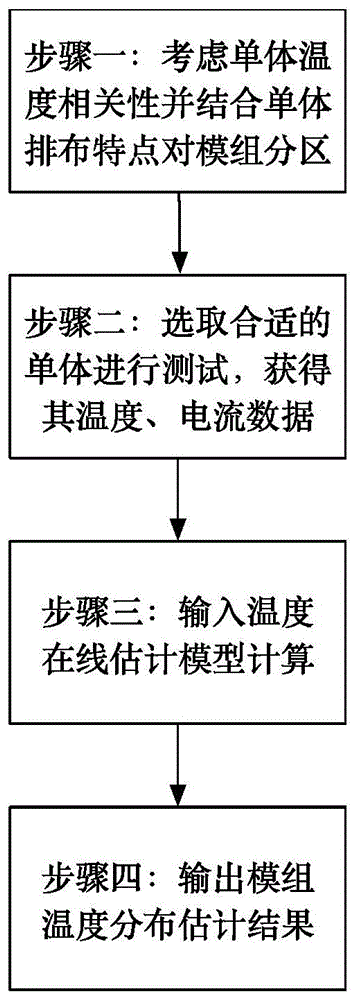
针对现有超级电容器模组温度估计方法中的不足，本发明提出一种可以有效利用少量单体温度估计模组中全部单体温度且计算流程简单的超级电容器模组温度在线估计方法。该方法结合模组中单体排布的特点，优化选取温度传感器安装位置，并考虑了超级电容器模组各单体之间的相关性，建立神经网络模型进行在线温度估计。方法实现流程如图1所示，其步骤为：

步骤一：考虑超级电容器模组内部单体温度的相关性，并结合单体的排布特点，对模组进行分区；

步骤二：根据分区选取被测单体进行测试，获得所选单体的温度、电流数据；

步骤三：构建神经网络模型，设计训练算法并训练优化建神经网络模型，得到估计模型，将测量得到的数据输入温度在线估计模型中计算；

步骤四：输出模组中各单体温度估计值。

步骤三中，神经网络模型采用基于levenberg-marquardt的算法进行训练，训练流程如下：

(1)初始化神经网络参数θ0，最大迭代数k，更新步长λ，步长缩减系数β，当前迭代数k＝0，训练误差限ε，早停初始值p＝0，早停耐心系数p；

(2)选择sigmoid函数作为激活函数计算神经网络前向传播其中，表示第m层第i个神经元的值，km-1表示第m-1层的神经元个数，表示第m-1层第j个输入神经元到第m层第i个神经元的权重，为第m层第i个神经元的偏置项。选择损失函数为其中，为样本i的误差平方，l为样本数；计算当前损失lossk，如果lossk＜ε，或k＞＝k，或p＞＝p，则转到第(5)步；

(3)按式θ＝θ-λ[j^t(θ)j(θ)+μi]^-1j^t(θ)e(θ)计算网络参数，其中，μ为大于零的常数，i为单位矩阵，j为jacobian矩阵；更新参数得到并计算更新一步参数后的模型损失值lossk+1；如果lossk+1＜lossk，则更新参数，令p＝0，k＝k+1，λ＝λ/β并转到第(2)步。否则转到第(4)步；

(4)令λ＝λβ，p＝p+1，转到第(2)步；

(5)输出t1、t2、t4、t5、t7、t8、t9单体估计的温度值。

与现有发明相比，本发明具有以下有益效果：

考虑了超级电容器模组中单体温度的相关性，通过少量温度测量值即可以有效估计超级电容器模组中全部单体的温度，大大减少了温度传感器的数量和安装成本。该方法流程简单，易于在线实现，具有很好的工程应用前景。

附图说明

图1为本发明方法流程图；

图2为本发明实施例超级电容器模组排布示意图；

图3为本发明实施例神经网络模型示意图。

具体实施方式

本方法具体执行过程如下：

步骤一中所述的模组分区方法以图2所示超级电容器模组为例进行说明。在无强制散热的条件下，考虑到模组的对称性，选取一半模组的9节单体为研究对象，分别标记为t1-t9。通过对超级电容器模组进行30a、50a、70a与90a恒流实验，可以发现受试单体温度分布主要分为三个区域。从每个单体的温度分布结果与超级电容器模组的排布方式可以分析得出，越靠近内部排列的单体温度上升速率越高，与其余单体接触面越多的单体温度上升速率越高。

实例中，如图所示：

t1与t3的温度最低，且与其余单体的接触面个数为2，因此可划为第一区域。

t2、t6、t7、t9、t4单体温度相近，与其余单体的接触面个数都为3，可划为第二区域。

t5与t8的温度最高，与其余单体的接触面个数为4，可划为第三区域。

步骤二中所述的测试单体的选择方法为：按照对算法精度和占用计算资源的要求，选择合理数量的单体进行测试，推荐每个温度分区中选取一个单体。在计算资源有限的情况下，可选择至少一个单体。本实例中选择t3和t6作为输入单体。

步骤三中所述的模组温度在线估计模型基于神经网络实现。将步骤二中选择的输入单体t3、t6的温度与电流i作为模组温度在线估计模型的输入，输出结果即为模组中其余单体t1、t2、t4、t5、t7、t8、t9的温度估计值，其精度与神经网络模型的结构以及训练样本的数量有关。通过离线训练神经网络模型，确定神经网络的结构，获得温度在线估计模型。本实例搭建的神经网络模型如图3所示，包括3个输入、7个输出以及中间先后2层隐藏层，隐藏层的神经元数量依次是28和14。

神经网络模型采用基于levenberg-marquardt的算法进行训练，levenberg-marquardt算法利用了误差的近似二阶梯度信息，在理论上比传统梯度下降法更为精确和高效。训练流程如下：

(1)初始化神经网络参数θ0，最大迭代数k，更新步长λ，步长缩减系数β，当前迭代数k＝0，训练误差限ε，早停初始值p＝0，早停耐心系数p。

(2)选择sigmoid函数作为激活函数计算神经网络前向传播其中，表示第m层第i个神经元的值，km-1表示第m-1层的神经元个数，表示第m-1层第j个输入神经元到第m层第i个神经元的权重，为第m层第i个神经元的偏置项。选择损失函数为其中，为样本i的误差平方，l为样本数。计算当前损失lossk，如果lossk＜ε，或k＞＝k，或p＞＝p，则转到第(5)步。

(3)按式θ＝θ-λ[j^t(θ)j(θ)+μi]^-1j^t(θ)e(θ)计算网络参数，其中，μ为大于零的常数，i为单位矩阵，j为jacobian矩阵。更新参数得到并计算更新一步参数后的模型损失值lossk+1。如果lossk+1＜lossk，则更新参数，令p＝0，k＝k+1，λ＝λ/β并转到第(2)步。否则转到第(4)步。

(4)令λ＝λβ，p＝p+1，转到第(2)步。

(5)输出t1、t2、t4、t5、t7、t8、t9单体估计的温度值。

本实施例只是本发明的较优实施方式，需要说明的是，在不背离本发明精神及其实质的情况下，熟悉本领域的技术人员当可根据本发明作出各种相应的改变和变形，但这些改变和变形都应属于本发明所附的权利要求的保护范围。