应用于循环神经网络的激活函数的可重构电路

本发明涉及集成电路技术领域，尤其涉及一种应用于循环神经网络的激活函数的可重构电路。

背景技术：

为提高人工神经网络的计算效率，asic(专用集成电路)硬件实现是对其加速的主要途径。双曲函数(tanh和sigmoid)是常用的神经网络激活函数，特别是在处理具有时序信息的循环神经网络(rnn)以及它的变种网络：长短期记忆网络(lstm)和循环门控单元(gru)中。但因为双曲函数中包含幂运算和除法运算，使其成循环神经网络硬件化过程中的难点之一。

现有的双曲函数硬件化方法主要有：查找表(lut)法、cordic法、分段线性近似(pwl)法、分段非线性近似法以及混合法。查找表法是最直接的方法，但要实现高精度。则需要较大的存储空间，在大规模的网络加速中迫于片上存储压力，lut并不适用。cordic法使用的硬件资源少，但需要多个周期的迭代计算才可获得高精度。两种分段近似的方法具有相似性，分段数越多，近似函数精度越高。相比于分段线性，分段非线性近似法由于其非线性特性，具有分段少、精度高的优点，但其消耗硬件资源多。

在实现本发明构思的过程中，发明人发现相关技术中至少存在如下问题：现有技术的这些方法在实现tanh函数和sigmoid函数时，均要针对两种函数设计两套不同的电路，不能实现二者的重构复用，徒增硬件资源和设计成本。并且当前循环神经网络硬件加速中多采用8比特数据，网络推理精度对激活函数精度敏感。一个高精度适用于8比特循环神经网络加速器的，激活函数硬件实现方案是有必要的。

技术实现要素：

有鉴于此，本发明的主要目的在于提供一种应用于循环神经网络的激活函数的可重构电路，以期部分地解决上述技术问题中的至少之一。

为了实现上述目的，本发明提供了一种应用于循环神经网络的激活函数的可重构电路，包括原码转换电路、一比特移位器、二比特移位器、第一选择器、第一反相器、误差补偿单元、乘法器单元、第二选择器、第二反相器和镜像电路；其中，

待处理数据输入所述原码转换电路，输出为输入数据的二进制原码形式，将原码转换电路的输出数据输入所述一比特移位器和所述二比特移位器，将两个比特移位器的输出数据输入所述第一选择器，根据模式选择信号select选择数据的移动位数；在所述第一选择器之后采用所述第一反相器对数据进行取反操作，经过第一反相器之后的数据输入所述乘法器单元，计算经过第一反相器之后的数据的平方值；接着，输入所述第二选择器，根据模式选择信号select选择所述乘法器单元计算结果的移动位数，在所述第二选择器之后用所述第二反相器对数据进行取反操作；最后将上述最终结果输入所述镜像电路，用于镜像计算函数自变量负半轴的函数值，进而获得完整的定义域上的函数值。

其中，所述可重构电路适用于8比特循环神经网络加速器的高精度激活函数计算电路。

其中，所述误差补偿单元用于根据原码所在值域范围对函数计算值进行误差补偿，补偿值以达到提高精度的目的。

其中，所述一比特移位器是将输入值右移一比特；所述二比特移位器是将输入值右移二比特。

其中，所述第一选择器包括两种计算模式的选择；如果模式选择信号select为1，选择sigmoid函数计算模式，数据向右移动2比特；如果模式选择信号select为0，选择tanh函数计算模式，数据向右移动1比特。

其中，所述第二选择器包括两种计算模式的选择；如果模式选择信号select为1，选择sigmoid计算模式，数据向右移动1比特；如果模式选择信号select为0，选择tanh计算模式，数据不移动。

其中，所述镜像电路包括具有奇函数性质的tanh函数镜像和类奇函数的sigmoid函数镜像。

其中，所述误差补偿单元包括依据精度要求的误差补偿区间划分方式。

其中，以二阶近似为基础的硬件友好的sigmoid函数近似表达式如下式所示：

其中，以二阶近似为基础的硬件友好的tanh函数近似表达式如下式所示：

基于上述技术方案可知，本发明的可重构电路相对于现有技术至少具有如下有益效果的一部分：

(1)本发明采用重构复用的方式，以同一套电路结构，实现两种不同的激活函数，节省了硬件资源。

(2)本发明针对8比特数据位宽，进行误差补偿设计，可实现更高的计算精度。

(3)本发明的循环神经网络激活函数不占用片上存储资源，面积小，功耗低，可用于大规模网络加速器的设计中。

附图说明

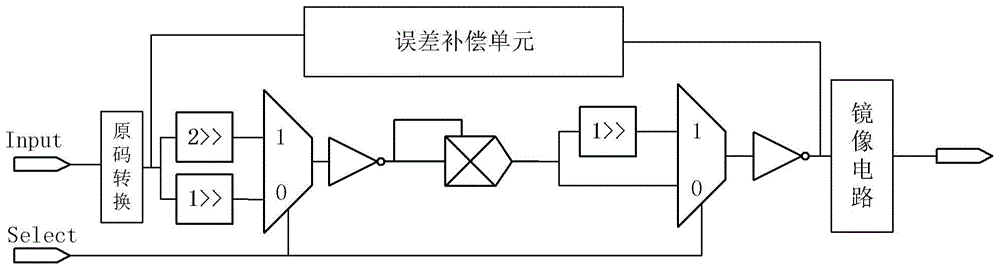
图1为本发明实施例提供的应用于循环神经网络的激活函数可重构设计结构示意图；

图2为本发明实施例提供的镜像电路的结构示意图；

图3为本发明实施例提供的sigmoid函数和tanh函数正半轴近似电路结构对比图；

图4为本发明实施例提供的误差补偿区间划分示意图；

图5为本发明实施例提供的sigmoid近似函数图像及误差曲线；

图6为本发明实施例提供的tanh近似函数图像及误差曲线。

具体实施方式

为使本发明的目的、技术方案和优点更加清楚明白，以下结合具体实施例，并参照附图，对本发明作进一步的详细说明。

本发明公开了一种用于循环神经网路的激活函数的可重构电路，是适用于8比特循环神经网络加速器的高精度激活函数计算电路，本发明结构简单，硬件资源消耗少，精度高，易于直接嵌入循环神经网络加速器中。

如图1所示，为应用于循环神经网络的激活函数可重构设计结构示意图；使用电路设计中的分时复用技术，对循环神经网络中的激活函数进行可重构设计。其包含：原码转换电路、一比特移位器、二比特移位器、第一选择器、误差补偿单元、乘法器单元、第二选择器、镜像电路和必要的反相器。

原码转换电路：将输入值转换成二进制原码形式，即对于互为相反数的自变量值，只有符号位不同。

一比特移位器：将输入值右移一比特，即计算2^-1x。

二比特移位器：将输入值右移二比特，即计算2^-2x。

第一选择器：根据模式选择信号select选择数据的移动位数，亦是计算模式的选择。如果模式选择信号select为1，选择sigmoid函数计算模式，数据向右移动2比特；如果模式选择信号select为0，选择tanh函数计算模式，数据向右移动1比特。

在第一选择器之后用反相器对数据进行取反操作，这里的取反操作是代替了(1-2^-nx)(n＝1或2)中的减法操作，以减少硬件资源的消耗；乘法器单元：用于计算经过反相器之后的数据的平方值。

第二选择器：根据模式选择信号select选择乘法器单元计算结果的移动位数，亦是计算模式的选择。如果模式选择信号select为1，选择sigmoid计算模式，数据向右移动1比特，即计算2^-1(1-2^-2x)²；如果模式选择信号select为0，选择tanh计算模式，数据不移动。

在第二选择器之后用反相器对数据再次进行取反操作。即计算1-2^-m(1-2^-nx)²(m＝1或0，n＝1或2)。

至此完成的是sigmoid函数和tanh函数自变量正半轴的电路结设计。

本实施例的循环神经网络激活函数输出位宽为8比特(1比特的符号位，7比特的小数位)。在循环神经网络中，激活函数之前是大量的矩阵向量乘法，数据位宽被拓展，因此激活函数输入位宽可根据精度要求灵活调整。依据sigmoid函数和tanh函数一阶导数，以及二者在零点附近的极限值，可知输入数据的小数位宽至少为8。输入数据的整数位宽根据输入值的范围进行灵活调整。sigmoid函数关于(0，0.5)点对称，tanh函数关于(0，0)点对称，在硬件设计时，先实现自变量正半轴的函数值计算，负半轴通过镜像正半轴函数值来获取。基于最小二乘法，使用python分别对sigmoid函数和tanh函数进行二阶拟合，并通过log2变换，可以得到硬件友好的二阶近似函数。

以二阶近似为基础的硬件友好的sigmoid函数近似计算表达式：

以二阶近似为基础的硬件友好的tanh函数近似计算表达式：

对于正半轴，即x＞0时，sigmoid函数和tanh函数近似电路结构如图3所示。在图3中，上半部分为sigmoid函数近似电路结构，下半部分为tanh函数近似电路结构。可直观发现二者的重复结构，即图3中虚线框部分所示。重复结构是反相器和乘法器，其为sigmoid函数和tanh函数近似电路的主要资源消耗部分。

为了完整计算全定义域上的函数值，在其后增加镜像电路模块。镜像电路：用于镜像计算函数自变量负半轴的函数值。镜像电路结构如图2所示，首先对正半轴电路计算值进行取反加一的操作，得到正半轴计算值相反数的二进制补码的。如果模式选择信号select为0，选择tanh函数计算模式，直接输出二进制补码。如果模式信号select为1，选择的sigmoid函数计算模式，此时不能直接将二进制补码输出。因为sigmoid函数关于(0，0.5)点对称，且函数值非负，若直接取二进制补码输出，输出值与实际值绝对值差1。所以，将sigmoid计算模式下的二进制补码的最高位：符号位取反，即可得到sigmoid函数自变量处于负半轴时的函数值。

误差补偿单元：用于根据原码所在值域范围对函数计算值进行误差补偿，补偿值以达到提高精度的目的。误差补偿区间划分示意如图4所示。对sigmoid和tanh近似函数的误差曲线分别进行如下划分，以获取补偿区间和补偿值。首先对误差曲线进行横向的切分(图4中横向虚线所示)，切分间距δε是近似函数的目标精度(亦最大绝对误差)，再根据切分线与误差曲线的交点，确定补偿区间和补偿值。例如，图4中，横向切分线与误差曲线的交点分别为a，b，对应的横坐标为xi，xi+1，则补偿区间为x∈(xi，xi+1)，补偿值为2δε。

sign信号是符号位，用于选择输出结果是自变量正半轴的函数值或是自变量负半轴的函数值。当sign为1，表示自变量为负数，输出函数值选择负半轴镜像的结果；当sign为0，表示自变量为正数，输出函数值选择正半轴计算结果。

图5上部分是sigmoid近似函数图像、下部分是误差曲线划分及误差补偿之后误差曲线。图6上部分是tanh近似函数图像、下部分是误差曲线划分及误差补偿之后误差曲线。

以上所述的具体实施例，对本发明的目的、技术方案和有益效果进行了进一步详细说明，应理解的是，以上所述仅为本发明的具体实施例而已，并不用于限制本发明，凡在本发明的精神和原则之内，所做的任何修改、等同替换、改进等，均应包含在本发明的保护范围之内。