一种适用于纹理贴图的浮雕网格重构方法

本发明属于计算机辅助设计、工业设计制造技术领域，涉及一种适用于纹理贴图的浮雕网格重构方法。

背景技术：

将图片转化为模型上三维浮雕网格常见的方法是先将网格等面积重构，细分，然后通过建立模型顶点与图像像素的映射，调整顶点位置以实现浮雕网格重构。然而这种方法会生成很多不必要顶点，不仅影响浮雕网格重构效率，浪费计算机存储空间，而且精度上不够高，影响浮雕网格效果。

本发明提出的适用于纹理贴图的浮雕网格重构方法具有实现容易，效率高，效果好等诸多优点，非常适用于浮雕网格建模。

技术实现要素：

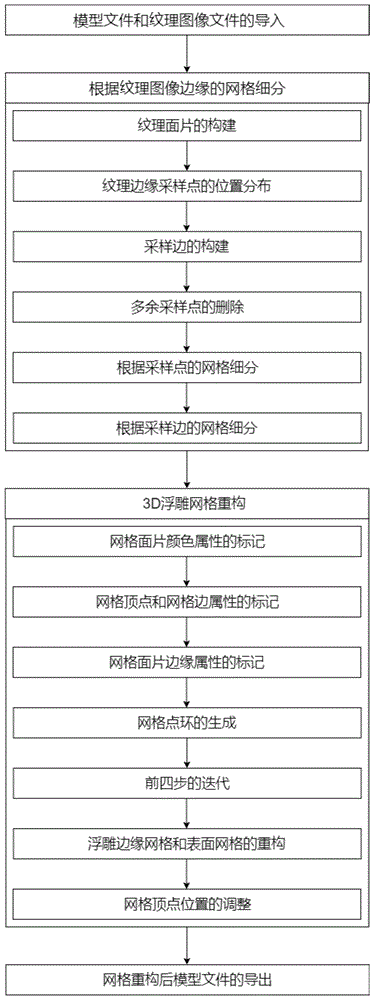
为解决上述问题，本发明提出一种适用于纹理贴图的浮雕网格重构方法，流程如图1所示。首先，根据导入的纹理图像边缘采样，对由导入的模型文件数据构建的三角网格，进行网格细分。然后，通过网格生成，重构浮雕边缘网格和浮雕表面网格。最后导出网格重构后的模型文件，完成浮雕网格重构。

本发明的技术方案：

一种适用于纹理贴图的浮雕网格重构方法，步骤如下：

(1)根据纹理图像边缘的网格细分

(1.1)纹理面片的构建

根据面片f1,f2......fnf构建对应的纹理面片集合uvf1＝{uvf1,uvf2......uvfnf}，其中，fa与uvfa一一映射，1≤a≤nf,a∈n+；nf为初始网格面片最大索引值；uvfa顶点坐标为fa顶点uv坐标；

(1.2)纹理边缘采样点的位置分布

第一步，根据uvf1,uvf2......uvfnf分割纹理，得到纹理集合s1＝{s1,s2......snf}，其中uvfa与sa一一映射；sa具体参数如下：

其中，为uvfa三个顶点坐标中u轴坐标最大值；为uvfa顶点坐标中v轴坐标最大值，为上述uv坐标中u轴最小值；为上述uv坐标中v轴最小值；为sa的宽度；为sa的高度；为sa左上角坐标相对于纹理图像t左上角坐标的偏移量；twidth为t宽度，theight为t高度；

第二步，分别对s1,s2......snf进行查找边缘；对于sa，查找边缘后得到轮廓集合sva＝{sva1,sva2......svaα}，且svab＝{svab1,svab2......svabβ}；其中，sa与sva一一映射；svab为sva中第b个轮廓采样点序列，且1≤b≤α，α为轮廓数量；svabc为svab中第c个采样点，且1≤c≤β，β为svab中采样点数量；svabc在t上坐标为计算过程如下：

其中，为svabc在sa上像素坐标；为sa左上角坐标相对于纹理图像t左上角坐标的偏移量；

第三步，判断采样点位置；分别判断与s1,s2......snf对应的轮廓集合sv1,sv2......svnf中的采样点集中采样点相对于面片和网格边的位置，并建立边上采样点集合soe＝{soe1，soe2......soene}，soed＝{soev1,soev2......soevnse}，其中ed与soed一一映射，1≤d≤ne；ne为初始网格边最大索引值；nse为soed中采样点数量；建立面片上采样点集合sof＝{sof1，sof2......sofnf}，sofa＝{sofv1,sofv2......sofvnsf}，其中fa与sofa一一映射，nsf为sofa中采样点数量；

(1.3)采样边的构建

通过采样点得到采样边集合se＝{se1,se2......senf}，seg＝{seg1,seg2......segsne}；其中，sea与sa一一映射，即sea为根据sa中采样点位置得到的采样边集合；segh为第h个插入seg的采样边，1≤h≤sne，sne为seg中采样边数量；

(1.4)多余采样点的删除

对于所有采样点，利用分治法，删除位置相同或两点之间欧式距离小于εv的采样点中的一个；

(1.5)根据采样点的网格细分

第一步，依次对面片f1,f2......fnf引入变量ancestor，并将ancestor赋值为面片索引，fa的ancestora为a，ancestora表示fa的ancestor；

第二步，按照如下步骤进行网格细分：

1)依次遍历soe1,soe2......soecne1，对于每一个集合，找到soep中与ep中点的欧式距离最小的采样点soevdismin，其中，dismin取值唯一且1≤dismin≤nse；cne1为变量，随网格边索引最大值变化而变化，值始终与当前网格边索引最大值相等，初始值为ne；1≤p≤cne1,p∈n+；根据soevdismin的几何信息和ep顶点几何信息计算插值，在网格中生成新的顶点vnewk，其中，newk为生成新顶点后网格顶点最大索引值，然后对ep引入分割点变量splitvertex，将vnewk赋值予splitvertexp，splitvertexp表示与ep对应的分割点变量；

2)构建面片集合wsf1：

①依次遍历f1,f2......fcnf1，对于每个面片，如果三条边中的任意一条边包含变量splitvertex，将该面片插入wsf1；其中，cnf1随网格面片索引最大值变化而变化，值始终与当前网格面片索引最大值相等，初始值为nf；

②依次遍历wsf1中面片元素，直至所有元素被遍历；对于fi，如果上不包含则计算中点插值，在网格上生成新的顶点vnewi，其中，1≤i≤cnf1,i∈n+,fi∈wsf1；longest表示该边为fi最长边，为fi的最长边；为的分割点变量；newi为生成新顶点后网格顶点数量；然后，对引入变量将vnewi赋值予接着，删除asi中与vnewi的uv坐标的欧式距离小于εv的采样点，并将以这些采样点为端点的采样边的对应端点坐标替换为vnewi的uv坐标，其中分别为与fi三条边对应的soe中的采样点集合；最后，如果另一个以为边的三角面片没有在wsf1中，则将其插入wsf1；

③依次遍历wsf1中面片元素，根据各面片边上splitvertex建立拓扑关系，细分网格，具体步骤如下：

a.如果面片中有且只有1条边上有splitvertex，以splitvertex和不含splitvertex的两条边的公共顶点为端点，构建新边，将三角面片分割为2个新面片；如果面片中有且只有2条边上有splitvertex，连接两个splitvertex，构成第一条新边；因为连接splitvertex和另外两条边公共顶点有两种情况，所以比较这两种情况下新建边的长度，选取更短的情况构成第二条新边；新建的两条新边将面片分为3个新面片；如果面片中有3条边上有splitvertex，依次连接三个splitvertex，构成三条新边，将三角面片分割为4个新面片；

b.将a的取值范围改为1≤a≤cnf1,a∈n+；将d的取值范围改为1≤d≤cne1,d∈n+；

c.对于每一个面片，将被分割前与该面片对应的sof中的采样点集合和与该面片三条边分别对应的soe中的采样点集合中的采样点分配到与新面片对应的采样点集合和与新网格边对应的采样点集合，并分别插入sof，soe；

d.对于每一个面片，将面片ancestor变量值赋予通过分割该面片得到的新面片的ancestor变量；

4)重复步骤1)—3)，直至soe1,soe2......soecne1都变为空集；然后遍历sof1,sof2......sofcnf1，直至找到一个采样点集合不为空集，具体步骤如下：

①找到该集合中与该集合对应的纹理面片重心的欧式距离最小的采样点元素，将采样点从集合中删除，并根据该采样点与该纹理面片对应的网格面片顶点几何信息计算插值，在网格上生成新的顶点vnewa；其中，newa为新顶点生成后网格顶点最大索引值；

②将vnewa与面片顶点分别连接，构成三条新边，将面片分割为三个新面片；

③将a的取值范围改为1≤a≤cnf1,a∈n+；将d的取值范围改为1≤d≤cne1,d∈n+；

④对于每一个被分割面片，将被分割前与该面片对应的sof中的采样点集合中的采样点元素，分配到与新面片对应的采样点集合和与新网格边对应的采样点集合，并分别将这些集合插入soe和sof；

⑤对于每一个被分割面片，将面片ancestor变量值赋予通过分割该面片得到的新面片的ancestor变量；

5)重复步骤1)—4)，直至soe1,soe2......soecne1，sof1,sof2......sofcnf1都变为空集；

(1.6)根据采样边的网格细分

第一步，根据ancestor变量建立af＝{af1,af2......afnf}，afj＝{fk|(ancestork＝j)∧(1≤k≤cnf2∧k∈n+)}，其中，1≤j≤nf,j∈n+；cnf2随网格面片索引最大值变化而变化，值始终与当前网格面片索引最大值相等；

第二步，计算采样边与网格边的相交情况，细分网格；依次遍历af中每个集合，对于每一个af集合，具体步骤如下：

1)构建边集ae，依次遍历集合中的面片元素，对于面片的各条边，如果以该边为边的两个面片的ancestor值都与集合对应的ancestor值相同，则将该边插入集合ae，其中ae中元素不重复；

2)依次遍历se中与该面片集合对应的采样边集合中的采样边元素，细分网格；对于每一条采样边元素，具体步骤如下：

①根据采样边端点坐标和网格边顶点uv坐标将采样边和ae中网格边元素转至普吕克坐标系；

②建立网格边集合inserte；依次遍历ae中各网格边，在普吕克坐标系下，计算网格边与采样边是否相交，如果相交，将该网格边插入集合inserte；

③依次遍历inserte中网格边元素，根据交点生成网格顶点，建立wsf2集合，对于每条网格边，根据该网格边顶点和该采样边端点几何信息，计算网格边与采样边交点的几何信息，并在网格上生成新的顶点vnewb；其中，newb为新顶点生成后网格顶点最大索引值；将vnewb赋值予网格边的splitvertex变量；将以该网格边为边的面片插入wsf2；

④依次遍历wsf2中面片元素，进行网格细分；细分方式与(1.5)的2)中③相同；

⑤将通过本次细分得到的新的网格边插入ae；

(2)3d浮雕网格重构

(2.1)网格面片颜色属性的标记

第一步，根据面片构建对应的纹理面片集合其中，cnf3为变量，随网格面片索引最大值变化而变化，值始终与当前网格面片索引最大值相等；

第二步，根据分割纹理，得到纹理集合具体参照(1.2)第一步；

第三步，根据纹理图像像素值，二值化为0和255，判断面片的颜色属性，依次遍历对于每个纹理面片，具体步骤如下：

1)分别将纹理面片顶点坐标转至与该纹理面片对应的s中的图像像素坐标系下；

2)在图像坐标系下，遍历位于纹理面片内部的像素点，如果像素值为0的像素点数量占所有位于纹理面片内部的像素点数量的εcolor，则将该面片标记为blackface；同理，如果像素值为255的像素点数量占εcolor，则将该面片标记为whiteface；εcolor取90％，因误差等因素，可逐渐降低εcolor，直至判断面片颜色属性；

(2.2)网格顶点和网格边属性的标记

第一步，标记网格边和顶点的边缘属性；遍历其中，cne3为变量，随网格边索引最大值变化而变化，值始终与当前网格边索引最大值相等；对于每条网格边，如果以该网格边为边的两个三角面片的颜色属性不一致，则将该网格边标记为boundaryedge，同时将该网格边的两个端点标记为boundaryvertex；

第二步，标记网格顶点的颜色属性；遍历其中，cnv3为变量，随网格顶点索引最大值变化而变化，值始终与当前网格顶点索引最大值相等；对于每个网格顶点，如果该顶点没有被标记为boundaryvertex，说明该顶点的一阶领域三角面片颜色属性相同，且该顶点与一阶领域三角面片颜色属性相同，比如该顶点的一阶领域三角面片颜色属性为blackface，则将该顶点标记为blackvertex；

(2.3)网格面片边缘属性的标记

标记网格面片边缘属性，依次遍历面片对于每个面片，具体步骤如下：

1)依次遍历该面片三个顶点，如果三个顶点都没有被标记为boundaryvertex，则将该面片标记为notboundaryface；如果至少有一个顶点被标记为boundaryvertex，继续执行(2.3)的2)；

2)依次遍历该面片三条边，有以下3种标记情况：

①没有边被标记为boundaryedge，且该面片颜色属性为blackface，则将该面片标记为boundaryinface；

②没有边被标记为boundaryedge，且该面片颜色属性为whiteface，则将该面片标记为boundaryoutface；

③至少有一边被标记为boundaryedge，则将该面片标记为boundaryface；

(2.4)网格点环的生成

根据浮雕边缘网格顶点拓扑信息，生成网格点环，具体步骤如下：

1)建立网格边不重复集合ringedge，网格顶点集合ringvertex，依次遍历对于每个网格顶点，如果以该顶点为端点的网格边中，有大于两条网格边被标记为boundaryedge，将该顶点插入ringvertex；

2)生成网格顶点；依次遍历ringvertex中网格顶点元素，对于每一个网格顶点，遍历以该顶点为端点的所有网格边，对于每一条网格边，在距离(欧式距离)该顶点dist的网格边上计算插值，生成网格顶点vnewd；其中，newd为生成新顶点后网格顶点最大索引值；dist取该网格边长度的εring，εring取2.0*10^-5；将vnewd赋值予该网格边的splitvertex变量；

3)生成网格拓扑信息；依次遍历ringvertex中网格顶点元素，对于每一个顶点，具体步骤如下：

①遍历该顶点的一阶领域三角面片，对于每一个面片，根据网格顶点，建立拓扑信息：

以该顶点为起始顶点，逆时针遍历该面片顶点，分别赋予临时别名v¹,v²,v³；以v¹和v²为端点的网格边splitvertex变量值称为splitvertex¹，以v¹和v³为端点的网格边splitvertex变量值称为splitvertex²；

连接splitvertex¹和splitvertex¹，构成第一条新网格边；连接splitvertex¹和v²，构成第二条新网格边；该面片被分割为三个新面片；

②标记新面片的颜色属性；将该顶点的一阶领域三角面片标记为whiteface；该顶点的二阶领域三角面片标记为母面片颜色属性；

(2.5)(2.1)-(2.4)的迭代

清除网格顶点，边，面片的边缘属性，迭代进行(2.1)-(2.4)，直至所有网格顶点都满足：以该顶点为端点的所有网格边中，有不超过2条被标记为boundaryedge；

(2.6)浮雕边缘网格和表面网格的重构

第一步，根据被标记为boundaryvertex生成新的网格顶点；具体步骤如下：

1)建立集合boundarysetvertex；将中，被标记为boundaryvertex的顶点插入boundarysetvertex；其中cnv4随网格顶点索引最大值变化而变化，值始终与当前网格顶点索引最大值相等；

2)生成新的网格顶点；依次遍历boundarysetvertex中顶点元素，对于每个网格顶点，根据该顶点几何信息，生成新的网格顶点vnewe，其中，newe为生成新顶点后网格顶点最大索引值，vnewe的几何信息计算过程如下：

其中，其中分别为vnewe的模型坐标和uv坐标；分别为该顶点的模型坐标和uv坐标；为该顶点的归一化法线坐标；εrelief在网格归一化的情况下取0.1；为该顶点引入变量above，并将vnewe赋值予above；

3)根据网格顶点，建立拓扑信息；具体步骤如下：

①建立浮雕边缘拓扑信息；首先建立boundarysetedge；依次遍历e＝{e1,e2......ecne4}，其中cne4随网格边索引最大值变化而变化，值始终与当前网格边索引最大值相等；对于每一条网格边，如果该网格边被标记为boundaryedge，将该网格边插入集合boundarysetedge；

依次遍历boundarysetedge中网格边元素，对于每一条网格边，暂称以该网格边为边并且颜色属性为blackface的三角面片为f^b，以f^b中非该网格边端点的顶点为起点，逆时针遍历，先遍历到的顶点(不包含起点)称为ev¹，后遍历到的称为ev²；

新建面片fnew1,fnew2，fnew1的顶点为above1,ev¹,above2；fnew2的顶点为above2,ev¹,ev²；其中，above1,above2分别为ev¹,ev²的above值；new1，new2分别为生成新面片后网格面片最大索引值；

②创建浮雕表面拓扑信息；首先，创建集合reliefface；依次遍历其中，cnf4为当前网格面片最大索引值；将被标记为boundaryinface和boundaryface的面片插入reliefface；接着，依次遍历reliefface中的面片元素，对于每个面片，依次遍历该面片的顶点，如果顶点有变量above且above不为空值，则用above值替代该顶点成为新的顶点，所有顶点更改后构成新面片，删除原面片；

(2.7)网格顶点位置的调整

依次遍历所有没有被标记为boundaryvertex且颜色属性为blackvertex的网格顶点，对于每个顶点，该顶点新的模型坐标vnewpos计算过程如下：

vnewpos＝vpos+εrelief*vnormal(2.3)

其中，vpos为该顶点未调整前的模型坐标；vnormal为该顶点的归一化法线坐标；εrelief在网格归一化的情况下取0.1就得到凸出明显的浮雕。

本发明的有益效果：本发明提出一种适用于纹理贴图的浮雕网格重构方法，通过适用于纹理图像信息的网格细分，网格生成，重构了浮雕边缘网格和浮雕表面网格。通过本发明重构浮雕网格，过程简洁，细节突出，效果精细。与普通网格重构方法相比，该方法减少了不必要顶点的生成，效率更高，而且能展现浮雕更多的细节，效果更好。

附图说明

图1是本发明的流程图。

图2(a)是用于构建图2(b)纹理面片的网格面片示意图。

图2(b)是由图2(a)网格面片构建的纹理面片示意图。

图3是网格边细分示意图。

图4(a)是网格边细分(新建边长于图4(b))示意图。

图4(b)是网格边细分(新建边短于图4(a))示意图。

图5是网格边细分示意图。

图6是网格面片细分示意图。

图7是点环生成网格边细分示意图。

图8(a)是点环生成(网格重构前)示意图。

图8(b)是点环生成(网格重构后)示意图。

图9是浮雕边缘的网格重构示意图。

图10是浮雕表面的网格重构示意图。

图11(a)是输入纹理示意图。

图11(b)是三维雕刻结果示意图。

图11(c)是三维雕刻结果(侧面角度)示意图。

图11(d)是三维雕刻结果(不同渲染)示意图。

图11(e)是带有纹理贴图的三维浮雕结果示意图。

具体实施方式

以下结合附图和技术方案，进一步说明本发明的具体实施方式。

一种适用于纹理贴图的浮雕网格重构方法，具体可分为导入模型文件和图像文件；根据导入的纹理图像边缘采样点，对由导入的模型文件数据构建的三角网格，进行网格细分；通过网格生成，重构浮雕边缘网格和浮雕表面网格；导出网格重构后的模型文件这四个主要步骤：

(一)模型文件和图像文件的导入

以m模型和p图像为例。

可以使用assimp等库读取m模型文件(obj，stl等)，并使用半边数据结构存储m模型网格数据。根据模型文件数据构建三角网格，三角网格m由(v,e,f)表示，其中v＝{v1,v2......vnv}为网格顶点集合，e＝{e1,e2......ene}为网格边集合，f＝{f1,f2......fnf}为网格面片集合。其中，nv表示初始网格顶点索引最大值；ne表示初始网格边索引最大值；nf表示初始网格面片索引最大值。

可以使用opencv等库读取p图像文件(bmp，png等)，并将图像灰度化后二值化，像素灰度值为0或255。二值化后的p图像称为图像t。t的宽度为twidth，高度为theight。

(二)根据图像t边缘的格细分

根据面片f1,f2......fnf构建对应的纹理面片集合uvf＝{uvf1,uvf2......uvfnf}，其中fi与uvfi一一映射，1≤i≤nf,i∈n+。

如图2，fi顶点为uvfi顶点为其中，坐标为的uv坐标坐标为的uv坐标坐标为的uv坐标为边顶点；为边顶点；为边顶点。

接着，根据uvf1,uvf2......uvfnf分割纹理，得到纹理集合s1＝{s1,s2......snf}，其中uvfi与si一一映射。si具体参数如下：

其中，为面片uvfi顶点的坐标中u轴坐标最大值；为面片uvfi顶点的uv坐标中v轴坐标最大值。同理，为上述uv坐标中u轴最小值；为上述uv坐标中v轴最小值。为si的宽度；为si的高度；为si左上角坐标相对于t左上角坐标的偏移量。

接着，可以使用opencv等库分别对s1,s2......snf进行查找边缘，以si为例，查找边缘后得到轮廓集合svi＝{svi1,svi2......sviα}，且svij＝{svij1,svij2......svijβ}。其中，si与svi一一映射，svij为svi中第j个轮廓采样点序列，且1≤j≤α，α为轮廓数量；svijk为svij中第k个采样点，且1≤k≤β，β为svij中采样点数量。svijk在t上坐标为计算过程如下：

其中，为svijk在si上像素坐标。为si左上角坐标相对于t左上角坐标的偏移量。

接着，判断采样点位置。分别判断s1,s2......snf的轮廓集sv1,sv2......svnf中的采样点集中采样点的位置，并建立边上采样点集合soe＝{soe1，soe2......soene}，soed＝{soev1,soev2......soevnse}，其中ed与soed一一映射，1≤d≤ne；soevtemp1为svi中svij轮廓中的svijk的别名，1≤temp1≤nse；建立面上采样点集合sof＝{sof1，sof2......sofnf}，sofi＝{sofv1,sofv2......sofvnsf}，其中fi与sofi一一映射，nsf为sofi中采样点数量，sofvtemp2为svi中svij轮廓中的svijk的别名，1≤temp2≤nsf。

以采样点svijk为例，如果svijk与uvfi顶点中的某一顶点的欧式距离小于εv，则将svijk标记为onedge；或者svijk与uvfi边中的某一条边的欧式距离小于εe，则将svijk标记为onedge，并将svijk插入与该边插入soe中的与之对应的集合；如果svijk与uvfi的三条边的欧式距离都大于εe并且与三个顶点的欧式距离都大于εv，并且svijk在uvfi内部，则将svijk标记为insideface，并将svijk插入sofi；如果svijk与uvfi的三条边的欧式距离都大于εe并且与三个顶点的欧式距离都大于εv，并且svijk在uvfi外部，则将svijk标记为outsideface。其中，εv取1.0*10^-3,εe取5.0*10^-4。判断位于内部还是外部的方法如下：

因为需要计算外积，所以先将svijk坐标和顶点坐标拓展到三维，且第三维赋值0.0。svijk坐标变为uvvi1坐标变为uvvi2坐标变为uvvi3坐标变为然后通过(3.4),(3.5),(3.6)计算，

得到如果方向完全相同，则svijk在uvfi内部；如果方向不完全相同，则svijk在uvfi外部。

接着，通过采样点得到采样边集合se＝{se1,se2......senf}，sei＝{sei1,sei2......seisne}。其中，sei与si一一映射，即sei为根据si中采样点位置得到的采样边集合，siq为第q个插入sei的采样边，1≤q≤sne，sne为sei中采样边数量。得到采样边的具体方式如下：

依次以svij1和svij2，svij2和svij3……svijk和svijk+1……svijnse-1和svijnse，以及svijnse和svij1为采样边端点，判断是否需要插入sei中。以svijk和svijk+1为例，并设当前需要的判断的采样边为seexample1，1≤example1≤sne，如果svijk和svijk+1的标记情况符合以下任意一种情况，

①svijk:insidefacesvijk+1:insideface

②svijk:insidefacesvijk+1:onedge

③svijk:onedgesvijk+1:insideface

则将seexample1插入sei；如果svijk和svijk+1的标记情况符合下面两种情况的一种，

①svijk:insidefacesvijk+1:outsideface

②svijk:outsidefacesvijk+1:insideface

则按照下面步骤：

1)分别计算uvfi的三个顶点到seexample1的距离dist1。

2)如果某一顶点与seexample1的欧式距离小于dist1≤εe，进行步骤a，否则，进行步骤b。

a.将seexample1中被标记为outsideface的端点坐标替换为该顶点坐标，然后将seexample1插入sei。

b.判断uvfi的三条边uvei1,uvei2,uvei3与seexample1的相交情况，如果某边与seexample1相交，计算交点，并将seexample1中被标记为outsideface的端点坐标替换为交点坐标，然后将交点作为采样点标记为onedge，并将其插入svi1和与该边在soe中对应的集合，然后将seexample1插入sei。

有些采样点位置相同或者两点之间欧式距离小于εv，所以接着需要删除多余的采样点。依次以面片f1,f2......fnf为单位，进行如下步骤：

1)构建采样点集asi，其中分别为与fi三条边对应的soe中的采样点集合

2)基于分治法，找到asi中的最近点对，如果两点之间欧式距离小于εv，进行如下步骤：

删除其中一个采样点，并将以该采样点为端点的采样边的对应端点坐标替换为另一个采样点的坐标。

3)重复2)直至最近点对两点之间欧式距离大于εv。

接着，依次对面片f1,f2......fnf引入变量ancestor，并将ancestor赋值为面片索引。比如f1的ancestor为1，f2的ancestor为2，以此类推。ancestori表示fi的ancestor。

接着，按照如下步骤进行网格细分：

1)依次遍历soe1,soe2......soecne1，以soer为例，找到soer中与er中点的欧式距离最小的采样点soevdismin。其中，dismin取值唯一且1≤dismin≤nse；cne1为变量，随网格边最大索引值变化而变化，值始终与当前网格边索引最大值相等，初始值为ne；1≤r≤cne1,r∈n+。根据soevdismin的几何信息在网格中生成新的顶点vnewa，其中，newa为生成新顶点后网格顶点最大索引值，vnewa的几何信息包括和其中为vnewa的模型坐标，为vnewa的uv坐标，和计算过程如下：

其中，为er端点模型坐标。为soevm的坐标。scalet1的计算过程如下：

①分别计算的uv坐标u轴和v轴的坐标差值udiff和vdiff，其中

②如果udiff＜＝εthreshold,按照方式a计算；如果vdiff＜＝εthreshold，按照方式b计算；如果udiff＞εthreshold且vdiff＞εthreshold，按照方式c计算

其中，的uv坐标为的uv坐标为对er引入变量splitvertex，将vnewa赋值予splitvertex，splitvertexr表示与er对应的分割点变量。

2)将任意一条边上包含splitvertex变量(splitvertex不为空值)的面片插入集合(元素不重复)wsf1，具体步骤如下：

①依次遍历f1,f2......fcnf1，如果面片的三条边中的任意一条边包含变量splitvertex(splitvertex不为空值)，将该面片插入wsf1，其中cnf1随网格面片最大索引值变化而变化，值始终与当前网格面片索引最大值相等。

②依次遍历wsf1中面片，直至所有面片被遍历。以fexm为例，如果fexm的最长边上不包含变量则参照中点几何信息，在网格上生成新的顶点vnewb，其中，1≤exm≤cnf1,exm∈n+,fexm∈wsf1；longest表示该边为fexm最长边，为fexm的最长边；为的分割点变量；newb为成新顶点后网格顶点最大索引值，vnewb的几何信息包括和其中为vnewb的模型坐标，为vnewb的uv坐标，和计算过程如下：

其中，为两个端点的模型坐标；为两个端点的uv坐标。

③将vnewb赋值予

④以面片fexm为单位，删除与vnewb的uv坐标欧式距离小于εv的采样点，具体步骤如下：

a.构建采样点集asexm，其中分别为与fexm三条边对应的soe中的采样点集合

b.依次遍历asexm中元素，删除与vnewb的uv坐标的欧式距离小于εv的采样点，并将以这些采样点为端点的采样边的对应端点坐标替换为vnewb的uv坐标

⑤如果另一个以为边的三角面片没有在wsf中，则将其插入wsf。

3)依次遍历wsf中元素，根据各面片边上变量splitvertex建立拓扑关系，细分网格，以fexm为例，具体步骤如下：

①如果fexm中有且只有1条边上有变量splitvertex(splitvertex不为空值)，以边上splitvertex和不含splitvertex的两条边的公共顶点为端点，构建新边，将三角面片分割为2个新面片，如图3；如果fexm中有且只有2条边上有变量splitvertex(splitvertex不为空值)，连接两个splitvertex，构成第一条新边；因为连接splitvertex和另外两条边公共顶点有两种情况(如图4(a),图4(b))，所以比较这两种情况下新建边的长度，选取更短的情况构成第二条新边。新建的两条新边将面片分为3个新面片，如图4(b)。如果fexm中有3条边上有变量splitvertex(splitvertex不为空值)，依次连接三个splitvertex，构成三条新边，将三角面片分割为4个新面片，如图5。

②将fexm被分割前与fexm三条边分别一一对应d的中的采样点和sofexm中的采样点分配到与新网格面片一一对应的采样点集合和新网格边一一对应的采样点集合中，并将这些集合分别插入sof和soe。

③将ancestorexm变量值赋予通过分割fexm得到的新面片的ancestor变量。

4)重复1)—3)，直至soe1,soe2......soecne1都变为空集。然后遍历sof1,sof2......sofcnf1，以sofexm2为例，其中，1≤exm2≤cnf1,exm2∈n+。具体步骤如下：

①依次遍历sofexm2中采样点元素，找到与uvfexm2重心的欧式距离最小的采样点sofvdismin，根据sofvdismin几何信息，在网格上生成新的顶点vnewc。其中，newc为生成新顶点后网格顶点最大索引值，vnewc的几何信息包括和其中为的模vnewc型坐标，为vnewc的uv坐标，和计算过程如下：

其中，分别为fexm2三个顶点的模型坐标；

scalem1,scalen1的计算过程如下：

其中，分别为fexm2三个顶点的uv坐标；

②将vnewc与fexm2顶点分别连接，构成三条新边，将面片分割为三个新面片，如图6。

③将与fexm2一一对应的sofexm2中采样点分配到与新网格面片一一对应的采样点集合和新网格边一一对应的采样点集合中，并将这些集合分别插入sof和soe。

④将ancestorexm2变量值赋予新面片的ancestor。

5)重复1)—4)，直至soe1,soe2......soecne1，sof1,sof2......sofcnf1都变为空集。

接着，根据ancestor变量建立af＝{af1,af2......afnf}，afexm3＝{ftemp3|(ancestortemp3＝exm3)∧(1≤temp3≤cnf2∧cnf2∈n+)}，其中，1≤exm3≤nf,exm3∈n+；cnf2随网格面片最大索引值变化而变化，值始终与当前网格面片索引最大值相等。

接着，计算采样边与网格边的相交情况，细分网格。依次遍历af＝{af1,af2......afnf}，以afexm3为例，具体步骤如下：

1)依次遍历afexm3中的面片元素，对于面片的各条边，如果以该边为边的两个面片的ancestor值都与集合对应的ancestor值相同，则将该边插入集合aeexm3，其中aeexm3中元素不重复。

2)依次遍历seexm3中采样边元素，判断与aeexm3中网格边的相交情况，细分网格。以se^exmt为例，其中，se^exmt表示se^exmt∈seexm3。具体步骤如下：

①根据se^exmt端点坐标和aeexm3中网格边顶点uv坐标将se^exmt和aeexm3中网格边元素转至普吕克坐标系(plückercoordinates)。

②建立集合inserteexm3。依次遍历aeexm3中各元素，比如ae^exmt，其中，ae^exmt表示ae^exmt∈aeexm3。在普吕克坐标系下，计算ae^exmt与se^exmt是否相交，如果相交，将ae^exmt插入集合inserteexm3。

③依次遍历inserteexm3中网格边元素，根据交点生成网格顶点，建立wsf2集合(无重复元素)，以ae^exmt为例，具体过程如下：

根据ae^exmt和se^exmt顶点几何信息，在网格上生成新的顶点vnewd。其中，newd为当前网格顶点数量，vnewd的几何信息包括和其中为vnewd的模型坐标，为vnewd的uv坐标，和计算过程如下：

其中，分别为ae^exmt端点ev^exmt1，ev^exmt2的uv坐标；分别为ev^exmt1，ev^exmt2的模型坐标；scalet2的计算过程如下：

将vnewd赋值予ae^exmt的splitvertex变量。将以ae^exmt为边的面片插入wsf。

④依次遍历wsf中面片元素，进行网格细分。细分方式与(1.5)的2)中③相同。

⑤将通过本次细分得到的新的网格边插入aeexm3。

(三)3d浮雕网格重建

根据面片构建对应的纹理面片集合其中，cnf3为变量，随网格面片最大索引值变化而变化，值始终与当前网格面片最大索引值相同。

接着，根据分割纹理，得到纹理集合s2＝{s1,s2......scnf3}，其中，uvfexm5与sexm5一一映射，1≤exm5≤cnf3,cnf3∈n+。

接着，根据纹理图像像素值，判断面片的颜色属性。依次遍历以uvfexm5为例，具体步骤如下：

1)将uvfexm5顶点坐标转至sexm5图像坐标系下，以为例，其中1≤temp5≤3,temp5∈n+，具体步骤如下：

转至sexm5图像坐标系下变为

2)在图像坐标系下，遍历位于sexm5内部的像素点，如果像素值为0的像素点数量占所有位于sexm5内部的像素点数量的εcolor，则将该面片标记为blackface；同理，如果像素值为255的像素点数量占εcolor，则将该面片标记为whiteface。εcolor通常取90％，因误差等因素，可逐渐降低εcolor，直至可以判断面片颜色属性。

接着，标记网格边和顶点的边缘属性。遍历其中，cne3为变量，随网格边最大索引值变化而变化，值始终与当前网格边最大索引值相同。以eexm6为例，其中，1≤exm6≤cne3,exm6∈n+。如果以eexm6为边的两个三角面片的颜色属性不一致，则将eexm6标记为boundaryedge，同时将eexm6的两个端点标记为boundaryvertex。

接着，标记网格顶点的颜色属性。遍历其中，cnv3为变量，随网格顶点最大索引值变化而变化，值始终与当前网格顶点最大索引值相同。以vexm7为例，其中，1≤exm7≤cnv3,exm7∈n+。如果vexm7没有被标记为boundaryvertex，说明vexm7的一阶领域三角面片颜色属性相同，且vexm7与一阶领域三角面片颜色属性相同，比如vexm7的一阶领域三角面片颜色属性为blackface，则将vexm7标记为blackvertex。

接着，标记网格面片边缘属性，依次遍历面片f1,f2......fcnf3，以fexm5为例，具体步骤如下：

1)依次遍历fexm5三个顶点如果三个顶点都没有被标记为boundaryvertex，则将fexm5标记为notboundaryface；如果至少有一个顶点被标记为boundaryvertex，继续执行2)。

2)依次遍历fexm5三条边有以下3种标记情况：

①没有边被标记为boundaryedge，且fexm5颜色属性为blackface，则将fexm5标记为boundaryinface。

②没有边被标记为boundaryedge，且fexm5颜色属性为whiteface，则将fexm5标记为boundaryoutface。

③至少有一边被标记为boundaryedge，则将fexm5标记为boundaryface。

接着，为了避免在下一步中生成非流形网格，需要根据浮雕边缘网格顶点拓扑信息，生成网格点环，具体步骤如下：

1)建立网格边不重复集合ringedge，网格顶点集合ringvertex，依次遍历v＝{v1,v2......vcnv3}，以vexm7为例，如果以vexm7为端点的网格边中，有两条以上(不包含两条)的网格边被标记为boundaryedge，将vexm7插入ringvertex。

2)生成网格顶点。依次遍历ringvertex中网格顶点元素，以ringvertex中v^ring为例，其中，v^ring∈ringvertex。遍历以v^ring为端点的所有网格边，以e^ring为例，其中，e^ring表示以v^ring为端点的网格边。根据e^ring几何信息，生成网格顶点vnewe，其中，newe为生成新顶点后网格顶点最大索引值，vnewe的几何信息包括和其中为vnewe的模型坐标，为vnewe的uv坐标，和计算过程如下：

其中，分别为v^ring模型坐标和uv坐标；分别为e^ring另一个端点的模型坐标和uv坐标；εring取2.0*10^-5。将vnewe赋值予e^ring的splitvertex变量。

3)生成网格拓扑信息。依次遍历ringvertex中网格顶点元素，以v^ring为例，具体步骤如下：

①遍历v^ring的一阶领域三角面片，以f^ring为例，其中，f^ring表示v^ring的一阶领域三角面片。根据网格顶点，建立拓扑信息。为了方便表示，以v^ring为起始顶点，逆时针遍历f^ring顶点，分别赋予临时别名v¹,v²,v³。删除f^ring，构建新三角面片：以v¹,splitvertex¹,splitvertex²为顶点的fnew1；以v²,splitvertex¹,splitvertex²为顶点的fnew2；以v²,v³,splitvertex¹为顶点的fnew3。其中，splitvertex¹是以v¹,v³为端点的网格边对应的splitvertex，splitvertex²是以v¹,v²为端点的网格边对应的splitvertex；new1,new2,new3分别为生成新面片后网格面片最大索引值。如图7。

②标记新面片的颜色属性。将v^ring的一阶领域三角面片标记为whiteface；将vi的二阶领域三角面片标记为原面片颜色属性，如图8。

接着，清除网格顶点，边，面片的边缘属性，迭代进行(三)中这步之前的步骤，直至所有网格顶点都满足：以该顶点为端点的所有网格边中，有不超过2条被标记为boundaryedge。

接着，根据被标记为boundaryvertex生成新的网格顶点。具体步骤如下：

1)建立集合boundarysetvertex。依次遍历网格顶点v＝{v1,v2......vcnv4}，cnv4随网格顶点最大索引值变化而变化，值始终与当前网格顶点最大索引值相同。以vexm8为例，其中，1≤exm8≤cnv4,exm8∈n+。如果vexm8被标记为boundaryvertex，则将vexm8插入boundarysetvertex。

2)生成新的网格顶点。依次遍历boundarysetvertex中顶点元素，以vexm8为例，根据vexm8几何信息，生成新的网格顶点vnewf，其中，newf为生成新顶点后网格顶点最大索引值，vnewf的几何信息包括和其中为vnewf的模型坐标，为vnewf的uv坐标，和计算过程如下：

其中，为vexm8模型坐标；为vexm8的uv坐标；为的归一化法线坐标；εrelief在网格归一化的情况下取0.1就可以得到凸出明显的浮雕。为引入变量above，并将赋值予above。

3)根据网格顶点，建立拓扑信息。具体步骤如下：

①建立浮雕边缘拓扑信息。首先建立boundarysetedge。依次遍历e＝{e1,e2......ecne4}，其中，cne4随网格边最大索引值变化而变化，值始终与当前网格边最大索引值相同。以eexm9为例，其中，1≤exm9≤cne4,exm9∈n+。如果eexm9被标记为boundaryedge，将eexm9插入集合boundarysetedge。然后依次遍历boundarysetedge中网格边元素，以eexm9为例，eexm9有两个端点，为了方便表示，按照如下方式赋予端点别名：

eexm9被标记为boundaryedge，说明以eexm9为边的三角面片颜色属性一个为blackface，一个为whiteface，暂称颜色属性为blackface的三角面片为以中非eexm9端点的顶点为起点，逆时针遍历，先遍历到的顶点称为后遍历到的称为

新建面片fnew4,fnew5，fnew4的顶点为above¹,above²；fnew5的顶点为above²,其中，above¹,above²分别为的above变量值。如图9。

②创建浮雕表面拓扑信息。首先，创建集合reliefface。依次遍历f＝{f1,f2......fcnf4}，其中，cnf4随网格面片最大索引值变化而变化，值始终与当前网格面片最大索引值相同。将被标记为boundaryface和boundaryinface的面片插入reliefface。接着，依次遍历reliefface，以fexmf为例，其中，1≤exmf≤cnf4,exmf∈n+。依次遍历fexmf的顶点以为例，其中，1≤temp3≤3,temp3∈n+。如果不为空值，则用替代成为新的顶点，其中，表示对应的above值。所有顶点更改后构成新面片，删除原面片fexmf。如图10。

接着，建立集合blacksetvertex。依次遍历v＝{v1,v2......vcnv5}，其中，cnv5随网格顶点最大索引值变化而变化，值始终与当前网格顶点最大索引值相同。以vexmv为例，其中，1≤exmv≤cnf5,exmv∈n+。如果vexmv没有被标记为boundaryvertex，且vexmv的颜色属性为blackvertex，则将vexmv插入集合blacksetvertex。

接着，根据顶点几何信息，调整顶点位置。依次遍历blacksetvertex，以v^bs为例，其中，v^bs表示v^bs∈blacksetvertex。v^bs新的模型坐标计算过程如下：

其中，为v^bs未调整前的模型坐标；为v^bs的归一化法线坐标；εrelief在网格归一化的情况下取0.1就可以得到凸出明显的浮雕。

(四)网格重构后模型文件的导出

根据(一)～(三)得到的半边数据结构和网格数据，可以通过assimp等库导出网格重构后的模型文件。