一种基于随机森林改进的实体解析方法

本发明涉及数据处理
技术领域：
，尤其是涉及一种基于随机森林改进的实体解析方法。
背景技术：
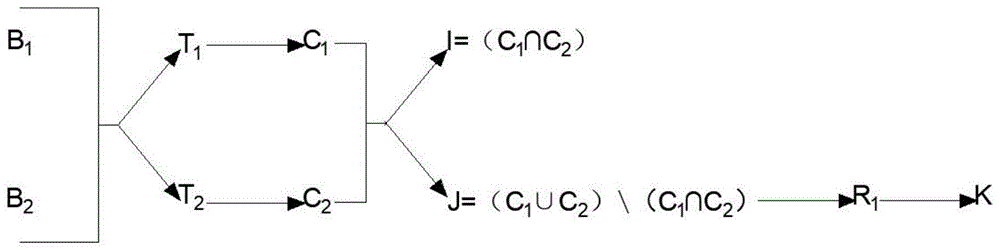
：在数据集中,数据所指向的现实世界中的对象,一般称之为实体。对于同一实体,在不同甚至同一数据集中,可能存在多种不同的表现或描述形式,当将多个不同来源的数据集进行合并以分析处理时,这些对于同一实体的描述则会混杂在一起,造成一定程度的重复现象。实体解析,就是对数据集中的多种不同的描述进行识别、连接，确定哪些描述映射于现实世界中的同一实体的过程。实体解析是数据预处理过程中的一个重要步骤,主要用于解决数据的重复冗余等质量问题。目前的实体解析是指不同的数据对同一个事物即实体可能会有不同的描述(这里的描述包括数据格式、表示方法等)，但它们通常在描述存储的过程中可能会出现排版或者错别字等错误，增加我们数据处理解析的时间并且容易造成匹配的冗余无法精准的得到我们想要的数据集。技术实现要素：本发明的目的在于提供一种基于随机森林改进的实体解析方法，能够通过随机森林对字符串与实体的匹配进行相似度的连接，提高对数据集匹配的准确性和效率，克服现有的实体解析技术的不足。本发明提供的一种基于随机森林改进的实体解析方法，包括以下步骤：s1：提供一个包括k个决策树的随机森林f，其中k＝1,2，，，n；提供若干个字符串bi，其中i＝1,2，，，n；s2：执行修剪步骤，所述修剪步骤包括：s2.1：从所述k个决策树中提取m个决策树t1，t2，，，tm，分别使用所述t1，t2，，，tm执行每一个所述字符串bi，得到输出c1，c2，，，cm；s2.2：建立集合i＝c1∩c2∩，，，∩cm；s3：执行验证步骤，所述验证步骤包括：s3.1：建立集合j＝(c1∪c2∪，，，∪cm)\(c1∩c2∩，，，∩cm)；s3.2：从所述随机森林f中提取n个决策树r1，r2，，，rn，使用所述r1，r2，，，rn执行所述集合j，以生成集合k1，k2，，，kn，且其中s4：所述随机森林f输出实体解析结果为i∪k1∪k2∪，，，∪kn。进一步地，s1包括以下训练步骤：s1.1：给定若干个样本数据表ai，其中i＝1,2，，，n；s1.2：从ap表中随机选择一组xp元组，从aq表中随机选择与所述ap表可能匹配的一组xq元组，将所述xp与所述xq配对组成样本s，其中：p∈i，q∈i，p≠q；s1.3：检查所述ap表与所述aq表的模式，创建一组特性，使用所述特性将所述样本s中的元组对转换为特征向量；s1.4：使用s1.3中的所述特征向量训练所述随机森林f。进一步地，s3.2中，(r1，r2，，，rn)∪(t1，t2，，，tm)＝随机森林f。进一步地，s2.1中，所述m为正确解析所需要的最小的决策树数量，所述正确解析为所述随机森林f将所述字符串bi正确解析为实体。进一步地，s1.2中，在所述aq表中构建反向索引，使用所述反向索引快速查找所述aq表中与所述xp元组共享x个符号的元组，组成xq元组，其中x≥2。进一步地，s2中，在执行前对所述k个决策树进行修剪。本发明通过减少需要匹配的候选对的数量，缩小样本，然后通过缩小的样本训练随机森林，以缩短时间，通过将执行每一个决策树分解为在修剪步骤中执行树的子集，然后在验证步骤中执行剩余的树，通过树的重用计算简化执行决策树集，以再次缩短时间，精简数据、精确解析结果。附图说明为了更清楚地说明本发明具体实施方式或现有技术中的技术方案，下面将对具体实施方式或现有技术描述中所需要使用的附图作简单地介绍，显而易见地，下面描述中的附图是本发明的一些实施方式，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据这些附图获得其他的附图。图1为本发明的实体解析流程示意图；图2为传统的实体解析流程示意图；具体实施方式应该指出，以下详细说明都是例示性的，旨在对本申请提供进一步的说明。除非另有指明，本文使用的所有技术和科学术语具有与本申请所属
技术领域：
的普通技术人员通常理解的相同含义。需要注意的是，这里所使用的术语仅是为了描述具体实施方式，而非意图限制根据本申请的示例性实施方式。如在这里所使用的，除非上下文另外明确指出，否则单数形式也包括复数形式，此外，还应当理解的是，当在本说明中使用术语“包含”和/或“包括”时，其指明存在特征、步骤、操作、器件、组件和/或它们的组合。下面将结合实施例对本发明的技术方案进行清楚、完整地描述，显然，所描述的实施例是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。实施例1：本发明提供的一种基于随机森林改进的实体解析方法，包括以下步骤：s1：提供一个包括k个决策树的随机森林f，其中k＝1,2，，，n；提供若干个字符串bi，其中i＝1,2，，，n；对随机森林f执行训练步骤；s1.1：给定若干个样本数据表ai，其中i＝1,2，，，n；s1.2：从ap表中随机选择一组xp元组，从aq表中随机选择与ap表可能匹配的一组xq元组，将xp与xq配对组成样本s，其中：p∈i，q∈i，p≠q；s1.2中，在aq表中构建反向索引，使用反向索引快速查找aq表中与xp元组共享x个符号的元组，组成xq元组，其中x≥2。s1.3：检查ap表与aq表的模式，创建一组特性，使用特性将样本s中的元组对转换为特征向量；s1.4：使用s1.3中的特征向量训练随机森林f。例如，s1.1中，给定两个样本数据表a1和a2，s1.2中，从a1表中随机选择一组x1元组，从a2表中随机选择与a1表中可能匹配的一组x2元组，将x1与x2配对组成样本s。s1.3中，通过检查a1表和a2表的模式，创建一组特性，创建该特性的方法，例如，如果检测到属性city属于string类型，则就会创建许多使用字符串相似性度量的特性，举例：editdist(a1.city,a2.city)，jaccard2gram(a1.city,a2.city)。s2：执行修剪步骤，修剪步骤包括：s2.1：从k个决策树中提取m个决策树t1，t2，，，tm，分别使用t1，t2，，，tm执行每一个字符串bi，得到输出c1，c2，，，cm；s2.2：建立集合i＝c1∩c2∩，，，∩cm；s3：执行验证步骤，验证步骤包括：s3.1：建立集合j＝(c1∪c2∪，，，∪cm)\(c1∩c2∩，，，∩cm)；s3.2：从随机森林f中提取n个决策树r1，r2，，，rn，使用r1，r2，，，rn执行集合j，以生成集合k1，k2，，，kn，且其中s4：随机森林f输出实体解析结果为i∪k1∪k2∪，，，∪kn。如图1所示：例如，s1中，随机森林f包括3个决策树，分别为t1、t2和r1，s2中，提供两个字符串b1和b2，在b1和b2上执行t1、t2，得到输出c1和c2，则s3中，建立集合i＝c1∩c2，则i是由t1和t2预测匹配的所有对组成，可以作为随机森林f输出的一部分，则s4中，建立集合j＝(c1∪c2)\(c1∩c2)，则s5中，使用r1执行集合j，以生产集合k，所以显然k也匹配随机森林f，所以随机森林f的输出是i∪k，任何其他对(既不在i中也不在j中)都不能被t1和t2预测匹配，因此不能与随机森林f匹配。另外，s2中，集合j往往比较小，因此，将树t3应用于j中往往比将其应用于原始的字符串b1和b2集合要快得多。当f很大时，比如10棵树，节省的时间非常可观。假设在这种情况下，我们需要至少5棵树来匹配f，然后我们可以在b1和b2上应用6棵树来得到集合i和j，然后将剩下的4棵树应用到相对较小的集合j上，前者即树的修剪，后者即树的验证。具体为：考虑一个由10棵树组成的森林f，其中至少有5棵树必须匹配才能使f匹配。然后修剪步骤执行6棵树来产生一组对j，在修剪过程中考虑一对p1∈j与4棵树匹配。然后，只要剩下的4棵树中的一棵与p1匹配，我们就可以将p1声明为匹配；考虑一对p2∈j在剪枝时只与一棵树匹配，当剩下的4棵树中的一棵预测p2不匹配时，我们就可以宣布p2不匹配。所以，在s2中，m个决策树t1，t2，，，tm执行过程即修剪过程；s5中，r1，r2，，，rm的执行过程即验证过程，验证过程可以简化数据处理解析的时间。s3.2中，s3.2中，(r1，r2，，，rn)∪(t1，t2，，，tm)＝随机森林f。充分利用随机森林f中的所有树，使解析结果更准确。s2.1中，所述m为正确解析所需要的最小的决策树数量，所述正确解析为所述随机森林f将所述字符串bi正确解析为实体。当修剪步骤使用能够保证正确解析的最少的决策树数量m，则验证步骤使用剩余的决策树数量n，此时明显的，对于缩短解析时间的效果是最大的，因为修剪步骤需要执行所有的字符串，而验证步骤只需要执行修剪后的集合j。s2中，在执行前对k个决策树进行修剪。应用树的子集进行修剪，修剪作用是为了避免过拟合，之后用剩余的树应用j进行验证。实施例2：本实施例中，考虑匹配两组名称，这两组名称同时包含长名(例如graphenenanospheres)和短名(例如golfball)。通过执行随机森林f的修剪和验证对两组字符串b1和b2进行匹配获取想要的字符串。matches(b11,b21)(b12,b21)(b13,b22)为了匹配两组字符串b1和b2，我们学习随机森林f，然后在b1和b2上执行f。本发明执行过程在于，我们将f的执行分为两个步骤：修剪和验证。以下描述如何有效地执行这两个步骤。假设随机森林f有k棵树，其中至少需要dk/2e树以便f匹配。那么显而易见，剪枝步骤至少执行(bk/2c+1)个树时，任何不由该步骤输出的字符串对都不能是匹配的。如图2所示，假设随机森林f只在三棵树中至少有两棵树输出同一对时，才输出一对(即声明它是匹配的)。简单地说，我们可以在两组字符串b1和b2上执行f，方法是执行b1和b2上的每个树ti以获得输出ci，然后输出出现在至少两个树的输出中的所有对(参见图2)，这是比较耗时的一种方法。如图1所示，本发明的优点是只执行两个树，比如在b1和b2上执行t1、t2，以获得输出c1和c2(参见图1)。集合i＝c1∩c2由t1、t2预测匹配的所有对组成，因此可以作为随机林f输出的一部分立即输出。修剪步骤的实施过程为：集合j＝(c1∪c2)\(c1∩c2)，由仅由一棵树(t1或t2)预测匹配的所有对组成。很容易看出，我们只需要将剩下的树r1应用于集合j，设k是j中r1预测匹配的对的集合，显然任何这样的对也是随机森林f的匹配，因为它正好由两棵树(t1或t2，以及r1)匹配。因此，随机林f的输出为i∪k(见图1)。任何其他配对(即i和j中的配对)都不能由t1和t2预测匹配，因此不能与f匹配。验证步骤的实施过程为：集合j往往相对较小，因此，将树r1应用于j往往比将其应用于字符串b1和b2的原始集合快得多，当f较大时(例如10棵树)，这种时间节省是非常显著的；假设在这种情况下，我们至少需要五棵树来匹配f。然后我们可以将六棵树应用于b1和b2以获得集合i和j(即修剪步骤)，然后将其余四棵树应用于相对较小的集合j(即验证步骤)。在验证步骤中，假设在之前的剪枝步骤中执行修剪tm树产生一组对j，则需要考虑如何对j执行剩余的树：使u为在集合j上执行的剩余的树的集合，类似于在修剪步骤中执行树的方式，这里可以简单地使用上面的优化过程来生成一个计划p，该计划p以组合方式执行u中的所有树(即重用计算)，但是更好的解决方案是按顺序应用树，以避免将u中的所有树应用于j中的所有对。综上，本发明通过训练包含k个决策树的随机森林，输入引用集合内的字符串，执行随机森林中的决策树构建新的集合i，j，利用集合i，j构建随机森林的输出，完成引用集合与现实实体的匹配，并且在对随机森林的执行过程中，可以利用构造的集合j对匹配进行验证。最后应说明的是：以上各实施例仅用以说明本发明的技术方案，而非对其限制；尽管参照前述各实施例对本发明进行了详细的说明，本领域的普通技术人员应当理解：其依然可以对前述各实施例所记载的技术方案进行修改，或者对其中部分或者全部技术特征进行等同替换；而这些修改或者替换，并不使相应技术方案的本质脱离本发明各实施例技术方案的范围。当前第1页12