针对排序系统鲁棒性的评估方法及系统

1.本发明涉及信息技术领域，特别涉及一种针对排序系统鲁棒性的评估方法及系统。


背景技术：

2.近年来，排序系统在选举投票、体育竞赛、广告推荐等应用中都发挥着重要作用，因而排序系统具有重大的经济价值和社会影响力。一旦攻击者破坏排序系统的排序聚合算法的生成结果，势必会造成巨大的破坏。
3.排序系统的鲁棒性作为机器学习领域的重要研究方向，近年来受到了广泛关注。分析排序系统的鲁棒性，首先需要设计相应的攻击方法对排序系统进行攻击测试，进而发现排序系统中潜在的漏洞或者风险，从而实现对排序系统鲁棒性的评估。然而，目前针对排序系统的鲁棒性，还未有成熟的评估方法。
4.因此，针对排序系统的鲁棒性进行评估实为亟待解决的问题。


技术实现要素：

5.为了解决上述问题，本发明的主要目的在于提供一种针对排序系统鲁棒性的评估方法及系统，能够针对排序系统的排序聚合算法在应用中面临的安全风险，具体包括面向排序聚合算法的投毒攻击机制和相应的快速求解算法，从攻击者所具有的知识和能力两个维度对可能的攻击场景进行划分，设计不同的攻击机制，进而评估排序系统的鲁棒性。
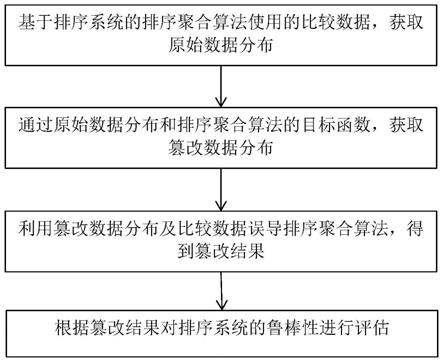
6.为了实现上述目的，本发明提供了一种针对排序系统鲁棒性的评估方法，包括：基于排序系统的排序聚合算法使用的比较数据，获取原始数据分布；通过所述原始数据分布和所述排序聚合算法的目标函数，获取篡改数据分布；利用所述篡改数据分布及所述比较数据误导所述排序聚合算法，得到篡改结果；根据所述篡改结果对所述排序系统的鲁棒性进行评估。
7.为了实现上述目的，本发明还提供了一种针对排序系统鲁棒性的评估系统，包括：原始数据获取模块，用于基于排序系统的排序聚合算法使用的比较数据，获取原始数据分布；篡改数据获取模块、用于通过所述原始数据分布，获取篡改数据分布；篡改结果转化模块、用于利用所述篡改数据分布及所述比较数据误导所述排序聚合算法，得到篡改结果；鲁棒性评估模块，用于根据所述篡改结果对所述排序系统的鲁棒性进行评估。
8.由以上方案可知，本发明的优点在于：在本发明提出针对比较数据的高效投毒方式，并在此基础上，建立了基于动态博弈和静态博弈的投毒机制，分别模拟攻击者具有完全知识条件和有限知识条件下的攻击行为，为后续评估排序系统的鲁棒性提供可靠工具。
附图说明
9.图1为本发明一实施例的针对排序系统鲁棒性的评估方法的流程图。
具体实施方式
10.为让本发明的上述特征和效果能阐述的更明确易懂，下文特举实施例，并配合说明书附图作详细说明如下。
11.在本发明的一个实施例中，提供一种针对排序系统鲁棒性的评估方法，能够使得待评估的排序系统产生特定的排序结果，并根据该特定的排序结果对排序系统进行评估。其中，主要过程说明如下：
12.第一，当给定了排序系统的排序对象的集合v＝[n]，其中n为排序对象的数目。排序系统的排序聚合算法所使用的比较数据是集合v中若干元素的有序排列，具体地，所述若干元素的有序排列的最简单的形式可为一对排序对象所组成的成对比较(pairwise comparison),所述成对比较可记为(i，j)∈v
×
v，i≠j，其表示在n个排序对象组成的有序排列之中，排序对象i排在排序对象j之前。多个排序对象组成的比较数据均可以转化为成对比较的形式。攻击者对比较数据的篡改，可以归纳为在原始数据集d
original
＝{(i，j)|i，j∈v，i≠j}中：(1)增加，即增加一个成对比较(2)修改，即将成对比较(i，j)∈d
original
改变为成对比较(j，i)；(3)删除，即将成对比较(i，j)∈d
original
移出原始数据集d
original
。统计所有可能的成对比较在原始数据集d
original
中所出现的次数，并记为其中n＝n(n
‑
1)。此时，对原始数据集d
original
进行的增加、修改和删除操作则全部变为对各类的成对比较出现次数w0的改变。进一步地，将各类的成对比较在原始数据集d
original
中出现的次数w0进行实数化和归一化处理，从而得到关于原始数据分布p，如下所示：
[0013][0014]
因此，针对排序系统的排序聚合算法的投毒攻击实际上就是，攻击者通过篡改原始数据集d
original
的原始数据分布p，得到篡改数据分布q并且利用篡改数据分布q误导排序系统的排序聚合算法生成排序结果的攻击行为。
[0015]
第二，完全知识条件下的攻击模式。
[0016]
当攻击者掌握排序聚合算法所使用的完整比较数据，排序聚合算法本身的知识(目标函数的种类及其参数)以及排序聚合算法对比较数据的反馈信息(任意数据通过算法聚合时产生的损失)时，可认为攻击者具有对目标排序系统的排序聚合算法的完全知识。在这种情况下，对目标排序系统进行投毒攻击的攻击者基于排序聚合算法的反馈信息来影响比较数据，进而误导排序聚合算法生成排序结果并达到攻击目的。由于排序聚合算法所使用的数据是完整或部分待排序对象的排序，且在排序融合问题中，往往不涉及待排序对象的特征，因此攻击者对原始数据集所能进行的操作仅有增加(即在原始数据集中加入待排序对象间特定的排序关系)，修改(即改变原始数据集中的待排序对象间的排序关系)和删除(即删除原始数据集已经存在的待排序对象间的排序关系)三种。在面向排序系统的排序聚合算法的投毒攻击中，攻击者的目标是利用篡改篡改分布q来误导排序聚合算法，即找到原始数据分布p周围的篡改数据分布q，使得排序聚合算法以篡改数据分布q作为输入获得的篡改排序参数θ
q
与以原始数据分布p为输入获得的原始排序参数相差之间的差异达到最
大。具体来说，攻击者的目标对应于以下的问题:
[0017][0018][0019]
其中，表示以p为球心，ρ为半径的球，为表征分布相似性的度量。
[0020]
上述优化问题实际上是由攻击者和排序系统的排序聚合算法二者构成的动态博弈(dynamic game):因为攻击者具有完全知识，掌握了原始数据分布p和排序聚合算法的目标函数l，所以攻击者可以模拟排序聚合算法的执行过程，通过求解下层优化问题(lower
‑
level optimization)
[0021][0022]
来获得原始数据分布p所对应的原始排序参数θ
p
；获得排序聚合算法对原始数据分布p的反馈信息(即上述的原始排序参数)后，攻击者通过求解上层优化问题(upper
‑
level optimization)，获得满足其有限能力约束的篡改数据分布q，即
[0023][0024]
当攻击者获得篡改数据分布q后，可以用较为简单的操作将比较数据的分布转化为成对比较的数据，进而恢复成为任意形式的有序数据并生成投毒攻击可以使用的形式，达到破坏排序聚合算法生成的原始排序结果的目的。由于攻击者具有完全知识，可以准确得到原始排序参数θ
p
，使得攻击者和排序聚合算法进行决策的时间具有明显的先后顺序，攻击者可以根据排序聚合算法的输出来调整自己的行动，因而可以最大限度的暴露排序聚合算法中存在的鲁棒性。
[0025]
事实上，在完全知识条件下，面向排序系统的排序聚合算法的投毒攻击是一个具有层次结构的双层优化问题(bilevel optimization)。一般来说，通常双层优化问题是强np
‑
难(strongly np
‑
hard)问题，对该类优化问题的求解通常较为困难。本发明通过选择特定的排序聚合损失函数l和度量分布相似度的函数确保对应的上层优化问题是一个目标函数为凹函数的最大化问题，同时保证下层优化问题是一个目标函数为凸函数的最小化问题，使得双层优化问题转化成为涉及最大
‑
最小(min
‑
max)的凸优化问题，进而得到面向动态投毒攻击的快速求解算法，从而保证攻击者在完全知识条件下可以进行高效的投毒攻击。
[0026]
在本发明的一个实施实例中，选择加权最小二乘法作为排序聚合算法的目标函数，即
[0027][0028]
其中，矩阵a＝{
‑
1，0，1}
n
×
n
为比较矩阵或设计矩阵，y表示所有可能成对比较的方向，如果存在成对比较(i，j)，那么y
ij
＝1。统计涉及排序对象的集合v的所有可能成对比较，那么y将具有如下的形式
[0029][0030]
在本发明的一个实施实例中，选择φ散度(φ
‑
divergence)中的卡方散度作为分布相似性的度量。令是满足φ(1)＝0的凸函数。那么分布p和q之间的φ散度定义为
[0031][0032]
其中，μ是西格玛有限测度(σ
‑
infinite measure)，满足p，q＜＜μ,且q＝dq/dμ,p＝dp/dμ。当φ是如下的平方函数时，φ散度又被称为卡方散度：
[0033][0034]
当用卡方散度来度量分布相似度时，可以将转化为如下形式：
[0035][0036]
进而，上层优化问题将具有如下形式：
[0037][0038][0039]
其中，z＝l(θ
p
，p)，<p，1>＝∑
(i，j)
p
ij
。
[0040]
第三，有限知识条件下的攻击模式。
[0041]
所谓掌握有限知识的攻击者是指攻击者仅掌握针对排序系统的排序聚合算法的部分知识，即排序聚合算法所使用的完整的原始数据集、排序聚合算法本身的知识以及排序聚合算法对原始数据集的反馈信息三类知识中的一项或者两项。其中，排序聚合算法对原始数据集的反馈信息是较难获得的。获得排序聚合算法对原始数据集的反馈信息需要攻击者获得排序聚合算法某种形式的所有权，但攻击者往往与排序聚合算法分属于不同组织且存在物理隔离，所以在实际问题当中，为进行投毒攻击，攻击者往往只能利用排序聚合算法所使用的完整比较数据和排序聚合算法本身的知识来模拟生成反馈信息。但通过模拟得到的反馈信息可能与排序聚合算法产生的真实反馈信息可能存在极大的差距，导致攻击者对排序聚合算法的攻击失效。针对上述问题，本发明拟引入有限知识的攻击者对排序聚合算法进行攻击，探索攻击者不需要排序聚合算法对比较数据的反馈信息时进行投毒攻击的机制。
[0042]
由于攻击者缺乏排序聚合算法对比较数据的反馈信息，那么攻击者的攻击行为将无法建模成为一个层次化的双层优化问题。于此同时，考虑到有限知识攻击者与完全知识攻击者具有一致的目标，利用篡改数据分布q来误导排序聚合算法，即找到原始数据分布p周围的篡改数据分布q，使得排序聚合算法以篡改数据分布q作为输入获得的篡改排序参数θ
q
与以原始数据分布p为输入获得的原始排序参数θ
p
相差之间的差异达到最大。具体来说，有限知识攻击者的攻击行为对应于以下的问题:
[0043][0044][0045]
该优化问题实际上是由攻击者和排序系统的排序聚合算法二者构成的静态博弈(static game):攻击者仅掌握有限知识，只能同时对篡改数据分布q和模拟排序参数θ进行求解，即找到原始数据分布p周围的篡改数据分布q，而篡改数据分布q是集合中所有可能作为输入的分布中使得目标函数值最大的分布。在上述的静态博弈中，由于篡改数据分布q具有最大化目标函数l的性质，因此篡改数据分布q也称为最差情形分布(worst
‑
case distribution)。与完全知识条件下导出的动态博弈不同，静态博弈中的攻击者与排序聚合算法必须同时做出行动，没有先后次序。在实际应用中，即攻击者仅有一次篡改原始数据集的机会，且无法根据排序聚合算法的输出调整自己的行动策略。这样的设定更符合实际应用中的对抗场景，进而更好地揭示排序聚合算法自身的鲁棒性。
[0046]
在本发明的一个实施例中，加权最小二乘法作为排序聚合算法的目标函数；选择沃瑟斯坦距离(wasserstein distance)作为分布相似度的度量函数：给定a∈[1，∞)，则对两个定义在相同事件集合ω上的分布p，q∈p(ω)，二者之间的a阶沃瑟斯坦散度定义为
[0047]
1≤a＜∞
[0048][0049]
a＝∞
[0050][0051]
其中，γ(p，q)表示所有定义在ω
×
ω的波莱尔概率分布(borel probability distributions)，且边际分布(marginal distribution)为p和q；函数distribution)为p和q；函数为非负函数；γ
‑
ess sup表示测度γ意义下函数d的本质上确界(essential supremum)。
[0052]
在本实施实例中，最终的篡改数据分布q可通过如下步骤进行求解：
[0053]
首先，通过求解如下问题得到最差情形下的模拟排序参数
[0054][0055]
其中，a
(i，j)
是比较矩阵a对应成对比较(i，j)的行向量。
[0056]
其次，通过获得如下变量的值
[0057]
[0058]
再次，通过求解如下的优化问题得到篡改数据分布
[0059][0060]
第四，篡改数据分布转化和鲁棒性评估。
[0061]
根据第二或者第三得到的篡改数据分布，并利用原始数据集中成对比较的数目，将篡改数据分布转化为对应各类成对比较的整数形式并交于待攻击算法进行攻击，从而得到篡改结果；其中待攻击算法可为上述的排序系统的排序聚合算法。最后，根据得到的篡改结果可对排序系统的鲁棒性进行评估。
[0062]
本发明的技术方案通过软件或者硬件的方式均可实现：
[0063]
在本发明的一个实施例中，提供一种针对排序系统鲁棒性的评估系统，包括：原始数据获取模块，用于基于排序系统的排序聚合算法使用的比较数据，获取原始数据分布；篡改数据获取模块、用于通过所述原始数据分布，获取篡改数据分布；篡改结果转化模块、用于利用所述篡改数据分布及所述比较数据误导所述排序聚合算法，得到篡改结果；鲁棒性评估模块，用于根据所述篡改结果对所述排序系统的鲁棒性进行评估。
[0064]
当然，本发明还可有其它多种实施例，在不背离本发明精神及其实质的情况下，熟悉本领域的技术人员当可根据本发明作出各种相应的改变和变形，但这些相应的改变和变形都应属于本发明所附的权利要求的保护范围。