耦合地表土壤含水量的区域尺度最大气孔导度的计算方法与流程

本发明涉及水资源遥感监测和生态水文技术领域，特别涉及一种耦合地表土壤含水量的区域尺度最大气孔导度的计算方法。

背景技术：

地表蒸散发是水循环过程的重要组成部分，获取大时空尺度的蒸散发数据对实现水资源精细化管理有重要意义。pml(penman-monteith-leuning)模型是基于遥感数据进行蒸散发反演的主流方法之一，该模型在penman-monteith模型的基础上引入地表导度，通过建立地表导度与lai(leafareaindex)的关系，实现对地表蒸散发的反演。leuning等人(leuningetal，2008)的研究表明，土壤蒸发系数(f)和最大气孔导度(gsx)是pml模型中最敏感的两个参数。gsx主要通过改变冠层导度来影响植被蒸腾，进而影响到地表总蒸散发的模拟精度。传统的pml模型主要应用于站点尺度的蒸散发模拟，通过优化算法来率定f和gsx，实现对蒸散发的准确模拟(李红霞，2011)，但这种方法难以在区域尺度上推广。因此，建立区域尺度上的gsx参数化方案，对提高pml模型在区域尺度上的适用性有重要意义。

为实现pml模型在区域尺度上的应用，学者们先后提出了多种区域尺度上gsx的参数化方案。zhang等(zhangetal，2017)在利用pml模型进行蒸散发计算时，根据地物类型对gsx赋常值来实现区域尺度的蒸散发模拟；yebra(yebraetal，2013)和易永红(2008)通过建立冠层导度与植被指数的回归关系来对区域尺度的gsx进行计算；zhang等(zhangetal，2010)引入budyko曲线来估计年均蒸发速率，并通过参数率定的方式来得到每个网格的gsx。上述方法均实现了区域尺度的gsx参数化，但总体上是通过回归拟合、参数率定或赋常数等方式得到，对gsx参数化的机理性相对较弱。

在植被散发过程中，气孔是控制植被散发的关键，gsx的变化在很大程度上受到土壤含水量的影响(莫兴国，1997)。而已有的区域尺度gsx参数化方案，对gsx对土壤含水量的响应考虑不足。因此，从土壤水分胁迫对气孔阻力存在的显著影响出发，需要构建物理机理明确的区域尺度gsx计算方法，进一步提高pml模型的科学性和模拟结果的准确性。当前，基于土壤含水量实测数据和神经网络等方法，可生产时空连续的地表土壤含水量产品(段浩，2021)，但基于遥感监测并实现与土壤含水量动态耦合的gsx参数化技术尚未解决。

参考文献

leuningr，zhangyq，rajauda，etal.asimplesurfaceconductancemodeltoestimateregionalevaporationusingmodisleafareaindexandthepenman-monteithequation[j].waterresourcesresearch，2008，44，w10419，doi：10.1029/2007wr006562.

李红霞，张永强，张新华，等.遥感penman-monteith模型对区域蒸散发的估算[j].武汉大学学报(工学版)，2011,44(4)：457-461.

zhangyq，chiewfhs，pena-arancibiaj，etal.globalvariationoftranspirationandsoilevaporationandtheroleoftheirmajorclimatedrivers[j].journalofgeophysicalresearch：atmospheres，2017，122，6868-6881.

yebram，dijkav，leuningr，eta1.evaluationofopticalremotesensingtoestimateactualevapotranspirationandcanopyconductance[j].remotesensingofenvironment，2013，129，250-261.

易永红.植被参数与蒸发的遥感反演方法及区域干旱评估应用研究[d].清华大学，2008.

zhangyq,leuningr,huttleylb,etal.usinglong-termwaterbalancestoparameterizesurfaceconductancesandcalculateevaporation0.05°spatialresolution[j].waterresourcesresearch,2010,46,w05512.

莫兴国.冠层表面阻力与环境因子关系模型及其在蒸散估算中的应用[j].地理研究，1997,16(2)：81-88.

段浩，朱彦儒，赵红莉，等.考虑人类活动用水的土壤含水量神经网络反演研究[j].水利水电科技进展，2021，41(1)：1-6.

技术实现要素：

本发明针对计算区域尺度蒸散发过程中最大气孔导度估算的技术瓶颈，提供了一种耦合地表土壤含水量的区域尺度最大气孔导度的计算方法，解决了基于遥感监测技术，获取蒸散发计算过程中区域尺度最大气孔导度参数的计算问题。

为了实现以上发明目的，本发明采取的技术方案如下：

一种耦合地表土壤含水量的区域尺度最大气孔导度的计算方法，包括以下步骤：

步骤1、筛选地表土壤含水量的影响因子，获取区域尺度上各影响因子的栅格数据；

步骤2、基于地表土壤墒情监测数据，构建基于土壤含水量各影响因子的地表土壤含水量神经网络模拟模型，模拟得到时空连续的地表土壤含水量产品；

步骤3、基于冠层阻力参数化模型，耦合土壤含水量数据，解析冠层最小气孔阻力与冠层阻力的关系，并基于一般形式penman-monteith公式解析地表阻力，构建冠层气孔阻力与地表阻力的关联；

步骤4、基于地表阻力的计算，得到冠层阻力和冠层最小气孔阻力，并利用气孔阻力与气孔导度的反比关系，得到区域尺度的最大气孔导度。

进一步地，所述步骤1包括以下子步骤：

步骤11、根据地表土壤含水量的演变规律，筛选与土壤含水量变化密切相关的影响因子，影响因子包括：降雨、潜在蒸散发、改进型垂直干旱指数(mpdi)、归一化植被指数(ndvi)和地表高程(dem)；

步骤12、采集降雨、ndvi、dem的监测数据或产品，采集气象数据并计算潜在蒸散发，气象数据包括：气温和风速，采集遥感影像数据并计算mpdi指数产品，将上述影响因子统一到相同的空间参考，其中潜在蒸散发和mpdi指数的计算公式分别如式(1)和式(2)所示：

其中，ep为潜在蒸散发，u2是2m处的风速，δ是气压曲线斜率，γ是湿度常数，rn是净辐射，g是土壤热通量，t是2m高度处的气温，esat-ea是饱和水汽压差。

其中，rv，red和rv，nir分别是红光和近红外波段的植被反射率；fv是植被盖度；m是土壤线斜率；rred是大气校正后的红光波段反射率；rnir是大气校正后的近红外波段反射率。

步骤13、将各项影响因子的监测数据插值成栅格格式。

进一步地，所述步骤2包括以下子步骤：

步骤21、采集地表土壤墒情站点的土壤含水量监测数据；

步骤22、从各项影响因子的栅格数据中提取与土壤含水量监测日期对应的站点影响因子数据值；

步骤23、以站点位置的影响因子数据为输入，以相应位置的土壤含水量监测数据为输出，构建基于影响因子的土壤含水量神经网络模拟模型；

步骤24、基于步骤23建立的土壤含水量神经网络模拟模型，模拟得到研究区时空连续的地表土壤含水量产品。

进一步地，所述步骤3包括以下子步骤：

步骤31、；基于冠层阻力参数化模型，耦合土壤含水量数据，冠层阻力参数化模型的公式为：

其中，各分项分别为：

f3＝1-g(esat-ea)式(7)

f4＝(1-1.6*10^-3(298-ta)²)⁴式(8)

其中rcmin为冠层最小气孔阻力；k↓是到达冠层顶部的太阳短波辐射(w/m²)；lai是冠层的叶面积指数；k↓dbl和g分别为冠层最大气孔阻力、辐射临界值和植被系数，为常数；θ为土壤含水量，此处选用基于神经网络模拟得到的区域土壤含水量；θcap、θwilt分别为田间持水量和凋萎含水量，与土壤质地有关；

步骤32、；解析冠层与rc的关系，由冠层阻力参数化模型得到两者的关系为：

步骤33、基于一般形式penman-monteith公式解析地表阻力，rs的计算公式为：

其中，ra为空气动力学阻力，λ为汽化潜热，ρ为空气密度，cp为空气定压比热；

步骤34、根据benmehrez提出的方法，构建冠层阻力rc与rs的关系，计算公式为：

进一步地，所述步骤4包括以下子步骤：

步骤41、根据式(10)计算rs；

步骤42、将步骤41结果带入式(11)，得到rc；

步骤43、根据式(9)计算再根据其与气孔导度的反比关系，得到区域尺度的最大气孔导度。

与现有技术相比，本发明的优点在于：

从气孔导度的机理出发，提出了耦合地表土壤含水量的区域尺度gsx遥感反演方法，该方法具有机理性强、便于实现较大时空尺度计算等优点，有助于进一步提高pml模型对蒸散发模拟的科学性。

附图说明

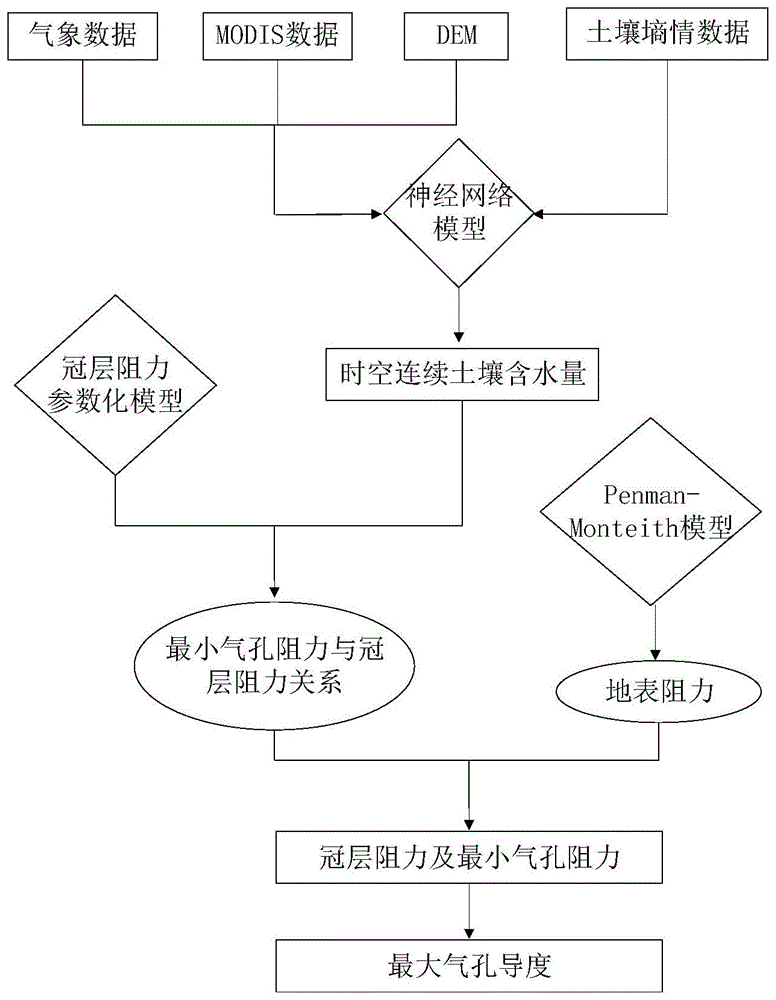
图1为本发明实施例耦合地表土壤含水量计算区域尺度最大气孔导度的流程示意图；

图2为本发明实施例土壤含水量神经网络模拟模型结构示意图；

图3为本发明实施例河北省土壤墒情监测土壤含水量与基于神经网络模型的模拟值对比；

图4为本发明实施例计算得到的2018年3月3日石津灌区1km分辨率地表阻力示例图；

图5为本发明实施例计算得到的2018年3月3日石津灌区1km分辨率最大气孔导度示例图。

具体实施方式

为使本发明的目的、技术方案及优点更加清洗，以下根据附图列举实施例，对本发明做进一步详细的说明。

如图1所示，步骤a、根据研究区位置，采集与土壤含水量变化相关各影响要素数据，并将各影响要素转换为1km空间分辨率的逐日数据；

以河北省土壤墒情观测数据为基础进行全省地表土壤含水量反演，选定的土壤含水量变化影响因子包括降雨、潜在蒸散发(ep)、改进型垂直干旱指数(mpdi)、归一化植被指数(ndvi)和地表高程(dem)；

采集2018年河北省的降雨站点观测数据，并利用arcgis插值工具转为栅格数据；采集dem数据、modis的ndvi数据，并利用河北省矢量文件进行剪裁；

采集2018年河北省的气温、风速、气压、日照时数、相对湿度、最高气温、最低气温等要素的气象站点观测数据，并将站点数据插值为栅格文件，然后利用fao-56公式计算潜在蒸散发，计算方法为：

其中，ep为潜在蒸散发，u2是2m处的风速，δ是气压曲线斜率，γ是湿度常数，rn是净辐射，g是土壤热通量，t是2m高度处的气温，esat-ea是饱和水汽压差。

利用modis影像数据计算mpdi指数产品，计算公式为：

其中，rv，red和rv，nir分别是红光和近红外波段的植被反射率；fv是植被盖度；m是土壤线斜率；rred是大气校正后的红光波段反射率；rnir是大气校正后的近红外波段反射率。

至此，得到河北省2018年1km分辨率的降雨、ep、mpdi、ndvi和dem数据集，其中ndvi数据采用modis产品，并认为在16天的时间尺度上ndvi值相对稳定。

步骤b、采集地表土壤墒情监测数据，构建基于上述各影响因子的地表土壤含水量神经网络模拟模型(如图2所示)，模拟得到时空连续的地表土壤含水量产品；

采集河北省2018年地表土壤墒情站点的土壤含水率监测数据，观测站点数量约180个，观测频次为每11天观测一次，观测时段为3月～10月，观测深度为10cm；

根据各土壤墒情站点位置，获取相应坐标的降雨、ep、mpdi、ndvi和dem数据；

以各影响要素数据为输入，以土壤含水量观测值为输出，构建神经网络模型，如图3所示，本研究构建的神经网络模型在训练期的相关系数为0.7，在预测期的相关系数为0.5；

利用构建的神经网络模型，对无土壤墒情监测位置的地表土壤含水量进行模拟，得到2018年河北省时空连续的地表土壤含水量产品(段浩等，2021)。

步骤c、基于冠层阻力参数化模型，耦合土壤含水量数据，解析冠层最小气孔阻力与冠层阻力的关系，并基于一般形式penman-monteith公式解析地表阻力，构建冠层气孔阻力与地表阻力的关联；

以河北省石津灌区为例进行gsx的计算。采集石津灌区2018年modis冠层叶面积指数(lai)数据，并利用石津灌区矢量文件进行剪裁。通过日照时数和lai数据，计算分项f，计算公式为

其中，k↓是到达冠层顶部的太阳短波辐射(w/m2)，k↓dbl为辐射临界值

利用步骤b中得到石津灌区2018年土壤含水量计算分项f2，计算公式为：

其中，θcap、θwilt分别为田间持水量和凋萎含水量，与土壤质地有关

利用气温、相对湿度、最高气温、最低气温数据计算分项f3和f4，计算公式为：

f3＝1-g(esat-ea)式(5)

f4＝(1-1.6*10^-3(298-ta)²)⁴式(6)

其中，g是植被系数，为常数。

利用气象和dem数据计算土壤阻力rs，进而求得冠层阻力rc，计算公式为：

其中，ra为空气动力学阻力，λ为汽化潜热，ρ为空气密度，cp为空气定压比热；

将各分量代入式(9)中可得冠层最小气孔阻力rcmin

其中，rcmax是冠层最大气孔阻力，为常数。

进而求得区域尺度的最大气孔导度，计算方法为：

如图4所示，为基于彭曼公式解析得到的地表阻力参数产品，单位为s/m。在此基础上，为计算区域尺度的冠层阻力参数奠定基础。

如图5所示，为本实施例基于遥感反演得到的区域尺度上1km空间分辨率的最大气孔导度参数产品，可基于本实施例所述方法实现时空连续最大气孔导度参数的计算，为增强蒸散发的反演机理提供支撑。

本领域的技术人员将意识到，这里所述的实施例是为了帮助读者理解本发明的实施方法，应被理解为本发明的保护范围并不局限于这样的特别陈述和实施例。本领域的普通技术人员可以根据本发明公开的这些技术启示做出各种不脱离本发明实质的其它各种具体变形和组合，这些变形和组合仍然在本发明的保护范围内。