一种基于拱效应理论的边坡稳定性范围确定方法

本发明属于露天开采的技术领域，尤其涉及一种基于拱效应理论的边坡稳定性范围确定方法。

背景技术：

我国露天煤矿中软岩露天煤矿占比较大，且大多有井下开采记录。无论是受采空区影响的土质边坡还是岩质边坡，坡体中支撑拱的存在都是影响边坡的稳定的重要因素。在土力学领域，土拱是用来描述应力转移的一种现象，这种应力转移是通过土体抗剪强度的发挥而实现的。太沙基(1936)通过活动门试验证实了土拱效应的存在。

土拱效应是岩土工程中一个很普遍的现象，很多学者对活动门模型进行了试验和数值研究，研究结果己被用于很多地下结构的设计中。土层中的拱作用的产生与拱结构物不一样，拱结构是把材料制成拱形状，在荷载作用下发挥其承受压力的作用；而土拱有其自身的形成过程：在荷载或自重的作用下，土体发生压缩和变形，从而产生不均匀沉降，致使土颗粒间产生互相“楔紧”的作用，于是在一定范围土层中产生“拱效应”。正是由于土拱作用所带来的影响，把作用在拱体上的载荷传递到拱脚及其周围的稳定土层中去，最终导致土体中的应力重新分布。需要指出的是，土拱效应是用来对土体中应力转移的现象进行描述的，而此种应力传递的过程是通过对土体滑移面上产生的抗剪强度的调用进行实现的。

虽然已有大量研究成果表明土拱效应普遍存在于支挡结构、管道工程等实际工程中，当土体位移模式不同时，土拱效应引起的应力偏转程度和对边坡变形造成的影响也不尽相同，常见的边坡变形破坏形式主要包括崩塌、蠕动变形、滑坡以及松动张弛四种类型，flac数值模拟软件来模拟边坡的动态过程。需要一种边坡稳定性范围确定方法，将从土拱效应理论出发，研究边坡的变形破坏，从而对边坡的稳定性范围进行界定。

技术实现要素：

基于以上现有技术的不足，本发明所解决的技术问题在于提供一种基于拱效应理论的边坡稳定性范围确定方法，基于拱效应理论，提出一种新的方法研究软岩边坡变形破坏机制，对边坡稳定性范围进行界定，为保证矿区安全生产具有重要的实践指导意义。

为了解决上述技术问题，本发明通过以下技术方案来实现：

本发明提供一种基于拱效应理论的边坡稳定性范围确定方法，包括以下步骤：

s1：将坡脚最不利原生层面裂隙作为其潜在滑面，采场边坡近似于竖直状态，把基坑放坡与台阶影响当作其安全储备；

s2：把边坡的下滑分力视为均布荷载，拱顶两侧过渡区域的下滑力以及由于土体的自重对支撑拱稳定性产生的影响忽略不计，将拱效应简化成沿着深度方向的平面问题；

s3：拱轴线形状近似等化成抛物线，两个支撑拱脚净距作为其跨度；

s4：针对红粘土边坡，其坡体内强度较高的区域的分布；当支撑拱跨度大于土体中支撑拱的极限跨度时，拱效应消失，无法获得足够的抗滑力用来阻滞坡体的滑移；当支撑拱跨度小于土体中支撑拱的极限跨度时，土体内存在拱效应，可以阻滞坡体的滑移甚至塌陷，维持边坡暂时的稳定；

s5：支撑拱脚宽度与拱圈厚度的关系图。

可选的，在步骤s4中，土体中支撑拱的极限跨度lmax的表达式:

式中：h为地表边坡至拱圈外缘处的垂直距离；

h1为土体中土洞的高度；

γ为土体的容重；

kα为土压力系数；

c为黏聚力；

为内摩擦角；

h+h+h1为土拱拱脚处至地面的距离。

进一步的，在步骤s5中，拱圈厚度可表示为：

h＝kωsinα

式中：h为拱圈厚度；

ω为支撑端拱脚处宽度；

α为拱轴线处切线与x轴的夹角；

k为修正系数。

由上，本发明的基于拱效应理论的边坡稳定性范围确定方法基于土拱效应理论，经过土拱效应数学模拟计算，进而得出边坡的最大滑塌高度。应用此成果在采动作用下，对边坡稳定性影响范围进行界定，确定其安全距离，从而指导工程实际，对露天矿安全有非常重要的意义。

上述说明仅是本发明技术方案的概述，为了能够更清楚了解本发明的技术手段，而可依照说明书的内容予以实施，并且为了让本发明的上述和其他目的、特征和优点能够更明显易懂，以下结合优选实施例，并配合附图，详细说明如下。

附图说明

为了更清楚地说明本发明实施例的技术方案，下面将对实施例的附图作简单地介绍。

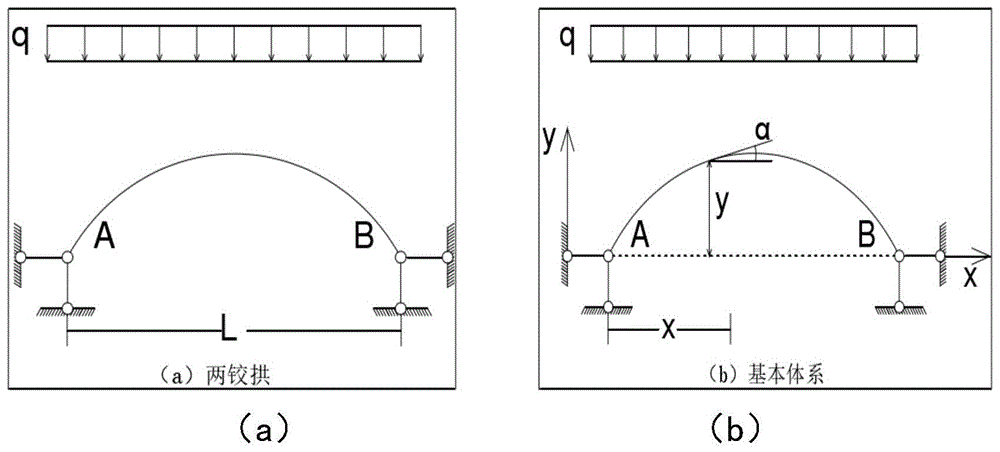
图1为两铰拱计算示意图，其中(a)为两铰拱，(b)为基本体系；

图2为拱脚宽度和拱脚厚度关系示意图；

图3为采空区影响下边坡分区示意图。

具体实施方式

下面结合附图详细说明本发明的具体实施方式，其作为本说明书的一部分，通过实施例来说明本发明的原理，本发明的其他方面、特征及其优点通过该详细说明将会变得一目了然。在所参照的附图中，不同的图中相同或相似的部件使用相同的附图标号来表示。

如图1至图3所示，本发明的基于拱效应理论的边坡稳定性范围确定方法包括以下步骤：

1)土质边坡土体为均质的厚层土体，土层的走向大体和边坡的展布方向保持一致，将坡脚最不利原生层面裂隙作为其潜在滑面，采场边坡近似于竖直状态，把基坑放坡与台阶影响当作其安全储备；

2)把边坡的下滑分力视为均布荷载，拱顶两侧过渡区域的下滑力以及由于土体的自重对支撑拱稳定性产生的影响忽略不计，将拱效应简化成沿着深度方向的平面问题；

3)拱轴线形状近似等化成抛物线，两个支撑拱脚净距作为其跨度，令：

y＝ax²+bx(1-1)

式中：a，b为待定参数；

x—沿拱跨度方向的横坐标，m；

y—任意拱轴截面x处的纵坐标，m。

4)拱脚是与红粘土边坡相互垂直的横向边坡，拱轴线和拱脚宽度共同决定拱圈的厚度，沿拱轴方向处相同；且拱的内力分布情况可根据两铰拱来分析计算(其示意图如图1所示)；

5)针对在采空区影响条件下，土体中支撑拱的极限跨度lmax的表达式:

式中：h—地表边坡至拱圈外缘处的垂直距离，m；

h1—土体中土洞的高度，m；

γ—土体的容重，kn/m³；

kα—土压力系数，

c—黏聚力，kpa；

—内摩擦角。

(h+h+h1)—土拱拱脚处至地面的距离，m。

6)针对红粘土边坡，其坡体内强度较高的区域的分布，即支撑拱的跨度l的值是确定的；当支撑拱跨度l>lmax时，拱效应消失，无法获得足够的抗滑力用来阻滞坡体的滑移；当支撑拱跨度l≤lmax时，土体内存在拱效应，可以阻滞坡体的滑移甚至塌陷，维持边坡暂时的稳定。在对支撑拱跨度研究的基础上，定义边坡的安全系数：

式中：lmax—支撑拱所能承受的最大跨度。

当fs≤1时，边坡处于稳定状态；当fs＞1时，边坡处于不稳定状态。

7)支撑拱脚宽度与拱圈厚度的关系图(如图2所示)，分析可知，拱圈厚度可表示为：

h＝kωsinα(1-4)

式中：h—拱圈厚度，m；

ω—支撑端拱脚处宽度，m；

α—拱轴线处切线与x轴的夹角，°；

k—修正系数。

需要指明的是，式(1-4)中的修正系数k的建议取值是通过宋锦虎等学者进行的相关试验并结合《岩土工程勘察规范》得到的，k的取值如下：

其中h0为土拱拱脚处至地面的距离，m；d为采空区高度，m；由于该区域红粘土的平均厚度是50m，最大厚度约为70m，而煤层的平均厚度12m，即是采空区的最大高度d约为12m，因此k的取值为0.9。

经分析整理得拱圈厚度h可表示为：

假设水平推力f与支座反作用力f’相等，即：

f＝f’(1-6)

以变形协调原理为基础，经分析可得：

式中：y—任一截面处的纵坐标，m；

mp—均布荷载q作用下梁的弯矩；

l—支撑拱跨度，m；

α—拱轴线处切线与x轴的夹角，°；

e—土体的弹性模量，gpa；

i—土拱截面惯性矩，m⁴；

a—拱圈截面积，m²；

h—拱圈厚度，m；

s—沿拱轴的弧段长度，m。

其中：

在工程实践中，土拱多以扁平拱居多，其拱高与跨度比，即：f：l的值多小于13，计算时可取ds＝dx。将式1-1、式1-8、式1-9以及式1-10带入式1-7，经积分化简得并整理得到：

其中：m1＝2b³l²；m2＝20arctan(b)。

土拱轴线的确定结合上述分析以及计算整理可知参数a、b的表达式：

其中：

因此，得到了土拱轴线的关系式为：

y＝ax²+bx

即：

采空区影响范围的确定当红粘土边坡土拱轴线确定后，基于拱圈厚度，得到拱圈内缘线及外缘线的关系式，它们分别为：

(1)拱圈内缘线：

(2)拱圈外缘线：

通过对拱圈内缘线、拱圈外缘线及采空区的研究分析，将红粘土边坡划分成4个区域(见图3)，它们依次分别为拱外侧区、过渡区、拱圈区以及拱内侧区。

由x＝l/2，可以得到最大的滑塌高度

以上所述是本发明的优选实施方式而已，当然不能以此来限定本发明之权利范围，应当指出，对于本技术领域的普通技术人员来说，在不脱离本发明原理的前提下，还可以做出若干改进和变动，这些改进和变动也视为本发明的保护范围。