一种用于模拟材料开裂的相场模型局部化自适应算法的制作方法

1.本发明属于计算力学及材料科学领域，具体的说，本发明涉及一种用于模拟材料开裂的相场模型局部化自适应算法。


背景技术：

2.相场模型作为基于有限元的新兴弥散方法，在模拟材料的断裂破坏时具有着众多优势，近年来逐渐被大量应用于脆性、塑性、晶体等各类固体材料的分析和研究中。相场模型的主要任务之一是对材料破坏的裂纹扩展路径进行预测，为了达到模拟的精确度，需要对计算域进行精细的网格划分，并且由于将裂纹进行了弥散化处理，因此需要求解的控制方程更为复杂，存在求解的过程计算量大的问题，对计算设备等有着很高的要求，从而使其应用范围受到限制，如何在能够利用相场模型的优势的同时尽可能降低相场模型的计算规模一直是一个难以解决的问题。
3.本发明主要解决相场模型在材料裂纹扩展时计算规模过大及功能受限的问题。
4.相场模型一直致力于对材料断裂过程的精确预测模拟，而其庞大的计算量一直是阻碍其发展的主要因素之一，自适应方法是解决此难题的一个有效思路。而目前已经发展的自适应模型绝大多数都是关注于网格的细化过程，尚未有人从控制方程入手，因此本发明提供了一种新的思路，通过避免不必要的方程求解来达到降低计算量的目的。


技术实现要素：

5.本发明的目的在于，为相场模型模拟裂纹扩展提供一种局部化自适应方法。
6.本发明提供的技术方案如下：
7.本发明提供一种用于模拟材料开裂的相场模型局部化自适应算法，包括以下步骤：
8.步骤一：对待测材料进行单轴拉伸试验获得该方法所需材料参数，包括如下参数：
①
抗拉强度，
②
单轴拉伸能量释放率，
③
弹性模量，
④
泊松比；
9.步骤二：采用有限元软件建立有限元二维或者三维数值模型，将测得的材料参数代入建立的有限元模型，并根据欲模拟的实际破坏过程对数值模型施加一定的边界条件；
10.步骤三：利用最小势能原理建立相场模型的控制方程：将材料的弹性体能分为弹性应变能和裂纹表面能以使计算过程能够考虑裂纹扩展，引入相场变量表达材料的破坏程度从而将裂纹表面能正则化，进而对能量表达式进行变分，得到弱积分形式的如下方程：
[0011][0012]
其中：s为相场变量，ε为应变张量，σ(u,s)为应力张量，γ(s,
▽
s)为裂纹表面密度函数，是一个被约束的有限区域，其边界为是一个被约束的有限区域，其边界为为位移
边界条件，为应力边界条件，为裂缝的集合，u为位移，为外部面力，g
c
为能量释放率，ψ为能量密度函数，n为边界的单位外法向量，将公式(1)进行拆解分析，进而得到相场断裂模型的控制方程为：
[0013]
divσ＝0
ꢀꢀꢀ
(2)
[0014][0015]
且边界条件为
[0016][0017][0018]
其中：公式(2)为为弹性方程，公式(3)为裂纹演化方程；
[0019]
步骤四：建立相场模型的局部化自适应判断准则，用以判断材料的破坏状态，并根据是否满足局部化自适应准则，将整体模拟区域分为局部裂纹扩展区域和材料完整区域，以对两个区域采用不同的策略求解；
[0020]
步骤五：进行牛顿法对模型进行迭代求解：在每一次迭代过程中，进行整体
‑
局部交错求解，即整体进行弹性方程进行求解得到位移场u，在局部裂纹扩展区代入得到的位移场进行裂纹演化方程求解得到相场s，再采用局部化自适应准则进行判断，将满足破坏损伤条件的区域加入到局部裂纹扩展区，继而将相场s代入到弹性方程进行下一次迭代过程，直到满足收敛条件。
[0021]
进一步，步骤三所述的控制方程分为弹性方程和裂纹演化方程，其中弹性方程反映材料在加载过程中的应力
‑
应变响应，需要在整体的模拟区域包括材料完整区域和裂纹扩展区进行求解，而裂纹演化方程反映裂纹的发展过程，只需要在材料发生损伤破坏的局部区域——即裂纹扩展区进行求解，从而避免传统方法在整体区域求解裂纹演化方程而造成的大量计算资源浪费。
[0022]
进一步，步骤三中公式(3)所述的裂纹表面密度函数γ(s,
▽
s)通过如下公式计算：
[0023][0024]
其中：l0为表征裂纹弥散化宽度的正则化长度尺度，α(s)为几何裂纹函数，且
[0025]
在相场模型中，需要对弹性体的弹性势能进行退化，以模拟裂纹的发展，其退化形式为
[0026]
ε
s
＝∫
ω
ψ(ε,s)dω
ꢀꢀꢀ
(7)
[0027][0028]
其中：ε
s
为退化后的弹性体的弹性势能，ψ(ε,s)为退化后的弹性势能的能量密
度，ε(u)为应变张量，ω(s)为退化函数，为未退化的拉性能量密度，为剩余的能量密度。
[0029]
一般情况下，退化函数的形式为：
[0030][0031]
其中：幂指数p＞0，q(s)≥0为一个指数函数，进而公式(3)又可以写成如下形式：
[0032][0033]
然而传统的相场模型是在整个计算域中对弹性应变能进行退化，进而在整体上求解裂纹演化方程，然而在实际中仅需要对裂纹扩展的区域(即相场变量s＞0的部分)进行能量退化。因此这里对能量退化的过程和区域进行改进，在裂纹扩展的区域采用公式(8)进行能量退化，而在材料完好的区域采用下面公式：
[0034][0035]
进一步，为了跟踪在加载过程中的局部裂纹扩展区域的动态发展过程，提出高效的局部区域划分准则以实时更新裂纹扩展区域，所述步骤四中区域划分的局部化自适应准则如式(5)所示：
[0036][0037]
其中，σ
c
、ε
c
、分别为临界拉应力、临界拉应变及拉性临界能量密度；当某一点x的相场值s
*
(x)、未退化的主拉应力值σ0(x)、主拉应变值ε(x)、未退化的拉性能量密度任意一个变量大于设定的临界值时，即认为此点在裂纹扩展区域；否则，此点在材料完好区域,从而只将满足自适应准则的区域进行裂纹演化方程求解，实现整体
‑
局部交错求解，进而大大减少计算量。
[0038]
每计算一个荷载步或进行一次迭代，则对上述准则进行一次判定，从而达到局部裂纹扩展区动态自适应更新的目的，为了进一步提高计算模拟效率，也可以牺牲少许计算精度，采取上述四个判定法则中任意一个作为局部化自适应准则。
[0039]
进一步，通过考虑一维长杆的单轴受拉破坏，可以推出裂纹演化方程(3)的另一种形式：
[0040][0041]
进而所述裂纹演化的各临界值可以通过以下公式确定：
[0042][0043][0044]
其中：通过公式(14)可以得到和ε
c
，通过公式(15)可以得到σ
c
。
[0045]
进一步，对于裂纹扩展的区域，为了防止模拟过程中裂纹愈合从而造成错误结果，需要引入在计算过程中只能增大不能减小的历史场变量历史场变量可以采取以下几种形式的任意一种，
[0046][0047][0048][0049]
其中：t为数值模拟过程中所进行到的最后一个时间步，τ为[0,t]内的任意时间步，为位于位置x的点在时间t的历史场，σ0(x,τ)、ε(x,t)、分别代表位于位置x的点在时间t的最大主应力、最大主应变及拉性应变能，进而裂纹演化方程公式(3)或者公式(10)可以在计算过程中可以采用如下公式代替：
[0050][0051][0052][0053]
采用公式(19)、(20)、(21)中的任意一个公式取代裂纹演化方程即可阻止裂纹发展过程中产生不应该出现的裂缝闭合现象。
[0054]
进一步，步骤五所述的迭代求解法中，为了保证计算结果的精确性，在每个荷载步采用牛顿法迭代求解，即对控制方程(2)和裂纹演化方程(19)或(20)或(21)进行整体
‑
局部交错求解，直到应变的残余误差满足收敛条件：
[0055]
ε＜ε1ꢀꢀꢀ
(22)
[0056]
其中：ε为每一个迭代步求得的应变残余误差，ε1为设定的残余误差临界值，可设为10
‑8～10
‑6。
[0057]
将每一荷载步逐步求解，即可得到模拟对象的裂纹演化情况。
[0058]
本算法可以通过ansys、abaqus、matlab、comsol等大型商业软件二次开发实现，在求解过程中，既可以采用迭代算法，也可以采用分布解耦算法，具有很强的灵活性与收敛性，可以被广泛推广到其他数值模拟过程中去。
[0059]
与现有数值模拟技术相比，本发明具有以下有益效果：
[0060]
本发明利用了局部自适应技术对相场模型进行改进来模拟裂纹的扩展过程，突破了传统方法计算量过大，耗时过长，对于复杂的模型难以模拟的问题。通过将模拟区域划分为裂纹扩展区域和材料完好区域，实现控制方程求解的局部化；提供了有效的局部化自适应准则，可以对裂纹扩展区域进行精准划分；并且计算结果能够保证计算的精确度。该算法大大减少了相场模型的计算量，能够极大地节省计算成本。本发明实施过程简单，实用性强，灵活度高，并可以被广泛地推广。
附图说明
[0061]
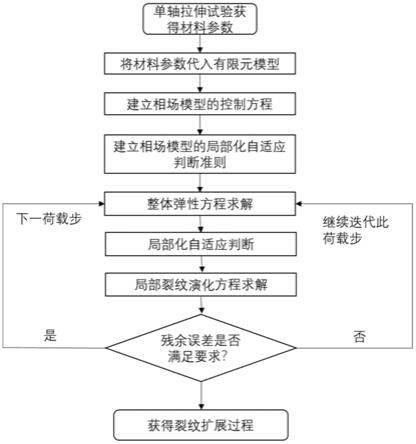
图1是所述的相场模型局部化自适应算法实施技术路线图；
[0062]
图2是所述的方板试件的几何结构和网格划分；
[0063]
图3是所述的局部化自适应裂纹扩展模拟结果；其中，黑色区域部分为裂纹扩展区，即解裂纹演化方程的区域；图3(a)为l0＝0.01mm,h＝0.002mm非迭代算法，图3(b)l0＝0.01mm,h＝0.002mm迭代算法；图3(c)l0＝0.005mm,h＝0.001mm非迭代算法，图3(d)l0＝0.005mm,h＝0.001mm迭代算法；
[0064]
图4是所述的局部化自适应算法与传统算法计算的荷载
‑
位移曲线对比。
具体实施方式
[0065]
为了对本发明的技术特征、目的和效果有更加清楚的理解，现对照附图详细说明本发明的具体实施方式。
[0066]
实施例
[0067]
一种用于模拟材料开裂的相场模型局部化自适应算法(图1所示)，模拟步骤如下：
[0068]
步骤一：进行单轴拉伸试验获得该方法所需材料参数，包括以下参数：(1)弹性模量e＝191.1gpa，(2)泊松比μ＝0.183，(3)单轴拉伸能量释放率g
c
＝2.7n/mm(4)抗拉强度f
t
＝2445.42mpa；
[0069]
步骤二：采用有限元软件建立有限元二维或者三维数值模型，将测得的材料参数代入建立的有限元模型，并根据欲模拟的实际破坏过程对数值模型施加一定的边界条件，此算例的边界条件为方板下边界施加固定约束，上边界施加水平向右的等速位移，位移施加速率为每个荷载步δu＝0.5
×
10
‑5mm；
[0070]
步骤三：利用最小势能原理建立相场模型的控制方程：将材料的弹性体能分为弹性应变能和裂纹表面能使计算过程能够考虑裂纹扩展，引入相场变量表达材料的破坏程度从而将裂纹表面能正则化，进而对能量表达式进行变分，得到弱积分形式的如下方程：
[0071]
[0072]
其中：s为相场变量，ε为应变张量，σ(u,s)为应力张量，γ(s,
▽
s)为裂纹表面密度函数，是一个被约束的有限区域，其边界为是一个被约束的有限区域，其边界为为位移边界条件，为应力边界条件，为裂缝的集合，u为位移，为外部面力，g
c
为能量释放率，ψ为能量密度函数，n为边界的单位外法向量，将公式(1)进行拆解分析，进而得到相场断裂模型的控制方程为：
[0073]
divσ＝0
ꢀꢀꢀ
(2)
[0074][0075]
且边界条件为
[0076][0077][0078]
其中：公式(2)为控制方程的弹性部分(可称为弹性方程)，公式(3)为控制方程的裂纹演化部分(可称为裂纹演化方程)；
[0079]
步骤四：建立相场模型的局部化自适应判断准则，用以判断材料的破坏状态，并根据是否满足局部化自适应准则，将整体模拟区域分为局部裂纹扩展区域和材料完整区域，以对两个区域采用不同的策略求解；
[0080]
步骤五：进行牛顿法对模型进行迭代求解：在每一次迭代过程中，进行整体
‑
局部交错求解，即整体进行弹性方程进行求解得到位移场u，在局部裂纹扩展区代入得到的位移场进行裂纹演化方程求解得到相场s，再采用局部化自适应准则进行判断，将满足破坏损伤条件的区域加入到局部裂纹扩展区，继而将相场s代入到弹性方程进行下一次迭代过程，直到满足收敛条件。
[0081]
步骤三所述的控制方程分为弹性方程和裂纹演化方程，其中弹性方程反映材料在加载过程中的应力
‑
应变响应，需要在整体的模拟区域包括材料完整区域和裂纹扩展区进行求解，而裂纹演化方程反映裂纹的发展过程，只需要在材料发生损伤破坏的局部区域——即裂纹扩展区进行求解，从而避免传统方法在整体区域求解裂纹演化方程而造成的大量计算资源浪费。
[0082]
步骤三中公式(3)所述的裂纹表面密度函数γ(s,
▽
s)通过如下公式计算：
[0083][0084]
其中：l0为表征裂纹弥散化宽度的正则化长度尺度，α(s)为几何裂纹函数，且
[0085]
在相场模型中，需要对弹性体的弹性势能进行退化，以模拟裂纹的发展，其退化形式为
[0086]
ε
s
＝∫
ω
ψ(ε,s)dω
ꢀꢀꢀ
(7)
[0087][0088]
其中：ε
s
为退化后的弹性体的弹性势能，ψ(ε,s)为退化后的弹性势能的能量密度，ε(u)为应变张量，ω(s)为退化函数，为未退化的拉性能量密度，为剩余的能量密度。
[0089]
一般情况下，退化函数的形式为：
[0090][0091]
其中：幂指数p＞0，q(s)≥0为一个指数函数，进而公式(3)又可以写成如下形式：
[0092][0093]
然而传统的相场模型是在整个计算域中对弹性应变能进行退化，进而在整体上求解裂纹演化方程，然而在实际中仅需要对裂纹扩展的区域(即相场变量s＞0的部分)进行能量退化。因此这里对能量退化的过程和区域进行改进，在裂纹扩展的区域采用公式(8)进行能量退化，而在材料完好的区域采用下面公式：
[0094][0095]
为了跟踪在加载过程中的局部裂纹扩展区域的动态发展过程，提出高效的局部区域划分准则以实时更新裂纹扩展区域，所述步骤四中区域划分的局部化自适应准则如式(5)所示：
[0096][0097]
其中，σ
c
、ε
c
、分别为临界拉应力、临界拉应变及拉性临界能量密度；当某一点x的相场值s
*
(x)、未退化的主拉应力值σ0(x)、主拉应变值ε(x)、未退化的拉性能量密度任意一个变量大于设定的临界值时，即认为此点在裂纹扩展区域；否则，此点在材料完好区域,从而只将满足自适应准则的区域进行裂纹演化方程求解，实现整体
‑
局部交错求解，进而大大减少计算量。
[0098]
每计算一个荷载步或进行一次迭代，则对上述准则进行一次判定，从而达到局部裂纹扩展区动态自适应更新的目的，为了进一步提高计算模拟效率，也可以牺牲少许计算精度，采取上述四个判定法则中任意一个作为局部化自适应准则。
[0099]
通过考虑一维长杆的单轴受拉破坏，可以推出裂纹演化方程(3)的另一种形式：
[0100][0101]
进而所述裂纹演化的各临界值可以通过以下公式确定：
[0102][0103][0104]
其中：通过公式(14)可以得到和ε
c
，通过公式(15)可以得到σ
c
。
[0105]
对于裂纹扩展的区域，为了防止模拟过程中裂纹愈合从而造成错误结果，需要引入在计算过程中只能增大不能减小的历史场变量历史场变量可以采取以下几种形式的任意一种，
[0106][0107][0108][0109]
其中：t为数值模拟过程中所进行到的最后一个时间步，τ为[0,t]内的任意时间步，为位于位置x的点在时间t的历史场，σ0(x,τ)、ε(x,t)、分别代表位于位置x的点在时间t的最大主应力、最大主应变及拉性应变能，进而裂纹演化方程公式(3)或者公式(10)可以在计算过程中可以采用如下公式代替：
[0110][0111][0112][0113]
采用公式(19)、(20)、(21)中的任意一个公式取代裂纹演化方程即可阻止裂纹发展过程中产生不应该出现的裂缝闭合现象。
[0114]
步骤五所述的迭代求解法中，为了保证计算结果的精确性，在每个荷载步采用牛顿法迭代求解，即对控制方程(2)和裂纹演化方程(19)或(20)或(21)进行整体
‑
局部交错求解，直到应变的残余误差满足收敛条件：
[0115]
ε＜ε1ꢀꢀꢀ
(22)
[0116]
其中：ε为每一个迭代步求得的应变残余误差，ε1为设定的残余误差临界值，可设为10
‑8～10
‑6。
[0117]
将每一荷载步逐步求解，即可得到模拟对象的裂纹演化情况。
[0118]
本实施例共计算了四种情况：(1)l0＝0.01mm，h＝0.002mm，采用分布解耦算法；(2)l0＝0.01mm，h＝0.002mm，采用迭代算法；(3)l0＝0.005mm，h＝0.001mm，采用分布解耦算法；(4)l0＝0.005mm，h＝0.001mm，采用迭代算法。
[0119]
通过图3和图4可知，深色区域为裂纹演化区域，其在计算过程中不断动态发展，该自适应算法即使大幅度降低了计算量，依然能保证裂纹扩展路径和力学响应的精确模拟。
[0120]
综上所述，本发明是一种高效、稳定、实施流程清晰且适应性强的计算方法，该发明可为材料在各种裂纹扩展模拟问题提供理论与技术支撑，促进有限元及相场模型在材料破坏分析中的应用。
[0121]
以上所述，仅为本发明较佳的具体实施方式，但本发明保护的范围并不局限于此，任何熟悉本技术领域的技术人员在本发明揭露的技术范围内所做的任何修改，等同替换和改进等，均应包含在发明的保护范围之内。