一种移动边缘计算中的用户计算任务卸载方法

本发明属于通信技术领域，具体涉及一种移动边缘计算中的用户计算任务卸载方法。

背景技术：

随着5g时代的到来，与5g技术相关的应用场景，如物联网、增强现实、虚拟现实等日益受到人们的广泛关注。这些以时延敏感和计算密集为主要特点的新兴业务对移动智能终端产生极大的挑战，由于现有的移动智能终端其计算能力有限，如果终端自身执行这些的任务，会导致较大的时延和能耗。于是，研究者们纷纷把目光聚焦于移动边缘计算(mobileedgecomputing，mec)，通过无线网络将终端任务卸载到边缘服务器执行，大大降低任务的完成时间，以实现低时延、低能耗信息服务的目标。

移动边缘计算卸载成为当前研究的热点，近年来，越来越多的学者关注mec卸载决策问题。目前我们将任务卸载模型划分为可拆分任务卸载模型和不可拆分任务卸载模型，可拆分任务卸载模型指用户可以将任务部分卸载或全部卸载，不可拆分任务卸载模型指的是用户只能选择将任务全部本地处理或全部卸载给边缘服务器处理。目前可拆分任务卸载模型下大都采用博弈论，但这种方法没有考虑应用程序间的关联性，还有不少学者将有先后顺序依赖关系的任务用有向无环图(directedacyclicgraph，dag)描述，但对时延优化较少，调度效率不高并且负载不均衡，尚且满足不了时延敏感型应用的需求。虽然不可拆分任务卸载模型可以处理依赖性应用，但任务的完成时间却远远不如可拆分任务卸载模型。

现有的专利文件中，如cn110928654a公开的一种边缘计算系统中分布式的在线任务卸载调度方法，其基于计算任务的异构性和随机性，移动智能设备和边缘服务器的计算资源有限性，以及移动智能设备的能耗问题，针对具有三层体系结构的边缘计算系统提出一个任务卸载调度算法，使得所有任务的平均完成时延最小化，但并未考虑计算任务的前后顺序依赖关系；另如cn109992419a公开的一种优化的协同边缘计算低延迟任务分配卸载方法，也仅是将任务划分为子任务后，分别求得各个子任务的传输和计算的总时延，再求得整个任务总时延最低时的卸载最优解，也并未考虑计算任务的依赖关系，同时实现过程中计算求解任务繁重，极易出错，实现效果并不理想。

技术实现要素：

为了减少计算卸载时延，本发明提出一种移动边缘计算中的用户计算任务卸载方法。该方法针对有先后顺序依赖关系的应用，结合dag，将不同子任务卸载到边缘服务器，大大降低整体任务的完成时间，同时保证用户的公平性和负载均衡性。

一种移动边缘计算中的用户计算任务卸载方法，包括如下步骤：

步骤1，定义边缘计算服务器集合，并用户的应用程序划分子任务，得到子任务集合；

步骤2，计算子任务卸载的相关参数，即完成每个子任务所需要的时延和能耗。

步骤3，构建任务关系图，建立其与待卸载子任务之间的联系，得到初始任务关系图；

步骤4，根据步骤3构建的初始任务关系图，开始进行子任务在不同边缘服务器上的计算卸载过程，包括任务关系图的更新和边缘服务器的选择，转入步骤5；

步骤5，读取初始任务关系图中子任务节点和各有向边的权值，计算子任务的执行时间方差和子任务之间的通信时延，同时考虑子任务间的内在执行顺序，对各子任务赋予卸载优先级；

步骤6，根据步骤5计算的通信时延，求出关键路径，该关键路径定义为从入口节点到出口节点的最长路径；

步骤7，进行任务卸载与任务关系图更新策略：对当前子任务，判断其前驱节点是否关键路径上的子任务节点，并且满足任务复制卸载条件；若不满足则在能耗约束下，根据最早完成时间算法选择边缘服务器，并在此边缘服务器上计算执行；否则，首先根据最早完成时间算法选择边缘服务器，然后将当前子任务的前驱子任务节点，即关键路径上的节点的内容复制到当前子任务选择的服务器中，与当前子任务的内容一并计算执行；删除其前驱子任务节点，更新任务关系图，保留该子任务的计算结果，同时计算子任务开始执行时间，子任务完成时间以及卸载决策向量；

步骤8，同时进行应用程序本地计算和边缘计算，子任务集合中的子任务卸载完成后求出总体完成时间和相应的卸载决策。

进一步地，步骤1中，定义边缘计算服务器集合为s＝{s1,s2...sj...sn}∪{s0}，其中n表示边缘服务器的数量，s0表示本地处理器；服务器sj的计算能力用fj表示，j∈{0,1...j...n}，其中f0表示本地处理器的计算能力。用户的应用程序划分为m个子任务，子任务集合为v＝{v1,v2...vi...vm}，其中i表示子任务的标号。每个子任务vi的计算任务属性表示为ti＝{mi,ci,ai}，其中mi表示该子任务的数据量大小，ci表示完成任务vi所需要的cpu周期数，ai表示卸载决策，a＝(a1,a2...ai...am)表示m个子任务的卸载决策向量。

进一步地，步骤2中，计算完成每个子任务所需要的时延和能耗，包括如下步骤：

步骤2a，计算用户和边缘服务器j之间的上行数据速率如下:其中b为信道带宽，qi为传输功率，gi,j为子任务vi与边缘服务器sj之间的信道增益，ω为噪声功率，为来自相同服务器的干扰。

步骤2b，本地计算：

本地计算执行时间为本地能耗为其中δ^l为终端每个cpu周期的能耗。

步骤2c，边缘计算：

边缘计算执行时间为ti,j＝ci/fj，因此为了简化，结合本地计算执行时间，任务执行时间ti,j＝ci/fj，j＝0时为本地计算。传输时间为ωi,j＝mi/ri,j(a)；传输能耗为ei,j＝qimi/ri,j(a)。

进一步地，步骤3中，根据待卸载子任务的先后顺序依赖关系，构建一个有向无环任务关系图g＝{v,e}，描述各个子任务的依赖关系，其中e表示具有先后顺序依赖关系的子任务间的有向边集合，其权值表示两个子任务间的通信数据量，根据步骤2中的相关参数，计算图g子任务节点和各有向边的权值。

进一步地，步骤3构建任务关系图，包括如下步骤：将应用程序分割成若干个子任务，根据子任务的先后顺序依赖关系，将整个应用程序的所有子任务构建成只有一个起点和一个终点的有向无环图，其中指向表示两子任务之间的先后顺序依赖关系，同时指向上标记两子任务之间通信的数据量大小。

进一步地，步骤5子任务卸载优先级排序，包括如下步骤：

步骤5a，计算得到子任务vi的平均执行时间：然后得到子任务vi的平均执行时间方差为同时计算子任务vi和vi′的通信时间：其中bjj″表示服务器sj和sj′之间的带宽，eii′表示子任务vi和vi′间通信的数据量；

步骤5b，根据步骤5a计算得到的参数求子任务vi的卸载优先级其中succ(i)表示子任务vi的后继任务组成的集合，cii′表示子任务vi和vi′的通信时间；按降序顺序对所有子任务的rank(i)值进行排序，即rank(i)值大的子任务优先卸载。

进一步地，步骤6所述关键路径的寻找方法，包括如下步骤：

步骤6a，定义以及其中ranku(i)表示从入口节点计算子任务vi的升秩值，rankd(i)表示从出口节点计算子任务vi的降秩值，succ(i)表示子任务vi的后继任务组成的集合，pred(i)表示子任务vi的前驱任务组成的集合；

步骤6b，计算任务关系图中所有子任务的ranku(i)和rankd(i)值，根据ranku(i)+rankd(i)找到关键路径上的子任务节点。

进一步地，步骤7任务卸载与任务关系图更新策略，包括如下步骤：

步骤7a，首先选取当前任务关系图中具有最大rank(i)值的子任务，判断其前驱节点是否关键路径上的子任务节点，并且若满足任务复制卸载条件，即要满足不等式aft(i,j)＞aft(i,j)′，其中aft(i,j)表示子任务vi卸载到边缘服务器sj上计算执行所需的时间，aft(i,j)′表示将前驱节点复制卸载后，计算执行子任务vi所需的时间；

步骤7b，若条件不成立，则在能耗约束下，根据最小的aft(i,j)将当前子任务vi卸载到对应的边缘服务器sj上，并在此边缘服务器上计算执行；删除其前驱子任务节点，更新任务关系图，保留该子任务的计算结果，同时计算子任务开始执行时间ast(i,j)，子任务完成时间aft(i,j)，以及卸载决策向量a；

步骤7c，若条件成立，首先在能耗约束下根据aft(i,j)选择边缘服务器，然后将当前子任务的前驱子任务节点，关键路径上的节点的内容复制到当前子任务选择的服务器中，与当前子任务的内容一并计算执行；删除其前驱子任务节点，更新任务关系图，保留该子任务的计算结果，同时更新ast(i,j)，aft(i,j)和卸载决策向量a。

进一步地，步骤8所述计算最终完成时间，包括如下步骤：

步骤8a，计算得到子任务最早开始执行时间：其中i和i′是子任务的标号，j和j′是边缘服务器的标号，avail{i,j}是边缘服务器或本地设备sj准备好执行任务的最早时间，即边缘服务器sj空闲，并且空闲时隙足够长以插入子任务i以供执行的最早时间；是子任务vi和vi′的在不同服务器上的数据交换时间，当j＝j′时，

步骤8b，计算子任务最终完成时间：aft(i,j)＝min(ti,j+ast(i,j))；重复步骤7和步骤8，直到卸载完所有任务即可求得最终完成时间，对应的最佳卸载方案保存在向量a中。

本发明与现有技术相比具有如下优点：

1、本发明将应用程序视为可拆分计算卸载，与不可拆分模型相比，大大降低了任务完成时间，更有利于用户做出适合自己行为的选择，同时一定程度上提高了边缘服务器的利用率。

2、本发明在计算卸载的同时考虑能耗约束以实现低时延、低能耗信息服务的目标。

3、本发明的任务排序方面采用执行时间的二次方差作为排序依据更能区分依赖性任务的执行顺序，任务调度方面进行任务复制卸载减少了通信成本，进一步降低了任务完成时间，同时保证各卸载任务的公平性和负载均衡性。

附图说明

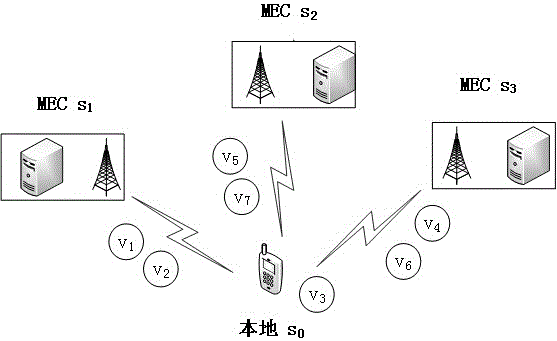
图1是本发明实施例中的网络模型图。

图2是本发明实施例中任务关系图的建立示意图。

图3是本发明实施例中任务关系图的更新示意图。

图4是本发明实施例中方法的实施流程框图。

图5是本发明实施例中任务完成时间随边缘服务器数量变化的仿真结果图。

具体实施方式

下面结合说明书附图对本发明的技术方案做进一步的详细说明。

参见图5，本方法的具体实现步骤如下：

步骤1、定义边缘计算服务器集合为s＝{s1,s2...sj...sn}∪{s0}，其中n表示边缘服务器的数量，s0表示本地处理器；服务器sj的计算能力用fj表示，j∈{0,1...j...n}，其中f0表示本地处理器的计算能力。用户的应用程序划分为m个子任务，子任务集合为v＝{v1,v2...vi...vm}，其中i表示子任务的标号。每个子任务vi的计算任务属性表示为ti＝{mi,ci,ai}，其中mi表示该子任务的数据量大小，ci表示完成任务vi所需要的cpu周期数，ai表示卸载决策，a＝(a1,a2...ai...am)表示m个子任务的卸载决策向量。

步骤2、计算子任务卸载的相关参数，求出完成每个子任务所需要的时延和能耗。

2a)计算用户和边缘服务器j之间的上行数据速率如下:其中b为信道带宽，qi为传输功率，gi,j为子任务vi与边缘服务器sj之间的信道增益，ω为噪声功率，为来自相同服务器的干扰。

2b)本地计算：

本地计算执行时间为本地能耗为其中δ^l为终端每个cpu周期的能耗。

2c)边缘计算：

边缘计算执行时间为ti,j＝ci/fj，因此为了简化，结合本地计算执行时间，任务执行时间ti,j＝ci/fj，j＝0时为本地计算。传输时间为ωi,j＝mi/ri,j(a)；传输能耗为ei,j＝qimi/ri,j(a)。

步骤3、构建任务关系图，建立其与待卸载子任务之间的联系。

根据待卸载子任务的先后顺序依赖关系，构建一个有向无环任务关系图g＝{v,e}，描述各个子任务的依赖关系，其中e表示具有先后顺序依赖关系的子任务间的有向边集合，其权值表示两个子任务间的通信数据量。根据步骤2中的相关参数，计算图g子任务节点和各有向边的权值。

3a)有向无环任务关系图的构建：将应用程序分割成若干个子任务，根据子任务的先后顺序依赖关系，将整个应用程序的所有子任务构建成只有一个起点和一个终点的有向无环图，举例如图2所示。

3b)v1表示该应用程序的初始子任务，v7表示该应用程序的结束子任务。箭头两边的任务节点表示两者的先后顺序依赖关系，如v1→v2表示v1执行完才能执行v2，v2的执行依赖于v1发送的数据；e12＝(v1,v2)＝10表示v1v2间通信的数据量大小。

步骤4、根据步骤3构建的初始任务关系图，步骤5—步骤8详细说明子任务在不同边缘服务器上的计算卸载过程，包括任务关系图的更新和边缘服务器的选择。

步骤5、读取图g子任务节点和各有向边的权值，计算子任务的执行时间方差和子任务之间的通信时延，同时考虑子任务间的内在执行顺序，对各子任务赋予卸载优先级。

5a)计算所有任务的执行时间方差：子任务vi的平均执行时间子任务vi的平均执行时间方差为

子任务vi和vi′的通信时间：其中bjj″表示服务器sj和sj′之间的带宽，eii′表示子任务vi和vi′间通信的数据量。

5b)根据5a)的相关公式求子任务vi的卸载优先级其中succ(i)表示子任务vi的后继任务组成的集合，cii′表示子任务vi和vi′的通信时间。按降序顺序对所有子任务的rank(i)值进行排序，即rank(i)值大的子任务优先卸载。

步骤6、根据步骤5计算的通信时延，求出关键路径。其中关键路径定义为从入口节点到出口节点的最长路径。

6a)定义其中ranku(i)表示从入口节点计算子任务vi的升秩值，rankd(i)表示从出口节点计算子任务vi的降秩值，succ(i)表示子任务vi的后继任务组成的集合，pred(i)表示子任务vi的前驱任务组成的集合。

6b)计算图g中所有子任务的ranku(i)和rankd(i)值，根据ranku(i)+rankd(i)找到关键路径上的子任务节点。

步骤7、任务卸载与图g更新策略：对当前子任务，判断其前驱节点是否关键路径上的子任务节点，并且满足任务复制卸载条件。若不满足，则在能耗约束下，根据最早完成时间算法选择边缘服务器，并在此边缘服务器上计算执行；否则，首先根据最早完成时间算法选择边缘服务器，然后将当前子任务的前驱子任务节点(关键路径上的节点)内容复制到当前子任务选择的服务器中，与当前子任务的内容一并计算执行。删除其前驱子任务节点，更新任务关系图，保留该子任务的计算结果，同时计算子任务开始执行时间，子任务完成时间以及卸载决策向量。

7a)首先选取当前图g中具有最大rank(i)值的子任务，判断其前驱节点是否关键路径上的子任务节点，并且若满足任务复制卸载条件，即要满足不等式aft(i,j)＞aft(i,j)′，其中aft(i,j)表示子任务vi卸载到边缘服务器sj上计算执行所需的时间，aft(i,j)′表示将前驱节点复制卸载后，计算执行子任务vi所需的时间。若条件不成立，则在能耗约束下，根据最小的aft(i,j)将当前子任务vi卸载到对应的边缘服务器sj上，并在此边缘服务器上计算执行。删除其前驱子任务节点，更新任务关系图，保留该子任务的计算结果，同时计算子任务开始执行时间ast(i,j)，子任务完成时间aft(i,j)，以及卸载决策向量a。

7b)若条件成立，首先在能耗约束下根据aft(i,j)选择边缘服务器，然后将当前子任务的前驱子任务节点(关键路径上的节点)内容复制到当前子任务选择的服务器中，与当前子任务的内容一并计算执行。删除其前驱子任务节点，更新任务关系图，保留该子任务的计算结果，同时更新ast(i,j)，aft(i,j)和卸载决策向量a。

7c)图g更新策略示例：根据图2，更新第一个关键路径上的子任务卸载之后的图g。假设该图的关键路径为v1→v4→v5→v7。v1的后继任务有v2，v3，v4，若v1→v2和v1→v4满足复制卸载条件，v1→v3不满足复制卸载条件，则更新图g如图3中的(b)所示，即将v1复制卸载到v2，v4所处的服务器上，而v1→v3不变。v1卸载执行完，把v1的计算结果传给不满足复制卸载条件的任务v3后，即可删除v1。更新结果如图3的(c)所示，其中v3(v1)表示包含v1计算结果的v3。接着卸载关键路径上的下一个子任务节点v4，继续更新图g，直到完成所有子任务。根据此更新策略得到图g的更新：b→c→d→e→f→g。

步骤8、同时进行应用程序本地计算和边缘计算，系统中m个子任务卸载完成后求出总体完成时间和相应的卸载决策。

8a)子任务最早开始执行时间：其中i和i′是子任务的标号，j和j′是边缘服务器的标号，avail{i,j}是边缘服务器(或本地设备)sj准备好执行任务的最早时间，即边缘服务器sj空闲并且空闲时隙足够长以插入子任务i以供执行的最早时间。是子任务vi和vi′的在不同服务器上的数据交换时间，当j＝j′时，

8b)子任务最终完成时间：aft(i,j)＝min(ti,j+ast(i,j))。重复步骤7和步骤8，直到卸载完所有任务即可求得最终完成时间，对应的最佳卸载方案保存在向量a中。

本发明的效果可通过以下仿真进一步验证。

1.实验场景：

随机生成一些dag，每个子任务需要的cpu周期数从100m到500m。子任务的大小在[500,1500]kb，终端的处理能力为50mhz，边缘服务器在[250，1000]mhz。每个应用程序子任务个数为25，边缘服务器个数在1到20个。

2.实验内容与结果：

图5是仿真结果，横坐标是边缘服务器的数量，纵坐标是任务完成时间，pgoa是采用博弈论的方法将任务不划分卸载，实验是仿真一个应用程序，因此是一个定值。defo是可划分卸载，但本文方法明显优于defo，因为本文通过任务复制卸载大大降低了通信成本。

以上所述仅为本发明的较佳实施方式，本发明的保护范围并不以上述实施方式为限，但凡本领域普通技术人员根据本发明所揭示内容所作的等效修饰或变化，皆应纳入权利要求书中记载的保护范围内。