一种用于河流生态修复的曝气控制系统及其控制方法

本发明涉及一种用于河流生态修复的曝气控制系统及其控制方法，属于河流生态修复的技术领域。

背景技术：

河流水体中的溶解氧的浓度，是反应河流污染情况的重要指标。在河流污染治理过程中，首先需要对河流水体的溶解氧含量进行改变。河流的溶解氧浓度是河流耗氧过程和复氧过程共同作用的结果。生态健康的河流，耗氧速率与复氧速率处于平衡状态，河流污染之后，水体中过量的有机物导致河流的耗氧速率增加，溶解氧浓度不断下降，河流的氧平衡被打破，河流出现黑臭等环境问题。随着有机物的减少，耗氧速率逐渐下降，当复氧速率大于耗氧速率时，溶解氧浓度开始回升，河流恢复污染前的状态，这是河流自然的自净过程。然而，由于外源有机物持续输入超出了河流本身的自净能力，需要人为增加河流的复氧速率，曝气技术成为河流污染治理与生态修复工程中提高复氧速率的常用技术。

在河流污染治理与生态修复的工程实践中，采用的曝气控制方式，多是连续曝气或间歇曝气，曝气量多是凭操作人员的经验人为设定，存在曝气不足或过量的问题，会造成能源浪费和运行成本增加。近年，出现了基于实时溶解氧浓度的曝气控制模型，以期解决这个问题。但是，由于难以定义健康河流的溶解氧浓度，这类控制方式取得的实际效果也并不理想。

技术实现要素：

为了解决上述技术问题，本发明提供一种用于河流生态修复的曝气控制系统及其控制方法，其具体技术方案如下：

一种用于河流生态修复的曝气控制系统，包括感知模块、控制模块和曝气模块，所述感知模块用于采集河流概况、河流水质、河流水动力和河流生物四个维度的河流基础数据，所述控制模块用于分析处理感知模块采集到的数据，将其换算成控制曝气模块的参数，并给曝气模块发送控制信号。

进一步的，所述河流概况的数据包括河流宽度、河流深度、水面坡降、河流中弘线长度、河流起止断面距离、城市连接廊道数量、最大的廊道数量、水系节点个数、污染源情况、周围土地利用类型中的一种或多种；

所述河流水质的数据包括水温、溶解氧浓度、氧化还原电位、浊度、氨氮浓度、硝酸盐氮浓度、总氮、总磷、耗氧速率、生物需氧量、化学需氧量中的一种或多种；

所述河流水动力的数据包括河流的流速、流量、剪切力中的一种或多种；

所述河流生物的数据包括微生物、原生动物、后生动物、鱼类、藻类、浮游植物、沉水植物中的一种或多种。

一种用于河流生态修复的曝气系统的控制方法，包括以下步骤：

步骤一：获取河流概况、河流水质、河流水动力和河流生物四个维度的数据，通过人机交互的方式输入控制模块，控制模块对输入数据经过预处理后，输入神经网络模型，计算出通过曝气修复河流的目标值；

步骤二：启动曝气模块，感知模块和控制模块同步开始工作，根据曝气模块启动前输入控制模块的数据，以及感知模块实时监测的数据，每隔六小时计算一次河流最佳曝气量，按公式(1)(2)计算曝气量，向曝气模块发送控制信号，控制曝气的强度和时间；根据感知模块传输给控制模块的数据，实时监控河流曝气情况，维持河流的溶解氧浓度在预期水平；

e(k)＝domeasure(k)-doset/default(k)(2)

其中，q(k)表示曝气量，kp表示e(k)项的系数，ki表示项的系数，kd表示[e(k)-e(k-1)]项的系数，k表示k时刻，e(k)表示k时刻测量值与设置/预设溶解氧浓度值的偏差，e(k-1)表示k-1时刻测量值与设置/预设值的偏差，domeasure(k)表示测量得到的k时刻溶解氧浓度，doset/default(k)表示k时刻曝气器控制模块溶解氧的输入值或预设值；

步骤三：循环步骤二，直至感知模块监测的河流的现状达到神经网络模型得到的曝气修复河流的目标值，停止曝气并通知管理人员。

进一步的，所述步骤一中的神经网络模型，建立方法为：

步骤1：收集基础数据，选取有代表性的河流，收集包括河流曝气修复前后常规理化指标、生物指标，以及河流宽度、深度、功能、周围土地利用类型、污染源情况，至少80组数据；

步骤2：数据预处理，首先剔除明显异常和错误的数据，然后基于公式(3)做共线性分析，剔除共线性高的数据，再用排序算法做进一步降维，将输入指标降低到10个以内；最后，将处理好的数据划分为训练样本集和测试样本集；(随机按7：3划分训练样本集和测试样本集)

其中，r²为决定系数；vif≥20剔除，vif＜20保留；

步骤3：训练神经网络模型，将预处理后的结果作为输入层，将溶解氧浓度、氨氮浓度、化学需氧量、河流耗氧速率、自养生物占比作为输出层，输入层神经元数量与预处理后的指标个数相同，输出层神经元数量为5个；隐含层数量与神经元个数根据神经网络模型的质量进行调整，默认为两层；完成建模后，训练神经网络模型，根据输出结果，评估模型的损失函数，按公式(4)计算平均平方误差mse表示神经网络模型的损失，直至图谱表现为水平直线，判定为符合要求；

其中，h(xⁱ)代表预测的第i个值，yⁱ代表实际的第i个值；m1为测试集样本数量；

步骤4：使用测试样本集测试模型的准确性，保证神经网络模型拟合良好，不存在欠拟合和过拟合的现象，准确率需达到90％以上。

进一步的，四个维度的河流基础数据处理过程如下：

(1)基于河流基础数据，计算河流复氧速率、弯曲度和连通度，

(1.1)复氧速率计算方法：对于水深较深、流速缓慢的河流，使用公式(5)(7)计算；对于水深较浅、流速较大(靠实验和经验确定)的河流，使用公式(6)(7)计算，

式中，k2为复氧系数；d为氧在水体中的分子扩散系数；u为平均流速；h为河流水深；j为水面坡降；κ为卡门常数，一般取0.4；g为重力加速度；

式中，o为溶解氧浓度；os为饱和溶解氧浓度，t为时间；

使用公式(8)计算河流弯曲度：

ie＝s/l(8)

式中，ie为河流弯曲度；s为河流中泓线长度；l为河流起止断面距离；

(1.2)河流连通度计算方法：水系的环通度α使用公式(9)计算；水系节点率β使用公式(10)计算；水系网络连通度γ使用公式(11)计算，

式中，α为水系的环通度；m为城市连接的廊道数量；v为水系节点个数；β为水系节点率；mmax为最大的廊道数量；

(2)层次分析法结合熵权法，对水质指标和水动力指标降维；

(2.1)层次分析法得到主观赋权的权重值：

2.1.a.建立层次结构模型，根据收集的水质和水动力参数，分目标层、准则层和方案层建立层次结构模型；

2.1.b.建立判断矩阵，根据步骤a建立的层次结构模型构建成对比较矩阵(判断矩阵)，包括分别基于目标层、准则层和方案层的判断矩阵，并计算特征向量和特征值；

2.1.c.进行层次单排序及其一次性检验，分别计算准则层对目标层和方案层对准则层的权重排序，分别做一次性检验；

2.1.d.进行层次总排序及其一次性检验，计算方案层对目标的权重排序及其一致性检验；

(2.2)熵权法得到客观赋权的权重值：

2.2.a.构建原始数据矩阵x＝(xij)m×n，并归一化，

2.2.b.使用公式(12)计算熵值

式中，ej为j指标的熵值；m2为曝气河流样本数量；n为指标数量；pij为xij归一化后的矩阵；

2.2.c.使用公式(13)计算权重

式中，jj为j指标的权重；

2.2.d.使用公式(14)归一化处理

式中，βj为j指标的客观权重值；

利用公式(15)计算综合权重值

式中，w为由乘法归一组合赋权法得到的权重值；αj为主观赋权得到的权重值；βj为客观赋权得到的权重值；

(3)将生物数据划分为自养生物和异养生物，分别计算生物完整性指数；计算方法为：

3.a.选择受损点和参照点，选择生态修复前的数据为受损点，生态修复后的数据为参照点；

3.b.依据敏感性分析结果剔除参数，对生物参数做敏感性分析，其中iq小于2的参数，不再做进一步分析，对于iq值大于或等于2的参数，保留，并进入步骤3.c；

3.c.对剔除共线性参数，敏感性分析筛选后的参数进一步做pearson相关分析和共线性

分析，按照|r|>0.75或vif≥20的标准，剔除共线性的参数；

式中，r为相关系数；vif为方差膨胀因子；r²为决定系数；m2为曝气河流样本数量；xi,yi为成对的样本；

3.d.按照三分法，首先计算构成生物完整性指数值(ibi值)的参数在参照点的统计分布，拟定其评价指标的评分标准，据此将每个样点的参数的评价值实测值分别进行评分，然后将选出的参数得分进行累加，最后得到每个样点的ibi总分；

3.e.按照比值法，首先计算生物参数在全部样点中的95％或5％分位数的值；最后将选出的参数的分值进行累加，即得出各样点的ibi总分值。

进一步的，所述步骤二所需的曝气量，即维持河流最佳需氧量的计算方法为：

步骤(1)：构建河流食物网模型，以生物与营养物质之间的相互作用、生物间相互作用为基础，构建河流食物网模型；

步骤(2)：基于动力学参数和实际收集的数据，模拟河流生态系统的生物量变化和营养物质变化，通过比对实际数据和模拟数据，率定动力学参数，使河流食物网模型的准确度符合需求；

步骤(3)：对河流食物网模型的初始输入值做敏感性分析，找到控制河流生态系统的关键变量；

步骤(4)：以当前溶解氧浓度为基准，以当前温度下的饱和溶解氧浓度为上限，以0.2mg/l为间隔，生成溶解氧序列；将生成的溶解氧序列依次输入河流食物网模型，其余初始值使用当前时间的在线监测值，动力学参数使用经率定的参数；根据步骤(3)敏感性分析识别出的关键变量，以关键变量最优为目标，得到河流的最佳需氧量。

进一步的，所述率定动力学参数的过程是：先使用文献或实验测得的动力学参数，输入模型进行模拟，得到预测值与实际值比较，|预测值-实际值|/实际值可以表示模型的准确度。根据模型的需求不同，选取不同的准确度阈值。(例如要求准确度为80％，则根据准确度低于80％的预测值，修改该指标对应的动力学参数，直至所有指标的预测值达到80％。)

进一步的，找到控制河流生态系统的关键变量的具体过程为：根据公式(18)计算不同变量的标准局部敏感系数

式中，si,j为标准局部敏感系数；αi为模型参数相对变化量；vj为模型输出变量的相对变化量；为参数默认值改变1％；

标准局部敏感系数si,j大于1表示变量敏感，即关键变量。

本发明的有益效果是：

1、能根据河流现状，科学设定河流曝气修复的目标和策略，准确判断河流是否需要曝气，避免出现停止曝气后，河流水质出现“反弹”。

2、能精细化控制河流修复的整个曝气过程，通过计算最佳需氧量，在保证曝气效果的前提下，降低曝气设备的使用能耗，达到节约能源，降低运行成本的目的。

3、本发明通过神经网络模型建模和预训练处理，在应用与河流时，只需采集河道的思维数据，并输入神经网络模型，便可计算出河流的最佳需氧量以及曝气量，做到科学治理河道水体。

附图说明

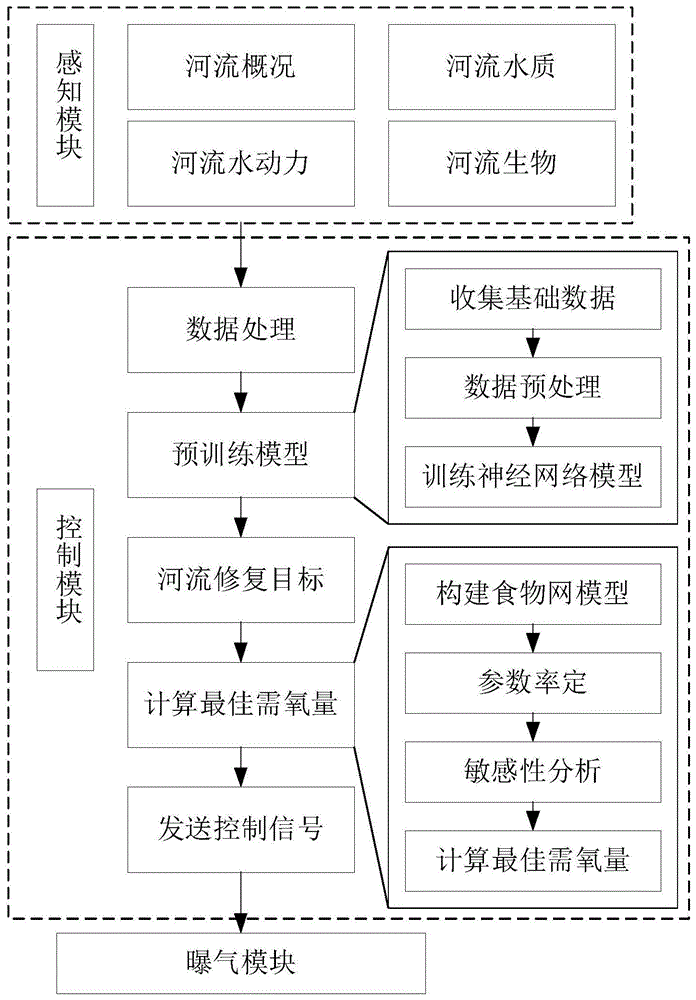
图1是本发明的控制流程图，

图2是神经网络平均平方误差图，

图3是动力学模型状态变量结构图，

图4是本发明数据流向概图，

图5是本发明曝气目标模型(基于神经网络算法)的建模过程图，

图6是本发明曝气目标模型模型使用图，

图7是本发明最佳曝气量模型的运算过程概图。

具体实施方式

现在结合附图对本发明作进一步详细的说明。这些附图均为简化的示意图，仅以示意方式说明本发明的基本结构，因此其仅显示与本发明有关的构成。

如图1所示，本发明系统包括三大板块，分别为感知模块、控制模块、曝气模块。

感知模块主要是指用于采集河流基础数据的各种设备，采集的数据为：河流概况、河流水质、河流水动力和河流生物四个维度的河流基础数据，包括理化指标监测、生物监测和河流耗氧速率在线监测，四个维度的数据，有两个用途，分别是计算最佳曝气量和确定能否停止曝气。采集的数据输入控制模块，数据输入方式可以是人机交互界面输入、传感器中的任意一种或多种。

其中生物监测的监测方式可以是在线监测、现场实测、实验室监测中的任意一种或多种。监测指标可以是微生物、原生动物、后生动物、鱼类、藻类、浮游植物、沉水植物中的一种或多种。

控制模块包括建模、预处理、训练，形成稳定的神经网络模型，然后使用神经网络模型，处理河流的四个维度数据，得出河流的最佳需氧量和曝气量。

曝气模块可选用现有的曝气设备，或者可选专利号为201910914913.7公开的一种用于河流修复的曝气系统，对河流进行曝气，控制模块与其控制连接，控制其曝气流速、时间、曝气量等参数。

下面介绍本发明系统的控制方法，包括以下步骤：

步骤一：获取河流概况、河流水质、河流水动力和河流生物四个维度的数据，通过人机交互的方式输入控制模块，控制模块对输入数据经过预处理后，输入神经网络模型，计算出通过曝气修复河流的目标值；

步骤二：启动曝气模块，感知模块和控制模块同步开始工作，根据曝气模块启动前输入控制模块的数据，以及感知模块实时监测的数据，每隔六小时计算一次河流最佳曝气量，按公式(1)(2)计算曝气量，向曝气模块发送控制信号，控制曝气的强度和时间；根据感知模块传输给控制模块的数据，实时监控河流曝气情况，维持河流的溶解氧浓度在预期水平；

e(k)＝domeasure(k)-doset/default(k)(2)

式中，q(k)表示曝气量，kp表示e(k)项的系数，ki表示项的系数，kd表示[e(k)-e(k-1)]项的系数，k表示k时刻，e(k)表示k时刻测量值与设置/预设溶解氧浓度值的偏差，e(k-1)表示k-1时刻测量值与设置/预设值的偏差，domeasure(k)表示测量得到的k时刻溶解氧浓度，doset/default(k)表示k时刻曝气器控制模块溶解氧的输入值或预设值；

步骤三：循环步骤二，直至感知模块监测的河流的现状达到神经网络模型得到的曝气修复河流的目标值，停止曝气并通知管理人员。

其中，建立神经网络模型及其训练过程如下：

步骤1：收集基础数据，选取有代表性的河流，收集包括河流曝气修复前后常规理化指标、生物指标，以及河流宽度、深度、功能、周围土地利用类型、污染源情况，至少80组数据；

步骤2：数据预处理(该数据预处理过程与下面模型使用过程中的数据预处理是一致的。建立神经网络模型时，首先对数据预处理，使用神经网络模型测试数据时，也要首先进行同样的数据预处理，剔除明显异常数据。)，首先剔除明显异常和错误的数据，然后基于公式(3)做共线性分析，剔除共线性高的数据，再用排序算法做进一步降维，将输入指标降低到10个以内；最后，将处理好的数据划分为训练样本集和测试样本集；(随机按7：3划分训练样本集和测试样本集)

式中，r²为决定系数；vif≥20剔除，vif＜20保留；

步骤3：训练神经网络模型，将预处理后的结果作为输入层，将溶解氧浓度、氨氮浓度、化学需氧量、河流耗氧速率、自养生物占比作为输出层，输入层神经元数量与预处理后的指标个数相同，输出层神经元数量为5个；隐含层数量与神经元个数根据神经网络模型的质量进行调整，默认为两层；完成建模后，训练神经网络模型，根据输出结果，评估模型的损失函数，按公式(4)计算平均平方误差mse表示神经网络模型的损失，直至图谱表现为水平直线，判定为符合要求；

h(xⁱ)代表预测的第i个值，yⁱ代表实际的第i个值；m1为测试集样本数量；

步骤4：使用测试样本集测试模型的准确性，保证神经网络模型拟合良好，不存在欠拟合和过拟合的现象，准确率需达到90％以上(参见图2)。

上述神经网络模型建立以及训练后，可采集待曝气河流的基本数据，输入上述建模以及训练后的模型中，进行如下步骤，即运行神经网络模型：

(1)基于河流基础数据，计算河流复氧速率、弯曲度和连通度，

(1.1)复氧速率计算方法：对于水深较深、流速缓慢的河流，使用公式(5)(7)计算；对于水深较浅、流速较大(靠实验和经验确定)的河流，使用公式(6)(7)计算，

式中，k2为复氧系数；d为氧在水体中的分子扩散系数；u为平均流速；h为河流水深；j为水面坡降；κ为卡门常数，一般取0.4；g为重力加速度；

式中，o为溶解氧浓度；os为饱和溶解氧浓度，t为时间；

使用公式(8)计算河流弯曲度：

ie＝s/l(8)

式中，ie为河流弯曲度；s为河流中泓线长度；l为河流起止断面距离；

(1.2)河流连通度计算方法：水系的环通度α使用公式(9)计算；水系节点率β使用公式(10)计算；水系网络连通度γ使用公式(11)计算，

式中，α为水系的环通度；m为城市连接的廊道数量；v为水系节点个数；β为水系节点率；mmax为最大的廊道数量；

(2)层次分析法结合熵权法，对水质指标和水动力指标降维；

(2.1)层次分析法得到主观赋权的权重值：

2.1.a.建立层次结构模型，根据收集的水质和水动力参数，分目标层、准则层和方案层建立层次结构模型；

2.1.b.建立判断矩阵，根据步骤a建立的层次结构模型构建成对比较矩阵(判断矩阵)，包括分别基于目标层、准则层和方案层的判断矩阵，并计算特征向量和特征值；

2.1.c.进行层次单排序及其一次性检验，分别计算准则层对目标层和方案层对准则层的权重排序，分别做一次性检验；

2.1.d.进行层次总排序及其一次性检验，计算方案层对目标的权重排序及其一致性检验；

(2.2)熵权法得到客观赋权的权重值：

2.2.a.构建原始数据矩阵x＝(xij)m×n，并归一化，

2.2.b.使用公式(12)计算熵值

式中，ej为j指标的熵值；m2为曝气河流样本数量；n为指标数量；pij为xij归一化后的矩阵；

2.2.c.使用公式(13)计算权重

式中，uj为j指标的权重；

2.2.d.使用公式(14)归一化处理

式中，βj为j指标的客观权重值；

利用公式(15)计算综合权重值

式中，w为由乘法归一组合赋权法得到的权重值；αj为主观赋权得到的权重值；βj为客观赋权得到的权重值；

(3)将生物数据划分为自养生物和异养生物，分别计算生物完整性指数；计算方法为：

3.a.选择受损点和参照点，选择生态修复前的数据为受损点，生态修复后的数据为参照点；

3.b.依据敏感性分析结果剔除参数，对生物参数做敏感性分析，其中iq小于2的参数，不再做进一步分析，对于iq值大于或等于2的参数，保留，并进入步骤3.c；

3.c.对剔除共线性参数，敏感性分析筛选后的参数进一步做pearson相关分析和共线性

分析，按照|r|>0.75或vif≥20的标准，剔除共线性的参数；

式中，r为相关系数；vif为方差膨胀因子；r²为决定系数；m2为曝气河流样本数量；xi,yi为成对的样本；

3.d.按照三分法，首先计算构成生物完整性指数值(ibi值)的参数在参照点的统计分布，拟定其评价指标的评分标准，据此将每个样点的参数的评价值实测值分别进行评分，然后将选出的参数得分进行累加，最后得到每个样点的ibi总分；

3.e.按照比值法，首先计算生物参数在全部样点中的95％或5％分位数的值；最后将选出的参数的分值进行累加，即得出各样点的ibi总分值。

(4)将上述计算结果输入训练好的神经网络模型，即可得到曝气修复河流的目标值。

步骤二所需的曝气量，即维持河流最佳需氧量的计算方法为：

步骤(1)：构建河流食物网模型，以生物与营养物质之间的相互作用、生物间相互作用为基础，构建河流食物网模型(参见图3)；

步骤(2)：基于动力学参数和实际收集的数据，模拟河流生态系统的生物量变化和营养物质变化，通过比对实际数据和模拟数据，率定动力学参数，使河流食物网模型的准确度符合需求；

率定动力学参数的过程是：先使用文献或实验测得的动力学参数，输入模型进行模拟，得到预测值与实际值比较，|预测值-实际值|/实际值可以表示模型的准确度。根据模型的需求不同，选取不同的准确度阈值。(例如要求准确度为80％，则根据准确度低于80％的预测值，修改该指标对应的动力学参数，直至所有指标的预测值达到80％。)

步骤(3)：对河流食物网模型的初始输入值做敏感性分析，找到控制河流生态系统的关键变量；

找到控制河流生态系统的关键变量的具体过程为：根据公式(18)计算不同变量的标准局部敏感系数

式中，si,j为标准局部敏感系数；αi为模型参数相对变化量；vj为模型输出变量的相对变化量；为参数默认值改变1％；

标准局部敏感系数si,j大于1表示变量敏感，即关键变量。

步骤(4)：以当前溶解氧浓度为基准，以当前温度下的饱和溶解氧浓度为上限，以0.2mg/l为间隔，生成溶解氧序列；将生成的溶解氧序列依次输入河流食物网模型，其余初始值使用当前时间的在线监测值，动力学参数使用经率定的参数；根据步骤(3)敏感性分析识别出的关键变量，以关键变量最优为目标，得到河流的最佳需氧量。

下面具体阐述河流最佳需氧量(曝气量)与曝气修复河流的目标值的关系：

参见图4，感知模块获取数据，传输给控制模块，控制模块将数据转化成控制信号，发送给曝气模块；控制信号有两种，一种是控制是否曝气，此时，需要曝气目标模型做计算，另一种是调节曝气的强弱，此时，需要最佳曝气量模型做计算。

曝气目标模型是基于神经网络算法的，包括训练模型和使用模型，训练模型仅训练一次即可，训练完成后，可一直使用；训练模型和使用模型使用的数据需要做相同的预处理(降维、去共线性、特征工程等)。模型训练过程如图5所示，其中，步骤8对模型准确度评估后，符合要求则结束；否则，重复步骤3，直至模型准确度符合要求。模型的使用过程如图6所示，在已训练模型的基础上，输入数据，预处理，经过神经网络模型运算，输出曝气修复河流的目标值。

最佳曝气量模型即上述步骤二的详细算法，可参见图7，通过输入数据，构建食物网模型，识别关键变量，计算最佳曝气量。

以上述依据本发明的理想实施例为启示，通过上述的说明内容，相关工作人员完全可以在不偏离本项发明技术思想的范围内，进行多样的变更以及修改。本项发明的技术性范围并不局限于说明书上的内容，必须要根据权利要求范围来确定其技术性范围。