一种砂带磨削螺杆曲面表面粗糙度的预测方法

本发明涉及砂带磨削加工领域，具体涉及一种砂带磨削螺杆曲面表面粗糙度预测方法。

背景技术：

多头螺杆转子是钻具、螺杆泵等器械的重要组成之一，应用在石油、化工、军工、轻工等行业。其表面粗糙度影响着螺杆在作业时的稳定性、耐磨性等等。近15年来螺杆在我国空压机，冷冻机，工业泵，塑料机械中应用越来越广泛，行业内对螺杆表面质量的要求日益增高，所以需要一种表面粗糙度预测算法，能够根据给定实验数据训练之后，得到不同磨削参数下的表面粗糙度数值。

现有的bp神经网络预测中存在的局部极小化、收敛速度慢、出现过拟合等现象。目前，现有砂带磨削螺杆曲面表面粗糙度预测方法预测速度慢，准确性差，不足以利用来预测螺杆表面粗糙度数值，所以需要提出一种新的算法来进行预测。

技术实现要素：

发明目的：

本发明提出一种砂带磨削螺杆曲面表面粗糙度预测方法，其目的在于提出一种可以使螺杆工件表面粗糙度在给定条件下快速预测出的方法，提高预测表面粗糙度准确性。

技术方案：

本发明涉及一种砂带磨削螺杆曲面表面粗糙度的预测方法，获取螺杆砂带磨削加工参数中对表面粗糙度产生影响的参数，确定实验数据；将数据输入为矩阵形式，样本归一化之后的数据分别作为基于麻雀搜索方法优化神经网络算法的输入p与输出t；确定网格结构；通过麻雀觅食优化方法获得优化后的bp神经网络的权值与阈值；利用优化后bp神经网络的权值与阈值代入bp神经网络进行训练；根据训练结果最终预测出不同工况下工件的表面粗糙度数值。本方法使螺杆工件表面粗糙度在给定条件下快速预测，提高预测表面粗糙度准确性。

麻雀觅食优化方法的步骤为：

s1将个实验数据根据麻雀觅食、躲避天敌的特点定义为三种可能的个体：发现者、跟随者和警戒者；

s2根据个体数量模型计算出初始化种群个体的数量j，并设定迭代次数maxgen与发现者比例p_percent；

s3根据s2中设定的发现者比例、种群数量，产生s个发现者，将bp神经网络的初始权值与阈值作为麻雀的初始群体x，得到一组表面粗糙度预测值，以实测值与预测值的误差函数作为适应度函数fx；

s4根据麻雀搜索方法中麻雀的觅食规则，发现者根据发现者更新位置变更模型变更坐标；跟随者根据跟随者更新位置变更模型变更坐标；警戒者根据警戒者更新位置变更模型变更坐标；当误差值小于给定误差时，终止更新迭代，此时麻雀群体x即为优化后的bp神经网络的权值与阈值。

步骤2)中归一化模型为：

式中，y为归一化之后的数据，x为当前数据个体，xmin为给定数据中数值最小的个体，xmax为给定数据个体中数值最大的个体。

步骤3)中隐层神经元模型为：

式中k为隐层神经元个数，m为输入层神经元个数，n为输出层神经元个数，α是常数，取值[1,10]。

s2中个体数量模型为：

j＝k(m+n)+n+k

式中k为隐层神经元个数，m为输入层神经元个数，n为输出层神经元个数，α是常数，取值[1,10]。

发现者是群体中发现适应度f最小的坐标位置的个体；跟随者是跟随发现者抢夺适应度f最小的坐标位置的个体，当抢夺失败之后会去寻求新的适应度坐标，若发现适应度f最小的坐标位置则跟随者变成发现者；警戒者是群体中随机产生的个体，当群体x朝着误差越来越大的方向迭代时，警戒者阻止群体x越界，使群体x朝着误差小的方向收拢。

s3中麻雀群体x为：

其中，d表示待优化问题的维数，n是麻雀数量；

适应度函数fx为：

其中，f表示适应度值。

s4中发现者更新位置变更模型：

式中，t为此刻迭代次数；j＝1,2,3,...,d；itermax表示最大迭代次数；表示第i个麻雀在第j维中的位置属性信息；α∈(0,1]是一个随机的常数；r2(r2∈(0,1])与st(st∈(0.5,1])分别代表的是预警值与安全值；q是一个服从正态分布的随机数；l是一个d维的列矩阵，其中每个元素全部等于1。

s4中跟随者更新位置变更模型：

其中，xp是此时发现者的最优位置；xworst为全局最差的位置；a是一个类似于l的d维的列矩阵，每个元素随机取值到1或-1，并且a⁺＝a^t(aa^t)^-1。

s4中警戒者更新位置变更模型：

其中，为当前的全局最优值；β为步长参数；是服从均值为0，方差为1的正态分布的随机数；k∈[-1,1]也是一个随机数；fi是当前个体的适应度值；fg与fw分别代表当前全局的最佳适应度值与最差适应度值；ε是一个常数。

优点效果：

本方法改善了bp神经网络预测中存在的局部极小化、收敛速度慢、出现过拟合等现象，并可以快速在给定条件下预测出工件表面粗糙度。通过对比三组方法训练预测数据平均误差可以得出预测性能的准确度高低，ssa-ap所达到的平均误差要低于gabp与传统bp，准确性更强。

附图说明

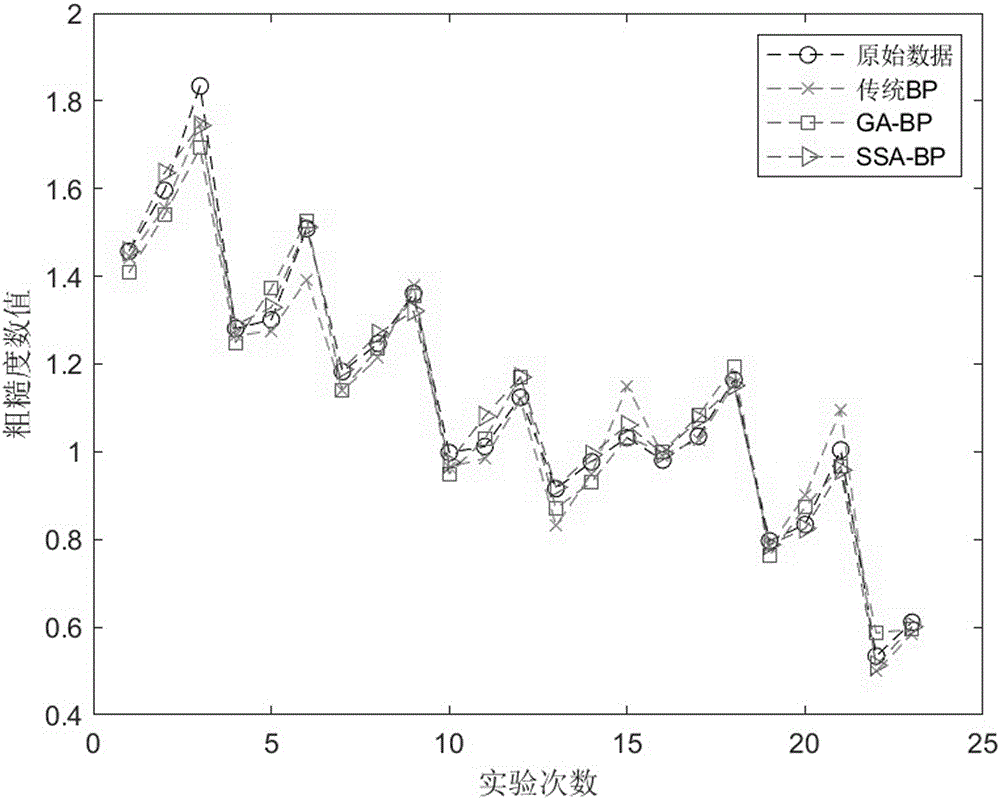
图1为训练结果对比图；

图2为预测结果对比图；

图3为ssa-bp全过程流程图。

具体实施方式

以下结合说明书附图更详细的说明本发明。

本发明为预测磨削加工之后的螺杆表面粗糙度，意义在于通过表面质量预测研究，预判出磨削加工时不同加工参数组合所对应的表面粗糙度值，从而达到合理选择磨削加工参数，获得理想加工表面质量的目的。

为改善bp神经网络预测中存在的局部极小化、收敛速度慢、出现过拟合等现象，提出了基于麻雀搜索方法(ssa)优化bp神经网络的算法(ssa-bp)，对bp神经网络的初始权值、阈值进行优化，实现多头螺杆同步磨削装置磨削后工件表面粗糙度的精确预测。

麻雀搜索方法(ssa)中麻雀的觅食规则：

1)发现者是群体中需要寻找具有丰富食物的区间的个体，这些发现者通常具有比较高的能量储备值，为所有的跟随者以及警戒者提供觅食的场所区域方向。麻雀个体的能量储备值对应麻雀个体的适应度值的好坏。

2)在觅食过程中，一旦警戒者发现了天敌，警戒者个体会开始发出鸣叫声作为报警信号。且当安全值小于所发出的报警值时，发现者就会将跟随者带到另一个安全区域进行觅食。

3)所有个体的身份是会随着迭代而改变的。只要麻雀个体搜寻到了更好的食物来源，那么这个个体就可以称之为发现者，但是发现者和跟随者之间的比值是恒定不变的，也就是说每有一个跟随者变成发现者，那么就会存在一个发现者变成跟随者。

4)跟随者的能量是偏低的，总是低于发现者的能量储备，而能量储备越低，在整个种群的觅食条件就越差，这样就导致一些能量储备极低的跟随者会脱离此时的发现者，飞往其他地方觅食，获得更多的能量储备。

5)在发现者觅食的过程中，跟随者总是能寻找到可以提供最好食物的发现者。然后在该发现者周围进行觅食，进而一些跟随者可能会为了增加自己的能量储备值，就会不断的监控发现者而去抢夺食物。

6)当警戒者发现危险时，远离安全区的麻雀会向安全区迅速靠拢，以便躲避天敌的追捕，靠近其他的麻雀个体。

本发明方法结合麻雀搜索方法(ssa)的原理为：首先将所有的网络权值与阈值定义成麻雀群体x，然后计算他们每个麻雀个体的适应度值f(误差值)，将误差值较小的个体定义为发现者个体这些发现者个体会继续去寻找食物(数据坐标)来获得更小的误差值，(获得食物就会使误差降低)；而跟随者是去抢夺发现者的食物来获得更低的误差值，而当跟随者抢夺成功时会降低误差值；当发现者抢夺失败时跟随者会变成发现者重新发现食物，根据此规则更新跟随者而警戒者是随机产生的，警戒者个体的作用是当群体朝着误差越来越大的方向迭代时，阻止群体越界，朝着误差小的方向收拢，根据此规则更新警戒者当迭代次数达到给定迭代终止次数之后，迭代终止，此时麻雀群体x即为更新之后的最终神经网络的权值与阈值。

如图3所示，一种砂带磨削螺杆曲面表面粗糙度预测方法，步骤为：

1)获取螺杆砂带磨削加工参数中对表面粗糙度产生影响的参数，根据选定的参数，确定实验数据；影响螺杆砂带磨削的加工参数有对表面粗糙度产生影响的因素有工件速度vg、砂带速度vs、砂带张紧力fs、磨削压力fm等。

2)将数据输入为矩阵形式，并且归一化模型对其进行归一化，采用线性转换；归一化模型为：

式中，y为归一化之后的数据，x为当前数据个体，xmin为给定数据中数值最小的个体，xmax为给定数据个体中数值最大的个体。

样本归一化之后的数据分别作为ssa-bp的输入p与输出t。

3)确定网格结构

输入p维数为n，确定输入层单元个数为n(n为正整数，根据实验加工的参数确定，比如实验有5个输入参数，则n＝5)，根据隐层神经元模型计算出隐层神经元个数。

隐层神经元模型为：

式中k为隐层神经元个数，m为输入层神经元个数，n为输出层神经元个数，α是常数，取值[1,10]；

4)步骤1)中，每个实验数据根据麻雀觅食、躲避天敌的特点定义为三种可能的个体：发现者、跟随者和警戒者；

发现者、跟随者和警戒者的定义：

发现者是群体中发现适应度f最小的坐标位置的个体；发现者会发现食物，即发现适应度f(误差)最小的位置坐标。

跟随者是跟随发现者抢夺适应度f最小的坐标位置的个体，当抢夺失败(抢夺成功与否是随机的，式中表达为若加入者的下角标i值是否大于n/2；大于则抢夺失败，需要去探索新的食物成为发现者，小于则成功，获得该发现者的食物。)之后会去寻求新的适应度坐标，若发现适应度f最小的坐标位置则跟随者变成发现者；跟随者会去抢夺发现者发现的位置坐标，抢夺成功跟随者将获得这些坐标，成为新的发现者，抢夺失败则要去发现新的食物坐标；

警戒者是群体中随机产生的个体，当群体x朝着误差越来越大的方向迭代时，警戒者阻止群体x越界，使群体x朝着误差小的方向收拢，根据此规则更新警戒者警戒者会根据设定的安全值在安全区域内警戒，一旦探索的位置坐标超出这些安全值，即发现天敌时会产生警报值，天敌即探索的方向出现了偏差，朝着误差越来越大的方向进行探索，此时警戒者就会发出警报让群体撤离这个位置，所有个体撤离到安全区域。

5)根据个体数量模型计算出初始化种群个体的数量j，并设定迭代次数maxgen与发现者比例p_percent。

个体数量模型为：

j＝k(m+n)+n+k

式中k为隐层神经元个数，m为输入层神经元个数，n为输出层神经元个数，α是常数，取值[1,10]；

6)根据步骤4)中设定的发现者比例、种群数量，产生s(s为正整数，占比是后续实例中具体设定的，后续实例中取s的占比为20％，初始群体个数为36，s＝36*0.2，取整之后s＝7)个发现者，将随机产生的种群个体赋值给bp神经网络，将bp神经网络的初始权值与阈值作为麻雀的初始群体x，得到一组表面粗糙度预测值，以实测值与预测值的误差函数作为适应度函数fx(即食物)；每个个体需要根据觅食原则进行寻优，此时麻雀的适应度函数为fx(fx即为个体误差值大小)；适应度函数fx用来评价权值与阈值的优劣程度；

由n只麻雀组成的群体x，可表示为如下形式：

d表示待优化问题的维数，n则是麻雀数量，那么，所有麻雀个体的适应度值可以用适应度函数式来表示：

在ssa当中，具有较高能量储备值(误差值较小)的发现者个体会在觅食过程中优先获得食物。除此之外，由于发现者需要为整个群体搜寻食物并且为跟随者提供觅食的方向，所以发现者可以拥有比其他个体更大的觅食搜寻范围。

7)每个个体需要根据麻雀搜索方法(ssa)中麻雀的觅食规则进行寻优，进行位置更新。直至误差(即适应度f)小于给定误差时，生成新的麻雀位置矩阵x，将矩阵中的所有个体赋值给bp神经网络的权值与阈值。若误差(即适应度f)大于给定误差或迭代次数小于给定迭代次数时，则需要继续迭代跟新。

根据麻雀搜索方法(ssa)中麻雀的觅食规则1)与2)，每次迭代，发现者的位置根据发现者更新位置变更模型进行更新：

发现者更新位置变更模型为：

式中，t为此刻迭代次数；j＝1,2,3,...,d；itermax表示最大迭代次数；表示第i个麻雀在第j维中的位置属性信息。α∈(0,1]是一个随机的常数；r2(r2∈(0,1])与st(st∈(0.5,1])分别代表的是预警值与安全值；q是一个服从正态分布的随机数；l是一个d维的列矩阵，其中每个元素全部等于1。

当发现者更新位置变更模型中的r2＜st时，此时意味着觅食环境的周围并没有天敌捕食者，发现者可以根据其搜索半径进行广泛的搜索。如果r2＞st时，此时表示种群中的一些麻雀已经发现了捕食者，并且向其他的个体发出了警报，预警值大于了安全值，此时所有的麻雀个体需要迅速飞往其他安全区域进行觅食。

对于跟随者个体，它们所需要执行的麻雀搜索方法(ssa)中麻雀的觅食规则是3)与4)。在寻找食物时，这些跟随者会始终监视着发现者，一旦跟随者个体察觉到了发现者已经搜寻到了更好的食物，跟随者个体就会立刻离开现有的区域而去跟发现者争夺食物。如果跟随者赢了，它们就可以立刻获得发现者的食物，否则还需要继续执行麻雀搜索方法(ssa)中麻雀的觅食规则4)。对于跟随者的执行描述如跟随者更新位置变更模型所示。

跟随者更新位置变更模型为：

其中，xp是此时发现者的最优位置；xworst为全局最差的位置；a是一个类似于l的d维的列矩阵，每个元素随机取值到1或-1，并且a⁺＝a^t(aa^t)^-1。当此时表示第i个跟随者适应度较低，没有获得食物来源，并且处于十分饥饿的状态，这时就需要执行规则4)，前往其他地方觅食以获得能量。在种群中，假设警戒者个体占群体数量的10％到20％，这些警戒者个体初始位置是在种群当时随机选取的，那么根据麻雀搜索方法(ssa)中麻雀的觅食规则5)，其表达式可以为警戒者更新位置变更模型。

警戒者更新位置变更模型为：

式中，为当前的全局最优值；β为步长参数；是服从均值为0，方差为1的正态分布的随机数；k∈[-1,1]也是一个随机数；fi是当前个体的适应度值；fg与fw分别代表当前全局的最佳适应度值与最差适应度值；ε是一个常数，为了避免分母会出现等于0的情况。

终止条件为设定的迭代次数；当满足终止条件时，退出得到优化过的初始神经网络权值与阈值。若未满足条件，则需要重复步骤6)。

8)利用优化后bp神经网络的权值与阈值代入bp神经网络进行训练；根据训练结果最终预测出不同工况下工件的表面粗糙度数值。

实施例1

根据螺杆同步磨削装置为依托，实施螺杆砂带磨削表面预测的实验任务。影响螺杆砂带磨削的加工参数有对表面粗糙度产生影响的因素有工件速度vg、砂带速度vs、砂带张紧力fs、磨削压力fm等。

(1)数据初始化，将实验得到的数据整理如表1所示:

表1实验数据

(2)输入p维数为5，所以确定输入层单元个数为5；输入t为一维，所以确定输出层单元格数为1。计算出隐层神经元个数为5，初始化种群个体的数量j＝36，设定迭代次数maxgen＝100，设定发现者比例p_percent＝0.2。

(3)根据设定的参数与实验数据，利用麻雀搜索算法优化bp神经网络，并利用优化过的网络对其进行训练，将得到的训练结果与经典bp神经网络和ga-bp神经网络对比，对比如图1所示，预测误差具体值如表2所示。

表2三种方法预测结果误差对比

通过对比三组方法训练预测数据平均误差可以得出预测性能的准确度高低，ssa-ap所达到的平均误差要低于gabp与传统bp，准确性更强。

(4)将实验数据的后4组数据作为预测模型的验证，以对应的参数作为输入，并根据ssa-bp预测模型进行预测，与原实验数据进行对比。对比图如图2所示。计算出三种方法预测的数值对比实验数据，平均误差最小的为ssa-bp的7.15％，其次是ga-bp，误差值为13.63％，最后是经典bp网络的误差值为15.48％。

综上，本方法可以使螺杆工件表面粗糙度在给定条件下进行快速预测，且提高预测表面粗糙度准确性。