数据驱动的电动汽车充电需求的时空价格弹性估计方法

本发明属于电动汽车需求响应领域，特别涉及一种数据驱动的电动汽车充电需求的时空价格弹性估计方法。

背景技术：

随着技术的进步和政策的推动，电动汽车的发展很快。对在城市内提供运行服务的电动汽车来说(如出租车、网约车等)，很大一部分充电需求在公共快速充电站得到满足。由于电动汽车的负荷十分灵活，电动汽车充电需求可以在价格驱动下，从一个时段转移到另一个时段，从一个充电站转移到另一充电站。也就是，公共充电站的定价能对充电需求在时空上的分布产生影响。为了衡量充电需求对价格的响应大小，就需要量化充电需求的价格弹性，从而使得电网公司通过对电动汽车充电负荷引导来降低配电网容量压力，实现电力资源的合理分配。

电动汽车在有序充电的情况下，可以成为电网的一种资产，而不仅仅是电网的负荷。从充电服务商角度来看，充电服务商所拥有的足够数量的电动汽车可以为电网提供服务，如提供给调峰调频资源和服务等。从电网角度来看，对充电需求的价格引导，对电网是有益的。价格信号是对于不接受电网调度命令的车辆进行调控的一种手段，由于不能直接控制电动汽车负荷，需要将控制信号转化为价格信号，在激励相容的价格策略下，间接调控充电需求。

传统中，估计充电需求的价格弹性的方法是一个实验性的方法，通过修改充电价格，观察充电需求的变化，然后求出充电需求的价格弹性。然而实验性的方法实施较为困难，现阶段的研究还没有直接从充电数据中评估充电需求的价格弹性方法。专利cn202011014332.7一种考虑需求响应和电动汽车的联合微电网运行策略和cn201910317334.4一种配电网电动汽车时空充放电电价制定方法，两者均运用了电动汽车充电需求的价格弹性矩阵来进行系统运行策略和充电价格策略的优化。然而在这两个专利中，均没有涉及对充电需求的价格弹性矩阵具体获取方法。

技术实现要素：

本发明的目的是为克服已有技术的不足之处，提出一种数据驱动的电动汽车充电需求的时空价格弹性估计方法。本发明可以应用在电动汽车充电领域，根据本发明得到的充电需求的价格弹性结果，电网公司能够更有效掌握电动汽车用户对充电价格的响应，从而合理制定分时、分区域电价，来减少电网容量的压力。

本发明提出一种数据驱动的电动汽车充电需求的时空价格弹性估计方法，其特征在于，该方法首先获取每个区域在研究时间内的充电历史数据，对历史数据进行归一化处理，得到各区域每日每时段归一化后的充电需求和充电价格并组成训练集；然后建立一个条件随机场模型，其中将充电价格作显式随机变量，充电需求作为隐式随机变量，确定条件随机场模型的拓扑结构及条件随机场模型的特征函数；利用训练集对条件随机场模型进行训练，得到训练完毕的条件随机场模型；利用训练完毕的条件随机场模型，计算任一区域任一时段充电价格对各区域任一时段充电需求的影响即得到时空价格弹性。该方法包括以下步骤：

1)划分研究区域，获取每个区域在研究时间内的充电历史数据，对历史数据进行归一化处理，得到各区域每日每时段归一化后的充电需求和充电价格并组成训练集；具体步骤如下：

1-1)将研究的地区划分为若干块大小一样的区域，记划分成的区域集合为该集合中共包含k个区域；

将一天的时间划分为t个时段，记划分为的时段集合为

1-2)获取步骤1)划分的每一块区域中的所有充电站在研究时间内的充电历史数据，得到在研究时间内的每一个区域的每日平均充电量各区域充电站数量ni；并且得到每一个区域在研究时间内每日每时段总充电量研究时间内每日每时段加权度电充电价格研究时间内每时段日平均的加权度电充电价格研究时间内每时段日平均充电量其中下标表示第i个区域，上标表示第t个时段，τ表示第τ天；

1-3)对步骤1-2)获取的每一区域的和分别进行归一化，得到归一化后的各区域每日每时段总充电量即归一化后的充电需求，以及归一化的各区域加权度电充电价格即归一化后的的充电价格，归一化公式分别如下：

1-4)将归一化后的充电价格和充电需求组成训练集其中小括号代表一个区域在一个时段的充电需求和充电价格对，中括号表示第τ天中所有区域在所有时段的充电需求和充电价格对数据；

2)建立条件随机场模型，包括：选取条件随机场模型的拓扑结构，选取条件随机场模型的特征函数；具体步骤如下：

2-1)建立条件随机场模型；在条件随机场模型中，将充电价格作显式随机变量，充电需求作为隐式随机变量；每个区域的每个时段分别对应一个充电价格和一个充电需求；将所有的显示随机变量构成图结构中的节点集合v，每一个显示随机变量都有一个对应的隐式随机变量，各随机变量之间的相关关系由连接两节点的边来表示；将各充电需求之间的连接的边的集合用边集e表示，e＝ek+et，边集e包括在空间上拓扑连接的边集ek和在时间上拓扑连接的边集et，其中ek表示在同一时段内所有区域的充电需求的空间相关关系，et表示在同一个区域中的不同时段充电需求的相关关系；节点集和边集组成的图为g＝(v，e)；

条件随机场模型中的充电价格与充电需求之间的关系如下：

其中：

其中，是归一化的充电需求组成的向量；是归一化后的充电需求向量；是条件随机场模型的未知参数，it，jt分别是第i个区域的第t个时段对应的图中的节点和第j个区域的第t个时段对应的图中的节点，分别是第i区域的第t1，t2个时段对应的图中的节点；ωi，i∈v是自弹性的参数，用来量化第i个节点的充电需求di和其对应的充电价格ρi之间的相关关系，与之匹配的特征函数为ψi(di，ρi)；是空间弹性的参数，用来量化第t个时段第i个区域和第j个区域间的充电需求之间的相关关系，与之匹配的特征函数为是空间弹性的参数，用来量化第i个区域中t1，t2时段间的充电需求之间的相关关系，与之匹配的特征函数为χ为充电需求的离散取值集合；|v|是边集中元素的数量；d∈χ^|v|表示了在χ中选取|v|次元素来构成充电需求的向量d；z(ρ)为配分函数；

2-2)选取需要研究的空间上充电需求相关关系，方法如下：首先选取感兴趣的区域，然后将每个感兴趣区域及该区域的相邻区域连接起来，所有连接的边表示了充电需求转移的路径，组成边集ek；

2-3)选取需要研究的时段上充电需求相关关系，方法如下：取每一个区域的各个时段，将该区域每一个时段的充电需求节点两两连接在一起，所有连接的边组成边集et；

2-4)选取条件随机场模型的三个特征函数和表达式分别如下：

ψi(di，ρi)＝diρi，i∈v

3)利用步骤1)中得到的训练集对步骤2)建立的条件随机场模型进行训练，得到训练完毕的条件随机场模型；具体步骤如下：

3-1)最大化似然函数；

求取未知参数ω，使得训练集出现的概率为最大；

ω的对数似然函数为：

lnl(d|ρ；ω)＝lnpω(d|ρ)

根据三个特征函数，该对数似然函数的梯度为：

其中e(·)为概率分布的期望；

3-2)采用带遗忘的随机梯度上升算法对条件随机场模型进行训练，得到训练完毕的条件随机场模型；具体步骤如下：

3-2-1)初始化参数ω⁰，设迭代次数n＝0，设定遗忘系数α，学习率γ，训练集的天数为n，对第i天的数据选择概率为

3-2-2)在训练集中利用每一天数据概率pi选取出第i天的充电需求和充电价格向量数据(di，ρi)；

3-2-3)计算第n次迭代的最大似然函数的梯度

3-2-4)更新参数ωⁿ⁺¹＝ωⁿ+γδωⁿ；

3-2-5)计算第i天数据的平均损失并判定：若该天的数据已经被选取次数为m次，则其中δ(i)表示选取到第i天数据时对应的迭代次数n的集合；

3-2-6)更改所有天数的数据被选取的概率：

3-2-7)对n进行判定：如果n达到最大迭代次数，则输出ωⁿ作为条件随机场模型的最优参数ω^*，条件随机场模型训练完毕，进入步骤4)；否则，令n＝n+1，然后重新返回步骤3-2-2)；

4)利用步骤3)训练完毕的条件随机场模型估计充电需求的时空价格弹性；具体步骤如下：

4-1)利用条件随机场中对有环图的环状信念传播算法，估计充电需求的概率分布；具体步骤如下：

4-1-1)初始化信息初始迭代次数n＝1，其中表示第n次迭代中，当节点j的充电需求从离散集合x中选取取值为dj时，从节点i传递到节点j的信息；

4-1-2)对所有的边(i，j)∈e和节点j的充电需求对应的所有离散取值dj∈x；计算节点i传递到节点j的信息其中n(i)表示与节点i相连接的节点集合，n(i)\{j}表示节点i相连接的节点且不包含节点j的集合，ωi，jψi，j(di，dj)表示充电需求之间的相关关系；

4-1-3)对同一节点j的不同信息进行归一化

4-1-4)判定：若达到收敛条件或者达到最大迭代次数，则转到4-1-5)运算；否则，令迭代次数n＝n+1，然后重新回到步骤4-1-2)；

4-1-5)根据收敛的信息计算信念，计算方法为：

4-1-6)对信念进行归一化为：

4-1-7)待求取的隐式随机变量的期望为：

4-2)在给定的充电价格处局部线性化得到充电需求的价格弹性；

第i个区域的t1时段充电价格对第j个区域t2时段充电需求的影响用价格弹性表示；以设定的长δρ在第i个区域t1时段给定的充电价格处，取其附近的两个充电价格并且保持其余的区域价格不变，由此得到包含所有区域所有时段的两个价格向量对两个价格向量分别使用步骤4-1)的环状信念传播算法，计算在两个充电价格向量下分别对应的第j个区域t2时段期望充电需求和得到充电需求的价格弹性表达式如下：

本发明的特点及有益效果：

1、本发明是一种数据驱动的充电价格弹性估计方法，利用了充电服务商在一段时间内的充电历史数据，得到的价格弹性结果会更加真实有效。

2、本发明重点体现了电动汽车充电需求在时间和空间上的转移，并用条件随机场模型同时建模了充电需求在时间和空间上的相关性。本发明还能因地制宜，通过调整拓扑图结构灵活调整需要考虑的充电需求相关关系，得到使用者需要的需求价格弹性。

3、本发明可以应用在电动汽车充电领域，根据本发明得到的充电需求的价格弹性结果，电网公司能够更有效掌握电动汽车用户对充电价格的响应，从而合理制定分时、分区域电价，引导充电负荷在不同时间不同地点的合理分布，从而在时间和空间上均衡电网容量利用率，减少电网容量的压力。

附图说明

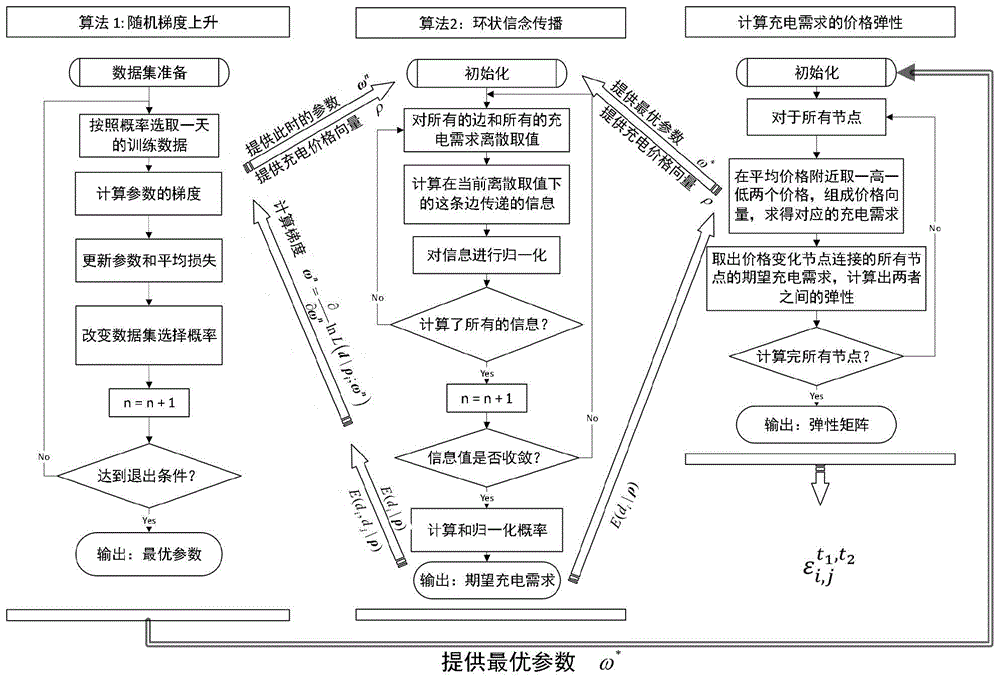
图1是本发明方法的整体流程图。

图2是本发明实施例中充电需求和充电价格在空间和时间上的拓扑图。

具体实施方式

本发明提出一种数据驱动的电动汽车充电需求的时空价格弹性估计方法，下面结合附图和具体实施例对本发明进一步详细说明如下。

本发明是在已知充电服务商历史充电记录的情况下，估算出电动汽车用户充电需求的时空价格弹性的方法。本发明适用于已经建成较多充电站的充电服务商，并且需要有一定的运营数据积累。

本发明提出一种数据驱动的电动汽车充电需求的时空价格弹性估计方法，该方法首先获取每个区域在研究时间内的充电历史数据，对历史数据进行归一化处理，得到各区域每日每时段归一化后的充电需求和充电价格并组成训练集；然后建立一个条件随机场模型，其中将充电价格作显式随机变量，充电需求作为隐式随机变量，确定条件随机场模型的拓扑结构及条件随机场模型的特征函数；利用训练集对条件随机场模型进行训练，得到训练完毕的条件随机场模型；利用训练完毕的条件随机场模型，计算任一区域任一时段充电价格对各区域任一时段充电需求的影响即得到时空价格弹性。

该方法整体流程如图1所示，包括以下步骤：

1)划分研究区域，获取每个区域在研究时间内的充电历史数据，对历史数据进行归一化处理，得到各区域每日每时段归一化后的充电需求和充电价格并组成训练集。

2)建立条件随机场模型，包括：选取条件随机场模型的拓扑结构，选取条件随机场模型的特征函数。

3)利用步骤1)中得到的训练集对步骤2)建立的条件随机场模型进行训练，得到训练完毕的条件随机场模型。

4)利用步骤3)训练完毕的条件随机场模型估计充电需求的时空价格弹性。

在上述方法中，所述步骤1)具体步骤如下：

1-1)将研究的地区(通常为城市)划分为若干块大小一样的区域，可以使用方格或者蜂巢状网络对该地区进行划分，通常可以划分为多个边长为3～5km的方形区域，记划分成的区域集合为该集合中共包含k个区域。

将一天的时间划分为t个时段，本实施例中按照类似于北京工商业电价的时段划分方式，将全天划分为三个时段，其中，峰时段：[10h，15h]∪[16h，17h]∪[18h，21h]、平时段：[7h，10h]∪[15h，16h]∪[17h，18h]∪[21h，23h]、谷时段：[23h，0h]∪[0h，7h]，记划分为的时段集合为其中，h代表峰时段，m代表平时段，l代表谷时段。

1-2)获取步骤1)划分的每一块区域中的所有充电站在研究时间(通常选取最近的一段时间)内(本实施例为最近的3个月)的充电记录，得到在研究时间内的每一个区域的每日平均充电量各区域充电站数量ni(个)。并且得到每一个区域在研究时间内选定时段范围内(通常为峰平谷三个时段)每日每时段总充电量研究时间内每日每时段加权度电充电价格研究时间内每时段日平均的加权度电充电价格/kwh)、研究时间内每时段日平均充电量其中下标表示第i个区域，上标表示第t个时段，τ表示第τ天。

1-3)对步骤1-2)获取的每一区域的和分别进行归一化，得到归一化后的各区域每日每时段总充电量(即归一化后的充电需求)和归一化的各区域加权度电充电价格(即归一化后的的充电价格)，归一化公式分别如下：

1-4)将归一化后的充电价格和充电需求组成训练集其中小括号代表一个区域在一个时段的充电需求和充电价格对，中括号表示第τ天中所有区域在所有时段的充电需求和充电价格对数据。

所述步骤2)具体步骤如下：

2-1)建立充电问题下的条件随机场模型。在条件随机场模型中，本发明将充电价格作显式随机变量，充电需求作为隐式随机变量。一个区域的一个时段对应着一个充电价格、一个充电需求。将所有的显示随机变量(即各区域在每个时段的充电需求)构成图结构中的节点集合v，每一个显示随机变量都有一个对应的隐式随机变量(充电价格)，各随机变量之间的相关关系由连接两节点的边来表示，包括：充电价格和对应的充电需求相关关系、充电需求之间的相关关系；将各充电需求之间的连接的边集合用边集e表示，再将边集e进一步拆分为e＝ek+et，包括了在空间上拓扑连接的边集ek和在时间上拓扑连接的边集et，其中ek表示在同一时段内所有区域的充电需求的空间相关关系，在本实施例中有三个时段，也即是ek由在三个时段上的三层相同的空间拓扑构成；et表示了在同一个区域中的不同时段充电需求的相关关系，在本实施例中有k个区域，也即是et由k个相同的时间拓扑构成。节点集和边集组成的图为g＝(v，e)，本实施如图2所示。条件随机场模型可以在已知充电价格后推断出充电需求。

条件随机场模型中的充电价格与充电需求之间的关系如下：

其中：

其中，是归一化的充电需求组成的向量，在本实施例中是归一化后的充电需求向量，在本实例中为了简化书写，下文用替代表示归一化后的价格和需求。是条件随机场模型的未知参数，此处it，jt分别指的是第i个区域的第t个时段对应的图中的节点和第j个区域的第t个时段对应的图中的节点，指的是第i区域的第t1，t2个时段对应的图中的节点。ωi，i∈v是自弹性的参数，用来量化第i个节点的充电需求di和其对应的充电价格ρi之间的相关关系(注意此处di的i指的是拓扑图中的第i个节点，而中的i指的是第i个区域)，与之匹配的特征函数为ψi(di，ρi)；是空间弹性的参数，用来量化第t个时段第i个区域和第j个区域间的充电需求之间的相关关系，与之匹配的特征函数为是空间弹性的参数，用来量化第i个区域中t1，t2时段间的充电需求之间的相关关系，与之匹配的特征函数为在本实施例中，χ为充电需求的离散取值集合。|v|是边集中元素的数量。所以d∈χ^|v|表示了在χ中选取|v|次元素来构成充电需求的向量d。配分函数z(ρ)是用来归一化概率的。和三个特征函数用来描述充电价格和充电需求的相关关系，空间上的充电需求的相关关系，时间上充电需求的相关关系。

2-2)选取需要研究的空间上充电需求相关关系。空间上的充电需求相关关系的建立：首先需要选取感兴趣的区域，通常为充电站数量较多，日平均充电量较大的区域(本实施例选取了10个区域)；然后将每个感兴趣区域及该区域的相邻区域连接起来，所有连接的边表示了充电需求转移的路径，组成边集ek；

2-3)选取需要研究的时段上充电需求相关关系。时间上的充电需求相关关系的建立：取每一个区域的各个时段，将该区域每一个时段的充电需求节点两两连接在一起，所有连接的边组成边集et。

本实施例组成最终的拓扑如图2所示。该拓扑按照时段分为峰平谷三层，其中白圈代表充电需求(隐式随机变量)，黑圈代表充电价格(显式随机变量)，连接线表示随机变量之间的相关关系。所以在图2中，既有充电价格与充电需求之间的相关关系，也有充电需求之间的相关关系。

2-4)选取条件随机场模型的三个特征函数和这三个特征函数分别描述了充电价格和充电需求的相关关系，充电需求的空间相关关系和充电需求的时间相关关系。可以选用为：

ψi(di，ρi)＝diρi，i∈v

所述步骤3)具体步骤如下：

3-1)最大化似然函数：求取未知参数ω，使得训练集出现的概率是最大的。

ω的对数似然函数为：

lnl(d|ρ；ω)＝lnpω(d|ρ)

根据三个特征函数，该对数似然函数的梯度为：

其中e(·)为概率分布的期望。

3-2)训练方法：采用带遗忘的随机梯度上升算法对条件随机场模型进行训练，得到训练完毕的条件随机场模型；其中，每一轮迭代中随机选取训练集中一天的充电价格和充电需求数据，用该天的数据进行一次梯度上升。异常数据的梯度绝对值都相对较大，在训练过程中利用梯度值逐步降低对异常数据的选取概率，算法内容如算法一所示：

在本实施例中，算法一中的参数设置如下：初始化参数用标准正态分布初始化，学习率为0.05，遗忘系数为5，训练天数为1000。

3-2-1)初始化参数ω⁰，设迭代次数n＝0，设定遗忘系数α，学习率γ，训练集的天数为n，对第i天的数据选择概率为

3-2-2)在训练集中利用每一天数据概率pi选取出第i天的充电需求和充电价格向量数据(di，ρi)。

3-2-3)计算出第n次迭代的最大似然函数的梯度在求充电需求期望时，需要用到步骤4-1-1)～4-1-7)的算法。

3-2-4)更新未知参数ωⁿ⁺¹＝ωⁿ+γδωⁿ；

3-2-5)计算第i天数据的平均损失并判定：若该天的数据已经被选取次数为m次，则其中δ(i)表示选取到第i天数据时对应的迭代次数n的集合。

3-2-6)更改所有天数的数据被选取的概率，以第i天为例：

3-2-7)对n进行判定：如果n达到最大迭代次数(本实施例中设置为5000次)，则输出当前的ωⁿ作为条件随机场模型的最优参数ω^*，条件随机场模型训练完毕，进入步骤4)；否则，令n＝n+1，然后重新返回步骤3-2-2)。

所述步骤4)具体步骤如下：

4-1)条件随机场中对有环图的环状信念传播算法：条件随机场模型的推断是在最优参数ω^*下，利用所有区域的充电价格d，推断出充电需求ρ的概率分布。如图2所示，最后选取的图通常是一个有环图。为了推断出充电需求的概率分布，其环状信念传播算法如下：

在本实施例中，算法2中的参数设置如下：初始化信息全为1，充电需求的离散集合为χ＝{-1，-0.5，0，0.5，1}，ε＝0.0001。为了书写方便，不再区分时间上的划分和空间上的划分，统一将充电需求之间的相关关系和写作ωi，jψi，j(di，dj)。

4-1-1)初始化信息初始迭代次数n＝1，其中表示第n次迭代中，当节点j的充电需求从离散集合χ中选取取值为dj时，从节点i传递到节点j的信息。

4-1-2)对所有的边(i，j)∈e和节点j的充电需求对应的所有离散取值dj∈x。计算节点i传递到节点j的信息其中n(i)表示与节点i相连接的节点集合，n(i)\{j}表示节点i相连接的节点且不包含节点j的集合。

4-1-3)对同一节点j的不同信息进行归一化

4-1-4)判定：若达到收敛条件或者达到最大迭代次数(本实施例中取值为100)，则跳转到4-1-5)运算；否则，令迭代次数n＝n+1，然后重新回到步骤4-1-2)；

4-1-5)根据收敛的信息计算信念，计算方法为：

4-1-6)对信念进行归一化为：

4-1-7)待求取的隐式随机变量的期望为：

4-2)在给定的充电价格处局部线性化得到充电需求的价格弹性：

第i个区域的t1时段充电价格对第j个区域t2时段充电需求的影响用价格弹性表示(i和j可以相同，t1，t2也可以相同)，以一个较小步长δρ(本实例给定为0.05元)，在第i个区域t1时段给定的充电价格(本实例给定为1元)处，取其附近的两个充电价格(本实例给定为1.05，0.95元)，并且保持其余的区域价格不变，由此得到包含所有区域所有时段的两个价格向量对两个价格向量分别使用4-1-1)-4-1-7)的环状信念传播算法，可以推断出在两个充电价格向量下对应的第j个区域t2时段期望充电需求由此可以得到充电需求的价格弹性，如下：

利用本发明求解出的价格弹性矩阵可以用于生成电网的最优运行策略和分时电价策略，相关的专利可参见cn202011014332.7和cn201910317334.4。

以上实例仅为用以说明本发明的技术方案而非对其限制，尽管参照上述实施例对本发明进行了详细的说明，所属领域的普通技术人员应当理解：依然可以对本发明的具体实施方式进行修改和等价替换，而未脱离本发明精神和范围的任何修改和等价替换，其均应涵盖在本发明的权利要求保护范围之中。