基于高斯过程回归的谐波源通用不确定性建模方法

1.本发明涉及一种基于高斯过程回归的谐波源通用不确定性建模方法。


背景技术：

2.近年来，电弧炉、电力机车等具有大容量、非线性、冲击性性质的负荷不断地大量接入电力系统，同时，电力电子技术在家用电器中的应用已十分普遍，这也使得居民负荷呈现出小容量、分散性的谐波源特性，使得中、低压配电网的谐波问题愈加严重，此外，谐波源的种类更加丰富多样，除了传统的电力机车、电弧炉等大容量非线性负荷，还有微网、分布式电源并网所需的换流器和采用电子电路的家用电器，而且电力电子电路拓扑和控制策略的多样性还会导致具体谐波特性的差异；其次，谐波产生的机理愈加复杂，谐波源的谐波发射特性不仅与自身的特点和工作状况有关，还会受到其他谐波源的影响，不仅如此，光伏、风电等分布式新能源受自然条件影响较大而具有间歇性，电动汽车充电桩的谐波特性与用户的使用习惯相关而存在时序上的规律性，即谐波源的谐波发射特性与电气量甚至非电气量均存在复杂的交互作用，这使得谐波源机理分析的难度日益增大
3.为了维持合格的电能质量，对谐波源进行建模以分析谐波产生的机理、谐波产生的影响、谐波源之间或谐波源与电网之间的交互影响是十分有必要的，是评估谐波危害和制定谐波抑制策略的前提，目前的谐波源模型可分为精确模型和通用模型：精确谐波源模型是通常用于深入研究某一类谐波源的谐波特性，因此其普适性不强，应用场景限制较大。因此频域角度分析谐波源外特性的通用模型是谐波源建模研究的重点。
4.目前的通用谐波源模型通常是将谐波源等效为基本电路元件的组合，利用其外端口电气量之间的关系是构建谐波源通用模型的最基本方法之一，如恒流源模型、诺顿等效模型等，但是谐波源种类繁多，谐波源的谐波发射特性与电气量甚至非电气量均存在复杂的交互作用，仅用电气量之间的关系来描述谐波源的谐波特性必然会产生偏差，而目前的通用模型均为精确值估计，难以充分反映未考虑到的物理因素对谐波源特性的不确定性影响，无法消除潜在的估计偏差。


技术实现要素：

5.本发明的目的在于提供一种基于高斯过程回归的谐波源通用不确定性建模方法，该方法所得到的估计结果是一个高斯分布，相比于精确值模型，可以从概率的意义上反映未考虑到的物理因素对谐波源特性的不确定性影响。同时，该建模方法具有精度高，参数求解方便等特点。此外，模型更新策略能够准确地跟踪谐波负荷的谐波特性变动，实现模型的在线更新，可以用于谐波应用于谐波负荷的异常行为和负荷变动监测等方面。
6.为实现上述目的，本发明的技术方案是：一种基于高斯过程回归的谐波源通用不确定性建模方法，基于谐波源外端口谐波电压和谐波电流之间的线性耦合关系，结合高斯过程回归实现谐波通用不确定性模型的建立。
7.在本发明一实施例中，一种基于高斯过程回归的谐波源通用不确定性建模方法实
现如下：
8.谐波监测数据采集；
9.用偏相关性进行谐波监测数据降维；
10.结合谐波机理，设置高斯过程回归的均值函数和协方差函数；
11.用极大似然法求解谐波通用不确定性模型参数，得到谐波源通用不确定性模型。
12.在本发明一实施例中，还包括对谐波通用不确定性模型的在线更新策略，在需要对谐波源进行实时监测分析的场景下，实现谐波通用不确定性模型的在线更新。
13.在本发明一实施例中，所述谐波监测数据采集，即采集谐波源外端口谐波电压和谐波电流；谐波源外特性可用谐波源外端口的各次谐波电流和谐波电压的线性关系近似表达，如下式表示：
[0014][0015]
式中，i
h
为第h次谐波电流；u
i
为第i次谐波电压；a
h,i
为第h次谐波电流和第i次谐波电压的耦合系数；b
h
为第h次谐波电流和基波电流i1的耦合系数；c
h
为常数，用来体现谐波源不受其他因素影响的固有谐波电流发射；可将式(1)写成矩阵形式，如下式所示：
[0016]
i
h
＝a
h
x+c
h
ꢀꢀꢀꢀꢀꢀ
(2)
[0017]
式中，a
h
＝[a
h,1
,a
h,2
,...,a
h,i
,b
h
]，为i+1维行向量；x＝[u1,u2,...,u
i
,i1]
t
，为i+1维列向量。
[0018]
在本发明一实施例中，所述用偏相关性进行谐波监测数据降维的实现方式如下：
[0019]
分别计算i
h
和变量u1,u2,...,u
i
,i1之间的偏相关系数记为r
m
(m＝1，2，
…
,i+1)；
[0020]
计算出偏相关性系数的均值
[0021]
挑选出偏相关系数r
m
大于均值r
av
所对应的变量，将这d个变量构成降维后的谐波通用不确定性模型参数x
d
＝[x1,x2,...,x
d
]，实现将谐波通用不确定性模型参数维度从m维降至d维。
[0022]
在本发明一实施例中，所述结合谐波机理，设置高斯过程回归的均值函数和协方差函数的实现方式如下：
[0023]
用偏相关性将谐波通用不确定性模型参数维度从m维降至d维后，对应的参数向量a
h
也降至d维，记为w
h
＝[z
h,1
,z
h,2
,...,z
h,d
]，因此式(2)可化为下式：
[0024]
i
h
＝w
h
x
d
+c
h
ꢀꢀꢀꢀꢀꢀꢀꢀ
(3)
[0025]
将式(3)作为高斯过程的均值函数；在选取协方差函数时，为能够充分反映不同变量对谐波特性的影响程度，应对每一个变量都赋予不同的参数，因此选取如下函数作为协方差函数：
[0026][0027]
式中x
im
为变量向量x
i
中的第m个变量，x
jm
为变量向量x
j
中的第m个变量；σ
f
为信号方差；σ
m
为方差尺度，体现了不同变量的影响能力。
[0028]
在本发明一实施例中，所述用极大似然法求解谐波通用不确定性模型参数，得到谐波源通用不确定性模型的实现方式如下：
[0029]
模型参数集合θ＝{σ
f
；σ
m
；w
h
；c
h
}即为待辨识的超参数，用极大似然法进行参数辨识；训练集样本条件概率的负对数似然函数为l(θ)＝
‑
logp(y|x,θ)，令其对超参数θ求偏导，然后用共轭梯度法对偏导数进行最小化以得到最优的超参数；负对数似然函数l(θ)以及关于超参数θ偏导数可由下式表示：
[0030][0031][0032]
其中α＝c
‑1y；
[0033]
辨识出模型的超参数θ＝{σ
f
；σ
m
；w
h
；c
h
}后，利用式(7)和(8)便可预测变量x
*
的预测结果y
*
的高斯分布均值和方差cov(y
*
)；
[0034][0035][0036]
在本发明一实施例中，所述谐波通用不确定性模型的在线更新策略实现方式如下：
[0037]
引入两个需要用到的指标：命中率和变异系数；命中率表示实际谐波电流值落在所选定置信区间的比例，反映预测结果的准确程度，设一次预测中n个预测结果中有m个点落在所选定置信区间中，则此次预测的命中率为：
[0038][0039]
变异系数则反映了预测结果的离散程度，如果某个预测结果变异系数大于15％，则认为数据的离散程度过大，预测的结果不正常，视为没有命中预测区间；变异系数的定义如下：
[0040][0041]
式中和d
n*
分别为第n次预测结果的均值和标准差；
[0042]
谐波通用不确定性模型的在线更新策略的具体步骤如下：
[0043]
1)用离线数据或历史数据构建好谐波源通用不确定性模型；
[0044]
2)设定监测尺度数据点数d和命中率阈值t；
[0045]
3)以d为滚动的分析窗口，将实时监测数据输入用离线数据或历史数据构建好的谐波源通用不确定性模型，对比分析实测谐波电流和模型预测出的谐波电流分布，计算命中率和变异系数；
[0046]
4)在数据长度为d的某一段时间内，如果命中率大于t，则不更新谐波源通用不确定性模型，进入下一个分析窗口；如果命中率小于阈值t，则认为此时负荷发生长时间异常运行或变动，则用储存的d个监测数据来更新谐波源通用不确定性模型；
[0047]
循环步骤3)
‑
4)。
[0048]
本发明还提供了一种计算机可读存储介质，其上存储有能够被处理器运行的计算
机程序指令，当处理器运行该计算机程序指令时，能够实现如上述所述的方法步骤。
[0049]
相较于现有技术，本发明具有以下有益效果：本发明一种基于高斯过程回归的谐波源通用不确定性建模方法，所得到的估计结果是一个高斯分布，相比于精确值模型，可以从概率的意义上反映未考虑到的物理因素对谐波源特性的不确定性影响。同时，该建模方法具有精度高，参数求解方便等特点。此外，模型更新策略能够准确地跟踪谐波负荷的谐波特性变动，实现模型的在线更新，可以用于谐波应用于谐波负荷的异常行为和负荷变动监测等方面。
附图说明
[0050]
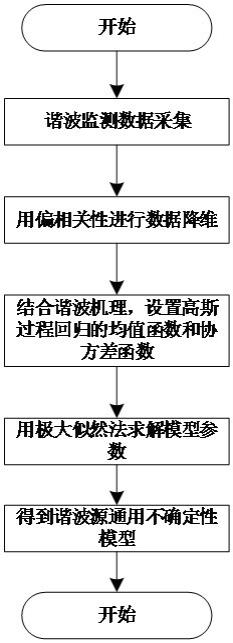
图1为本发明基于高斯过程回归的谐波源通用不确定性模型建模流程。
[0051]
图2为本发明模型在线更新策略流程图。
具体实施方式
[0052]
下面结合附图，对本发明的技术方案进行具体说明。
[0053]
应该指出，以下详细说明都是示例性的，旨在对本申请提供进一步的说明。除非另有指明，本文使用的所有技术和科学术语具有与本申请所属技术领域的普通技术人员通常理解的相同含义。
[0054]
需要注意的是，这里所使用的术语仅是为了描述具体实施方式，而非意图限制根据本申请的示例性实施方式。如在这里所使用的，除非上下文另外明确指出，否则单数形式也意图包括复数形式，此外，还应当理解的是，当在本说明书中使用术语“包含”和/或“包括”时，其指明存在特征、步骤、操作、器件、组件和/或它们的组合。
[0055]
本发明一种基于高斯过程回归的谐波源通用不确定性建模方法，基于谐波源外端口谐波电压和谐波电流之间的线性耦合关系，结合高斯过程回归实现谐波通用不确定性模型的建立。还包括对谐波通用不确定性模型的在线更新策略，在需要对谐波源进行实时监测分析的场景下，实现谐波通用不确定性模型的在线更新。
[0056]
以下为本发明实施例具体实现过程。
[0057]
如图1所示，本发明一种基于高斯过程回归的谐波源通用不确定性建模方法，包括：
[0058]
(1)基于谐波源外端口谐波电压和谐波电流之间的线性耦合关系，结合高斯过程回归提出了一种谐波通用不确定性建模方法。
[0059]
(2)基于上述的建模方法，提出了一种模型在线更新策略，可以在需要对谐波源进行实时监测分析的场景下，实现模型的在线更新，而且可以应用于谐波负荷的异常行为和负荷变动监测等方面。
[0060]
1、高斯过程回归
[0061]
高斯过程是一种统计学习方法，也是一种基于贝叶斯框架的监督式学习的机器学习方法，其定义的表述为：高斯过程是一个随机变量的集合，其任意有限的随机变量都符合高斯分布。
[0062]
一个高斯过程的性质可以用它的均值函数m(x)和协方差函数k(x,x')确定，写作：
[0063]
f～gp(m(x),k(x,x'))
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(1)
[0064]
式中x,x'∈r
n
为随机变量，均值函数和协方差函数由下式定义：
[0065][0066]
均值函数m(x)表示在没有任何观测值时对函数值的期望，为了方便说明，这里将m(x)设为0。协方差函数k(x,x')用于衡量输入样本之间的相似程度，输入样本相似程度越大，越可能获得相近的输出值，其值和协方差函数的选取有关，协方差函数是一个满足mercer条件的对称函数，常用的有平方指数协方差函数、matern协方差函数等，应根据所要解决的问题选择合适的协方差函数。对于回归问题，考虑如下模型：
[0067]
y＝f(x)+ε
ꢀꢀꢀꢀꢀꢀ
(3)
[0068]
式中x为n维随机向量；f为函数值；y为受到噪声污染的观测值；ε为独立高斯白噪声，假设则观测值y的先验分布为：
[0069][0070]
观测值y和预测值y
*
的联合先验分布为：
[0071][0072]
式中k(x,x)为n
×
n阶对称正定的协方差矩阵；矩阵元素k
ij
＝k(x
i
,x
j
)是用于度量x
i
和x
j
相似程度的协方差函数；k(x
*
,x)＝k(x,x
*
)
t
为用于预测y
*
的变量x
*
与训练集的输入x之间的n
×
1阶协方差矩阵；k(x
*
,x
*
)为x
*
自身的协方差；i
n
为n维单位矩阵。
[0073]
由此可以计算出预测值y
*
的后验分布为：
[0074][0075]
其中
[0076][0077][0078]
式中和cov(y
*
)即为变量x
*
对于预测结果y
*
的高斯分布的均值和方差。
[0079]
2、基于高斯过程回归的谐波源通用不确定性模型
[0080]
2.1、均值函数和协方差函数的选取
[0081]
谐波源外特性可用谐波源端口的各次谐波电流和谐波电压的线性关系近似表达，如下式表示：
[0082][0083]
式中，i
h
为第h次谐波电流；u
i
为第i次谐波电压；a
h,i
为第h次谐波电流和第i次谐波电压的耦合系数；b
h
为h次谐波电流和基波电流的耦合系数；c
h
为常数，用来体现谐波源不受其他因素影响的固有谐波电流发射。可以将式(9)写成矩阵形式，如下式所示：
[0084]
i
h
＝a
h
x+c
h
ꢀꢀꢀꢀꢀꢀꢀ
(10)
[0085]
式中，a
h
＝[a
h,1
,a
h,2
,...,a
h,i
,b
h
]，为i+1维行向量；x＝[u1,u2,...,u
i
,i1]
t
，为i+1维列向量。
[0086]
为了减少所需辨识的模型参数以简化模型结构，可以采用偏相关性分析来对变量
进行筛选，达到对模型参数x进行降维的目的，具体步骤如下：
[0087]
(1)分别计算i
h
和变量u1,u2,...,u
i
,i1之间的偏相关系数记为r
m
(m＝1，2，
…
,i+1)；
[0088]
(2)计算出偏相关性系数的均值
[0089]
(3)挑选出偏相关系数r
m
大于均值r
av
所对应的变量，将这d个变量构成降维后的模型参数x
d
＝[x1,x2,...,x
d
]，实现将模型参数维度从m维降至d维。
[0090]
(4)对应的参数向量a
h
也降至d维，记为w
h
＝[z
h,1
,z
h,2
,...,z
h,d
]，式(10)可化为下式：
[0091]
i
h
＝w
h
x
d
+c
h
ꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(11)
[0092]
将式(11)作为高斯过程的均值函数。在选取协方差函数时，为了能够充分反映不同变量对谐波特性的影响程度，应对每一个变量都赋予不同的参数，因此选取如下函数作为协方差函数：
[0093][0094]
式中x
im
为变量向量x
i
中的第m个变量，x
jm
同理；σ
f
为信号方差；σ
m
方差尺度，体现了不同变量的影响能力。
[0095]
2.2、模型参数的求解
[0096]
模型参数集合θ＝{σ
f
；σ
m
；w
h
；c
h
}即为待辨识的超参数，用极大似然法进行参数辨识。训练集样本条件概率的负对数似然函数为l(θ)＝
‑
logp(y|x,θ)，令其对超参数θ求偏导，然后用共轭梯度法对偏导数进行最小化以得到最优的超参数。负对数似然函数l(θ)以及关于超参数θ偏导数可由下式表示：
[0097][0098][0099]
其中α＝c
‑1y。
[0100]
2.3、模型的结果预测
[0101]
辨识出模型的超参数θ＝{σ
f
；σ
m
；w
h
；c
h
}后，利用式(7)和(8)便可以预测变量x
*
的预测结果y
*
的高斯分布的均值和方差cov(y
*
)。假设实际的谐波电流值集合为y＝{y1,y2,...,y
n
}，模型估计结果的均值集合为方差集合为s
*
＝{s
1*
,s
2*
,...,s
n*
}，则亦可得到标准差集合为d
*
＝{d
1*
,d
2*
,...,d
n*
}。则可以根据不同的置信程度需求决定置信区间的大小，用置信区间来描述预测结果的分布情况，本文以99.7％置信区间为例，即实际谐波电流值有99.7％的概率落在这个区间内。95.45％置信区间和68.27％置信区间同理。该模型预测的结果谐波电流值的分布，从概率的角度反映了可能存在的估计偏差和谐波源的不确定行为，以便在定制谐波预防、治理策略时，能根据系统保守度、冗余度的要求更加灵活地制定方案。
[0102]
3、模型在线更新策略
[0103]
理论上，在确保本文所提方法准确性的情况下，实测谐波电流值应当均落在模型预测的置信区间内，若出现大量的实测值偏离预测的置信区间，则说明谐波源的谐波特性发生改变或多谐波源复杂网络中的负荷发生异动等情况，所构建好的模型已经不能很好地描述变化后谐波特性。基于上述分析，在需要对谐波源进行实时监测分析的场景下，提出了一种模型在线更新策略。
[0104]
在详细说明更新策略之前，引入两个需要用到的指标:命中率和变异系数。命中率表示实际谐波电流值落在所选定置信区间(如99.7％置信区间)的比例，反映了预测结果的准确程度，设一次预测中n个预测结果中有m个点落在99.7％置信区间中，则此次预测的命中率为：
[0105][0106]
变异系数则反映了预测结果的离散程度，如果某个预测结果变异系数大于15％，则认为数据的离散程度过大，预测的结果不正常，视为没有命中预测区间。变异系数的定义如下：
[0107][0108]
如图2所示，模型的在线更新策略如下：
[0109]
(1)用离线数据或历史数据用上述方法构建好谐波源通用不确定性模型；
[0110]
(2)设定监测尺度数据点数d和命中率阈值t；
[0111]
(3)以d为滚动的分析窗口，将实时监测数据输入用离线数据或历史数据构建好的谐波源模型，对比分析实测谐波电流和模型预测出的谐波电流分布，计算命中率和变异系数；
[0112]
(4)在数据长度为d的某一段时间内，如果命中率大于阈值t，则不更新模型，进入下一个分析窗口；如果命中率指标小于阈值t，则认为此时负荷发生长时间异常运行或变动，则用储存的d个监测数据来更新模型；
[0113]
(5)循环步骤(3)
‑
(4)。
[0114]
本领域内的技术人员应明白，本申请的实施例可提供为方法、系统、或计算机程序产品。因此，本申请可采用完全硬件实施例、完全软件实施例、或结合软件和硬件方面的实施例的形式。而且，本申请可采用在一个或多个其中包含有计算机可用程序代码的计算机可用存储介质(包括但不限于磁盘存储器、cd
‑
rom、光学存储器等)上实施的计算机程序产品的形式。
[0115]
本申请是参照根据本申请实施例的方法、设备(系统)、和计算机程序产品的流程图和/或方框图来描述的。应理解可由计算机程序指令实现流程图和/或方框图中的每一流程和/或方框、以及流程图和/或方框图中的流程和/或方框的结合。可提供这些计算机程序指令到通用计算机、专用计算机、嵌入式处理机或其他可编程数据处理设备的处理器以产生一个机器，使得通过计算机或其他可编程数据处理设备的处理器执行的指令产生用于实现在流程图一个流程或多个流程和/或方框图一个方框或多个方框中指定的功能的装置。
[0116]
这些计算机程序指令也可存储在能引导计算机或其他可编程数据处理设备以特
定方式工作的计算机可读存储器中，使得存储在该计算机可读存储器中的指令产生包括指令装置的制造品，该指令装置实现在流程图一个流程或多个流程和/或方框图一个方框或多个方框中指定的功能。
[0117]
这些计算机程序指令也可装载到计算机或其他可编程数据处理设备上，使得在计算机或其他可编程设备上执行一系列操作步骤以产生计算机实现的处理，从而在计算机或其他可编程设备上执行的指令提供用于实现在流程图一个流程或多个流程和/或方框图一个方框或多个方框中指定的功能的步骤。
[0118]
以上所述，仅是本发明的较佳实施例而已，并非是对本发明作其它形式的限制，任何熟悉本专业的技术人员可能利用上述揭示的技术内容加以变更或改型为等同变化的等效实施例。但是凡是未脱离本发明技术方案内容,依据本发明的技术实质对以上实施例所作的任何简单修改、等同变化与改型，仍属于本发明技术方案的保护范围。