一种基于ORC采样和QGPCE变换的弥散张量图像鲁棒零水印方法

一种基于orc采样和qgpce变换的弥散张量图像鲁棒零水印方法
技术领域
1.本发明涉及医学图像安全的技术领域，尤其涉及一种基于orc采样和qgpce变换的弥散张量图像鲁棒零水印方法。


背景技术：

2.弥散张量成像(diffusion tensor imaging，dti)是一种新型的磁共振成像技术，被广泛应用于大脑白质纤维建模、活体心脏心肌纤维建模和中枢神经系统等疾病的辅助诊断，随着远程医疗诊断技术的普及，使得越来越多的dti数据应用于医学诊断和科学研究，而未被保护的dti图像在网络中传输和使用，极易遭受非法拷贝和篡改等攻击，因而对病人隐私和临床诊断造成严重损害；同时dti图像是一个nd(n＝4,5)的体数据结构，其中每个体素是一个二阶三维张量，一般针对二维或者三维医学图像的版权保护算法，很难直接应用于dti图像，通过查阅大量文献发现针对dti图像的版权保护研究几乎无人涉及，为防止未授权的dti图像被非法拷贝或篡改，对dti图像进行版权保护和完整性严重具有重要的意义和价值。
3.近年来，人们提出一些解决图像安全问题的技术，包括图像加密技术和数字水印技术，其中，数字水印技术主要用于实现数字图像的版权保护，它将特征或数字信息嵌入到图像中，确保经过数据处理后，数字水印可以完整地从图像中提取出来，从而达到版权保护和完整性验证等目的。
4.但是，嵌入的水印信息会破坏医学图像的完整性，而医学图像中含有的重要的病理诊断信息，有可能会因为水印的加入而产生变化，进而影响医生对于病人病情的正确判断，由于医学图像对完整性和安全性较高，因此针对医学图像的水印研究主要集中于可逆水印和零水印；近年来，零水印的研究取得了很大的进展，但是目前的零水印方案主要是针对于二维图像进行版权保护，因此如何实现dti图像的版权保护至关重要。


技术实现要素：

5.本部分的目的在于概述本发明的实施例的一些方面以及简要介绍一些较佳实施例。在本部分以及本申请的说明书摘要和发明名称中可能会做些简化或省略以避免使本部分、说明书摘要和发明名称的目的模糊，而这种简化或省略不能用于限制本发明的范围。
6.鉴于上述现有存在的问题，提出了本发明。
7.因此，本发明提供了一种基于orc采样和qgpce变换的弥散张量图像鲁棒零水印方法，能够解决高维医学图像版权存在安全隐患风险的问题。
8.为解决上述技术问题，本发明提供如下技术方案：包括，根据dti图像数据构建空间张量描述场；利用光线投射采样策略对所述dti图像进行正交投射采样，获得基于冠状面、矢状面和横切面的三张正交特征投射图像；将所述三张正交特征投射图像作为四元数的三个虚部，计算其qgpce变换系数以构建特征图像；对混沌置乱的所述特征图像和水印图
像进行异或操作获得零水印图像。
9.作为本发明所述的基于orc采样和qgpce变换的弥散张量图像鲁棒零水印方法的一种优选方案，其中：构建所述空间张量描述场包括，
10.t＝{d
′
xyz
|x∈[1,n
x
],y∈[1,n
y
],z∈[1,n
z
]}
[0011]
其中，将所述dti图像f
d
中的每一个弥散张量体素d进行张量分解为d
′
，得到dti图像特征值和特征向量形式t，d
′
xyz
是其中一个弥散张量体素d
xyz
的特征值和特征向量形式，(x,y,z)表示了弥散张量体素d在f
d
空间下的局部空间坐标，(n
x
,n
y
,n
z
)表示dti图像的三维空间最大尺寸。
[0012]
作为本发明所述的基于orc采样和qgpce变换的弥散张量图像鲁棒零水印方法的一种优选方案，其中：所述光线投射采样策略包括，将所述dti图像表示的生理解剖结构特征进行降维表示；采样解剖结构方向与投射光线方向相一致的弥散张量体素；将采样值在二维图像空间进行合成，获得二维投射采样特征图；
[0013][0014]
其中，r为给定光线矩阵，r
1 r
2 r3分别表示垂直于冠状面，矢状面和横切面三个方向的正交光线，根据光线矩阵r对dti图像同时进行冠状面、矢状面和横切面的采样。
[0015]
作为本发明所述的基于orc采样和qgpce变换的弥散张量图像鲁棒零水印方法的一种优选方案，其中：还包括，计算弥散张量体素d
′
xyz
的长轴方向e1与光线r
i
(i＝1,2,3)之间的空间锐角夹角值θ
re
(θ
re
∈[0,90])；当a越趋近于1时，则所述弥散张量体素d
′
xyz
的长轴方向e1与光线r
i
(i＝1,2,3)的方向具有越高的一致性，如下，
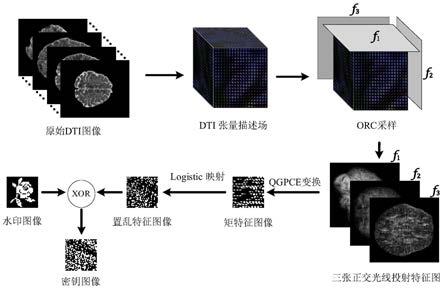
[0016][0017]
其中，令为弥散张量体素d
′
xyz
在光线r
i
投射过程中的采样值，p为给定阈值，λ3表示该d
′
的短轴的长度，s
′
表示沿光线r
i
方向，d
′
xyz
的下一个相邻的弥散张量体素的光线投射采样值，即当r
i
＝r1＝[1 0 0]
t
时，
[0018][0019]
a∈[0，1]，p∈(0，1)，i∈{1，2，3}。
[0020]
作为本发明所述的基于orc采样和qgpce变换的弥散张量图像鲁棒零水印方法的一种优选方案，其中：还包括，根据给定的光线矩阵r和dti图像的张量描述场t，利用采样方程计算张量描述场t的每一个d
′
xyz
，获得大小为(n
x
，n
y
，n
z
，i)的采样矩阵m，定义如下，
[0021][0022]
所述采样方程，如下，
[0023][0024]
其中，f1(y，z)是在垂直于冠状面的x轴方向合成的冠状面投影特征图，通过沿着r1方向，将采样矩阵m中的每一个采样值在二维图像空间f1(y，z)里进行累加合成，f2(x，z)和f3(x，y)分别为在垂直于矢状面的y轴方向和垂直于横切面的z轴方向合成的矢状面和横切面的投影特征图。
[0025]
作为本发明所述的基于orc采样和qgpce变换的弥散张量图像鲁棒零水印方法的一种优选方案，其中：所述极复指数变换包括，定义灰度图像f
g
(r，θ)的阶数为n(n＝0，1，...，∞)，则得到迭代次数为m(|m|＝0，1，...，∞)，参数为s的泛型极复指数(gpce)变换系数，如下，
[0026][0027]
其中，r
ns
(r)为径向基函数，*表示复数共轭，为虚数单位。
[0028]
作为本发明所述的基于orc采样和qgpce变换的弥散张量图像鲁棒零水印方法的一种优选方案，其中：还包括，根据四元数理论，将三幅大小相同特征图像视为一个纯四元数阵列的三个虚部，则利用纯四元数阵列的形式表示三张采样特征图，如下，
[0029]
f(r，θ)＝f1(r，θ)i+f2(r，θ)j+f3(r，θ)k
[0030]
其中，f1、f2和f3表示在极坐标下三幅光线投射采样特征图像，通过f(r，θ)可以把三张特征图像视为一个整体来描述；
[0031][0032][0033][0034][0035][0036]
其中，re(g)表示复数的实部，im(g)表示复数的虚部，g
nms
(f1)、g
nms
(f2)和g
nms
(f3)分别为三张投射特征图的泛型极复指数(gpce)变换系数/矩，为qgpce变换系数。
[0037]
作为本发明所述的基于orc采样和qgpce变换的弥散张量图像鲁棒零水印方法的一种优选方案，其中：包括，计算获得宿主dti图像f
d
的三张正交光线投射特征图f1，f2，f3；利用所述f1，f2，f3获得qgpce变换系数q，定义为三张投射特征图的正交矩，其矩容量为l＝
(2n+1)(2m+1)；将伪随机序列作为密钥k1，根据给定的二值水印图像w＝{f
w
(i，j)|i∈[1，n
h
]，j∈[1，n
w
]∩n
h
×
n
w
≤l}，从q中选择n
h
×
n
w
个矩作为矩向量v
m
＝{v
i
|i∈[1，n
h
×
n
w
]}；
[0038]
根据矩向量v
m
计算幅值获得幅向量a
m
＝{a
i
|i∈[1，n
h
×
n
w
]}，将a
m
构造为二维矩矩阵，h＝{f
h
(i，j)|i∈[1，n
h
]，j∈[1，n
w
]}作为二维矩特征图像；对矩特征图像h使用logistic映射进行加密，如下，
[0039]
x
i+1
＝λx
i
(1
‑
x
i
)，i＝0，1，2，...
[0040]
其中，x
i
∈[0，1]，λ∈[0，4]为控制参数，令λ＝4，保证混沌系统在[0，1]之间的均匀映射，给定初始值x0作为密钥k2生成长度为n
h
×
n
w
的混沌序列l，再将其进行二值化获得二值混沌序列l
b
，t为给定阈值，令t＝0.5，如下，
[0041][0042]
利用异或操作，将l
b
对h
b
进行加密，获得加密矩特征图像h
l
，如下，
[0043][0044]
对混沌序列h
l
和二值水印图像w进行异或操作获得密钥图像k＝{f
k
(i，j)|i∈[1，n
h
]，j∈[1，n
w
]}，如下，
[0045][0046]
其中，表示异或操作，将(w，k1，k2，k)作为原始图像的验证密钥存储在第三方版权中心。
[0047]
作为本发明所述的基于orc采样和qgpce变换的弥散张量图像鲁棒零水印方法的一种优选方案，其中：还包括，计算提取待验证dti图像f
′
d
的三张正交光线投射特征图f
′1，f
′2，f
′3；利用f
′1，f
′2，f
′3获得qgpce变换系数q
′
；基于从版权方获取的密钥k1，从q
′
中选择n
h
×
n
w
个矩作为矩向量v
′
m
＝{v
′
i
|i∈[1，n
h
×
n
w
]}；根据矩向量v
′
m
计算幅值获得幅向量a
′
m
＝{a
′
i
|i∈[1，n
h
×
n
w
]}，将a
′
m
构造为二维矩矩阵，h
′
＝{h
′
i
(i，j)|i∈[1，n
h
]，j∈[1，n
w
]}作为二维矩特征图像；对矩特征图像h
′
进行logistic映射加密，使用从版权方获取的密钥k2作为初始值x0生成长度为2n
w
的混沌序列l
′
；将其进行二值化获得二值混沌序列l
′
b
，利用异或操作用l
′
b
对h
′
进行加密，获得加密矩特征图像h
′
l
；对混沌序列h
′
l
和从版权方获取的密钥图像k进行异或操作获得水印图像w
′
＝{f
′
w
(i，j)|i∈[1，n
h
]，j∈[1，n
w
]}，通过评价w
′
完成版权验证。
[0048]
本发明的有益效果：本发明针对dti图像数据进行版权保护，提高了水印算法的效率，节省了水印存储空间，该算法能够有效抵抗常见的图像处理攻击和几何攻击，能够很好的应用于dtind(n＝4，5)高维医学图像的版权保护，非常适用于dti图像数据的版权保护。
附图说明
[0049]
为了更清楚地说明本发明实施例的技术方案，下面将对实施例描述中所需要使用的附图作简单地介绍，显而易见地，下面描述中的附图仅仅是本发明的一些实施例，对于本领域普通技术人员来讲，在不付出创造性劳动性的前提下，还可以根据这些附图获得其它的附图。其中：
[0050]
图1为本发明一个实施例所述的基于orc采样和qgpce变换的弥散张量图像鲁棒零
水印方法的流程示意图；
[0051]
图2为本发明一个实施例所述的基于orc采样和qgpce变换的弥散张量图像鲁棒零水印方法的dti张量描述场t的三维欧几里得空间示意图；
[0052]
图3为本发明一个实施例所述的基于orc采样和qgpce变换的弥散张量图像鲁棒零水印方法的光线r的光线采样示意图；
[0053]
图4为本发明一个实施例所述的基于orc采样和qgpce变换的弥散张量图像鲁棒零水印方法的高斯噪声和椒盐噪声对比示意图；
[0054]
图5为本发明一个实施例所述的基于orc采样和qgpce变换的弥散张量图像鲁棒零水印方法的压缩攻击示意图；
[0055]
图6为本发明一个实施例所述的基于orc采样和qgpce变换的弥散张量图像鲁棒零水印方法的中值滤波和高斯低通滤波示意图；
[0056]
图7为本发明一个实施例所述的基于orc采样和qgpce变换的弥散张量图像鲁棒零水印方法的单轴旋转示意图；
[0057]
图8为本发明一个实施例所述的基于orc采样和qgpce变换的弥散张量图像鲁棒零水印方法的缩放攻击示意图；
[0058]
图9为本发明一个实施例所述的基于orc采样和qgpce变换的弥散张量图像鲁棒零水印方法的左上角裁剪示意图。
具体实施方式
[0059]
为使本发明的上述目的、特征和优点能够更加明显易懂，下面结合说明书附图对本发明的具体实施方式做详细的说明，显然所描述的实施例是本发明的一部分实施例，而不是全部实施例。基于本发明中的实施例，本领域普通人员在没有做出创造性劳动前提下所获得的所有其他实施例，都应当属于本发明的保护的范围。
[0060]
在下面的描述中阐述了很多具体细节以便于充分理解本发明，但是本发明还可以采用其他不同于在此描述的其它方式来实施，本领域技术人员可以在不违背本发明内涵的情况下做类似推广，因此本发明不受下面公开的具体实施例的限制。
[0061]
其次，此处所称的“一个实施例”或“实施例”是指可包含于本发明至少一个实现方式中的特定特征、结构或特性。在本说明书中不同地方出现的“在一个实施例中”并非均指同一个实施例，也不是单独的或选择性的与其他实施例互相排斥的实施例。
[0062]
本发明结合示意图进行详细描述，在详述本发明实施例时，为便于说明，表示器件结构的剖面图会不依一般比例作局部放大，而且所述示意图只是示例，其在此不应限制本发明保护的范围。此外，在实际制作中应包含长度、宽度及深度的三维空间尺寸。
[0063]
同时在本发明的描述中，需要说明的是，术语中的“上、下、内和外”等指示的方位或位置关系为基于附图所示的方位或位置关系，仅是为了便于描述本发明和简化描述，而不是指示或暗示所指的装置或元件必须具有特定的方位、以特定的方位构造和操作，因此不能理解为对本发明的限制。此外，术语“第一、第二或第三”仅用于描述目的，而不能理解为指示或暗示相对重要性。
[0064]
本发明中除非另有明确的规定和限定，术语“安装、相连、连接”应做广义理解，例如：可以是固定连接、可拆卸连接或一体式连接；同样可以是机械连接、电连接或直接连接，
也可以通过中间媒介间接相连，也可以是两个元件内部的连通。对于本领域的普通技术人员而言，可以具体情况理解上述术语在本发明中的具体含义。
[0065]
实施例1
[0066]
参照图1，为本发明的第一个实施例，提供了一种基于orc(orthogonal ray casting，正交光线投射)采样和qgpce(generic extremely complex index，泛型极复指数)变换的弥散张量图像鲁棒零水印方法，包括：
[0067]
s1：根据dti图像数据构建空间张量描述场。参照图2，其中需要说明的是，构建空间张量描述场包括：
[0068]
t＝{d
′
xyz
|x∈[1，n
x
]，y∈[1，n
y
]，z∈[1，n
z
]}
[0069]
其中，将dti图像f
d
中的每一个弥散张量体素d进行张量分解为d
′
，得到dti图像特征值和特征向量形式t，d
′
xyz
是一个弥散张量体素d
xyz
的特征值和特征向量形式，(x，y，z)表示了弥散张量体素d在f
d
空间下的局部空间坐标，(n
x
，n
y
，n
z
)表示dti图像的三维空间最大尺寸。
[0070]
s2：利用光线投射采样策略对dti图像进行正交投射采样，获得基于冠状面、矢状面和横切面的三张正交特征投射图像。参照图3，本步骤需要说明的是，光线投射采样策略包括：
[0071]
将dti图像表示的生理解剖结构特征进行降维表示；
[0072]
采样解剖结构方向与投射光线方向相一致的弥散张量体素；
[0073]
将采样值在二维图像空间进行合成，获得二维投射采样特征图；
[0074][0075]
其中，r为给定光线矩阵，r
1 r
2 r3分别表示垂直于冠状面，矢状面和横切面三个方向的正交光线，根据光线矩阵r对dti图像同时进行冠状面、矢状面和横切面的采样；
[0076]
计算弥散张量体素d
′
xyz
的长轴方向e1与光线r
i
(i＝1，2，3)之间的空间锐角夹角值θ
re
(θ
re
∈[0，90])；
[0077]
当a越趋近于1时，则弥散张量体素d
′
xyz
的长轴方向e1与光线r
i
(i＝1，2，3)的方向具有越高的一致性，如下，
[0078][0079]
其中，令为弥散张量体素d
′
xyz
在光线r
i
投射过程中的采样值，p为给定阈值，λ3表示该d
′
的短轴的长度，s
′
表示沿光线r
i
方向，d
′
xyz
的下一个相邻的弥散张量体素的光线投射采样值，即当r
i
＝r1＝[1 0 0]
t
时，
[0080][0081]
a∈[0，1]，p∈(0，1)，i∈{1，2，3}
[0082]
根据给定的光线矩阵r和dti图像的张量描述场t，利用采样方程计算张量描述场t的每一个d
′
xyz
，获得大小为(n
x
，n
y
，n
z
，i)的采样矩阵m，定义如下，
[0083][0084]
采样方程，如下，
[0085][0086]
其中，f1(y，z)是在垂直于冠状面的x轴方向合成的冠状面投影特征图，通过沿着r1方向，将采样矩阵m中的每一个采样值在二维图像空间f1(y，z)里进行累加合成，f2(x，z)和f3(x，y)分别为在垂直于矢状面的y轴方向和垂直于横切面的z轴方向合成的矢状面和横切面的投影特征图。
[0087]
s3：将三张正交特征投射图像作为四元数的三个虚部，计算其qgpce变换系数以构建特征图像。其中还需要说明的是，极复指数变换包括：
[0088]
定义灰度图像f
g
(r，θ)的阶数为n(n＝0，1，...，∞)，则得到迭代次数为m(|m|＝0，1，...，∞)，参数为s的泛型极复指数(gpce)变换系数，如下，
[0089][0090]
其中，r
ns
(r)为径向基函数，*表示复数共轭，为虚数单位；
[0091]
根据四元数理论，将三幅大小相同特征图像视为一个纯四元数阵列的三个虚部，则利用纯四元数阵列的形式表示三张采样特征图，如下，
[0092]
f(r，θ)＝f1(r，θ)i+f2(r，θ)j+f3(r，θ)k
[0093]
其中，f1、f2和f3表示在极坐标下三幅光线投射采样特征图像，通过f(r，θ)可以把三张特征图像视为一个整体来描述；
[0094][0095][0096][0097][0098][0099]
其中，re(g)表示复数的实部，im(g)表示复数的虚部，g
nms
(f1)、g
nms
(f2)和g
nms
(f3)分别为三张投射特征图的泛型极复指数(gpce)变换系数/矩，为qgpce变换系数。
[0100]
s4：对混沌置乱的特征图像和水印图像进行异或操作获得零水印图像。本步骤还
需要说明的是，本发明方法分为水印生成和水印验证两个阶段，在水印生成过程，基于dti图像的冠状面、矢状面和横切面进行光线投射获得三张正交投影特征图像，计算三张投影特征图的四元数极复指数变换，利用正交矩的幅值构造矩特征图像，将混沌置乱的矩特征图像和水印图像进行异或运算，生成密钥图像，包括：
[0101]
计算获得宿主dti图像f
d
的三张正交光线投射特征图f1，f2，f3；
[0102]
利用f1，f2，f3获得qgpce变换系数q，定义为三张投射特征图的正交矩，其矩容量为l＝(2n+1)(2m+1)；
[0103]
将伪随机序列作为密钥k1，根据给定的二值水印图像w＝{f
w
(i，j)|i∈[1，n
h
]，j∈[1，n
w
]∩n
h
×
n
w
≤l}，从q中选择n
h
×
n
w
个矩作为矩向量v
n
＝{v
i
|i∈[1，n
h
×
n
w
]}；
[0104]
根据矩向量v
m
计算幅值获得幅向量a
m
＝{a
i
|i∈[1，n
h
×
n
w
]}，将a
m
构造为二维矩矩阵，h＝{f
h
(i，j)|i∈[1，n
h
]，j∈[1，n
w
]}作为二维矩特征图像；
[0105]
对矩特征图像h使用logistic映射进行加密，如下，
[0106]
x
i+1
＝λx
i
(1
‑
x
i
)，i＝0，1，2，...
[0107]
其中，x
i
∈[0，1]，λ∈[0，4]为控制参数，令λ＝4，保证混沌系统在[0，1]之间的均匀映射，给定初始值x0作为密钥k2生成长度为n
h
×
n
w
的混沌序列l，再将其进行二值化获得二值混沌序列l
b
，t为给定阈值，令t＝0.5，如下，
[0108][0109]
利用异或操作，将l
b
对h
b
进行加密，获得加密矩特征图像h
l
，如下，
[0110][0111]
对混沌序列h
l
和二值水印图像w进行异或操作获得密钥图像k＝{f
k
(i，j)|i∈[1，n
h
]，j∈[1，n
w
]}，如下，
[0112][0113]
其中，表示异或操作，将(w，k1，k2，k)作为原始图像的验证密钥存储在第三方版权中心。
[0114]
水印验证是水印生成过程的逆过程，用于dti图像的版权验证，根据给定dti图像计算获得置乱的矩特征图像，将置乱的矩特征图像和给定的密钥图像进行异或运算，获得水印图像，进而完成版权验证和完整性验证，包括：
[0115]
计算提取待验证dti图像f
′
d
的三张正交光线投射特征图f
′1，f
′2，f
′3；
[0116]
利用f
′1，f
′2，f
′3获得qgpce变换系数q
′
；
[0117]
基于从版权方获取的密钥k1，从q
′
中选择n
h
×
n
w
个矩作为矩向量v
′
m
＝{v
′
i
|i∈[1，n
h
×
n
w
]}；
[0118]
根据矩向量v
′
m
计算幅值获得幅向量a
′
m
＝{a
′
i
|i∈[1，n
h
×
n
w
]}，将a
′
m
构造为二维矩矩阵，h
′
＝{h
′
i
(i，j)|i∈[1，n
h
]，j∈[1，n
w
]}作为二维矩特征图像；
[0119]
对矩特征图像h
′
进行logistic映射加密，使用从版权方获取的密钥k2作为初始值x0生成长度为2n
w
的混沌序列l
′
；
[0120]
将其进行二值化获得二值混沌序列l
′
b
，利用异或操作用l
′
b
对h
′
进行加密，获得加密矩特征图像h
′
l
；
[0121]
对混沌序列h
′
l
和从版权方获取的密钥图像k进行异或操作获得水印图像w
′
＝{f
′
w
(i，j)|i∈[1，n
h
]，j∈[1，n
w
]}，通过评价w
′
完成版权验证。
[0122]
实施例2
[0123]
本实施例采用数据为公开数据集oasis的脑部dti图像作为原始图像，分别对40例个体的dti图像进行了实验，同时，使用32*32的二值图像作为水印图像，利用一组测试图像来衡量算法对于各种攻击的鲁棒性，使用峰值信噪比(peak signal
‑
to
‑
noise ratio，psnr)来衡量受攻击图像的失真程度，psnr值越小，表明受攻击图像的失真程度大，即图像收到的攻击强度越高，psnr定义如下：
[0124][0125]
其中，max为图像的最大灰度阶数，mse为大小均为u
×
v的原始图像i与受攻击图像k的均方差，其定义如下：
[0126][0127]
利用比特正确率(bit correctness rates，bcr)来衡量算法的鲁棒性，bcr的定义如下：
[0128][0129]
其中，b
c
是正确检测到的水印比特位数，n
h
×
n
w
是水印图像的总比特位数，bcr∈[0，1]，bcr越高，提取的水印越接近原始水印，即鲁棒性越好。
[0130]
参照图4，噪声攻击是常见的图像攻击方式，在图像传输和转储过程中，经常会产生噪声污染，在这部分中，采用以dti二维横断面切片为单位，在图像数据中加入不同方差的全局高斯噪声和全局椒盐噪声来测试算法是否能有效地抵抗噪声攻击，图4展示了dti图像遭受不同参数的高斯噪声和椒盐噪声攻击后的横断面其中一层二维横断面切片，同时给出了遭受攻击后的psnr值。
[0131]
表1：噪声攻击下的bcr表。
[0132][0133]
参照表1，其总结了算法在不同攻击下的bcr值，结果显示在椒盐＝0.03时，bcr值依然保持1.000，当高斯＝0.03时，依然能够让bcr值保持在0.96以上。
[0134]
参照图5，为了测试算法对jpeg压缩的鲁棒性能，使用不同的质量因子q对以dti二维横断面切片为单位进行了jpeg全局压缩攻击，分别使用10，30，70，90作为q值，图5展示了dti图像遭受不同q值的jpeg压缩攻击后的横断面切片，同时给出了遭受攻击图像与原图像的psnr值。
[0135]
表2：旋转攻击下的bcr表。
[0136][0137]
参照表2，总结了在不同参数q攻击下的bcr值，随着jpeg压缩的质量因子q的提高，bcr值越来越接近于1，即使在q＝10的情况下，bcr值也能够保持在0.98以上。
[0138]
参照图6，图像滤波是常见的图像处理方式之一，通常应用于图像增强和去噪等方面，但同时会对图像原始数据造成一定破坏，在这部分实验以dti二维横断面切片为单位进行了中值滤波攻击和高斯滤波攻击，其中，中值滤波攻击采用了3*3，5*5和7*7三种不同尺寸的空域滤波器进行测试，高斯滤波攻击采用了参数1.0，1.5和2.0三种不同的参数值的低通滤波进行测试，根据图6的示意，展现了dti图像遭受不同参数的中值滤波和高斯低通滤波攻击后的横断面切片，同时给出了遭受攻击后的psnr值。
[0139]
表3：滤波攻击下的bcr表。
[0140][0141]
参照表3，给出了在不同攻击下的bcr值，当中值滤波器为7*7时，bcr值也能够保持在0.98以上；而在高斯低通滤波＝2.0，bcr依然可以保持为1.0000。
[0142]
参照图7，图像旋转对于dti图像是一种强烈的几何攻击，因为dti图像的张量元素具有方向表示，在图像旋转时不同时对张量进行旋转会造成张量方向与解剖结构方向的不一致，会直接导致dti图像失去医学和研究价值，本实施例为了验证算法对于旋转攻击的鲁棒能力，分别设置了axial单轴为旋转轴的5度，15度，30度，45度攻击，同时不进行张量元素的同步旋转，dti图像遭受不同参数单轴旋转攻击后的横断面切片其中一层二维图像，同时给出了遭受攻击后的psnr值。
[0143]
表4：旋转攻击下的bcr表。
[0144][0145]
参照表4，总结了在旋转攻击下水印图的bcr值，当旋转角度为15
°
时，依然能够保持1.0000的bcr值，即使旋转攻击的角度扩大到45
°
，也可以保持0.92以上的bcr值。
[0146]
参照图8，图像缩放是对图像进行下采样或者上采样，下采样会造成图像信息缺失，上采样会造成图像信息冗余，对水印提取造成影响，本实施例测试所提出算法针对dti图像的三维缩放攻击的抵抗能力，使用一定的缩放因子对图像进行了三维缩放，分别以基于原图像尺寸的25％，50％，75％，125％，150％，200％的因子来处理图像，再将dti图像进
行再缩放，恢复到原始图像尺寸，dti图像遭受不同参数的三维缩放攻击后的横断面切片，同时给出了遭受攻击后的psnr值。
[0147]
表5：缩放攻击下的bcr表。
[0148][0149]
参照表5，总结了在不同缩放因子的攻击下水印图的bcr值，除了由于缩放因子为25％的攻击下导致的大部分图像信息丢失，导致bcr值低于0.90，对于缩放因子为50％极其以上的攻击，bcr值均为1.000。
[0150]
参照图9，图像裁剪是最常见的一种几何攻击方式，直接对图像进行裁剪，去除图像中的部分信息，从而造成了图像信息缺失，而大面积的裁剪会造成水印特征提取困难，进而直接影像水印质量，这部分实验对图像进行了不同程度的裁剪攻击，以dti二维横断面切片进行以边长1/8、1/4和1/2的左上角裁剪，也就是说，在tdf上，就是1/16、1/8和1/4三维体积裁剪，图9展示了dti图像裁剪攻击后的横断面其中一层二维横断面切片，同时给出了遭受攻击后的psnr值。
[0151]
表6：左上角裁剪攻击下的bcr表。
[0152]
攻击裁剪1/8裁剪1/4裁剪1/2bcr1.00001.00000.9795
[0153]
参照表6，总结了在不同的攻击下提取的水印的bcr值，1/8和1/4裁剪的攻击，bcr值均为1，1/2的裁剪虽然导致了大量的信息确实，但bcr值仍然能够保持在0.97以上。
[0154]
考虑到图像在实际的传输过程中易受到多重攻击，因此在这部分通过对图像施加多重攻击，进一步测试了算法针对多重攻击的鲁棒性，多重攻击依然是基于dti图像二维横断面切片施加的攻击，攻击1,攻击2,攻击3分别为多重攻击中每部分攻击的单独bcr值，多重表示在多重攻击下的bcr值，可以看出在不同参数的多重攻击下，依然能使bcr值达到0.95以上。
[0155]
表7：多重攻击下的bcr表。
[0156]
[0157][0158]
为了证明本实施例提出的算法方案的优越性，分别与3种优秀的二维图像零水印方案进行了对比。
[0159]
表8：本发明方法与基于极复指数变换和逻辑映射的零水印算法，基于三元径向傅里叶矩的零水印算法和基于混合投票和混合加密的彩色图像零水印算法进行了鲁棒性(bcr)对比。
[0160][0161]
参照表8，给出了算法对比结果，除了高斯噪声攻击结果并非最优，本发明方法在面对其他攻击均表现出了最好的结果，部分攻击下甚至能够保持bcr值为1.0000，表明了算法也在大部分攻击下的极其优秀的鲁棒性。
[0162]
应说明的是，以上实施例仅用以说明本发明的技术方案而非限制，尽管参照较佳实施例对本发明进行了详细说明，本领域的普通技术人员应当理解，可以对本发明的技术方案进行修改或者等同替换，而不脱离本发明技术方案的精神和范围，其均应涵盖在本发
明的权利要求范围当中。