外积累加求解三角矩阵与矩阵内积的方法与流程

1.本发明属于计算机应用技术领域，尤其涉及一种外积累加求解三角矩阵与矩阵内积的方法。


背景技术：

2.在数学上，矩阵是指纵横排列的二维数据表格，最早来自于方程组的系数及常数所构成的方阵。矩阵内积乘法是数值计算、机器学习、工程模拟等众多领域算法的基础。
3.目前，在现有的矩阵内积乘法计算中，最经常涉及到的矩阵就是上三角矩阵、下三角矩阵、三角矩阵以及稠密矩阵，其中，上三角矩阵和下三角矩阵为主对角线以下或以上都是零的方阵，这部分零元素是可以不参与计算依然保证运算结果的正确性，同时对于零元素可以直接放弃存储来提升内存的利用效率。
4.但是在计算和存储的过程中对三角矩阵a之中零元素的忽略导致内存访问的不连续，不利于利用现代处理器架构中的各级高速缓存。因而涉及三角矩阵和其他矩阵的外积计算中，三角矩阵中的零元素参与了外积计算，这种计算其不仅降低了外积运算的计算效率也增加了外积计算后零值向内存写入的需求，进而减少了内存写入的有效带宽。


技术实现要素：

5.本发明针对上述的外积累加求解三角矩阵与矩阵内积时所存在的零元素必须要参与计算的技术问题，提出一种方法简单、操作方便且能够在零元素不参与计算的情况下，保证内存访问连续性的外积累加求解三角矩阵与矩阵内积的方法。
6.为了达到上述目的，本发明采用的技术方案为，本发明提供一种外积累加求解三角矩阵与矩阵内积的方法，包括以下有效步骤：
7.a、首先对三角矩阵与矩阵的原始数据的完成读取；
8.b、对三角矩阵进行数据压缩，将二维布局的三角矩阵压缩为一维布局的压缩三角矩阵；
9.c、读取压缩三角矩阵第i列以及读取矩阵中第i行外积运算生成ci；
10.d、对所得到的外积结果进行累加，即可得到三角矩阵与矩阵内积；
11.其中，所述b步骤，三角矩阵按照下述方案进行压缩：
12.b1、首先构件2*2大小的元素方块；
13.b2、以三角矩阵的主对角线为起点，将元素方块内的数字以列的顺序依次记录形成一维布局，即可得到一维布局的压缩三角矩阵。
14.作为优选，还包括e步骤，e、判断是否完成到三角矩阵的最后一列，如果是，则完成计算；如果否，则i自增1，重复c～e步骤。
15.作为优选，所述压缩三角矩阵还包括压缩后总长组，所述压缩后总长组为x＝m*(m+1)/2，其中，x为压缩后成一维布局的非零元素的总个数，m为三角矩阵的列数。
16.与现有技术相比，本发明的优点和积极效果在于，
17.1、本发明提供一种外积累加求解三角矩阵与矩阵内积，根据三角矩阵的特性，采用元素方块压缩的方式将将原有的二维布局的三角矩阵压缩为一维布局的压缩三角矩阵，除去了三角矩阵的零元素值，进而避免了无效数值的计算，达到节省内存访问和无效运算的目的，从而提高了运算效率，为数值计算、机器学习、工程模拟相关技术的快速运算提供保障。
附图说明
18.为了更清楚地说明本发明实施例的技术方案，下面将对实施例描述中所需要使用的附图作一简单地介绍，显而易见地，下面描述中的附图是本发明的一些实施例，对于本领域普通技术人员来讲，在不付出创造性劳动性的前提下，还可以根据这些附图获得其他的附图。
19.图1为上三角矩阵依据元素方块压缩存储方式存储的转换过程；
20.图2为上三角矩阵依据元素方块压缩存储方式存储的其他元素方块的转换过程；
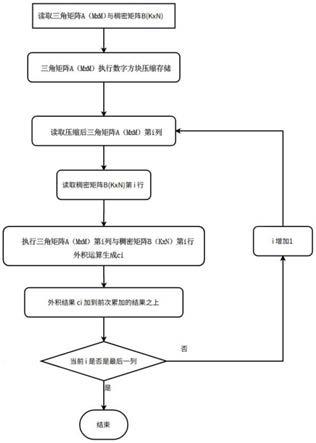
21.图3为上三角矩阵与稠密矩阵外积累加流程图。
具体实施方式
22.为了能够更清楚地理解本发明的上述目的、特征和优点，下面结合附图和实施例对本发明做进一步说明。需要说明的是，在不冲突的情况下，本申请的实施例及实施例中的特征可以相互组合。
23.在下面的描述中阐述了很多具体细节以便于充分理解本发明，但是，本发明还可以采用不同于在此描述的其他方式来实施，因此，本发明并不限于下面公开说明书的具体实施例的限制。
24.首先说明，本案所提供的方案适用于任何三角矩阵的外积累加求解的方法，如：
25.外积方法求解上三角矩阵a(mxm)与稠密矩阵b(mxk)的内积结果c(mxk)
26.外积方法求解上三角矩阵a(mxm)与三角矩阵b(mxk)的内积结果c(mxk)
27.外积方法求解上三角矩阵a(mxm)与上三角矩阵b(mxm)的内积结果c(mxm)
28.外积方法求解上三角矩阵a(mxm)与下三角矩阵b(mxm)的内积结果c(mxm)
29.外积方法求解稠密矩阵a(mxk)与上三角矩阵b(kxk)的内积结果c(mxk)
30.外积方法求解三角矩阵a(mxk)与上三角矩阵b(kxk)的内积结果c(mxk)
31.外积方法求解下三角矩阵a(mxm)与稠密矩阵b(mxk)的内积结果c(mxk)
32.外积方法求解下三角矩阵a(mxm)与三角矩阵b(mxk)的内积结果c(mxk)
33.外积方法求解下三角矩阵a(mxm)与上三角矩阵b(mxm)的内积结果c(mxm)
34.外积方法求解下三角矩阵a(mxm)与下三角矩阵b(mxm)的内积结果c(mxm)
35.外积方法求解稠密矩阵a(mxk)与下三角矩阵b(kxk)的内积结果c(mxk)
36.外积方法求解三角矩阵a(mxk)与下三角矩阵b(kxk)的内积结果c(mxk)
37.在本实施例中，以外积方法求解上三角矩阵a(4x4)与稠密矩阵b(4x3)的内积结果c(mxk)进行举例
38.实施例1，在本实施例中，假设上三角矩阵a(4x4)为：
[0039][0040]
稠密矩阵b(4x3)为：
[0041]
首先，完成对上三角矩阵a(4x4)和稠密矩阵b(4x3)的数据进行读取，根据主对角线以下都是零的方阵称为上三角矩阵定义可以知道，如果构件一个2x2的元素方块，那么在上三角矩阵中主对角线上的元素方块，左下元素总是零，非对角线上的块：要么全是零，要么全是非零，当然，在下三角矩阵中，则是主对角线右上角的元素，总是零，那么，对块进行压缩时，按照块就可以将二维的三角矩阵转换为一维的压缩矩阵，在压缩过程中，可以以列的顺序依次记录形成一维布局，也可以以行的顺序依次记录呈一维数据，比如，第一元素方块有三个元素，其属于第一列和第二列，第二元素方块中，其就含有四个元素，其按照顺序属于第三列和第四列，而第三个元素方块中，其就含有三个元素，其按照顺序属于第三列和第四列，根据形成的一维元素，就可以根据第几个元素，推断出其在原三角矩阵所在的位置，在本实施例中，将所形成的一维元素数组命名为压缩元素值数组，为了更为准确的反向推断出原三角矩阵，在本实施例中，所形成的压缩三维矩阵中还增加有压缩后总长组，压缩后总长为压缩元素值数组的元素的个数，压缩后总长组的数字为x＝m*(m+1)/2，其中，x为压缩后成一维布局的非零元素的总个数，m为三角矩阵的列数，这样，可以根据x的数值，进一步确保反推后的原三角矩阵的位置，这样，就避免了内存访问的不连续的问题。
[0042]
列向压缩以后的三角矩阵a(4x4)与稠密矩阵b(4x3)再依据外积累加方法求解矩阵内积的过程。首先依据行索引数组计算出三角矩阵a(4x4)第一列的所有非零元素在非零元素值数组中的位置，然后读取相应范围的数据与稠密矩阵b(4x3)第一行执行外积运算。同样地，计算出三角矩阵a(4x4)第二列的所有非零元素在非零元素值数组中的位置，与稠密矩阵b(4x3)第二行再次执行外积运算。依次执行三角矩阵a(4x4)压缩后的第i列与密矩阵b(4x3)第i行外积运算。
[0043]
将所有数据计算后，进行外积累加，即可得到上三角矩阵a(4x4)和稠密矩阵b(4x3)的内积。
[0044]
最后，针对矩阵数量较多的三角矩阵a(mxk)与稠密矩阵b(kxn)可以描述成如图3所示，具体的说，首先由模块完成三角矩阵a(mxk)与稠密矩阵b(kxn)原始数据的读取。模块执行三角矩阵a(mxk)的列向数据压缩，下面执行外积计算，分别由模块读取列向压缩的三角矩阵a(mxk)第i列以及模块读取稠密矩阵稠密矩阵b(kxn)第i行生成ci。再由完成外积累加过程，累加一般是在同一块内存空间之中反复累加，将当前结果叠加到该内存空间的值之上。最后判断是否完成到三角矩阵a(mxk)的最后一列。如果是，则完成计算；如果否，则i自增1，依次执行模块。
[0045]
需要说明是，针对其他不同组合的矩阵，也可以按照相同的方式来进行操作，以达
到压缩的目的。
[0046]
以上所述，仅是本发明的较佳实施例而已，并非是对本发明作其它形式的限制，任何熟悉本专业的技术人员可能利用上述揭示的技术内容加以变更或改型为等同变化的等效实施例应用于其它领域，但是凡是未脱离本发明技术方案内容，依据本发明的技术实质对以上实施例所作的任何简单修改、等同变化与改型，仍属于本发明技术方案的保护范围。