一种暖通设备运行策略辨识方法

本发明涉及建筑能源管理领域，更具体地，涉及一种暖通设备运行策略辨识方法。

背景技术：

融合建筑数据与智能数据算法的应用与创新主要集中于提高建筑环境舒适度和降低建筑运行能耗两方面，如何合理制定和调节设备运行策略以维持建筑环境和运行能耗的平衡成为主要的研究点。对于bas系统数据的研究集中在对建筑设备内部数据的使用，对bas数据中各数据的关联性的研究和讨论和建筑负荷或者能耗的预测，这些研究与应用通过提高设备效率、诊断设备故障和改造系统形式来间接地提高建筑环境舒适度或降低建筑能耗。

然而，诊断设备的优化方法需要多种维度的建筑数据，由于不同建筑的设备参数均有不同或缺失，目前，相关方法都有可能产生低鲁棒性和低精度的结果，改造系统形式的优化方法导致了改造成本较高。

因此，现有技术中亟需一种借现有的建筑数据，以数学的方法研究暖通运行设备与设备组的识别并识别当前的暖通运行策略，以期融合智能数据算法的技术手段，来指导提高建筑环境舒适度和改善建筑运行效果的技术方案。

技术实现要素：

针对上述问题，本发明提出一种暖通设备运行策略辨识方法。

本发明为解决上述技术问题采用的技术方案如下：

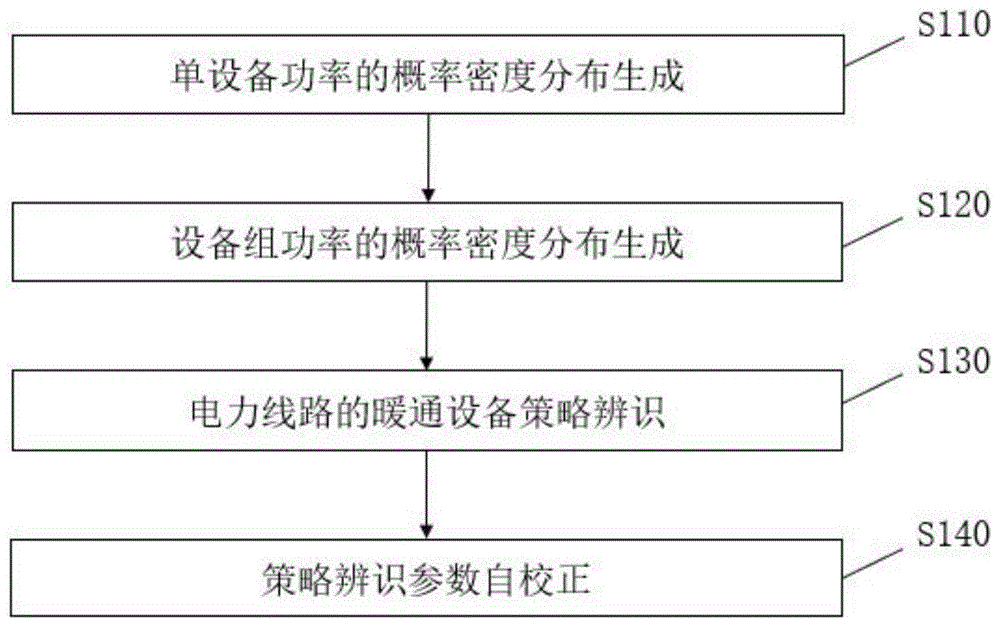
一种暖通设备运行策略辨识方法，包括以下步骤：

s110、生成单设备功率的概率密度分布；

s120、生成设备组功率的概率密度分布；

s130、辨识电力线路的暖通设备策略；

s140、策略辨识参数自校正。

步骤s110中，单设备功率包括定频设备功率和变频设备功率；

定频设备功率的概率密度分布函数采用高斯分布；

变频设备包括类定频设备和非类定频设备；

其中，类定频设备功率的概率密度分布函数也采用高斯分布；非类定频设备功率的概率密度分布采用统计学的方法，通过统计一定时间内功率的实际分布情况，以获得统计学的设备功率的概率密度分布函数。

步骤s120包括以下子步骤：

s121、计算设备组：

计算所有可能的设备开启组合，其中，对于包含n个不同设备的设备组，理论上拥有2ⁿ种不同的设备开启组合；

s122、计算每个设备组的概率密度分布：

对于包含n个不同设备的设备组，设备n的开启功率概率密度分布函数记为pn(x)，该设备组的概率密度分布函数记为p1,2,3…(x)，其中，1，2，3，…，n表示该设备组中处于开启状态的设备1、设备2、设备3、…、设备n；p表示概率密度函数，x表示给定的功率值；

该设备组的功率由当前处于开启状态的设备的功率累加而成，该设备组的功率的概率密度计算方式如下：

其中，x1+x2+x3+...+xn＝x；

s123、卷积计算：

将该设备组分解为包含2个设备的设备开启组合和包含n-2个设备的设备开启组合；其中，包含2个设备的设备开启组合的概率密度计算方式如下：

将包含2个设备的设备开启组合视为1个新的设备，于是，包含n个设备的设备开启组合转换为包含n-2+1个设备的设备开启组合，通过卷积操作，将包含n个设备的设备开启组合的功率的概率密度计算转化为包含n-1个设备的设备开启组合的功率的概率密度计算；重复进行卷积操作，实现n个设备组合的功率的概率密度计算；对于包含n个设备的设备开启组合，需要n-1次的卷积操作；

s124、计算设备组的功率的概率密度函数：

对于2ⁿ种不同的设备开启组合分别进行多重卷积计算，得到设备组的功率的概率密度函数。

步骤s130采用贝叶斯判别方法：

设每一种设备开启组合用c表示，ci表示第i种设备组合方式，对于包含n种不同设备的设备组，共有2ⁿ种设备开启组合，c1,c2,c3,…,c2ⁿ表示第1,2,3,…2ⁿ种设备开启组合，给定x表示设备组的特定功率值，预测x属于在条件x下具有最大后验概率的类，采用贝叶斯分类法预测x属于类ci，当且仅当：

p(ci|x)＞p(cj|x)1≤i,j≤2ⁿ,i≠j

最大化p(ci|x)，p(ci|x)最大的类ci称为最大后验假设，根据贝叶斯定理：

p(x)对于所有类为常数，仅需p(x|ci)p(ci)最大化即可，如果所有类的先验概率未知，则假定这些类是等概率的，即p(c1)＝p(c2)＝…＝p(c2ⁿ)；否则最大化p(x|ci)p(ci)。

步骤s140包括以下子步骤：

s141：给定某一设备组的额定功率；

s142：根据该设备组功率的概率密度分布得到概率最大的设备开启组合；

s143：重新计算该设备开启组合的功率；

s144：判断步骤s143计算得到的该设备开启组合的功率是否等于步骤s141中给定的设备组的额定功率，如果不等于，则回到步骤s141，重新给定该设备组的额定功率，同时校正该设备组的额定功率；如果等于，则进行步骤s145；

s145：校正该设备组的高斯分布参数。

步骤s141包括：假定设备组功率的期望μ为设备额定功率，假定标准差δ为额定功率的10％。

步骤s144包括：利用多重卷积计算各个设备组合的概率分布，最终得到给定功率xm×1下设备的启停矩阵bm×n，其中，xm×1表示m个实际的线路功率值，可视为不同时刻的线路功率，bm×n表示与m个实际的线路功率值对应的n台线路设备启停情况；校正设备组的额定功率通过下式进行计算：

p'＝b^-1x

其中b^-1为b的伪逆，即使用最小二乘法计算满足功率和为x的设备功率参数p；当校正计算的功率参数p'与给定的额定功率参数p之差小于迭代计算要求的最小值时，则当前给定的额定功率参数p与实际功率近似相等，即判定步骤s143计算得到的该设备开启组合的功率为该设备组的额定功率；当两者相差较多时，则以p'作为步骤s141中初始给定的设备组额定功率，继续进行策略辨识自校正计算流程。

本发明与现有技术相比的有益效果是：

1.设计常见设备的典型概率密度分布模型，使用卷积计算多设备构成的设备组功率的概率密度分布，在现有电力监控平台在单条线路下具有多个设备的情况下，解决暖通设备的运行策略辨识问题。

2.策略辨识参数自校正方法可以在给定初始设备功率参数组的情况下，通过迭代更新的方法寻找满足实际电力消耗表现的设备功率参数组，从而提高设备运行策略辨识效果。

附图说明

图1为暖通设备运行策略辨识方法原理框架图。

图2为暖通设备运行策略辨识方法的步骤s120的流程示意图。

图3为暖通设备运行策略辨识方法的步骤s140的流程示意图。

具体实施方式

下面结合具体实施例，对本发明的技术方案进行清楚完整的描述及说明，但并不以此作为本申请保护范围的限定。

如图1-3所示的暖通设备运行策略辨识方法，包括以下步骤：

s110、生成单设备功率的概率密度分布；

s120、生成设备组功率的概率密度分布；

s130、辨识电力线路的暖通设备策略；

s140、策略辨识参数自校正。

步骤s110中，单设备功率包括定频设备功率和变频设备功率；

定频设备功率的概率密度分布函数采用高斯分布；

变频设备包括类定频设备和非类定频设备；

其中，类定频设备功率的概率密度分布函数也采用高斯分布；非类定频设备功率的概率密度分布采用统计学的方法，通过统计一定时间内功率的实际分布情况，以获得统计学的设备功率的概率密度分布函数。

高斯分布的表达式如下：

其中，μ为设备的平均功率值，σ为标准差。

变频设备中，变频水泵频率被被人为设定为45～47hz的变频设备，拥有类似定频设备的性质，上述变频设备即为“类定频设备”，同样适用高斯分布。

其他变频设备为非类定频设备，非类定频设备功率的概率密度分布采用统计学的方法，通过统计一定时间内功率的实际分布情况，以获得统计学的设备功率概率密度分布函数。但是，对于非类定频设备准确按照设备开启时的功率表运行的情况，非类定频设备功率的概率密度通过高斯分布来拟合实际分布曲线。

步骤s120包括以下子步骤：

s121、计算设备组：

计算所有可能的设备开启组合，其中，对于包含n个不同设备的设备组，理论上拥有2ⁿ种不同的设备开启组合；

s122、计算每个设备组的概率密度分布：

对于包含n个不同设备的设备组，设备n的开启功率概率密度分布函数记为pn(x)，该设备组的概率密度分布函数记为p1,2,3…(x)，其中，1，2，3，…，n表示该设备组中处于开启状态的设备1、设备2、设备3、…、设备n；p表示概率密度函数，x表示给定的功率值；

该设备组的功率由当前处于开启状态的设备的功率累加而成，该设备组的功率的概率密度计算方式如下：

其中，x1+x2+x3+...+xn＝x；

s123、卷积计算：

将该设备组分解为包含2个设备的设备开启组合和包含n-2个设备的设备开启组合；其中，包含2个设备的设备开启组合的概率密度计算方式如下：

将包含2个设备的设备开启组合视为1个新的设备，于是，包含n个设备的设备开启组合转换为包含n-2+1个设备的设备开启组合，通过卷积操作，将包含n个设备的设备开启组合的功率的概率密度计算转化为包含n-1个设备的设备开启组合的功率的概率密度计算；重复进行卷积操作，实现n个设备组合的功率的概率密度计算；对于包含n个设备的设备开启组合，需要n-1次的卷积操作；

s124、计算设备组的功率的概率密度函数：

对于2ⁿ种不同的设备开启组合分别进行多重卷积计算，得到设备组的功率的概率密度函数。

其中，当设备组为空时，显然空组合的概率密度分布如下式所示：

但可能线路存在一些干扰源导致在已知设备全关的情况下仍存在少量电能消耗，为了提高计算流程的稳定性，可将空组合的概率密度分布设置为0附近的平均概率密度分布。

步骤s130采用贝叶斯判别方法：

设每一种设备开启组合用c表示，ci表示第i种设备组合方式，对于包含n种不同设备的设备组，共有2ⁿ种设备开启组合，c1,c2,c3,…,c2ⁿ表示第1,2,3,…2ⁿ种设备开启组合，给定x表示设备组的特定功率值，预测x属于在条件x下具有最大后验概率的类，采用贝叶斯分类法预测x属于类ci，当且仅当：

p(ci|x)＞p(cj|x)1≤i,j≤2ⁿ,i≠j

最大化p(ci|x)，p(ci|x)最大的类ci称为最大后验假设，根据贝叶斯定理：

p(x)对于所有类为常数，仅需p(x|ci)p(ci)最大化即可，如果所有类的先验概率未知，则假定这些类是等概率的，即p(c1)＝p(c2)＝…＝p(c2ⁿ)；否则最大化p(x|ci)p(ci)。

步骤s140包括以下子步骤：

s141：给定某一设备组的额定功率。步骤s141还包括：假定设备组功率的期望μ为设备额定功率，假定标准差σ为额定功率的10％。

s142：根据该设备组功率的概率密度分布得到概率最大的设备开启组合。

s143：重新计算该设备开启组合的功率。

s144：判断步骤s143计算得到的该设备开启组合的功率是否等于步骤s141中给定的设备组的额定功率，如果不等于，则回到步骤s141，重新给定该设备组的额定功率，同时校正该设备组的额定功率；如果等于，则进行步骤s145。

步骤s144包括：利用多重卷积计算各个设备组合的概率分布，最终得到给定功率xm×1下设备的启停矩阵bm×n，其中，xm×1表示m个实际的线路功率值，可视为不同时刻的线路功率，bm×n表示与m个实际的线路功率值对应的n台线路设备启停情况；校正设备组的额定功率通过下式进行计算：

p'＝b^-1x

其中b^-1为b的伪逆，即使用最小二乘法计算满足功率和为x的设备功率参数p；当校正计算的功率参数p'与给定的额定功率参数p之差小于迭代计算要求的最小值时，则当前给定的额定功率参数p与实际功率近似相等，即判定步骤s143计算得到的该设备开启组合的功率为该设备组的额定功率；当两者相差较多时，则以p'作为步骤s141中初始给定的设备组额定功率，继续进行策略辨识自校正计算流程。

s145：校正该设备组的高斯分布参数，高斯分布参数包括设备组功率的期望μ和标准差σ。

其中，期望μ和标准差σ这两个参数在步骤s110中，作为高斯分布的参数，得到单设备功率的概率密度分布函数；再步骤s120的卷积计算，得到设备组功率的概率密度分布函数。这样经过设备的概率分布模型的选取和参数的设定，可以得到初步的暖通设备组的策略辨识结果。

校正计算流程的目的在于使得校正功率的概率分布贴近于实际功率的分布，从而为策略辨识提供更加准确的基础信息，使得辨识设备启停策略更加准确，自校正方法的建立也是基于迭代循环和最小二乘法寻找最优参数的思想。

相似的标号和字母在下面的附图中表示类似项，因此，一旦某一项在一个附图中被定义，则在随后的附图中不需要对其进行进一步定义和解释。同时，在本申请的描述中，术语“第一”、“第二”等仅用于区分描述，而不能理解为指示或暗示相对重要性。

以上所述的仅是本发明的优选实施方式，但本发明并不局限于上述的具体实施方式，对于本领域的普通技术人员来说，在不脱离本发明创造构思的前提下，还可以做出若干变形和改进，这些都属于本发明的保护范围。