一种基于物联网技术的物流车辆智能调度算法

本发明涉及物联网技术与智能运算领域，具体涉及到一种基于物联网技术的物流车辆智能调度算法。

背景技术：

近些年来，我国经济快速发展，国内物流行业面临着际遇的同时也伴随着压力，日益膨胀的用户需求促使着物流运输行业积极寻求技术革新。智慧物流要求以物流车辆个体为基础信息单元，拓展信息交互形式、改善道路交通通行状况、提高公共交通资源利用率，进一步实现物流公司对物流车辆更有效率的管理，将物联网技术切实的应用到物流产业之中。同时，随着车联网技术不断融入物流行业，如何以合理的方式给出最适合物流运输实际情况的调度方案，已成为物流公司迫切期待解决的问题。

近年来，物联网以及云端计算技术的不断进步，使得物流管理更加信息化和系统化。信息数据化的物流站点、仓库、货物以及物流车辆信息，令智能调度的实现成为可能。但是以往的调度算法因为缺少完整体系的数据进行支持，大多采用物流车辆装配和物流车辆行驶路线分别考虑的思路进行设计，所给出的调度方案往往缺乏整体性考虑。随着物联网技术以及物流公司数据库的不断完善，为满足物流公司对合理调度方案的需求，建立一种将物流车辆货物装配及物流车辆路线规划作为整体考虑的物流调度数学模型，并根据所建立模型，提出一种基于物联网技术的物流车辆智能调度算法，以达到降低物流运输成本、提高物流运输效率的目的。

技术实现要素：

为了实现上述发明目的，本发明采用了一种基于物联网技术的物流车辆智能调度算法，技术方案如下：

1、物流车辆智能调度模型。

(1)物流车辆智能调度模型的建立。

目前，国内大部分城市的物流配送中心通常采用辐射式选址的方式，即以地区配送中心为中点，向外围地区发散，并设有集散式配送点。因而大部分物流调度算法通常将问题归纳为一个核心和多个发散点的模型。但随着智慧物流产业的发展，辐射式模型效率较低的弊端也逐渐显现，派出的车辆每次只为一个集散站点进行货物运输的效率十分低下，在车辆未满载的情况下物流车辆可以前往多个集散站点进行装载作业后再返回配送中心。因此，本文所设计的调度算法基于传统辐射模型加以优化，抽象出网状结构模型。其中，各集散中心节点间的道路也是连通的，物流车辆可为多个集散中心进行货物运输后再到达配送中心。

根据所设计模型，将物流运输中的对象抽象为以下集合：物流物品为g；配送点以及运输目的地为w；物流车辆为v；道路为l；调度方案的集合为s，调度方案分为每辆车辆的计划运输的货物以及路线规划。

(2)物流车辆智能调度模型的优化目标。

在建立调度模型的基础上，需要对本模型的约束条件和求解目标进行确定。首先，算法的优化目标为对于给定的物流车辆装配以及行驶路径调度方案，可以使整个物流过程具有最低的物流运输成本和最快的物流运输速度，同时也要保证物流货物的准时送达。其中，物流运输成本方面主要分为道路成本、储存成本、装卸成本三个方面。根据实际情况，将物流车辆运输消耗、平均装卸成本、物流仓库仓储所需成本、仓储平衡度、所装载货物需要送达剩余时间进行数据化处理，并将它们设置为优化目标。

2、物流车辆智能调度算法。

随着物联网技术的不断发展，各物流公司的站点仓库、货物信息、物流车辆数据库已趋于完善，本调度模型所使用的运算参数从物联网技术和物流公司信息数据库获得，包括物流车辆载重、位置信息，货物体积、剩余配送时间等，采用多目标优化算法，根据上文中所建立的调度模型和提出的优化目标进行求解，从而给出每辆物流车辆最佳的运输路线方案。算法基于多目标优化遗传算法进行设计，通过建立初始种群，经过交叉、变异，并按照上文所设计的优化目标进行择优选择，经过多次算法迭代后，得到更适合物流运输情况的调度方案。

附图说明

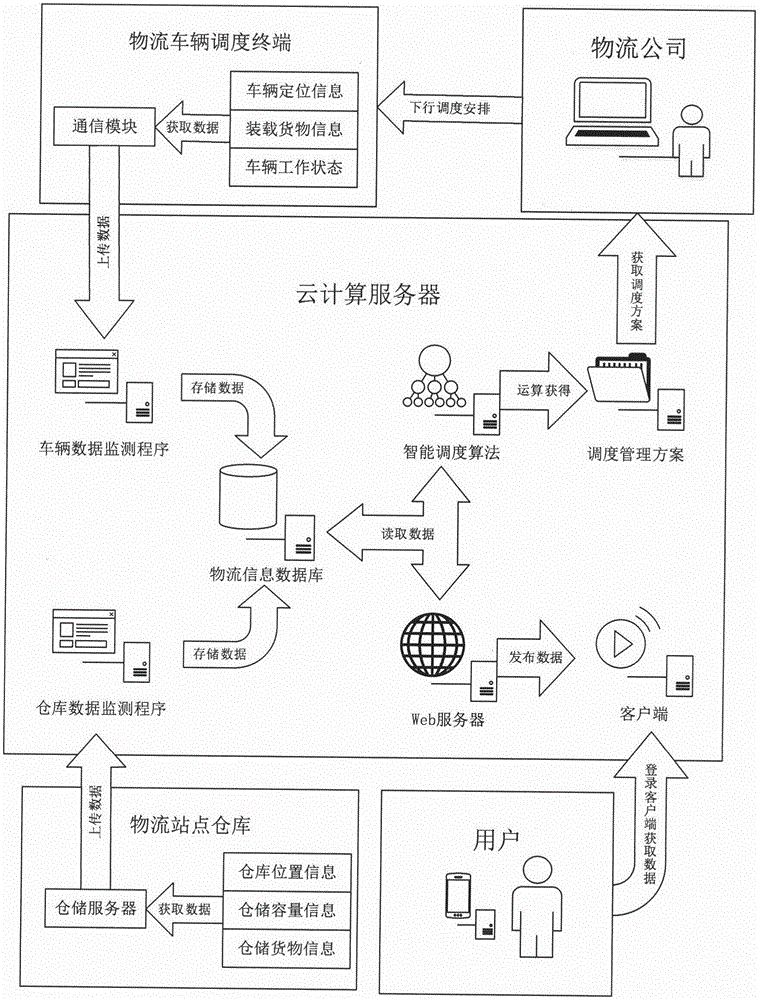
图1是本发明的物流调度系统模型图。

图2是本发明的物流节点抽象模型。

图3是本发明的物流车辆智能调度算法总体架构。

图4是本发明的基于遍历的最短路径算法。

图5是本发明的智能调度算法实现步骤。

具体实施方式

如图1所示，本发明是一种基于物联网技术的物流车辆智能调度算法，具体包括：

1、物流车辆智能调度模型。

(1)物流车辆智能调度模型的建立。

目前，国内大部分城市的物流配送中心通常采用辐射式选址的方式，即以地区配送中心为中点，向外围地区发散，并设有集散式配送点。因而大部分物流调度算法通常将问题归纳为一个核心和多个发散点的模型，如图2中的辐射中心结构所示。但随着智慧物流产业的发展，辐射式模型效率较低的弊端也逐渐显现，派出的车辆每次只为一个集散站点进行货物运输的效率十分低下，在车辆未满载的情况下物流车辆可以前往多个集散站点进行装载作业后再返回配送中心。因此，本文所设计的调度算法基于传统辐射模型加以优化，抽象出如图2中的网状结构模型。其中，各集散中心节点间的道路也是连通的，物流车辆可为多个集散中心进行货物运输后再到达配送中心。

根据所设计模型，将物流运输中的对象抽象为以下集合：物流物品为g；配送点以及运输目的地为w；物流车辆为v；道路为l；调度方案的集合为s，调度方案分为每辆车辆的计划运输的货物以及路线规划。各个集合的说明如下：

定义g表示物流货物，包括id，wt，ds，tm四个元素。其中，id表示物流货物的编号，通过ij进行表示，i表示货物仓库编号，j表示货物发往目的地仓库编号，wt表示货物的重量，ds表示货物所发往的目的地，tm表示货物达到所剩余的时间。

定义w表示配送中心和集散站点。设模型中只有一个配送中心w，包括id、cp两个元素。其中，id表示配送中心的编号，使用自然数1来表示，cp表示仓库容量，单位为t。设模型中有n-1个集散站点w2，w3，…wn，每一个wi包括id、cp两个元素。其中，id表示集散中心的编号，使用自然数2，3，…n来表示，cp表示仓库容量，单位为t。进一步来说，因为配送中心和集散站点属性相同，也可使用wi表示w。需要注意的是，当配送中心将物流货物发往各集散站点，通过集散站点将货物派送至用户手中；同时集散站点从用户手中收取到物流货物，统一运送到配送中心进行分拣，本地货物发送至指定集散站点，外地货物通过城际物流发送至其他配送中心。因此，模型中配送中心货物的目的地可以是集散站点中的任意一个，集散站点货物的目的地只能是配送中心w1。

定义v表示物流车辆，设模型中有m辆物流车辆v1，v2，…vm，每一个vi包括id、tl、rl、st、lc、pt六个元素。其中，id表示物流车辆的编号，使用自然数1，2，…m表示，tl表示物流车辆总载重量，rl表示物流车辆剩余载重量，st表示车辆当前状态，分为运输和等待两种状态，lc表示车辆当前位置，pt表示车辆调度路径。

定义l表示路网集合，设lij表示从仓库i到仓库j所需的运输成本，在实际应用中可以为此段路径的运输时间、运输距离，是否包含过桥过路费用等。

(2)物流车辆智能调度模型的优化目标。

在建立调度模型的基础上，需要对本模型的约束条件和求解目标进行确定。首先，算法的优化目标为对于给定的物流车辆装配以及行驶路径调度方案，可以使整个物流过程具有最低的物流运输成本和最快的物流运输速度，同时也要保证物流货物的准时送达。其中，物流运输成本方面主要分为道路成本、储存成本、装卸成本三个方面。定义s表示调度方案，使用形式化语言进行描述可表示为：

get：s(sh1，sh2，…shk)(1)

其中，k≤m(物流车辆总数)，shi表示物流车辆的调度状态，包括id、ld、lc、pt四个元素，可表示为：

shi(id，ld，lc，pt)(2)

id表示物流车辆的编号，ld表示物流车辆运输货物的集合，设物流车辆装载有ld1，ld2，…ldn的货物，ldi表示目的地为ji的货物，lc表示物流车辆定位信息，pt表示物流车辆所行驶路径的集合，使用pt1，pt2，…ptn表示路径节点。

设调度方案s有如下公式：

minf(x)＝[tr(s)，lu(s)，cc(s)，cb(s)，lt(s)]^t(3)

公式(3)中tr(s)表示物流车辆运输消耗，本文采取车辆运输耗时作为考虑，实际使用中还需根据情况进行选择。

其中，price(shi)表示在调度方案shi和lc确定时，通过最短路径法将物流车辆完成运送所产生的成本，tv表示方案中shi的运输货物总数。

公式(3)中lu(s)表示物流车辆的平均装卸成本。在实际的物流业务过程中，车辆是否满载对物流车辆的装卸成本影响较小，因此本文设计根据调度方案s中装卸行为的总次数进行计算。

其中，k表示装载行为次数，lp表示物流车辆单次装载所需成本，ul(shi)表示方案shi中卸货次数，lu表示物流车辆单次卸货成本。

公式(3)中cc(s)表示物流仓库存储所需成本。cc(s)约束的目的在于在调度中使物流车辆装载尽可能多的货物，以降低货物存储成本。

其中，cp表示每吨货物仓库的存储成本，vc表示集散站点wi在调度方案s中所剩余的存储量，vc可用如下公式表示：

公式(3)中cb(s)表示物流仓库的仓储平衡度。cb(s)约束的目的在于保证各个集散站点仓库存储率的相对一致性。缺少此约束将导致算法为追求更低的运输成本，导致部分仓库仓库存储率过高，从而影响整体物流运送效率。

cb(s)＝d(cp(w(vc)))(8)

其中，vc表示集散站点wi在方案s中所余下的库存，cp表示库存占仓库容积的比例，d表示各集散站点的均方差。

公式(3)中lt(s)表示所装载货物需要送达的剩余时间。lt(s)约束的目的在于保证物流货物准时送达，当货物剩余配送时间不充足时，该货物将被率先配送，从而保证货物的准时送达。

其中，time表示在shi方案中物流车辆所装载货物剩余的配送时间，load表示在shi方案中物流车辆所装载的货物总量。

物流车辆调度算法的目标中，tr(s)，lu(s)，cc(s)三项目标的权重较高，它们直接影响着算法所追求的最低物流运输成本和最快物流运输速度。而cb(s)目标确保了各集散站点仓库储存率的相对平衡，lt(s)目标确保紧急货物的优先配送。同时，调度算法也必须满足以下约束：

其中，公式(10)确保在调度方案shi中物流车辆不能装载超出车辆总载重量的货物，公式(11)确保在调度方案shi中物流车辆从配送中心i运输至集散站点c的货物不会超过从在i点所有目的地为c点的所有货物的总和。

2、物流车辆智能调度算法。

(1)物流车辆智能调度算法总体框架。

各物流公司的站点仓库、货物信息、物流车辆数据库已趋于完善，本调度模型所使用的运算参数从物联网技术和物流公司信息数据库获得，包括物流车辆载重、位置信息，货物体积、剩余配送时间等，采用多目标优化算法，根据上文中所建立的调度模型和提出的优化目标进行求解，从而给出每辆物流车辆最佳的运输路线方案。物流车辆智能调度算法总体框架如图3所示。

算法中的g1指从配送中心w1发往各个集散站点wi的物流货物，同时因为集散站点不负责货物目的地整理，各个集散站点的货物需运输至配送中心进行整理。算法在前几步中优先接近超时货物的装载，第9步则是利用所建立的智能调度模型，根据库存情况、车辆状态、实时路况等综合因素，采用多目标优化算法以提高物流公司的运输能力并控制运输过程中的耗时。

(2)物流车辆智能调度算法编码。

设智能调度算法的解集为φ，解集中任意一个解pi，解的个数为k·n，其中k表示可投入运输工作的物流车辆总数，n表示物流仓库的总数。设解的元素为xij，当j＜n时，xij＝1表示物流车辆i负责目的地为j货物的运输，xij＝0表示物流车辆未装载到达该集散站点的货物。因为在现实运输过程中可能会出现车辆无负载进行运输工作的情况，因此通过xin表示是否安排空载前去配送中心。因此，算法的解空间为φ＝{pi}，种群空间为p＝{pi，i＝1，2，...cot}，其中，cot表示种群的总数。

对于任意一个解pi，当xij＝0，其中j≤n-1，并且xin＝1时，可得到如下公式：

shi(ld)＝0(12)

shi(pt)＝max_id(13)

其中，max_id表示仓储剩余量最大的集散站点编号。

否则，设可得到如下公式：

其中，shi(pt)表示在给定调度方案shi中，在给定的路网条件下，采用最短路径算法计算出成本最低的路线。这里采用遍历的思路，算法流程如图4所示

(3)物流车辆智能调度算法步骤。

智能调度算法基于遗传算法进行设计，其流程如图5所示。遗传的初始种群如上文所示，算法的优化方向由上文设计的tr(s)，lu(s)，cc(s)，lt(s)，cb(s)决定，采用交叉、变异、按目标择优选择的流程对调度方案换代优化。

以上所述仅为本发明的实施例，并非因此限制本发明的专利范围，凡是利用本发明说明书及附图内容所做的等效结构或等流程变换，或直接或间接运用在相关技术领域，均同理包括在本发明的专利保护范围。