基于分数阶热路模型的干式变压器温度计算方法及系统

本发明涉及干式变压器温度计算技术领域，尤其涉及一种基于分数阶热路模型的干式变压器温度计算方法及系统。

背景技术：

本部分的陈述仅仅是提供了与本发明相关的背景技术信息，不必然构成在先技术。

树脂绝缘干式变压器具有较好的绝缘性能和耐热性能，其但树脂材料的导热性能较差，达不到理想的散热效果，空载损耗和负载损耗会引起变压器温度升高，如果温升超出其绝缘材料的温升限制，可能会导致干式变压器发生故障，因此需要对干式变压器的温度场进行研究来掌握其内部温度状况。

发明人在研究中发现，干式变压器温度数据因为绝缘材料包裹的缘故不易直接测量，理论分析又大多比较复杂，由于变压器的发热和散热过程比较复杂，目前大部分研究是利用导热微分方程来建立变压器的温度场数学模型，再通过有限元法或者有限差分法进行求解。这种方法虽然可以对干式变压器的内部温度分布进行清晰的分析，但是其求解过程比较复杂，且对于不同的变压器需要建立不同的模型。

同时，现有技术大多是基于整数阶的，由于电容和热容在实际应用中都不是整数阶的，热路模型里的热容也应该是分数阶的形式，因此，往往会导致温度分布结果不准确。

技术实现要素：

为了解决上述问题，本发明提出了一种基于分数阶热路模型的干式变压器温度计算方法及系统，结合热电类比的理论以及热容的分数阶特性，提出干式变压器的含分数阶的热路模型及其分数阶方程组，通过预估-校正法推导离散后的分数阶热路模型方程，更符合热容特性，能够准确计算干式变压器的温度分布。

在一些实施方式中，采用如下技术方案：

一种基于分数阶热路模型的干式变压器温度计算方法，包括：

通过热电类比理论将热学参量类比为电学参量,利用热路等效原理和热容的分数阶特性，建立干式变压器的分数阶热路模型；

获取外界环境温度数据，铁心损耗、低压绕组损耗和高压绕组损耗数据，利用预估-校正法对干式变压器的分数阶热路模型进行求解，得到干式变压器铁芯、低压绕组、高压绕组的温度分布。

在另一些实施方式中，采用如下技术方案：

一种基于分数阶热路模型的干式变压器温度计算系统，包括：

分数阶热路模型建立模块，用于通过热电类比理论将热学参量类比为电学参量,利用热路等效原理和热容的分数阶特性，建立干式变压器的分数阶热路模型；

模型求解模块，用于获取铁心损耗、低压绕组损耗和高压绕组损耗数据，利用预估-校正法对干式变压器的分数阶热路模型进行求解，得到干式变压器铁芯、低压绕组、高压绕组的温度分布。

在另一些实施方式中，采用如下技术方案：

一种终端设备，其包括处理器和存储器，处理器用于实现各指令；存储器用于存储多条指令，所述指令适于由处理器加载并执行上述的基于分数阶热路模型的干式变压器温度计算方法。

在另一些实施方式中，采用如下技术方案：

一种计算机可读存储介质，其中存储有多条指令，所述指令适于由终端设备的处理器加载并执行上述的基于分数阶热路模型的干式变压器温度计算方法。

与现有技术相比，本发明的有益效果是：

本发明干式变压器的分数阶热路模型充分考虑了热容的分数阶特性，提高了干式变压器温度计算的准确性。

本发明方法只需获得环境温度，及干式变压器的铁芯及绕组损耗，按公式求得热容，热阻参数，就可以准确计算出干式变压器的温度分布；计算过程简单，计算结果准确。

本发明的其他特征和附加方面的优点将在下面的描述中部分给出，部分将从下面的描述中变得明显，或通过本方面的实践了解到。

附图说明

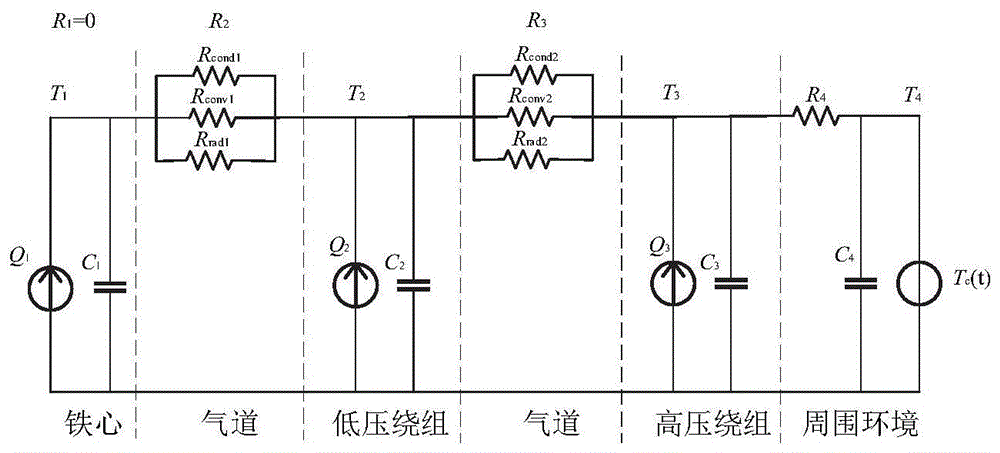
图1为本发明干式变压器的分数阶等效热路图；

图2为本发明实施例中分数阶方程组对温度的计算结果；

图3为本发明变压器内部散热示意图。

具体实施方式

应该指出，以下详细说明都是例示性的，旨在对本申请提供进一步的说明。除非另有指明，本发明使用的所有技术和科学术语具有与本申请所属技术领域的普通技术人员通常理解的相同含义。

需要注意的是，这里所使用的术语仅是为了描述具体实施方式，而非意图限制根据本申请的示例性实施方式。如在这里所使用的，除非上下文另外明确指出，否则单数形式也意图包括复数形式，此外，还应当理解的是，当在本说明书中使用术语“包含”和/或“包括”时，其指明存在特征、步骤、操作、器件、组件和/或它们的组合。

在不冲突的情况下，本发明中的实施例及实施例中的特征可以相互组合。

实施例一

根据本发明的实施例，公开了一种基于分数阶热路模型的干式变压器温度计算方法，根据热电类比思想，以及热容实际是分数阶的，提出干式变压的分数阶热路模型，并由整数阶热路方程过渡到分数阶方程组，利用预估-校正法求解干式变压器的温度分布。本方法模型搭建具有清晰的物理定义，数学模型充分考虑了分数阶特性，提高了干式变压器温度计算的准确性。

本实施例基于分数阶热路模型的干式变压器温度计算方法包括如下过程：

(1)通过热电类比理论将热学参量类比为电学参量,利用热路等效原理和热容的分数阶特性，建立干式变压器的分数阶热路模型；

(2)获取外界环境温度数据，铁心损耗、低压绕组损耗和高压绕组损耗数据，利用预估-校正法对干式变压器的分数阶热路模型进行求解，得到干式变压器铁芯、低压绕组、高压绕组的温度分布；其中，外界环境温度数据可以通过温度传感器获得。

基于得到的温度场分布，对于温度较高的区域，及时采取降温措施；比如：获取干式变压器铁芯、低压绕组或者高压绕组的温度分布后，如果某个位置超过设定的阈值时，则控制启动散热器工作，对干式变压器进行散热，避免因为温度过高导致的变压器故障。

具体地，热力学理论中的傅里叶定律和电路的欧姆定律表达式的结构相同，边界条件和几何形态相似，且在许多情况下，热量的传递和电荷的转移是相似的，可以将热学参量类比电学参量。

干式变压器的损耗为干式变压器温度场的热源，其散热方式一般有三种，即热传导、热对流和热辐射。干式变压器内部热量的传递是多种形式结合在一起的，如图3所示。

根据干式变压器的横向热传递情况，可通过热电类比理论将热学参量类比为电学参量。干式变压器在运行时会产生负载损耗和空载损耗等，这些损耗转变为热能，导致变压器各个部分存在温度差，从而产生了热传递过程，因此可将这些损耗看作理想热流源，类比为电路中的理想电流源。同时，外界环境的温度可看作理想温度源，类比为电路中的理想电压源，热传递过程中的比热容和热电阻可以类比为电路中的电容和电阻。具体的热电类比参数如表1所示。

表1热电类比参数

利用热传导，热对流，热辐射的传热理论得到模型中的各热阻参数；分析得到热等效电容参数；具体如下：

热传导遵循傅里叶定律，根据傅里叶定律，单位时间内通过物体截面的导热热量与当地的温度变化率及截面面积成正比，即：

式中，λ是比例系数，称为导热系数，ψ是导热热流量，a为垂直于热流方向的截面面积。由式(1)可得到热传导等效电阻rcond的计算公式为：

式中，λ为热导率，l为热传导的有效距离，s为热传导的有效面积。

对流换热是一个非线性过程，结合热对流公式，可得到对流热阻的计算公式为：

式中，h为固体表面传热系数，s为热对流的有效面积。

因热而发出辐射能的现象称为热辐射。热辐射所遵循的基本定律为斯特藩—玻耳兹曼定律，表达式为：

ψ＝aσt⁴(4)

式中，a为辐射表面积，t为热力学温度，σ为斯特藩—玻耳兹曼常量，其值为5.67×10^-5w/(m²·k⁴)，ψ为辐射通量密度。由此可得到辐射热阻的计算公式为：

式中，k为玻尔兹曼常数，k＝5.72×10^-8w/(m²·k⁴)，ε为辐射系数，s为热辐射的有效面积，t0和t1分别为辐射换热双方的温度。

热等效电容可以表示为质量与比热容的乘积，其计算公式为：

ci＝mici(6)

式中，mi表示变压器铁心或绕组的质量，ci表示硅钢片或铜的比热容。

在电路学理论中，实际的电容并不是传统意义上的整数阶元件，其在物理特性上均呈现分数阶特性，其分数阶数学模型为：

则根据热电类比理论，可以认为热路模型中的热容与电容相同，都具有分数阶特性，其分数阶数学模型为：

可以将变压器的铁心、高低压绕组、气道各个部分视为几个节点，并通过节点温度来反映变压器各部分的平均温度，各个节点之间通过不同的热交换方式下的热阻和热容来连接，其等效热路图如图1。

变压器铁心以及高低压绕组内部的传导热阻可以忽略不计，气道内的热阻可用对流热阻、传导热阻和辐射热阻并联来表示。图1中，q1为铁心损耗，q2、q3分别为低压绕组损耗和高压绕组损耗，rrad表示辐射热阻，rcond和rconv分别表示传导热阻和对流热阻，ci表示热容，ti表示各节点温度，tc(t)表示环境温度。

其中，r2、r3、r4为干式变压器的热阻参数，c1、c2、c3为干式变压器的热容参数。

以一台sc8—1000/10型干式变压器进行仿真。其中，铁心损耗q1＝2.07kw，低压绕组损耗q2＝4.227kw，高压绕组损耗q3＝3.033kw，环境温度取20℃，即293k。由该干式变压器的相关数据，根据式(2)～式(6)可求得相应热等效电路的模型参数，如表2所示。

表2干式变压器模型的参数值

利用干式变压器热路模型建立整数阶的热流守恒方程；根据图1可得到各个节点的热流守恒整数阶方程为：

由于电容和热容在实际应用中都不是整数阶的，热路模型里的热容也应该是分数阶的形式。因此，考虑热容的分数阶特性，将分数阶热容的数学模型与整数阶热流守恒方程结合，得到干式变压器的分数阶热路模型方程：

采用预估校正法对方程变形。在预估校正法，即广义的admas-bashforth-moulton方法中，对某一微分方程：

式中，[α]为大于α的最小整数。该微分方程可等价于volterra积分方程：

对式(12)的积分方程，可用复合梯形公式来计算其积分，取节点tj(j＝0,1,2,...,n+1)，令tn＝nh，n＝0,1,2,...,n(n∈z⁺)，h＝t/n，并对式(12)作离散化处理，即可得到：

上式中的aj,n+1为校正系数，校正系数计算公式为：

则式(12)的校正公式为：

若采用一步admas-bashforth规则代替一步admas-moulton规则，则预估项x^p(tn+1)可表示为：

其中预估校正系数可由下式求得：

因此，采用预估-校正法进一步推导离散后的分数阶热路模型方程,将t1、t2、t3替换为x、y、z：

根据离散后的分数阶热路模型方程，在matlab编程即可得到干式变压器铁芯、低压绕组、高压绕组的温度分布。计算结果如图2。

本发明含分数阶的干式变压器热路模型，准确求解了干式变压器的温度分布。本方法具有物理意义明晰的热路模型，考虑了热容的分数阶特性，只需测得铁芯及绕组上的损耗，用来等效热流源，就能得到较为理想的温度分布，可以适用于不同型号的干式变压器。

实验验证：

根据预估-校正法离散后的分数阶方程，在matlab中编制程序，即可进行分数阶微分方程组的求解。计算结果如图2。

将计算所得结果与实测数据进行比较，如表3所示。

表3计算结果与实测数据的比较

由表3可以看出，求解干式变压器热路模型的分数阶微分方程组所得结果与实测数据虽然存在一定的误差，但误差在允许范围内，说明该方法可以得到较为理想的干式变压器内部温度场分布。

实施例二

根据本发明的实施例，公开了一种基于分数阶热路模型的干式变压器温度计算系统，包括：

分数阶热路模型建立模块，用于通过热电类比理论将热学参量类比为电学参量,利用热路等效原理和热容的分数阶特性，建立干式变压器的分数阶热路模型；

模型求解模块，用于获取铁心损耗、低压绕组损耗和高压绕组损耗数据，利用预估-校正法对干式变压器的分数阶热路模型进行求解，得到干式变压器铁芯、低压绕组、高压绕组的温度分布。

需要说明的是，上述各模块的具体实现方式已经在实施例一中进行了详细的说明，不再赘述。

实施例三

根据本发明的实施例，公开了一种终端设备的实施例，其包括处理器和存储器，处理器用于实现各指令；存储器用于存储多条指令，所述指令适于由处理器加载并执行实施例一中所述的基于分数阶热路模型的干式变压器温度计算方法。

在另一些实施方式中，公开了一种计算机可读存储介质，其中存储有多条指令，所述指令适于由终端设备的处理器加载并执行实施例一中所述的基于分数阶热路模型的干式变压器温度计算方法。

上述虽然结合附图对本发明的具体实施方式进行了描述，但并非对本发明保护范围的限制，所属领域技术人员应该明白，在本发明的技术方案的基础上，本领域技术人员不需要付出创造性劳动即可做出的各种修改或变形仍在本发明的保护范围以内。