一种基于低秩张量自表示的深度子空间聚类方法及系统

本发明涉及一种基于低秩张量自表示的深度子空间聚类方法及系统。

背景技术：

子空间聚类是近年来广受关注和研究的聚类方法。子空间聚类通过将每组点拟合到它们所来自的子空间来分割数据，而基于谱的子空间聚类是近年来最流行的子空间聚类方法。在稀疏子空间聚类(sparsesubspaceclustering)和低秩表示(low-rankrepresentation)这两个方法的提出之后，自表示和谱聚类相结合的方法就开始流行。

稀疏子空间聚类的基本思想是假设高维空间中的同一类数据本质上属于同一个低维子空间，能够用同一个空间的其他数据点进行稀疏表示。它开创性地采用了l1正则化来限制用于重建每个样本的数据点数，取得较好的聚类性能。

低秩表示在自表示模型中对系数矩阵添加低秩约束，可以更好地获取数据的全局信息。由于噪声倾向于使系数矩阵的秩变高，因此低秩表示能够有效抑制噪声，提升鲁棒性。

这些传统的方法直接对原数据进行操作，特征表达能力不强。由于深度学习优异的特征提取能力，近年来有许多基于深度学习的深度子空间聚类方法相继提出。这类方法通过在深度自编码器中加入可学习的自表示层，有效地提升子空间聚类的性能。

但是，许多数据是以张量的形式存在，现有方法大部分都是将张量数据直接矢量化，从而导致空间结构信息丢失。

技术实现要素：

本发明目的在于提供一种基于低秩张量自表示的深度子空间聚类方法及系统，以解决上述现有技术存在的问题。

本发明所述一种基于低秩张量自表示的深度子空间聚类方法，其特征在于，包括以下步骤：

s1、数据的输入及预处理；

s2、在深度自编码器中引入张量与低秩矩阵的模积构建自表示层，用于对所述数据中的张量进行自表示；

s3、根据输入的数据对所述深度自编码器进行训练，得到所述深度自编码器的自表示系数矩阵c；

s4、利用所述自表示系数矩阵c构建对应的亲和矩阵；

s5、利用所述亲和矩阵进行谱聚类操作，得到聚类结果。

用于学习的损失函数为：

其中，χ是预处理后的张量，是张量χ经过自表示层和反卷积层后得到的重构矩阵，λ和γ是超参数，ζ是经过深度自编码器后得到的特征张量，×i是张量ζ第i个维度与对应矩阵的模积运算，u1和v1是特征张量ζ样本维度自表示系数矩阵的低秩分解，自表示系数矩阵c＝u1v1，自表示后重构张量的作为反卷积层的输入。

所述步骤s4中利用指定个数最大值的硬阈值策略和基于幂乘运算的软阈值策略相结合，构建亲和矩阵。

所述步骤s4具体为：

对自表示系数矩阵c的每一列进行最大范数归一化得到矩阵

令矩阵

对矩阵g1的每一列保留指定个数的最大值，其余位置置零；

对矩阵g1的每一列进行最大范数归一化得到矩阵

令矩阵

最后得到亲和矩阵

一种基于低秩张量自表示的深度子空间聚类系统，包括输入模块、计算模块和输出模块；所述输入模块用于输入数据至所述计算模块；所述输出模块用于输出所述计算模块的计算结果；所述计算模块用于对输入的数据以所述深度子空间聚类方法进行计算。

本发明所述基于低秩张量自表示的深度子空间聚类方法及系统，其优点在于，将张量与矩阵的模积运算替换掉传统的直接矢量化方法，保留了数据本身的空间维度，计算损失时带来更好的效果。相比现有的深度子空间聚类算法，本发明的自表示系数矩阵分解为u×v的维度，所需网络参数少，并且加入约束低秩的正则化项，聚类效果得到提升。将选取指定个最大值的硬阈值策略和基于幂乘运算的软阈值策略相结合，给定了一种新的亲和矩阵构造方法。本发明构造的亲和矩阵对样本联结性的描述更加准确。

附图说明

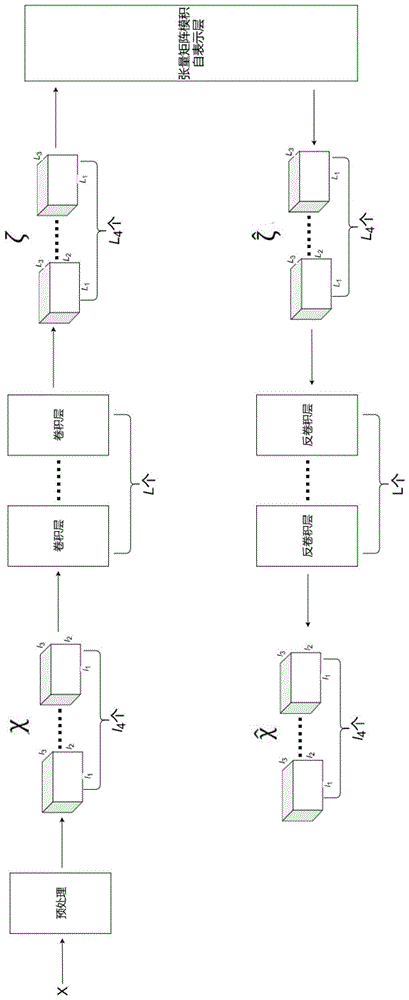
图1是本发明所述深度子空间聚类网络结构示意图；

图2是本发明所述自表示层的网络结构示意图。

具体实施方式

张量是一个多维的数据存储形式，数据的维度被称为张量的阶，可以看成是向量和矩阵在多维空间中的推广。张量与矩阵的模积(mode-nproduct)是张量的运算之一，其主要思想是将张量的一个维度重新整合成矩阵和另一个矩阵相乘，是矩阵乘法在张量空间的推广。利用张量与矩阵的模积运算可以使得高阶张量数据每一个维度都参与运算并保持原有的空间信息。本发明还将张量与矩阵的模积作为自表示的方法，融入到深度自编码器中，保留了张量空间结构信息，得到更好的聚类效果。

本发明所述基于低秩张量自表示的深度子空间聚类方法首先对数据进行预处理，得到预处理的数据。然后在深度自编码器中，引入张量与低秩矩阵的模积用于张量数据的自表示，根据输入数据对深度自编码器进行训练。最后根据深度自编码器的张量自表示系数矩阵，构建亲和矩阵，将亲和矩阵进行谱聚类得到聚类结果。

下面通过具体数据参数和实现过程对发明作进一步详细的描述，具体如图1、2所示。

为方便后续描述，对涉及到的符号进行约定。对于卷积层的权重描述为ω∈r^c×k×d×d，其中，c为输入通道数，k为输出通道数(即卷积核个数)，d×d为卷积核大小。

深度学习低秩张量子空间聚类方法，包括：

s1、对数据x进行预处理，即重新编排数据，令编排后其中l1表示图片的个数，l2表示通道数，l3×l4为图片的尺寸大小。

s2、构建一个网络，包括l个卷积层，参数为其中ωi表示第i个卷积层的权重，后跟一个用张量和矩阵模积运算构建的自表示层，然后l个反卷积层，参数为其中ωk表示第k个反卷积层的权重，经过反卷积层后输出重构的数据。

下面具体地讲述张量和矩阵模积运算：

令，张量矩阵则张量和矩阵模积定义为

如以下具体实例：χ∈r^3×4×2，

矩阵z∈r^2×4，则(χ×1z)＝γ∈r^2×4×2，

其中，

s3、设计损失函数，对网络进行训练。

输入数据经过预处理后变成张量经过l个卷积层后输出张量对张量ζ在每个维度利用张量模积进行自表示，每个维度的系数矩阵表示为矩阵ui和vi的乘积，其中将自表示重构后的张量作为反卷积层的输入。经过自表示层和反卷积层后，得到重构张量

令损失函数具体为：

其中λ和γ是超参数，即各项的系数。

s4、网络训练好后，得到了自表示的样本维度的u1和v1。

下面构建亲和矩阵，具体步骤如下：

由c＝u1v1得到自表示系数矩阵，然后对c每一列进行最大范数归一化得到

计算

每一列保留g1的最大k个数，其余置零；

然后对g1每一列进行最大范数归一化得到

计算

构造亲和矩阵其中矩阵g1为亲和矩阵g在计算过程中的过渡矩阵。

s5、将各矩阵应用至谱聚类算法，得到聚类标签。还可选择性计算聚类准确率。

本发明同时还提供一种基于低秩张量自表示的深度子空间聚类系统，包括输入模块、计算模块和输出模块；所述输入模块用于输入数据至所述计算模块；所述输出模块用于输出所述计算模块的计算结果；所述计算模块用于对输入的数据以所述深度子空间聚类方法进行计算。

对于本领域的技术人员来说，可根据以上描述的技术方案以及构思，做出其它各种相应的改变以及形变，而所有的这些改变以及形变都应该属于本发明权利要求的保护范围之内。