一种球柱联合转台轴承疲劳寿命计算方法

本发明属于轴承技术领域，具体涉及一种球柱联合转台轴承疲劳寿命计算方法。

背景技术：

球柱联合转台轴承综合性能优异，可以同时承受径向载荷、轴向载荷和倾覆力矩，并且具有长疲劳寿命、低摩擦力矩和高刚度等优点，因此其可用在数控机床转台、天文望远镜转台等对轴承性能要求较高的场合。疲劳失效是轴承的主要失效形式之一，球柱联合转台轴承的疲劳寿命直接影响了数控机床和天文望远镜等主机的寿命和可靠性，是在球柱联合转台轴承设计及使用环节中必须要考虑的重要因素。因此，球柱联合转台轴承疲劳寿命的准确计算是进行轴承性能分析及优化设计的基础，对提升主机可靠性具有重要意义。

技术实现要素：

本发明的目的是提供一种球柱联合转台轴承疲劳寿命计算方法，以解决对球柱联合转台轴承疲劳寿命分析计算的需求。

为了达到上述目的，本发明所采用的技术方案是：一种球柱联合转台轴承疲劳寿命计算方法，包括以下步骤：

步骤一：根据球柱联合转台轴承结构形式及受力特点建立轴承的受载分析模型；

步骤二：根据球柱联合转台轴承的力学平衡特点建立轴承的力学平衡方程，代入相关参数对平衡方程求解，得出轴承的载荷分布；

步骤三：将球柱联合转台轴承看作由不同类型轴承组成的组合轴承，将其分解为若干套不同类型的轴承；

步骤四：基于球柱联合转台轴承的载荷分布，分别计算各套轴承的疲劳寿命；

步骤五：根据各套轴承的疲劳寿命计算结果，确定对球柱联合转台轴承疲劳寿命影响较大的轴承类型；

步骤六：确定计算球柱联合转台轴承疲劳寿命的公式形式；

步骤七：基于计算公式对球柱联合转台轴承疲劳寿命进行计算分析。

进一步的，所述的步骤三，在对球柱联合转台轴承进行分解时，将其分解为四套推力球轴承和一套圆柱滚子轴承。

进一步的，所述的步骤五，在确定对球柱联合转台轴承疲劳寿命影响较大的轴承类型时，取计算寿命平均值最低的一套轴承为对球柱联合转台轴承疲劳寿命影响较大的轴承类型。

与现有技术相比，本发明的有益效果是：本发明将球柱联合转台轴承看作由不同类型轴承组成的组合轴承，将其分解为若干套不同类型的轴承，然后，基于球柱联合转台轴承的载荷分布，分别计算各套轴承的疲劳寿命，最后在确定对球柱联合转台轴承疲劳寿命影响较大的轴承类型时，取计算寿命平均值最低的一套轴承为对球柱联合转台轴承疲劳寿命影响较大的轴承类型，从而能够更精准的计算球柱联合转台轴承的疲劳寿命，对提升主机可靠性具有重要意义。

附图说明

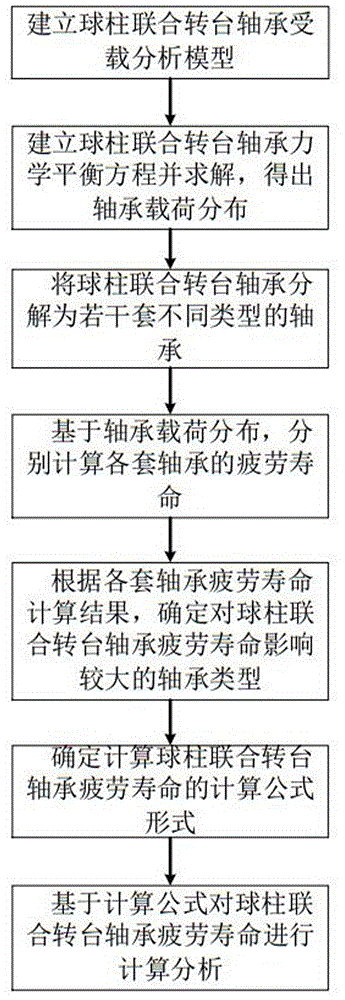
图1是本发明一种球柱联合转台轴承疲劳寿命计算方法的流程示意图；

图2是本发明实施例中涉及的某型号球柱联合转台轴承的结构示意图；

图3是球柱联合转台轴承受载变形示意图；

图中标记：1、轴向第三排钢球，2、轴向第四排钢球，3、外圈，4、保持架，5、径向排滚子，6、轴向第一排钢球，7、轴向第二排钢球，8、内圈，9、连接螺钉。

具体实施方式

为使本发明实施例的目的、技术方案和优点更加清楚，下面将结合本发明中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例是本发明一部分实施例，而不是全部的实施例，基于本发明中的实施例，本领域普通技术人员在没有作出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。

一种球柱联合转台轴承疲劳寿命计算方法，如图1所示，包括以下步骤，

步骤一：根据转台轴承结构形式及受力特点建立轴承的受载分析模型。

以下以图2所示的某型号球柱联合转台轴承对本发明的方案进行说明，如图2所示，该球柱联合转台轴承的轴向上排滚动体、轴向下排滚动体均由两列交错排布的钢球组成，径向排滚动体由一列圆柱滚子组成。

由球柱联合转台轴承的具体使用工况可知，其在运转过程中承受的载荷有轴向载荷fa、径向载荷fr和倾覆力矩m0。这些载荷最终会传递到球柱联合转台轴承滚动体上引起滚动体的受载变形，其示意图如图3所示。其中，δa为内圈在受载后产生的轴向位移，δr为内圈产生的径向位移，θ为内圈在承受负载后转动的角度，dm1为第一列钢球的节圆直径，dm2为第二列钢球的节圆直径，dm3为径向排滚子的节圆直径。表示第一列钢球的位置角，表示第二列钢球的位置角。

由图3所示的几何关系推导可得，在轴向载荷、径向载荷和倾覆力矩的共同作用下，上排第1列第i个钢球中心处的法向变形量为：

上排第2列第i个钢球中心处的法向变形量为：

式中，为第k列第i个钢球的位置角，在最大变形处z为每列的钢球个数；ua0为初始轴向游隙。

下排第1列第i个钢球中心处的法向变形量为：

下排第2列第i个钢球中心处的法向变形量为：

由赫兹点接触理论，每个钢球所承受的载荷大小为：

式中，k1为刚度系数：

式中，kin为滚动体与外圈的负荷-变形常数，ko为滚动体与内圈的负荷-变形常数。

则轴承上排第1列第i个钢球受到的法向载荷为：

轴承上排第2列第i个钢球受到的法向载荷为：

轴承下排第1列第i个钢球受到的法向载荷为：

轴承下排第2列第i个钢球受到的法向载荷为：

滚子轴承在设计过程中，通常要对滚子进行修型处理，如对数修型、圆弧修型等，以改善滚子的应力分布状态，提升轴承的疲劳寿命等性能。球柱联合转台轴承的径向排滚子长度较长，采用修型处理可导致沿滚子母线方向上的载荷分布出现差异，因此不宜将滚子视为一个整体进行分析。本文采用“切片法”将每一个滚子沿母线方向均分为n片，每个切片的厚度为w＝l/n，分别计算每片滚子所承受的载荷，最终将各片滚子的载荷累加得到滚子整体的载荷，切片个数n值越大载荷分布计算越精确。径向排第i个滚子第j个切片中心处两滚道面间的法向趋近量为：

式中，为径向排滚子的位置角，ur0为径向初始游隙。

由赫兹线接触理论可得，每个切片所承受的载荷大小为：

则累加可得径向排第i个滚子的载荷为：

步骤二：根据轴承的力学平衡特点建立轴承的力学平衡方程，代入相关参数对平衡方程求解，得出轴承的载荷分布。

为求解滚动体的载荷分布，需要建立球柱联合转台轴承的力学平衡方程。由工况可知球柱联合转台轴承内圈在外力(轴向力fa、径向力fr、倾覆力矩m)和内力(滚动体与滚道的接触力)共同作用下处于平衡状态，则可建立如下方程：

轴向方向上的力学平衡方程为：

径向方向上的力学平衡方程为：

力矩平衡方程为：

基于上述方程，编写相关计算程序，代入轴承结构参数和工况参数，进行迭代求解，得出轴承的载荷分布。

步骤三：将球柱联合转台轴承看作由不同类型轴承组成的组合轴承，将其分解为若干套不同类型的轴承。

球柱联合转台轴承可看作一种组合轴承，其由四套推力球轴承和一套圆柱滚子轴承组成。在计算其寿命时，则根据组合轴承寿命计算方法，先计算每套轴承的疲劳寿命，再代入组合轴承的疲劳寿命计算公式，即可得到轴承的整体寿命。

步骤四：基于轴承的载荷分布，分别计算各套轴承的疲劳寿命。

推力球轴承一的基本额定动载荷为：

式中f为套圈沟曲率半径系数，ε为球轴承寿命计算修正系数。

由于轴承外圈固定，内圈旋转，则相对于负荷方向旋转的套圈为内圈，推力球轴承一内圈当量滚动体载荷为：

则推力球轴承一内圈的额定寿命为：

推力球轴承一外圈当量滚动体载荷为：

则推力球轴承一外圈的额定寿命为：

则推力球轴承一的寿命为：

推力球轴承二的基本额定动载荷为：

推力球轴承二内圈当量滚动体载荷为：

则推力球轴承二内圈的额定寿命为：

推力球轴承二外圈当量滚动体载荷为：

则推力球轴承二外圈的额定寿命为：

则推力球轴承二的寿命为：

推力球轴承三的基本额定动载荷为：

推力球轴承三内圈当量滚动体载荷为：

则推力球轴承三内圈的额定寿命为：

推力球轴承三外圈当量滚动体载荷为：

则推力球轴承三外圈的额定寿命为：

则推力球轴承三的寿命为：

推力球轴承四的基本额定动载荷为：

推力球轴承四内圈当量滚动体载荷为：

则推力球轴承四内圈的额定寿命为：

推力球轴承四外圈当量滚动体载荷为：

则推力球轴承四外圈的额定寿命为：

则推力球轴承四的寿命为：

圆柱滚子轴承内圈的基本额定动载荷为：

式中的λi和公式45中的λo为考虑到滚子边缘受载以及偏心载荷所引起的应力集中现象的修正系数，λi＝λo＝0.61；l为滚子长度；z1为径向排滚子个数，dw为径向排滚子直径。

γ为无量纲几何参数，其表达式为：

式中α为径向排滚子接触角。

内圈的当量滚动体载荷为：

内圈的额定疲劳寿命为：

外圈的基本额定动载荷为：

外圈上的当量滚动体载荷为：

外圈的额定疲劳寿命为：

则径向排滚子轴承的额定寿命为：

步骤五：根据各套轴承疲劳寿命计算结果，确定对球柱联合转台轴承疲劳寿命影响较大的轴承类型。

代入轴承的相应工况参数，计算出各套轴承疲劳的寿命，可得轴向排推力球的计算寿命平均值低于径向排滚子轴承的疲劳寿命平均值，则对球柱联合转台轴承疲劳寿命影响较大的是轴向排推力球轴承。公式(49)为球柱联合转台轴承疲劳寿命计算公式的一般形式，式中β为公式的指数。

步骤六：确定计算球柱联合转台轴承疲劳寿命的公式形式。

基于步骤五的分析结果，公式(49)中的指数β取值为轴向排推力球指数的倒数球柱联合转台轴承的寿命计算公式为：

步骤七：基于计算公式对球柱联合转台轴承疲劳寿命进行计算分析。

将各套轴承的疲劳寿命代入公式(50)，即可求出球柱联合转台轴承的疲劳寿命。

对所公开的实施例的上述说明，使本领域专业技术人员能够实现或使用本发明。对这些实施例的多种修改对本领域的专业技术人员来说将是显而易见的，本文中所定义的一般原理可以在不脱离本发明的精神或范围的情况下，在其它实施例中实现。因此，本发明将不会被限制于本文所示的这些实施例，而是要符合与本文所公开的原理和新颖特点相一致的最宽的范围。