基于离散填充函数的无环图划分方法及系统

本发明涉及超大规模集成电路(vlsi)物理设计自动化技术领域，具体涉及一种基于离散填充函数的无环图划分方法及系统。

背景技术：

在电路设计中，从布局到逻辑仿真和仿真都可以运用划分的方法。例如，划分是降低物理设计复杂性的一种常用方法，它将一个大型的vlsi电路划分为可以单独有效设计的较小的子电路。划分问题是将一个电路划分成若干子电路，使每个子电路的大小满足平衡约束，即其大小在规定的范围内，且子电路之间的连接数(割边)数量最小。

为了减少仿真运行时间，多数采用并行仿真的方法。它将一个大型电路分割成多个子电路。由于超大规模集成电路的规模不断增大，所需的仿真精度越来越高,我们希望将一个大的电路划分成块，这样块就可以在每个处理器进行并行模拟。在划分的过程中，致力于最小化块之间的互连数量，以增强块的独立性，为并行处理提供更优的解。特别地，不同块之间的循环相依性导致不必要的重新运行，导致并行模拟框架的性能变低。为了获得更高的仿真吞吐量，在并行仿真中考虑信号方向是至关重要的。

技术实现要素：

有鉴于此，本发明的目的在于提供一种基于离散填充函数的无环图划分方法，有效提高电路划分质量和效率。

一种基于离散填充函数的无环图划分方法，包括以下步骤：

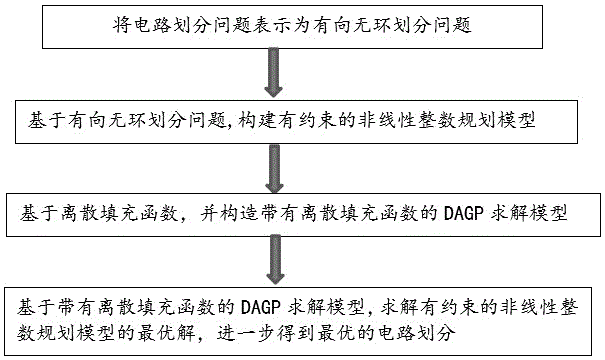
步骤s1：将电路划分问题表示为有向无环划分问题；

步骤s2:基于有向无环划分问题,构建有约束的非线性整数规划模型；

步骤s3:基于离散填充函数，并构造带有离散填充函数的dagp求解模型；

步骤s4:基于带有离散填充函数的dagp求解模型，求解有约束的非线性整数规划模型的最优解，进一步得到最优的电路划分。

进一步的，所述步骤s1具体为：将电路转换为有向图，每个顶点代表一个逻辑门，如果逻辑门的输出为另一个逻辑门的输入，就在这两个顶点之间连接一条输入指向输出的有向边。

进一步的，所述步骤s2具体为:将有向无环划分问题表述为一个有约束的非线性整数规划问题，其数学公式如下：

其中(vi，vj)表示顶点vi与vj所连接的边，y厸j为二进制变量，表达式为：

逻辑电路中割边的总权重通过来计算，x为满足平衡约束和无环约束的解集，k表示划分后块的数量；

离散填充辅助函数公式：

其中为有向无环划分问题的当前最佳离散局部最小值，κ为非负参数，然后将有向无环划分问题转化为辅助有向无环图划分问题，构建有约束的非线性整数规划模型，表达式如下：

辅助有向无环图划分问题的目标是寻找有向无环划分问题的离散局部最小值，即比当前最佳的还小的值。

进一步的，所述步骤s3具体为：寻找最小化a(x，κ)的离散局部最优解x′,具体有三种情况：

(1)：这种情况下即为找到比更好的解，需要更新辅助函数a(x，κ)；

(2)：这种情况下算法收敛到从新的初始解再次寻找最优解；

(3)：以及这种情况下，当前解没有优于增加参数κ的值。

一种基于离散填充函数的无环图划分系统，包括处理器、存储器以及存储在所述存储器上的计算机程序，所述处理器执行所述计算机程序时，具体执行如上所述的无环图划分方法中的步骤。

为实现上述目的，本发明采用如下技术方案：

本发明与现有技术相比具有以下有益效果：

本发明考虑具有平衡和非圈约束的图划分，有效提高电路划分质量和效率。

附图说明

图1是本发明一实施例中的方法流程图。

具体实施方式

下面结合附图及实施例对本发明做进一步说明。

请参照图1，本发明提供一种基于离散填充函数的无环图划分方法，包括以下步骤：

步骤s1：将电路划分问题表示为有向无环划分问题；

步骤s2:基于有向无环划分问题,构建有约束的非线性整数规划模型；

步骤s3:基于离散填充函数，并构造带有离散填充函数的dagp求解模型；

步骤s4:基于带有离散填充函数的dagp求解模型，求解有约束的非线性整数规划模型的最优解，进一步得到最优的电路划分。

优选的，在本实施例中，所述步骤s1具体为：将电路转换为有向图，每个顶点代表一个逻辑门，如果逻辑门的输出为另一个逻辑门的输入，就在这两个顶点之间连接一条输入指向输出的有向边。

优选的，在本实施例中，所述步骤s2具体为:将有向无环划分问题表述为一个有约束的非线性整数规划问题，其数学公式如下：

其中(vi，vj)表示顶点vi与vj所连接的边，y厸j为二进制变量，表达式为：

逻辑电路中割边的总权重通过来计算，x为满足平衡约束和无环约束的解集，k表示划分后块的数量；

离散填充辅助函数公式：

其中为有向无环划分问题的当前最佳离散局部最小值，κ为非负参数，然后将有向无环划分问题转化为辅助有向无环图划分问题，构建有约束的非线性整数规划模型，表达式如下：

辅助有向无环图划分问题的目标是寻找有向无环划分问题的离散局部最小值，即比当前最佳的还小的值。

在本实施例中，所述步骤s3具体为：寻找最小化a(x，κ)的离散局部最优解x′,具体有三种情况：

(1)：这种情况下即为找到比更好的解，需要更新辅助函数a(x，κ)；

(2)：这种情况下算法收敛到从新的初始解再次寻找最优解；

(3)：以及这种情况下，当前解没有优于增加参数κ的值。

本领域内的技术人员应明白，本申请的实施例可提供为方法、系统、或计算机程序产品。因此，本申请可采用完全硬件实施例、完全软件实施例、或结合软件和硬件方面的实施例的形式。而且，本申请可采用在一个或多个其中包含有计算机可用程序代码的计算机可用存储介质(包括但不限于磁盘存储器、cd-rom、光学存储器等)上实施的计算机程序产品的形式。

本申请是参照根据本申请实施例的方法、设备(系统)、和计算机程序产品的流程图和/或方框图来描述的。应理解可由计算机程序指令实现流程图和/或方框图中的每一流程和/或方框、以及流程图和/或方框图中的流程和/或方框的结合。可提供这些计算机程序指令到通用计算机、专用计算机、嵌入式处理机或其他可编程数据处理设备的处理器以产生一个机器，使得通过计算机或其他可编程数据处理设备的处理器执行的指令产生用于实现在流程图一个流程或多个流程和/或方框图一个方框或多个方框中指定的功能的装置。

这些计算机程序指令也可存储在能引导计算机或其他可编程数据处理设备以特定方式工作的计算机可读存储器中，使得存储在该计算机可读存储器中的指令产生包括指令装置的制造品，该指令装置实现在流程图一个流程或多个流程和/或方框图一个方框或多个方框中指定的功能。

这些计算机程序指令也可装载到计算机或其他可编程数据处理设备上，使得在计算机或其他可编程设备上执行一系列操作步骤以产生计算机实现的处理，从而在计算机或其他可编程设备上执行的指令提供用于实现在流程图一个流程或多个流程和/或方框图一个方框或多个方框中指定的功能的步骤。

以上所述，仅是本发明的较佳实施例而已，并非是对本发明作其它形式的限制，任何熟悉本专业的技术人员可能利用上述揭示的技术内容加以变更或改型为等同变化的等效实施例。但是凡是未脱离本发明技术方案内容,依据本发明的技术实质对以上实施例所作的任何简单修改、等同变化与改型，仍属于本发明技术方案的保护范围。