一种基于神经网络回归的单粒子瞬态效应建模方法

本发明涉及一种单粒子瞬态效应建模方法，具体涉及一种基于神经网络回归的单粒子瞬态效应建模方法。

背景技术：

随着晶体管尺寸和电源电压的不断缩小，对单粒子瞬态效应(set)的敏感性已成为航天集成电路在辐射环境下最重要的可靠性问题之一。通常，可以通过计算机辅助建模和仿真，对集成电路的单粒子效应的灵敏性进行评估和分析，也可以通过实验的方法对集成电路的单粒子效应的灵敏性进行测试。由于辐照实验机时紧张，费用高昂，电路级单粒子瞬态效应仿真适用于在设计阶段分析了解电路对单粒子瞬态效应的响应，以及如何分析、如何加固电路，避免电路中产生单粒子瞬态效应。

然而，单粒子瞬态效应模型的准确性直接影响到电路级单粒子效应仿真的准确性，为了获得准确的单粒子瞬态效应模型，许多研究者提出了各种方法来建立set模型。目前的建模方法主要分为两类，一类是基于物理机理的单粒子瞬态建模，一类是基于特定函数(如：双指数函数、威布尔函数等)拟合的单粒子瞬态模型。前者通过研究单粒子效应在器件中的物理机制，构建出的单粒子瞬态模型精度较高，但模型复杂度高，不适用于电路级单粒子效应仿真分析。后者模型简单，但基于特定函数的拟合模型，很难保证模型的精度，特别是考虑各种单粒子效应变量，如现行能量转移(let)，粒子轰击位置和偏置电压等变量。

技术实现要素：

本发明的目的是解决现有基于物理机理的单粒子瞬态建模存在模型复杂度高、不适用电路级单粒子效应仿真分析，而基于特定函数拟合的单粒子瞬态建模很难保证模型的精度的技术问题，提出一种基于神经网络回归的单粒子瞬态效应建模方法，可为电路级单粒子效应仿真提供准确的单粒子瞬态效应模型。

为了实现上述目的，本发明所采用的技术方案是：一种基于神经网络回归的单粒子瞬态效应建模方法，其特征在于，包括以下步骤：

步骤1、针对目标工艺，建立场效应管器件结构模型；

步骤2、采用tcad对器件结构模型进行仿真，获得不同因素条件下单粒子效应产生的漏极瞬态电流脉冲曲线；

步骤3、根据精度需求，对漏极瞬态电流脉冲曲线进行抽样，获得不同时间、不同let条件下的离散数据；

步骤4、将步骤3得到的离散数据随机分成训练集、验证集和测试集；

步骤5、构建基于神经网络的单粒子瞬态效应模型，通过学习拟合，用训练集和验证集对单粒子瞬态效应模型进行训练和验证，然后用测试集对训练后的单粒子瞬态效应模型进行漏极电流精度测试，获得测试曲线；

步骤6、将测试曲线与步骤2中仿真得到的漏极瞬态电流脉冲曲线进行对比，判断误差是否低于设定阈值：

若否，则调整神经网络的单粒子瞬态效应模型参数，返回步骤5；

若是，则训练完成，获得单粒子瞬态效应模型。

进一步地，步骤5中，所述神经网络为多层前馈神经网络；所述学习拟合采用levenberg–marquardt算法；

所述多层前馈神经网络包括输入层、输出层及至少一层隐藏层；所述输入层神经元个数与单粒子瞬态效应模型输入变量一致，所述隐藏层包括至少1个神经元；所述输出层包括1个神经元；本发明可以通过调整隐藏层的个数和每个隐藏层包含的神经元个数，提高模型拟合精度。

进一步地，所述输入层包括3个神经元；所述隐藏层为两层，每层隐藏层包括8个神经元；所述输入层与隐藏层之间引入归一化操作，所述输出层之后引入去归一化操作，归一化操作简化了多层前馈神经网络的计算方法，提高建模效率。

进一步地，所述隐藏层采用tansig函数作为传输函数，所述输出层采用pureline函数作为传递函数，具体公式如下：

fpureline(x)＝x

其中：ftansig(x)为tansig函数；fpureline(x)为pureline函数，x为变量。

进一步地，步骤3中，所述对漏极瞬态电流脉冲曲线进行抽样，具体为：

对漏极瞬态电流源曲线抽样采用分段均匀取样，在漏极瞬态电流源前半段电流变化较快的区间采用高频率采样，在漏极瞬态电流源后半段电流变化平缓的区间采用低频率采样，既保证了取样精度，又减少了计算量。

进一步地，步骤6中，所述设定阈值为均方误差0.0001。

进一步地，步骤1中，所述器件结构模型参数包括栅长、栅宽、栅氧厚度、源/漏掺杂浓度及沟道掺杂浓度中的任意多种。

进一步地，步骤2中，所述因素条件包括let、温度、入射位置、入射角度及漏极偏置中的任意多种。

进一步地，所述let取值范围为0.1～100mev.cm²/mg；所述漏极偏置电压范围为0～1.5vdd。

进一步地，步骤4中，所述训练集、验证集及测试集的设置比例为：训练集65％～75％，验证集10％～20％，测试集10％～20％。

本发明的有益效果是：

1)本发明基于神经网络回归的单粒子瞬态效应建模方法，采用tcad对器件结构模型进行仿真，获得不同因素条件下单粒子效应产生的漏极瞬态电流脉冲曲线，通过神经网络进行学习拟合，最终获得单粒子瞬态效应模型，本发明可为电路级单粒子效应仿真提供准确的单粒子瞬态效应模型。

2)本发明对漏极瞬态电流源曲线抽样采用分段均匀取样，在漏极瞬态电流源前半段电流变化较快的区间采用高频率采样，在漏极瞬态电流源后半段电流变化平缓的区间采用低频率采样，在保证取样精度的同时，减少了计算量。

3)本发明采用多层前馈神经网络进行学习拟合，引入了多个隐藏层，通过调整隐藏层的层数和每层包含的神经元个数，可以提高模型拟合精度，最终提高了单粒子瞬态效应模型的精度。

4)本发明采用的多层前馈神经网络输入层由时间、线性能量转移(let)、漏极偏置电压构成，输入变量的单位不同，因此在输入层与隐藏层之间引入归一化操作，在输出层之后引入去归一化操作，简化了多层前馈神经网络的计算方法，提高了建模效率。

附图说明

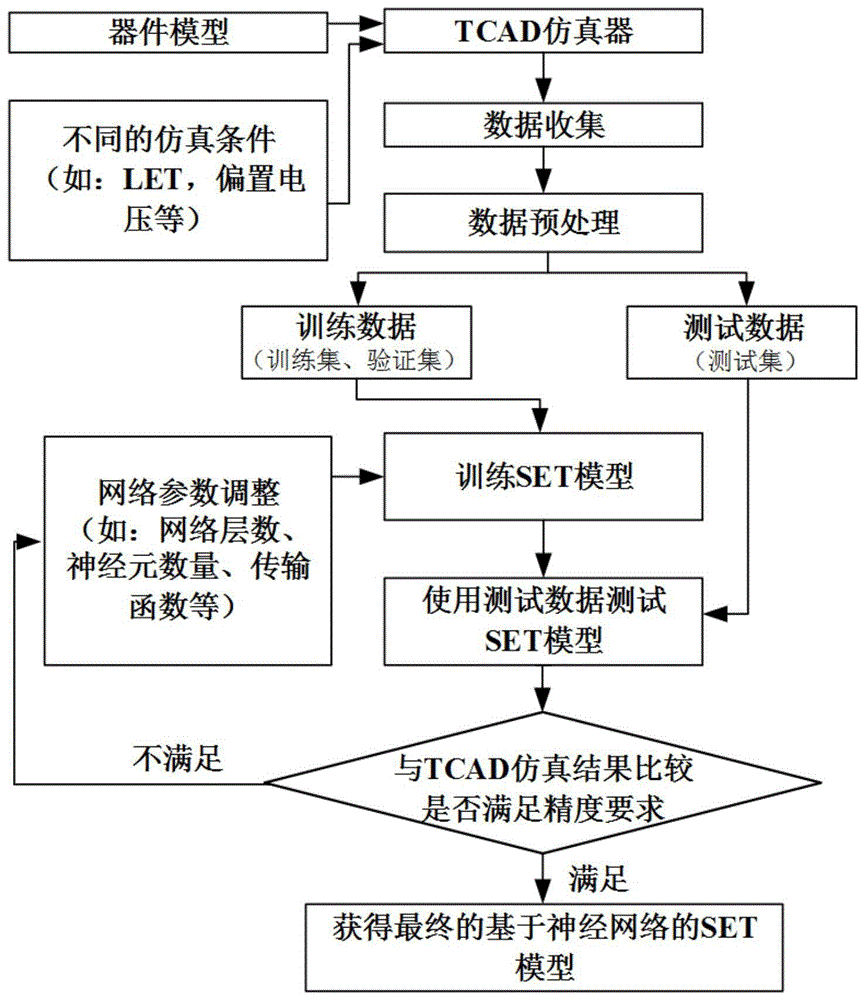
图1为本发明基于神经网络回归的单粒子瞬态效应建模方法流程图；

图2为本发明实施例中针对目标工艺建立的器件结构模型示意图；

图3为本发明实施例中漏极瞬态电流源曲线抽样采用分段均匀取样示意图；

图4为本发明实施例中多层前馈神经网络示意图；

图5为本发明实施例中基于神经网络回归的set模型测试与tcad仿真结果对比图。

具体实施方式

为了更清楚地说明本发明的技术方案，下面结合附图和具体实施例对本发明进行详细说明。

本发明提出一种基于神经网络回归的单粒子瞬态效应建模方法，可为电路级单粒子效应仿真提供准确的单粒子瞬态效应模型。

通常用线性能量转移(linearenergytransfer，let)表征单粒子效应作用的强弱，let表示单位路径上损失的能量，将let除以材料密度归一化处理后，单位为mev·cm²/mg，如下式所示：

仿真工具tcad(technologycomputeraideddesign)为半导体工艺模拟以及器件模拟工具，可用于分析let、温度、入射位置、入射角度、漏极偏置这些因素对nmos器件单粒子电流脉冲的影响。

如图1所示，为基于神经网络回归的单粒子瞬态效应建模方法流程图，具体建模步骤如下：

1)针对目标工艺(如中芯国际130nm工艺)，建立场效应管结构模型(包含：几何尺寸、工艺参数等)，本发明实施例以中芯国际130nm工艺nmos器件为例，栅长为130nm，栅宽为420nm，栅氧厚度为2.58nm，源/漏掺杂浓度为10²⁰cm^-3，沟道掺杂为1.57×10¹⁷cm^-3，所构建的器件模型如图2所示。

2)采用tcad仿真工具，分析let、温度、入射位置、入射角度、漏极偏置等因素对nmos器件单粒子电流脉冲的影响，通过仿真获得不同因素下单粒子效应产生的漏极瞬态电流脉冲曲线。一般let取值范围为0.1～100mev.cm²/mg，可以覆盖元素周期表的1～92号元素在器件内的let作用范围，漏极偏置电压范围为0～1.5vdd。

本发明实施例中，let取值范围为0.1～100mev.cm²/mg，漏极偏置电压范围为0～1.8v(vdd为1.2v)，粒子入射深度选取10μm，随机选取不同的let和漏极偏置电压组合作为仿真设置条件，通过多次仿真获得大量不同let和漏极偏置电压组合条件下的漏极偏置电压数据。

3)根据精度需要，漏极瞬态电流脉冲曲线进行抽样，获得不同时间、不同let等条件下的离散数据。

对漏极瞬态电流源曲线抽样采用分段均匀取样，在漏极瞬态电流源前半段电流变化较快的区间采用高频率采样，在漏极瞬态电流源后半段采用低频率采样。在本发明的优选实施例中，如图3所示，0～300ps区间，抽样频率为4e12hz，300～1000ps区间，抽样频率为1.4e11hz，最终获得418000组数据。

4)将数据随机分成训练集、验证集、测试集；通常设置比例为：训练集65％～75％，验证集10％～20％，测试集10％～20％，本实施例中，设置比例为训练集70％，验证集15％，测试集15％。

5)选取合适的神经网络结构进行学习拟合，当误差低于设定阈值，训练结束，获得单粒子瞬态电流源模型。

采用多层前馈神经网络进行学习拟合，学习算法采用levenberg–marquardt算法。该多层前馈神经网络包含输入层、至少一个隐藏层、输出层。通常隐藏层越多，拟合精度越高。每个隐藏层、输出层均包括至少一个神经元，神经元个数越多，精度越高。拟合误差的设定阈值采用均方误差为0.0001。

隐藏层采用tansig函数作为传输函数；输出层采用pureline函数作为传递函数；隐藏层和输出层函数具体公式见式(1)、式(2)：

fpureline(x)＝x(2)

在本发明的优选实施例中，采用8×8×1的多层前馈网络作为单粒子瞬态电流源模型，网络如图4所示，包含2层隐藏层，每层包含8个神经元，1层输出层，包含一个神经元。隐藏层采用tansig函数作为传输函数，输出层采用pureline函数作为传递函数，误差阈值采用均方误差为0.0001，学习算法采用levenberg–marquardt算法。由于输入层由时间、线性能量转移(let)、漏极偏置电压构成，输入变量的单位不同，因此在输入层与隐藏层之间引入归一化操作，同理，在输出层之后引入去归一化操作。

通过多次学习迭代最终获得基于神经网络回归的单粒子瞬态电流源模型，如图5所示，在1000次学习迭代之后，将得到的单粒子瞬态电流源模型与tcad仿真结果进行比较，可见在不同的let和漏极偏置条件下，每组单粒子瞬态电流源模型测试曲线与tcad仿真的漏极瞬态电流脉冲曲线的拟合精度较高。

以上仅是对本发明的优选实施方式进行了描述，并非对本发明技术方案的限制，本领域技术人员在本发明主要技术构思的基础上所作的任何公知变形都属于本发明所要保护的技术范畴。