一种基于多元经验模态分解的变压器顶层油温预测方法与流程

1.本发明属于变压器顶层油温预测领域，具体来说，涉及一种基于多元经验模态分解的预测方法。


背景技术：

2.电力系统是一个包含了从发电、输电、配电直到用电的完整全过程，其中变压器在完整电力系统中担当着重要的角色，是电网的心脏，它可以实现能量的转换以及电压的变换。随着特高压建设规模的扩大，电网所面临故障和事故的风险也不断扩大。一旦变压器发生事故，将会对生产生活造成严重影响，带来难以衡量的生命财产损失。油浸式变压器顶层油温是变压器热点温度的重要指标，直接影响变压器运行寿命和负载能力。为了确保变压器的安全稳定运行，彻底消除和减少变压器的潜在性故障与运行故障，提前预测油浸式变压器顶层油温成为需要研究的课题。
3.在油温预测方面，热路模型是较传统的油温预测方法，该方法需要详细的设备参数和运行参数，泛化能力不强；传统的机器学习方法例如bp、svm、决策树、贝叶斯等方法原理简单、容易操作，但当数据维度较多时预测精度不够，无法反映准确规律等问题。同时变压器油温数据具有非线性、不稳定等特点，在使用传统时间序列预测方法或神经网络预测时并不能达到理想的效果。
4.目前国内大部分变电站都安装了顶层油温油温监测装置，以变压器顶层油温作为判断依据，当顶层油温大于85度时，在线监测装置才发出警告，或进一步采取报警、跳闸等一系列保护动作。如果能提前预测主变顶层油温，通过预测值与实际监测值做对比，可以提前发现主变异常，确保主变安全运行。


技术实现要素：

5.本发明的目的在于提供一种考虑电气变量和环境影响因素，基于python语言的基于多元经验模态分解的变压器顶层油温预测方法。
6.本发明的技术解决方案是：
7.一种基于多元经验模态分解的变压器顶层油温预测方法，基于python程序设计语言，其特征在于，基于多元经验模态分解的变压器顶层油温预测方法，其具体步骤如下：
8.步骤一：导入主变电气变量和当地环境变量
9.步骤二：计算主变油温与其他变量的相关性系数，对输入变量进行数据维度筛选，筛除不相关的变量；
10.计算主变顶层油温与其他变量的相关性，筛除低相关性的变量，相关分正相关和负相关关，相关系数绝对值小于0.3为不相关；
[0011][0012]
cov(x，y)为协方差，σ
x
，σ
y
为标准差，x为x1～x
n
的均值，y为y1～y
n
的均值；
[0013]
步骤三：对筛选出来的时间序列数据共同进行多元经验模态分解法memd多元分解得到一系列频率由高到低的多元固有模态函数imf1、imf2、
…
、imf
n
和一个残余序列res；
[0014]
(1)设n维的输入序列向量其中t为输入序列的长度，方向向量集为
[0015]
(2)在(n
‑
1)维球面上设置均匀采样点集，即得到n维空间的方向向量；
[0016]
(3)计算多输入序列v(t)在各个方向的映射其中j∈{1,2,...j}；
[0017]
(4)计算与映射信号相对应的极值点的瞬时时刻h∈{1,2,...h}；
[0018]
(5)采用多元样条插值法对极值点进行差值操作，进而得到j个包络线
[0019]
(6)计算多元信号的局部均值
[0020]
(7)计算输入多维序列v(t)与m(t)的差值h(t)，并判断差值是否符合imf的判定标准，若满足则将差值h(t)从原始序列中移除的信号作为第三步的输入，重复步骤(3)～(4)，若不符合判定规则，则将d(t)作为第三步的输入，重复步骤(3)～(4)；原始多元序列v(t)可依据memd算法分解为：
[0021]
式中d表示分解得到的多元imf层数，h(t)代表n组信号imf，r(t)代表n个残量；
[0022]
步骤四：对子序列进行归一化处理，利用自注意力层sam和lstm完成预测，得到一系列的预测值f0，f1，
…
，f
n
‑1；
[0023]
(1)子序列数据归一化预处理，得到{x0,x1,
…
x
n
‑1}作为输入；
[0024]
(2)利用自注意力机制为每个序列分配权重{w0,w1,
…
w
n
‑1}，对所有时间步级状态进行加权得到{w0x0,w1x1,
…
w
n
‑1x
n
‑1}，作为lstm的输入最终用于时间序列分析预测，权重进行误差前向传播进行更新，得到预测值f0，f1，
…
，f
n
‑1；
[0025]
步骤五：将各个子序列的预测值再进行反归一化，综合叠加，得到最终预测结果；
[0026]
步骤五：将各个子序列的预测值再进行反归一化，综合叠加，得到最终预测结果；
[0027]
步骤六：通过均方误差mse、平均绝对百分比误差mape、r方r squared评价指标来衡量算法的优劣；y
i
表示真实值，表示预测值，n表示样本个数；
[0028][0029][0030]
[0031]
mse值越小，mape值越小，r2越接近1，预测能力越好，精确度越高；
[0032]
对应的一次线性回归分析图，横坐标表示预测值，纵坐标表示真实值；若假设一次方程为y＝ax+b，a代表方程的斜率，当a接近于1时代表预测值与真实值差距越小；用线性相关系数r2表示线性相关程度，当r2接近于1时，表示x和y的线性相关程度越高。
[0033]
有益效果：与现有技术相比，本发明具有以下优点：
[0034]
(1)能够对预测方法进行自我评价，衡量算法的好坏。
[0035]
(2)能够处理非线性、不稳定的序列数据，当数据维度较高时也能够准确预测。
[0036]
(3)针对所有电压等级的变压器，无需变压器的设备参数，泛化能力强，运用历史监测的电气数据和环境数据实现预测，预测准确度极高。
附图说明
[0037]
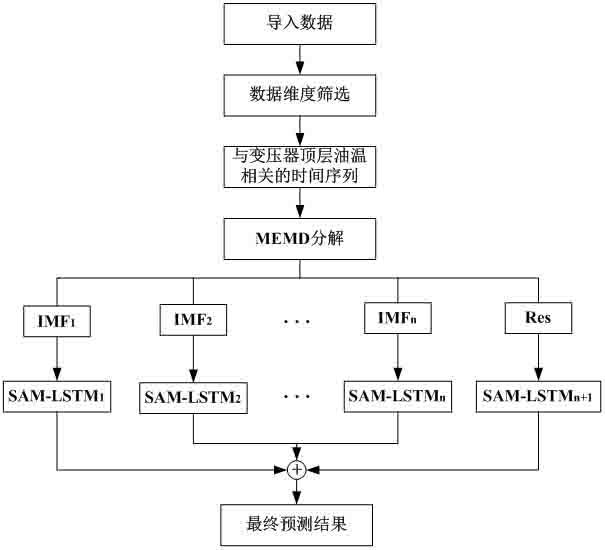
图1为本发明的流程图。
[0038]
图2主变220kv侧负荷电流memd分解结果图。
[0039]
图3海安地区环境温度memd分解结果图。
[0040]
图4海安地区空气相对湿度memd分解结果图。
[0041]
图5主变顶层油温memd分解结果图。
[0042]
图6memd的各分量预测结果图。
[0043]
图7memd
‑
sam
‑
lstm预测结果图。
[0044]
图8memd
‑
sam
‑
lstm预测方法线性回归图。
[0045]
下面结合附图，对优选实例进行详细说明。应该强调的是，下述说明仅仅是示例性的，而不是为了限制本发明的范围及其应用。
具体实施方式
[0046]
一种基于多元经验模态分解的变压器顶层油温预测方法，包括如下步骤：
[0047]
步骤一：导入主变电气变量和当地环境变量
[0048]
步骤二：计算主变油温与其他变量的相关性系数，对输入变量进行数据维度筛选，筛除不相关的变量。
[0049]
计算主变顶层油温与其他变量的相关性，筛除低相关性的变量，相关分正相关和负相关关，相关系数绝对值小于0.3为不相关。
[0050][0051]
cov(x，y)为协方差，σ
x
，σ
y
为标准差，x为x1～x
n
的均值，y为y1～y
n
的均值。
[0052]
步骤三：对筛选出来的时间序列数据共同进行多元经验模态分解法memd多元分解得到一系列频率由高到低的多元固有模态函数imf1、imf2、
…
、imf
n
和一个残余序列res。
[0053]
(1)设n维的输入序列向量其中t为输入序列的长度，方向向量集为
[0054]
(2)在(n
‑
1)维球面上设置均匀采样点集，即得到n维空间的方向向量；
[0055]
(3)计算多输入序列v(t)在各个方向的映射其中j∈{1,2,...j}；
[0056]
(4)计算与映射信号相对应的极值点的瞬时时刻h∈{1,2,...h}；
[0057]
(5)采用多元样条插值法对极值点进行差值操作，进而得到j个包络线
[0058]
(6)计算多元信号的局部均值
[0059]
(7)计算输入多维序列v(t)与m(t)的差值h(t)，并判断差值是否符合imf的判定标准，若满足则将差值h(t)从原始序列中移除的信号作为第三步的输入，重复步骤(3)～(4)，若不符合判定规则，则将d(t)作为第三步的输入，重复步骤(3)～(4)。原始多元序列v(t)可依据memd算法分解为：
[0060]
式中d表示分解得到的多元imf层数，h(t)代表n组信号imf，r(t)代表n个残量。
[0061]
步骤四：对子序列进行归一化处理，利用自注意力层sam和lstm完成预测，得到一系列的预测值f0，f1，
…
，f
n
‑1。
[0062]
(1)子序列数据归一化预处理，得到{x0,x1,
…
x
n
‑1}作为输入；
[0063]
(2)利用自注意力机制为每个序列分配权重{w0,w1,
…
w
n
‑1}，对所有时间步级状态进行加权得到{w0x0,w1x1,
…
w
n
‑1x
n
‑1}，作为lstm的输入最终用于时间序列分析预测，权重进行误差前向传播进行更新，得到预测值f0，f1，
…
，f
n
‑1。
[0064]
步骤五：将各个子序列的预测值再进行反归一化，综合叠加，得到最终预测结果。
[0065]
步骤六：通过均方误差mse、平均绝对百分比误差mape、r方r squared评价指标来衡量算法的优劣。y
i
表示真实值，表示预测值，n表示样本个数。
[0066][0067][0068][0069]
mse值越小，mape值越小，r2越接近1，预测能力越好，精确度越高。
[0070]
对应的一次线性回归分析图，横坐标表示预测值，纵坐标表示真实值。若假设一次方程为y＝ax+b，a代表方程的斜率，当a接近于1时代表预测值与真实值差距越小。用线性相关系数r2表示线性相关程度，当r2接近于1时，表示x和y的线性相关程度越高。
[0071]
以江苏省220kv海安变电站1号主变为例，最高电压等级为220kv。
[0072]
1、导入主变电气变量和当地环境变量
[0073]
数据导入从2019年8月27日到2019年9月18日共553条变压器时间序列数据。，电气变量主要为变压器最高电压等级220kv侧负荷电流、电压，环境因素变量主要为海安当地相对湿度、环境温度、瞬时风速，风级、气压能见度等，按照7：3的比例分为训练集和测试集。
[0074]
2、数据维度筛选
[0075]
把电气变量，环境因素变量跟主变油温进行相关性分析，相关系数绝对值小于0.3为不相关，筛除低相关性的电压、瞬时风速、风级、气压和能见度，数据中包含4个特征量，分别为最高电压等级220kv侧负荷电流、环境温度、空气湿度和油温。
[0076]
表1相关系数表
[0077][0078]
3、使用python3.8解释器(64位)，同时输入4个维度的序列，多元经验模态分解memd算法将多输入序列分解为8个固有模态函数(imf1～imf8)和一个残量(res)，负荷电流分解结果如图2所示。环境温度分解结果如图3所示，空气相对湿度分解结果如图4所示，主变顶层油温分解结果如图5所示。
[0079]
4、对子序列进行归一化处理，将由memd算法分解得到的8个imf分量和1个res分量输入sam
‑
lstm模型中，各子序列的预测结果如图6所示。从图中可以看出高频子序列的预测误差较大，随着频率的降低，各分量的预测值与实际值的拟合度越来越好。
[0080]
5、将各个子序列的预测值再进行反归一化，由各序分量的预测结果等权相加，即可得到基于memd
‑
sam
‑
lstm组合预测模型的预测结果。如图7所示，实线表示真实值，虚线表示预测值，从图中可以直观地发现采用多元经验模态分解方法分解后的序列再输入sam
‑
lstm模型后获得的预测数据与真实数据接近度高，模型拟合度好。
[0081]
6、评价指标如表2所示。
[0082]
表2模型预测指数
[0083][0084]
通过一次线性回归分析，分析结果如图8，图中为memd
‑
sam
‑
lstm算法线性回归参数统计表如表3所示。
[0085]
表3线性回归分析参数
[0086][0087]
从表中可以看出，采用memd
‑
sam
‑
lstm预测算法的线性回归斜率a与接近与1，同时其对应的线性相关系数r2为0.976接近于1的，预测准确度极高。
[0088]
基于python平台的算例，该发明具有以下特点：
[0089]
(1)故本方法具有优越的预测能力和更精确的预测精度。本方法简单快捷，在没有主变设备参数的情况下，可以根据历史运行数据，准确预测油温。
[0090]
(2)对原始时间序列先进行分解，再对分解后的子序列进行预测，综合叠加得到最终的预测结果，能够处理非线性、不稳定的时间序列数据。
[0091]
(3)能够对预测方法进行自我评价，衡量算法的好坏。
[0092]
最后应该说明的是，结合上述实施例仅说明本发明的技术方案而非对其限制。所属领域的普通技术人员应当理解到，本领域技术人员可以对本发明的具体实施方式进行修改或者等同替换，但这些修改或变更均在申请待批的权利要求保护范围之中。