一种乘用车下摆臂瞬态疲劳分析方法及设备与流程

本申请涉及疲劳计算技术领域，特别涉及一种乘用车下摆臂瞬态疲劳分析方法及设备。

背景技术：

目前，悬架系统作为汽车系统中重要的组成部分，是保证行驶安全性的重要部件，悬架系统技术状况、稳定性的好坏，对汽车性能的发挥和车辆在极限状态下的安全都有着重要的影响，也是目前用于衡量汽车质量的重要指标之一。下摆臂作为悬架系统的重要组成零件之一，若下摆臂在使用过程中一旦发生断裂或失效，那将会带来非常严重的后果，所以，在产品设计阶段对下摆臂结构的耐久性能分析预测变得尤为重要。

相关技术中，已有较多的汽车厂商对下摆臂耐久性能进行了分析预测，目前常用的方法通常为惯性释放方法，采用惯性释放方法计算下摆臂耐久性能方法如下所示：

(1)通过多体动力学分解的方法获得下摆臂在各个连接点处的载荷谱；

(2)建立下摆臂有限元模型，计算下摆臂在单位载荷下的应力结果；

(3)将单位载荷下的应力乘以对应通道下的载荷谱并进行矢量求和获得下摆臂的时间应力曲线；

(4)通过雨流计数法对下摆臂应力循环计算，并根据材料的s-n曲线计算下摆臂的寿命。

惯性释放方法作为有限元静力学分析的一个高级应用方法，简单地说就是用结构的惯性力来平衡外力，分析时假设零件处于一种“静态”的平衡状态，采用惯性释放功能进行静力分析时需要对一个节点进行6个自由度的约束，即虚支座，针对该支座，程序首先计算在外力作用下每个节点在每个方向上的加速度，然后将加速度转化为惯性力反向施加到每个节点上，由此构造一个平衡的力系，求解得到的位移描述所有节点相对于该支座的相对运动。上述方法主要应用于具有恒加速的设备或零件上，例如飞机在匀加减速飞行时，轮船在匀加减速航行时。然而汽车下摆臂在汽车行驶过程中会围绕车身端安装铰接出现较大幅度的往复转动，并且转动幅值和速度都是随机的，并不适用于惯性释放计算的前提条件，继续采用上述该方法预测耐久性能会导致其与实际存在较大的差距，误差很大，也不适用。

技术实现要素：

本申请实施例提供一种乘用车下摆臂瞬态疲劳分析方法及设备，以解决相关技术中使用惯性释放方法针对汽车下摆臂计算时计算结果与实际结果误差较大的问题。

第一方面，提供了一种乘用车下摆臂瞬态疲劳分析方法，其步骤包括：

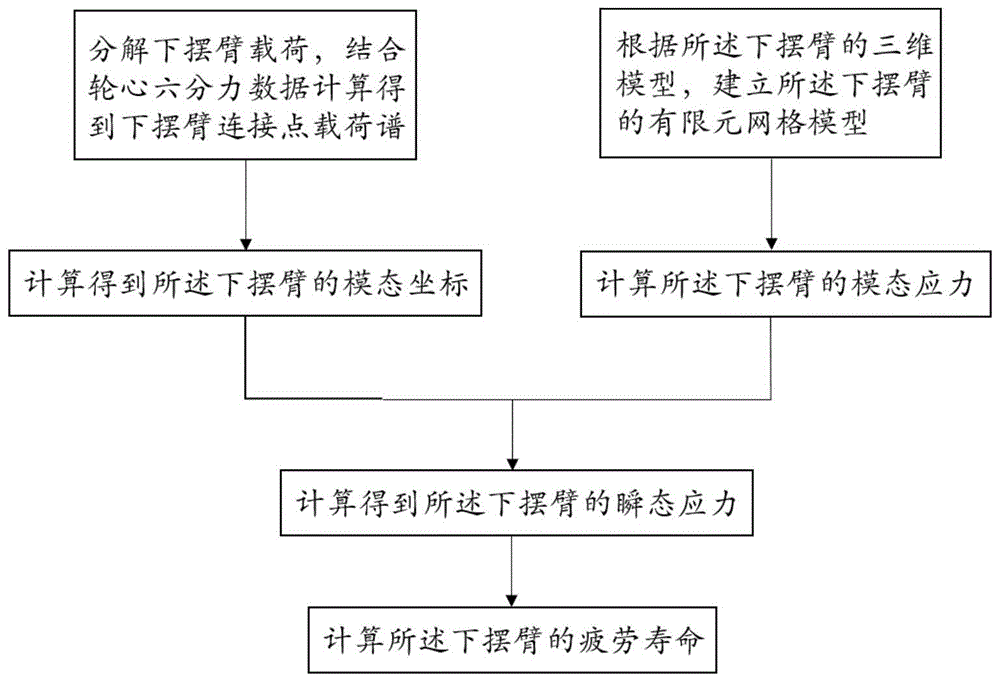
分解下摆臂载荷，结合轮心六分力数据计算得到下摆臂连接点载荷谱；

利用所述下摆臂连接点载荷谱计算得到所述下摆臂的模态坐标；

根据所述下摆臂的三维模型，建立所述下摆臂的有限元网格模型，以计算所述下摆臂的模态应力；

利用所述模态应力和模态坐标计算得到所述下摆臂的瞬态应力；

基于所述瞬态应力计算所述下摆臂的疲劳寿命。

一些实施例中，所述分解下摆臂载荷，结合轮心六分力数据计算得到下摆臂连接点载荷谱，包括：

建立整车多体动力学模型；

生成白噪声信号，利用所述白噪声信号驱动所述整车多体动力学模型，以获得所述整车多体动力学模型的逆传递函数；

利用所述逆传递函数和轮心六分力数据计算得到下摆臂连接点载荷谱。

一些实施例中，所述利用所述逆传递函数和轮心六分力数据计算得到下摆臂连接点载荷谱，包括：

通过汽车试验车耐久综合路面测试采集得到所述轮心六分力数据；

将所述轮心六分力数据和减震器测量位移信号作为期望信号，结合所述逆传递函数通过迭代得到轮心驱动位移信号；

利用所述轮心驱动位移信号驱动所述整车多体动力学模型，计算得到所述下摆臂连接点载荷谱。

一些实施例中，所述利用所述下摆臂连接点载荷谱计算得到所述下摆臂的模态坐标，包括：将所述下摆臂连接点载荷谱带入模态瞬态响应计算方程，计算得到所述下摆臂的模态坐标。

一些实施例中，所述基于所述瞬态应力计算所述下摆臂的疲劳寿命，包括：

对所述下摆臂的瞬态应力进行计数，以获取每个所述瞬态应力幅值下的循环次数；

获取材料的s-n疲劳曲线，利用所述瞬态应力幅值下的循环次数和所述s-n疲劳曲线计算所述下摆臂的疲劳寿命。

一些实施例中，所述对所述下摆臂的瞬态应力进行计数，包括：利用雨流循环计数法对所述下摆臂的瞬态应力进行雨流统计计数。

一些实施例中，所述获取材料的s-n疲劳曲线，包括：通过输入材料的抗拉强度直接生成所述s-n疲劳曲线。

一些实施例中，所述利用所述瞬态应力幅值下的循环次数和所述s-n疲劳曲线计算所述下摆臂的疲劳寿命，包括：将所述瞬态应力幅值下的循环次数与所述s-n疲劳曲线做对比统计，利用femfat软件计算得到所述下摆臂的疲劳寿命。

一些实施例中，所述下摆臂的有限元网格模型包括下摆臂有限元实体模型和rbe2刚性单元。

第二方面，提供了一种计算机设备，所述计算机设备包括处理器、存储器、以及存储在所述存储器上并可被所述处理器执行的计算机程序，其中所述计算机程序被所述处理器执行时，实现上述的乘用车下摆臂瞬态疲劳分析方法的步骤。

本申请提供的技术方案带来的有益效果包括：

本申请实施例提供了一种乘用车下摆臂瞬态疲劳分析方法，通过分解下摆臂载荷，结合轮心六分力数据计算得到下摆臂连接点载荷谱，并根据下摆臂的三维模型，建立下摆臂的有限元网格模型，以对下摆臂进行瞬态响应分析和模态分析，从而计算得到下摆臂的模态坐标和模态应力，利用模态应力和模态坐标计算得到下摆臂的瞬态应力，最后基于瞬态应力计算下摆臂的疲劳寿命。本乘用车下摆臂瞬态疲劳分析方法避开了传统的使用单位载荷法的计算缺陷，使得预测的结果与实际结果之间差距较小，使得计算的结果更加准确。

附图说明

为了更清楚地说明本申请实施例中的技术方案，下面将对实施例描述中所需要使用的附图作简单地介绍，显而易见地，下面描述中的附图仅仅是本申请的一些实施例，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据这些附图获得其他的附图。

图1为本申请实施例提供的乘用车下摆臂瞬态疲劳分析方法的流程图；

图2为本申请实施例提供的下摆臂的有限元网格模型示意图；

图3为本申请实施例提供的乘用车下摆臂瞬态疲劳分析方法中生成的白噪声信号示意图；

图4为本申请实施例提供的下摆臂的耐久计算结果图；

图5为本申请实施例根据basquin方程绘制的s-n曲线图。

具体实施方式

为使本申请实施例的目的、技术方案和优点更加清楚，下面将结合本申请实施例中的附图，对本申请实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例是本申请的一部分实施例，而不是全部的实施例。基于本申请中的实施例，本领域普通技术人员在没有做出创造性劳动的前提下所获得的所有其他实施例，都属于本申请保护的范围。

本申请实施例提供了一种乘用车下摆臂瞬态疲劳分析方法，其能解决相关技术中使用惯性释放方法针对汽车下摆臂计算时计算结果与实际结果误差较大的问题。

参见图1和图2所示，本乘用车下摆臂瞬态疲劳分析方法的步骤具体包括：首先分解下摆臂载荷，结合轮心六分力数据计算得到下摆臂连接点载荷谱，再利用下摆臂连接点载荷谱计算得到下摆臂的模态坐标，其次根据下摆臂的三维模型，建立下摆臂的有限元网格模型，以计算得到下摆臂的模态应力，最后利用模态应力和模态坐标计算得到下摆臂的瞬态应力，再基于瞬态应力计算下摆臂的疲劳寿命。其中，下摆臂的有限元网格模型包括下摆臂有限元实体模型和rbe2刚性单元。

进一步的，分解下摆臂载荷，结合轮心六分力数据计算得到下摆臂连接点载荷谱的步骤具体包括：先建立整车多体动力学模型，再生成白噪声信号，并利用白噪声信号驱动整车多体动力学模型，以获得整车多体动力学模型的逆传递函数，最后利用逆传递函数和轮心六分力数据计算得到下摆臂连接点载荷谱。

其中，这里的整车多体动力学模型包括但不限于以下零件：动力总成质量模型、白车身柔性体模型、前悬架刚柔耦合模型、后悬架刚柔耦合模型、附件配重信息等。这里，前悬架刚柔耦合模型中的前托架和稳定杆为柔性体，后悬架刚柔耦合模型中的后托架、稳定杆为柔性体。需要注意的是，搭建完成的整车多体动力学模型的前后轴荷参数、整车质心位置，重量和转动惯量参数的误差均需要控制在5％以内，衬套刚度参数和柔性体刚度参数的误差均应控制在10％以内。

进一步的，利用逆传递函数和轮心六分力数据计算得到下摆臂连接点载荷谱的步骤具体包括：首先通过汽车试验车耐久综合路面测试采集得到轮心六分力数据，然后将轮心六分力数据和减震器测量位移信号作为期望信号，结合逆传递函数通过迭代得到轮心驱动位移信号，最后利用轮心驱动位移信号驱动整车多体动力学模型，计算得到下摆臂连接点载荷谱。

具体的，参见图3所示，其为生成的白噪声信号示意图，利用白噪声信号驱动整车多体动力学模型后获得的整车多体动力学模型的逆传递函数的公式为：

其中，上述公式(1)中，ynoise为噪声信号，unoise为噪声位移，f为传递函数，通过传递函数f即可求得逆传递函数。

具体的，将轮心六分力数据和减震器测量位移信号作为期望信号，结合逆传递函数通过迭代得到轮心驱动位移信号的计算公式为：

u0＝f^-1ydesired

un+1＝un+f^-1(ydesired-yn)(2)

其中，上述公式(2)中，f¹为逆传递，ydesired为期望信号，yn为第n步迭代信号，un为第n步迭代位移。

具体的，迭代完成生成轮心驱动位移信号，利用轮心驱动位移信号驱动整车多体动力学模型，计算动力学方程后得到下摆臂连接点载荷谱，其中，动力学方程为：

其中，公式(3)中t为系统功能，q为系统广义矩阵，q为广义力矩阵，ρ为对应于完整约束的拉氏成子阵列，μ为对应于非完整约束的拉氏成子阵列。

具体的，根据下摆臂的有限元网格模型计算得到下摆臂的模态应力的公式为：

通过公式(4)可以求解下摆臂的模态变形和模态应力，其中，公式(4)中的[m]为质量矩阵，[k]{u}为位移矩阵。

进一步的，利用下摆臂连接点载荷谱计算得到下摆臂的模态坐标的步骤具体包括：将下摆臂连接点载荷谱带入模态瞬态响应计算方程，计算得到下摆臂的模态坐标，其中，模态瞬态响应计算方程为：

其中，公式(5)中的[φ]^t[m][φ]为模态质量矩阵，[φ]^t[k][φ]为模态刚度矩阵，[φ]^t{p}为模态力矢量，{ξ}为需要计算的模态坐标。

具体的，利用模态应力和模态坐标计算得到下摆臂的瞬态应力的公式为：

{σ}＝[φσ]·{q}(6)

其中，公式(6)中[φσ]为模态应力矩阵，{q}为模态坐标，{σ}为瞬态应力。

进一步的，基于瞬态应力计算下摆臂的疲劳寿命的具体步骤包括：首先对下摆臂的瞬态应力进行计数，以获取每个瞬态应力幅值下的循环次数，然后获取材料的s-n疲劳曲线，利用瞬态应力幅值下的循环次数和s-n疲劳曲线计算下摆臂的疲劳寿命。

进一步的，对下摆臂的瞬态应力进行计数具体步骤包括：利用雨流循环计数法对下摆臂的瞬态应力进行雨流统计计数。

具体的，通过雨流循环计数法对下摆臂节点的瞬态应力历程进行计数，把瞬态应力-时间历程样本记录转过90°，时间坐标轴竖直向下，样本记录犹如一系列屋面，雨水顺着屋面往下流，故称为雨流法。雨流法有下列规则：

(1)雨流在试验记录的起点和依此在每一个峰值的内边开始，亦即从1，2，3…等尖点开始；

(2)雨流在流到峰值处即屋檐竖直下滴，一直流到对面有一个比开始时最大值更正的最大值，或比最小值更负的最小值为止；

(3)当雨流遇到来自上面屋顶流下的雨时，就停止流动；

(4)如果初始应变为拉应变，顺序的始点是拉应变最小值的点；

(5)每一雨流的水平长度是作为该应变幅值的半循环进行计数的。

进一步的，参见图4所示，通过输入材料的抗拉强度即可直接生成s-n疲劳曲线，将得到的瞬态应力幅值下的循环次数与s-n疲劳曲线做对比统计，利用femfat软件计算得到下摆臂的疲劳寿命。

具体的，参见图5所示，根据basquin方程绘制材料的s-n疲劳曲线，通过输入材料的抗拉强度即可直接生成s-n疲劳曲线，对应的公式为：

sa＝s′f(2nf)^b(7)

其中，公式(7)中的s′f为疲劳强度系数，b为疲劳强度指数。

本乘用车下摆臂瞬态疲劳分析方法通过分解下摆臂载荷，结合轮心六分力数据计算得到下摆臂连接点载荷谱，并根据下摆臂的三维模型，建立下摆臂的有限元网格模型，以对下摆臂进行瞬态响应分析和模态分析，从而计算得到下摆臂的模态坐标和模态应力，利用模态应力和模态坐标计算得到下摆臂的瞬态应力，最后基于瞬态应力计算下摆臂的疲劳寿命。本乘用车下摆臂瞬态疲劳分析方法避开了传统的使用单位载荷法的计算缺陷，使得预测的结果与实际结果之间差距较小，使得计算的结果更加准确。

本申请还提供了一种计算机设备，该计算机设备包括处理器、存储器、以及存储在存储器上并可被处理器执行的计算机程序，其中计算机程序被处理器执行时，可以实现上述的乘用车下摆臂瞬态疲劳分析方法的步骤，具体步骤如下：

分解下摆臂载荷，结合轮心六分力数据计算得到下摆臂连接点载荷谱；

利用下摆臂连接点载荷谱计算得到下摆臂的模态坐标；

根据下摆臂的三维模型，建立下摆臂的有限元网格模型，以计算下摆臂的模态应力；

利用模态应力和模态坐标计算得到下摆臂的瞬态应力；

基于瞬态应力计算下摆臂的疲劳寿命。

进一步的，分解下摆臂载荷，结合轮心六分力数据计算得到下摆臂连接点载荷谱，包括：

建立整车多体动力学模型；

生成白噪声信号，利用白噪声信号驱动整车多体动力学模型，以获得整车多体动力学模型的逆传递函数；

利用逆传递函数和轮心六分力数据计算得到下摆臂连接点载荷谱。

进一步的，利用逆传递函数和轮心六分力数据计算得到下摆臂连接点载荷谱，包括：

通过汽车试验车耐久综合路面测试采集得到轮心六分力数据；

将轮心六分力数据和减震器测量位移信号作为期望信号，结合逆传递函数通过迭代得到轮心驱动位移信号；

利用轮心驱动位移信号驱动整车多体动力学模型，计算得到下摆臂连接点载荷谱。

进一步的，利用下摆臂连接点载荷谱计算得到下摆臂的模态坐标，包括：将下摆臂连接点载荷谱带入模态瞬态响应计算方程，计算得到下摆臂的模态坐标。

进一步的，基于瞬态应力计算下摆臂的疲劳寿命，包括：

对下摆臂的瞬态应力进行计数，以获取每个瞬态应力幅值下的循环次数；

获取材料的s-n疲劳曲线，利用瞬态应力幅值下的循环次数和s-n疲劳曲线计算下摆臂的疲劳寿命。

进一步的，对下摆臂的瞬态应力进行计数，包括：利用雨流循环计数法对下摆臂的瞬态应力进行雨流统计计数。

进一步的，获取材料的s-n疲劳曲线，包括：通过输入材料的抗拉强度直接生成s-n疲劳曲线。

进一步的，利用瞬态应力幅值下的循环次数和s-n疲劳曲线计算下摆臂的疲劳寿命，包括：将瞬态应力幅值下的循环次数与s-n疲劳曲线做对比统计，利用femfat软件计算得到下摆臂的疲劳寿命。

进一步的，下摆臂的有限元网格模型包括下摆臂有限元实体模型和rbe2刚性单元。

在本申请的描述中，需要说明的是，术语“上”、“下”等指示的方位或位置关系为基于附图所示的方位或位置关系，仅是为了便于描述本申请和简化描述，而不是指示或暗示所指的装置或元件必须具有特定的方位、以特定的方位构造和操作，因此不能理解为对本申请的限制。除非另有明确的规定和限定，术语“安装”、“相连”、“连接”应做广义理解，例如，可以是固定连接，也可以是可拆卸连接，或一体地连接；可以是机械连接，也可以是电连接；可以是直接相连，也可以通过中间媒介间接相连，可以是两个元件内部的连通。对于本领域的普通技术人员而言，可以根据具体情况理解上述术语在本申请中的具体含义。

需要说明的是，在本申请中，诸如“第一”和“第二”等之类的关系术语仅仅用来将一个实体或者操作与另一个实体或操作区分开来，而不一定要求或者暗示这些实体或操作之间存在任何这种实际的关系或者顺序。而且，术语“包括”、“包含”或者其任何其他变体意在涵盖非排他性的包含，从而使得包括一系列要素的过程、方法、物品或者设备不仅包括那些要素，而且还包括没有明确列出的其他要素，或者是还包括为这种过程、方法、物品或者设备所固有的要素。在没有更多限制的情况下，由语句“包括一个……”限定的要素，并不排除在包括所述要素的过程、方法、物品或者设备中还存在另外的相同要素。

以上所述仅是本申请的具体实施方式，使本领域技术人员能够理解或实现本申请。对这些实施例的多种修改对本领域的技术人员来说将是显而易见的，本文中所定义的一般原理可以在不脱离本申请的精神或范围的情况下，在其它实施例中实现。因此，本申请将不会被限制于本文所示的这些实施例，而是要符合与本文所申请的原理和新颖特点相一致的最宽的范围。