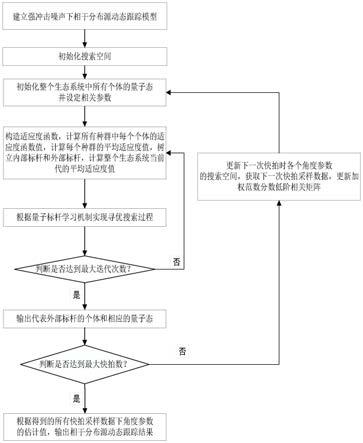
一种强冲击噪声下相干分布源动态跟踪方法

1.本发明涉及一种强冲击噪声下相干分布源动态跟踪方法，特别是一种强冲击噪声环境下的基于量子标杆学习机制的相干分布源动态跟踪方法，属于阵列信号处理领域。


背景技术：

2.近年来，高分辨率的阵列信号处理技术备受关注，尤其是阵列测向技术，在地震探测、雷达、无源声纳、无线通信等诸多领域得到广泛应用，并形成了许多高分辨率估计算法。绝大多数些波达方向估计算法大多假设信号源是远场的点目标，点目标模型是实际环境的一种近似，多数测向算法往往假设背景噪声为高斯噪声,且高速瞬时采样时角度为定值，利用二阶或高阶累积量进行分析可以获得理想的结果。然而,由于目标的尺寸取决于与阵列接受天线的距离，加之多径效应、散射等现象的影响，无线移动通信中信号波达角常在一定范围内被展开，呈现出分布信号源，同时在实际环境中分布源中心方位角是随时间变化的，而且有非高斯噪声的存在，如海杂波噪声、大气噪声、无线信道噪声等，这些噪声的模型可表示成sαs随机过程,它与高斯噪声模型失配,使得传统的基于二阶或高阶累积量的算法失效，根据分布源的散射特性，可以将其分为相干分布源和非相干分布源两类，因此研究在强冲击噪声下基于量子标杆学习机制的相干分布源动态跟踪方法具有重要的意义和价值。
3.使用极大似然算法进行相干分布源动态跟踪，可以获得高精度高分辨的跟踪性能，且可以分辨相干信源，但是需要对多维非线性优化问题进行全局最值搜索，如何快速高精度得到搜索结果是极大似然动态跟踪方法应用的经典问题，使用智能优化算法对其求解是一种具有潜力的解决方案，但现有的智能优化算法在求解复杂动态跟踪问题时又存在一些不足，如收敛速度慢、易陷入局部极值等，因此需要针对具体问题设计新的智能优化算法进行求解。
4.通过对现有技术文献的检索发现，蔡睿妍等在《电子与信息学报》(2020,42(11):2600
‑
2606),上发表的“脉冲噪声下基于相关熵的相干分布源doa估计新方法”中提出基于广义相关熵的doa估计新方法，此方法在冲击噪声环境下表现出一定的鲁棒性，但不能实现相干分布源动态跟踪，且不能分辨相干信源；guo xiansheng等在cie radar(2006:1407
‑
1410)上发表的“fast doa tracking of coherently distributed sources based on subspace updating”中提出了一种基于子空间更新的相干分布源中心doa跟踪方法,并对past算法进行改进,研究了基于fapi的动态doa估计方法，该方法具有计算量小，实时性好的特点。但是该方法在低信噪比和强冲击噪声环境下效果不理想且不能分辨相干信源。
5.已有文献的检索结果表明，现有的相干分布源动态跟踪方法多采用子空间跟踪及迭代的方法，此类算法实时性好且计算量小，但大多不能直接对相干信源进行求解，并且在低信噪比和冲击噪声的环境下性能较差，现有的相干分布源动态跟踪方法在强冲击噪声和低信噪比背景下性能恶化且不能分辨相干信源的技术难题亟待解决。


技术实现要素：

6.针对上述现有技术，本发明要解决的技术问题是提供一种强冲击噪声下相干分布源动态跟踪方法，此方法利用量子标杆学习机制进行高效求解，在强冲击噪声环境下具有鲁棒性，且可以分辨相干信源，突破了现有相干分布源动态跟踪方法的一些应用局限。
7.为解决上述技术问题，本发明的一种强冲击噪声下相干分布源动态跟踪方法，包括以下步骤：
8.步骤一：建立相干分布源的广义阵列流型，获取阵列接收信号的快拍采样数据，构造基于加权范数分数低阶相关矩阵的极大似然跟踪方程；
9.步骤二：初始化搜索空间；
10.步骤三：初始化整个生态系统中所有个体量子态并设定参数；
11.步骤四：构造适应度函数，计算所有种群中每个个体的适应度函数值，计算每个种群的平均适应度值，树立内部标杆和外部标杆，计算整个生态系统当前代的平均适应度值；
12.步骤五：根据量子标杆学习机制实现寻优搜索过程；
13.步骤六：判断是否达到最大迭代次数g，若未达到，令g＝g+1，返回步骤五；若达到则中止循环迭代，输出代表外部标杆的个体和量子态并进入下一步；
14.步骤七：判断是否达到最大快拍数k
p
，若未达到，令k＝k+1，更新下一次快拍时2p个角度参数的搜索空间，获取下一次快拍采样数据，更新加权范数分数低阶相关矩阵，返回步骤三；否则，进行下一步；
15.步骤八：根据得到的所有快拍采样数据下角度参数的估计值，输出相干分布源动态跟踪结果。
16.本发明还包括：
17.1.步骤一中建立相干分布源的广义阵列流型，获取阵列接收信号的快拍采样数据，构造基于加权范数分数低阶相关矩阵的极大似然跟踪方程具体为：
18.相干分布源的阵列接收信号模型满足：
19.x(t)＝b(ψ)s(t)+n(t)
20.其中，b(ψ)＝[b(ψ1),b(ψ2),
…
,b(ψ
p
)]为相干分布源的广义阵列流型矩阵，d为均匀线阵阵元间距，λ为相干分布源传播波长，p＝1,2,
…
,p，p为分布源个数，m为接收阵元数；θ
p
和δ
p
分别表示第p个相干分布源的中心方位角度和角度扩散；
[0021]
构造第k次快拍基于更新后加权范数分数低阶相关矩阵的极大似然跟踪方程为其中p
b(ψ)
＝b(ψ)[b
h
(ψ)b(ψ)]
‑1b
h
(ψ)为广义阵列流形矩阵b(ψ)的投影矩阵，上标h为矩阵共轭转置，argmax()表示寻找具有最大函数值的变量，trace表示对矩阵求迹。
[0022]
2.步骤二中初始化搜索空间具体为：第k次快拍时，定义2p个角度参数的搜索空间为其中，前p个u
q
(k)和v
q
(k)分别为第k次快拍第q个中心方位角搜索空间的上限和下限，q＝1,2,
…
,p，后p个u
q
(k)和v
q
(k)分别为第k次快拍第q
‑
p个角度扩散
搜索空间的上限和下限，q＝p+1,p+2,
…
,2p，第1次快拍时搜索空间的初始值分别取相应搜索空间定义域的上限和下限。
[0023]
3.步骤三中初始化整个生态系统中所有个体量子态并设定参数具体为：
[0024]
首先设定整个生态系统中的种群数目为n
p
，第φ个种群中个体的数目为n
φ
，对于第k次快拍数据，最大迭代次数其中，ζ为正整数，为向下取整函数，在第g次迭代中，第φ个种群中第个个体在2p维搜索空间中的量子态为其中，φ＝1,2,
…
,n
p
,当g＝1时，初代所有个体量子态的每一维初始化为[0,1]之间的均匀随机数；
[0025]
4.步骤四中构造适应度函数，计算所有种群中每个个体的适应度函数值，计算每个种群的平均适应度值，树立内部标杆和外部标杆，计算整个生态系统当前代的平均适应度值具体为：
[0026]
第g次迭代中，根据映射规则将所有种群中每个个体量子态的每一维映射到角度参数搜索空间范围内，得到第g次迭代第φ个种群中第个个体为其中，φ＝1,2,
…
,n
p
，q＝1,2,
…
,2p，第g次迭代第φ个种群中第个个体的适应度函数为根据适应度函数计算每个种群中所有个体的适应度函数值，计算第g次迭代第φ个种群的平均适应度值其中，φ＝1,2,
…
,n
p
，找出并记录第g次迭代第φ个种群中具有最佳适应度函数值的个体为其量子态为其中，φ＝1,2,
…
,n
p
，将其树立为内部标杆，记录并更新第g次迭代整个生态系统中具有最佳适应度函数值的个体为其量子态为将其树立为外部标杆，计算整个生态系统在第g次迭代的平均适应度值其中，φ＝1,2,
…
,n
p
。
[0027]
5.步骤五中根据量子标杆学习机制实现寻优搜索过程具体为：
[0028]
步骤5.1：所有种群中的个体进行外部标杆学习并进行适应度函数计算和评价，具体步骤为：第g代中第φ个种群中第个个体的外部学习率为其中，g’r
表示外部学习率的初始值，代表第g代中第φ个种群的平均适应度值，代表第g代中第φ个种群中第个个体的适应度函数值，φ＝1,2,
…
,n
p
，如果则第φ个种群中第个个体量子旋转角矢量为其中，为[0,1]之间均匀分布的随机数，λ0为进行外部标杆学习时的学习因子，使用模拟量
子旋转门更新量子态：其中代表第g+1代中第φ个种群中第个体第q维量子旋转角，其中，φ＝1,2,
…
,n
p
，q＝1,2,
…
,2p，之后将更新后的个体量子态映射为更新的个体然后所有个体进行适应度函数的计算和评价；
[0029]
步骤5.2：所有经过外部标杆学习后的个体进行适应度函数计算和评价后，如果第φ个种群中第个个体的适应度函数值没有得到改善，则进行内部标杆学习并进行适应度函数评价，具体步骤为：第g代中第φ个种群中第个个体的内部学习率为其中，b
r
'表示内部学习率的初始值，为第g代中第φ个种群中第个个体量子态与内部标杆的欧氏距离，即r为搜索空间的直径，即其中，代表第g代中第φ个种群内部标杆的第q维量子态，代表第g代中第φ个种群中第个个体第q维量子态，φ＝1,2,
…
,n
p
，q＝1,2,
…
,2p，如果则第φ个种群中第个个体量子旋转角矢量为其中，为[0,1]之间均匀分布的随机数，λ1为进行内部标杆学习时的学习因子，使用模拟量子旋转门更新量子态：其中代表第g+1代中第φ个种群中第个个体第q维量子旋转角，φ＝1,2,
…
,n
p
，q＝1,2,
…
,2p，之后将更新后的量子态映射为更新的个体为然后所有个体进行适应度函数的计算和评价；
[0030]
步骤5.3：所有经过内部标杆学习后的个体进行适应度函数计算和评价后，如果第φ个种群中第个个体的适应度函数值没有得到改善，则进行自我学习并进行适应度函数评价，具体步骤为：第φ个种群中第个个体的自我学习率为其中，s
r
'表示自我学习率的初始值，代表第g代中第φ个种群的平均适应度值，代表第g代中第φ个种群中第个个体的适应度函数值，φ＝1,2,
…
,n
p
，如果则进行logistic混沌映射，即其中，λ2为logistic参数，λ2∈[0,4]，φ＝1,2,
…
,n
p
，q＝1,2,
…
,2p，之后将更新后的量子态映射为更新的个体然后所有个体进行适应度函数的计算和评价；
[0031]
步骤5.4：计算更新后每个种群的平均适应度值其中，φ＝1,2,
…
,n
p
，找出并记录第g+1迭代第φ个种群中具有最佳适应度函数值的个体
其量子态为其中，φ＝1,2,
…
,n
p
，将其树立为新的内部标杆，记录并更新第g+1迭代整个生态系统中具有最佳适应度函数值的个体其量子态为将其树立为新的外部标杆，计算整个生态系统更新后的平均适应度值其中，φ＝1,2,
…
,n
p
，如果与上一代相比，平均适应度值没有得到改善或外部标杆没有发生改变，则各个种群之间相互交换具有最佳适应度函数值的个体和对应的量子态，即各种群重新树立新的内部标杆。
[0032]
6.步骤七中判断是否达到最大快拍数k
p
，若未达到，令k＝k+1，更新下一次快拍时2p个角度参数的搜索空间，获取下一次快拍采样数据，更新加权范数分数低阶相关矩阵具体为：
[0033]
判断是否达到最大快拍数k
p
，若未达到，更新k+1次快拍时2p个角度参数的搜索空间间其中，为收敛常数，μ
q
(k)为第k次快拍第q个角度参数搜索区间的中心值，即快拍第q个角度参数搜索区间的中心值，即为遗传因子，为搜索区间的搜索半径，为k
‑
1次快拍第q个角度参数的估计值，q＝1,2,
…
,2p；获取k+1次快拍采样数据x(k+1)＝[x1(k+1),x2(k+1),
…
,x
m
(k+1)]
t
，则k+1采样数据的加权无穷范数归一化信号可以表示为其中，β∈[0.8,1]为加权常数，则第k次采样数据构造的加权范数分数低阶相关矩阵增量可以表示为其中，r
m
(k+1)＝[r
1m
(k+1),r
2m
(k+1),
…
,r
mm
(k+1)]
t
，m＝1,2,
…
,m，第i行第l列元素其中，t为低阶常量，t∈[1,2]，i＝1,2,
…
,m，l＝1,2,
…
,m，上标*代表共轭；构造接收第k+1次快拍采样数据后加权范数分数低阶相关矩阵的更新方程r
s
(k+1)＝ωr
s
(k)+(1
‑
ω)r(k+1)，其中，r
s
(k)为第k次快拍采样数据更新后的加权范数分数低阶相关矩阵，r(k+1)为第k+1次接收快拍采样数据的加权范数分数低阶相关矩阵增量，ω为更新因子，令k＝k+1。
[0034]
本发明的有益效果：针对现有相干分布源动态跟踪方法的缺点和不足，本发明提出一种在强冲击噪声下基于量子标杆学习机制的相干分布源动态跟踪方法，其具体是在强
冲击噪声下设计了一种加权范数分数低阶相关矩阵，在此基础上设计基于加权范数低阶相关矩阵的极大似然动态跟踪方法进行相干分布源动态跟踪，并通过量子标杆学习机制快速得到跟踪结果，与现有技术相比，本发明具有以下优点：
[0035]
(1)针对现有相干分布源动态跟踪方法在强冲击噪声环境下性能恶化的问题，设计了更具鲁棒性的基于量子标杆学习机制的相干分布源动态跟踪方法，在强冲击噪声下设计了加权范数分数低阶相关矩阵，并利用极大似然跟踪方法实现了动态跟踪。
[0036]
(2)本发明设计的相干分布源动态跟踪方法设计了加权范数分数低阶相关矩阵，能够分辨相干信源，在强冲击噪声下实现了对动态目标的有效跟踪，设计的量子标杆学习机制可以对加权范数分数低阶相关矩阵极大似然方程进行高精度求解，快速准确的得到跟踪结果。
[0037]
(3)仿真实验证明了强冲击噪声下基于量子标杆学习机制的相干分布源动态跟踪方法的有效性，突破了传统方法在强冲击噪声和低信噪比环境下性能恶化甚至失效且不能分辨相干信源的应用局限，相对于传统的求解方法精度更高。
附图说明
[0038]
图1是本发明所设计的强冲击噪声下相干分布源动态跟踪方法示意图。
[0039]
图2是α＝0.8，广义信噪比gsnr＝20db时所设计方法对单个相干分布源中心方位角的动态跟踪结果。
[0040]
图3是α＝0.8，广义信噪比gsnr＝20db时所设计方法对单个相干分布源角度扩散的动态跟踪结果。
[0041]
图4是α＝0.8，广义信噪比gsnr＝20db时已有方法对单个相干分布源中心方位角的动态跟踪结果。
[0042]
图5是α＝1.5，广义信噪比gsnr＝15db时所设计方法对两个独立信源中心方位角的动态跟踪结果。
[0043]
图6是α＝1.5，广义信噪比gsnr＝15db时已有方法对两个独立信源中心方位角的动态跟踪结果。
[0044]
图7是α＝2，广义信噪比gsnr＝15db时所设计方法对三个独立信源中心方位角的动态跟踪结果。
[0045]
图8是α＝2，广义信噪比gsnr＝15db时已有方法对三个独立信源中心方位角的动态跟踪结果。
[0046]
图9是α＝2，广义信噪比snr＝15db时所设计方法对三个相干信源中心方位角的动态跟踪结果。
[0047]
图10是α＝2，广义信噪比snr＝15db时已有方法对三个相干信源中心方位角的动态跟踪结果。
具体实施方式
[0048]
下面结合说明书附图和具体实施方式对本发明做进一步说明。
[0049]
结合图1，本发明包括以下步骤：
[0050]
步骤一，建立相干分布源的广义阵列流型，获取阵列接收信号的快拍采样数据，构
造基于加权范数分数低阶相关矩阵的极大似然跟踪方程。
[0051]
分布源的阵列接收信号模型可以描述为角信号密度函数在分布空间积分的形式，即：其中，x(t)为分布源的阵列接收信号，a(θ)为阵列导向矢量，θ表示分布源信号所处的方向，s
p
(θ
‑
θ
p
,t)为第p个分布源的角信号密度函数，n(t)为噪声矢量，p为分布源个数。对于相干分布源模型，角信号密度函数可以表示为随机信号幅度与分布源的空间分布函数乘积的形式，即：s
p
(θ
‑
θ
p
,t)＝s
p
(t)g
p
(θ
‑
θ
p
)，其中，s
p
(t)为随机信号幅度，g
p
(θ
‑
θ
p
)为分布源的空间分布函数。假设相干分布源的空间分布函数为高斯分布，即：其中，δ
p
为未知角分布参数，则有，其中，ψ
p
＝(θ
p
,δ
p
)代表第p个相干分布源的角度参数，θ
p
和δ
p
分别表示第p个相干分布源的中心方位角度和角度扩散，则可以建立相干分布源的广义阵列流型及阵列接收信号模型，即：x(t)＝b(ψ)s(t)+n(t)，其中，b(ψ)＝[b(ψ1),b(ψ2),
…
,b(ψ
p
)]为相干分布源的广义阵列流型矩阵，d为均匀线阵阵元间距，λ为相干分布源传播波长，p＝1,2,
…
,p，m为接收阵元数。
[0052]
定义最大快拍数为k
p
，假设阵列有p个波长为λ的相干分布源入射到由m个阵元组成的均匀线阵上，则均匀线阵接收的第k次快拍数据可以表示为x(k)＝b(ψ)s(k)+n(k)，其中，k＝1,2,
…
,k
p
，b(ψ)＝[b(ψ1),b(ψ2),
…
,b(ψ
p
)]为m
×
p维广义阵列流型，第p个广义导向矢量为p＝1,2,
…
,p，x(k)＝[x1(k),x2(k),
…
,x
m
(k)]
t
为m
×
1维阵列快拍数据，其中k为快拍次数，s(k)＝[s1(k),s2(k),
…
,s
p
(k)]
t
为p
×
1维信号，n(k)为m
×
1维服从特征指数为α的标准sαs分布的复冲击噪声，j为复数单位，t为矩阵转置。
[0053]
第k次快拍采样数据的加权无穷范数归一化信号可以表示为其中，β∈[0.8,1]为加权常数，则第k次采样数据构造的加权范数分数低阶相关矩阵增量可以表示为其中，r
m
(k)＝[r
1m
(k),r
2m
(k),
…
,r
mm
(k)]
t
，m＝1,2,
…
,m，第i行第l列元素其中，t为低阶常量，t∈[1,2]，i＝1,2,
…
,m，l＝1,2,
…
,m，上标*代表共轭。r
s
(k)为第k次快拍采样数据更新后的加权范数分数低阶相关矩阵，第1次快拍时，r
s
(1)＝r(1)。构造第k次快拍基于更新后加权
范数分数低阶相关矩阵的极大似然跟踪方程为其中p
b(ψ)
＝b(ψ)[b
h
(ψ)b(ψ)]
‑1b
h
(ψ)为广义阵列流形矩阵b(ψ)的投影矩阵，上标h为矩阵共轭转置，argmax()表示寻找具有最大函数值的变量，trace表示对矩阵求迹。
[0054]
步骤二，初始化搜索空间
[0055]
第k次快拍时，定义2p个角度参数的搜索空间为其中，前p个u
q
(k)和v
q
(k)分别为第k次快拍第q个中心方位角搜索空间的上限和下限，q＝1,2,
…
,p，后p个u
q
(k)和v
q
(k)分别为第k次快拍第q
‑
p个角度扩散搜索空间的上限和下限，q＝p+1,p+2,
…
,2p。第1次快拍时搜索空间的初始值分别取相应搜索空间定义域的上限和下限。
[0056]
步骤三，初始化整个生态系统中所有个体量子态并设定相关参数。
[0057]
首先设定整个生态系统中的种群数目为n
p
,第φ个种群中个体的数目为n
φ
，对于第k次快拍数据，最大迭代次数其中，ζ为正整数，为向下取整函数。在第g次迭代中，第φ个种群中第个个体在2p维搜索空间中的量子态为其中，φ＝1,2,
…
,n
p
,当g＝1时，初代所有个体量子态的每一维初始化为[0,1]之间的均匀随机数。
[0058]
步骤四，构造适应度函数，计算所有种群中每个个体的适应度函数值，计算每个种群的平均适应度值，树立内部标杆和外部标杆，计算整个生态系统当前代的平均适应度值。
[0059]
第g次迭代中，根据映射规则将所有种群中每个个体量子态的每一维映射到角度参数搜索空间范围内，得到第g次迭代第φ个种群中第个个体为其中，φ＝1,2,
…
,n
p
，q＝1,2,
…
,2p。第g次迭代第φ个种群中第个个体的适应度函数为根据适应度函数计算每个种群中所有个体的适应度函数值，计算第g次迭代第φ个种群的平均适应度值其中，φ＝1,2,
…
,n
p
，找出并记录第g次迭代第φ个种群中具有最佳适应度函数值的个体为其量子态为其中，φ＝1,2,
…
,n
p
，将其树立为内部标杆，记录并更新第g次迭代整个生态系统中具有最佳适应度函数值的个体为其量子态为将其树立为外部标杆，计算整个生态系统在第g次迭代的平均适应度值其中，φ＝1,2,
…
,n
p
。
[0060]
步骤五，根据量子标杆学习机制实现寻优搜索过程，具体步骤为：
[0061]
(1)所有种群中的个体进行外部标杆学习并进行适应度函数计算和评价。具体步骤为：第g代中第φ个种群中第个个体的外部学习率为其
中，g
r
'表示外部学习率的初始值，代表第g代中第φ个种群的平均适应度值，代表第g代中第φ个种群中第个个体的适应度函数值，φ＝1,2,
…
,n
p
，如果则第φ个种群中第个个体量子旋转角矢量为其中，为[0,1]之间均匀分布的随机数，λ0为进行外部标杆学习时的学习因子。使用模拟量子旋转门更新量子态：其中代表第g+1代中第φ个种群中第个个体第q维量子旋转角，其中，φ＝1,2,
…
,n
p
，q＝1,2,
…
,2p，之后将更新后的个体量子态映射为更新的个体然后所有个体进行适应度函数的计算和评价。
[0062]
(2)所有经过外部标杆学习后的个体进行适应度函数计算和评价后，如果第φ个种群中第个个体的适应度函数值没有得到改善，则进行内部标杆学习并进行适应度函数评价。具体步骤为：第g代中第φ个种群中第个个体的内部学习率为其中，b
r
'表示内部学习率的初始值，为第g代中第φ个种群中第个个体量子态与内部标杆的欧氏距离，即r为搜索空间的直径，即其中，代表第g代中第φ个种群内部标杆的第q维量子态，代表第g代中第φ个种群中第个个体第q维量子态，φ＝1,2,
…
,n
p
，q＝1,2,
…
,2p。如果则第φ个种群中第个个体量子旋转角矢量为其中，为[0,1]之间均匀分布的随机数，λ1为进行内部标杆学习时的学习因子。使用模拟量子旋转门更新量子态：其中代表第g+1代中第φ个种群中第个个体第q维量子旋转角，φ＝1,2,
…
,n
p
，q＝1,2,
…
,2p。之后将更新后的量子态映射为更新的个体为然后所有个体进行适应度函数的计算和评价。
[0063]
(3)所有经过内部标杆学习后的个体进行适应度函数计算和评价后，如果第φ个种群中第个个体的适应度函数值没有得到改善，则进行自我学习并进行适应度函数评价。具体步骤为：第φ个种群中第个个体的自我学习率为其中，s
r
'表示自我学习率的初始值，代表第g代中第φ个种群的平均适应度值，代表第g代中第φ个种群中第个个体的适应度函数值，φ＝1,2,
…
,n
p
，如果则进行logistic混沌映射，即其中，λ2为logistic参数，λ2∈[0,4]，φ＝1,2,
…
,n
p
，q＝1,2,
…
,2p，之后将更新后的
量子态映射为更新的个体然后所有个体进行适应度函数的计算和评价。
[0064]
(4)计算更新后每个种群的平均适应度值其中，φ＝1,2,
…
,n
p
，找出并记录第g+1迭代第φ个种群中具有最佳适应度函数值的个体其量子态为其中，φ＝1,2,
…
,n
p
，将其树立为新的内部标杆，记录并更新第g+1迭代整个生态系统中具有最佳适应度函数值的个体其量子态为将其树立为新的外部标杆，计算整个生态系统更新后的平均适应度值其中，φ＝1,2,
…
,n
p
。如果与上一代相比，平均适应度值没有得到改善或外部标杆没有发生改变，则各个种群之间相互交换具有最佳适应度函数值的个体和对应的量子态，即各种群重新树立新的内部标杆。
[0065]
步骤六，判断是否达到最大迭代次数g，若未达到，令g＝g+1，返回步骤五；若达到则中止循环迭代，输出代表外部标杆的个体和量子态并进入下一步。
[0066]
步骤七，判断是否达到最大快拍数k
p
，若未达到，令k＝k+1，更新下一次快拍时2p个角度参数的搜索空间，获取下一次快拍采样数据，更新加权范数分数低阶相关矩阵，返回步骤三；否则，进行下一步。具体步骤为：
[0067]
判断是否达到最大快拍数k
p
，若未达到，更新k+1次快拍时2p个角度参数的搜索空间
[0068]
其中，为收敛常数，μ
q
(k)为第k次快拍第q个角度参数搜索区间的中心值，即为遗传因子，为搜索区间的搜索半径，为k
‑
1次快拍第q个角度参数的估计值，q＝1,2,
…
,2p。获取k+1次快拍采样数据x(k+1)＝[x1(k+1),x2(k+1),
…
,x
m
(k+1)]
t
，则k+1采样数据的加权无穷范数归一化信号可以表示为其中，β∈[0.8,1]为加权常数，则第k次采样数据构造的加权范数分数低阶相关矩阵增量可以表示为其中，r
m
(k+1)＝[r
1m
(k+1),r
2m
(k+1),
…
,r
mm
(k+1)]
t
，m＝1,2,
…
,m，第i行第l列元素其中，t为低阶常量，t∈[1,2]，i＝1,2,
…
,m，l＝1,
2,
…
,m，上标*代表共轭。构造接收第k+1次快拍采样数据后加权范数分数低阶相关矩阵的更新方程r
s
(k+1)＝ωr
s
(k)+(1
‑
ω)r(k+1)，其中，r
s
(k)为第k次快拍采样数据更新后的加权范数分数低阶相关矩阵，r(k+1)为第k+1次接收快拍采样数据的加权范数分数低阶相关矩阵增量，ω为更新因子，令k＝k+1，返回步骤三；否则，执行步骤八。
[0069]
步骤八，根据得到的所有快拍采样数据下角度参数的估计值，输出相干分布源动态跟踪结果。
[0070]
在图2、图3、图5、图7和图9中，本发明所设计的基于量子标杆学习机制的相干分布源动态跟踪方法记作qboa
‑
inf
‑
ml；图4、图6、图8和图10中所涉及的方法来自cie radar(2006:1407
‑
1410)上发表的“fast doa tracking of coherently distributed sources based on subspace updating”，记作fapi
‑
tls
‑
esprit。
[0071]
基于量子标杆学习机制的相干分布源动态跟踪方法的仿真实验参数设置如下：均匀线阵的阵元数为m＝8，阵元间距d＝0.5λ，k
p
＝400，种群数目n
p
＝2，每个种群的个体数为15，ξ＝5，g’r
＝0.5，b’r
＝0.5，s’r
＝0.5，λ0＝10，λ1＝3，λ2＝4，β＝1，t＝1.5，ω＝0.95。
[0072]
图2、图3和图4中相干分布源从θ1(k)＝[5cos(2πk/400)]
°
，δ1＝8
°
入射到均匀线阵，从仿真图中可以看出，在强冲击噪声下，传统方法已完全失效，所设计的方法不仅能有效的对相干分布源中心方位角进行跟踪，还可以对相干分布源角度扩散值进行跟踪。
[0073]
图5和图6中两个相干分布源分别从θ1(k)＝[50+5cos(2πk/400)]
°
，δ1＝1.5
°
，θ2(k)＝[
‑
50+5cos(2πk/400)]
°
，δ2＝3
°
入射到均匀线阵，两个相干分布源之间是相互独立的，从仿真图中可以看出，在弱冲击噪声下，所设计的方法能有效的对相干分布源中心方位角进行跟踪，表现出优于传统方法的跟踪性能。
[0074]
图7和图8中三个相干分布源分别从θ1(k)＝[50+5cos(2πk/400)]
°
，δ1＝1.5
°
，θ2(k)＝[5cos(2πk/400)]
°
，δ2＝2.5
°
，θ3(k)＝[
‑
50+5cos(2πk/400)]
°
，δ3＝3.5
°
入射到均匀线阵，三个相干分布源之间是相互独立的，从仿真图中可以看出，在高斯噪声下，所设计的方法能有效的对相干分布源中心方位角进行跟踪，表现出优于传统方法的跟踪性能。
[0075]
图9和图10中三个相干分布源分别从θ1(k)＝[50+5cos(2πk/400)]
°
，δ1＝1.5
°
，θ2(k)＝[5cos(2πk/400)]
°
，δ2＝2.5
°
，θ3(k)＝[
‑
50+5cos(2πk/400)]
°
，δ3＝3.5
°
入射到均匀线阵，三个相干分布源之间是相干的，从仿真图中可以看出，在高斯噪声下，所设计的方法不仅能有效的对相干分布源中心方位角进行跟踪，表现出优于传统方法的跟踪性能，还能分辨相干信源，突破了传统方法的一些应用局限。