基于特征学习与集成学习的高维不平衡数据分类方法与流程

1.本发明涉及高维数据分类技术领域，尤其涉及一种基于特征学习与集成学习的高维不平衡数据分类方法。


背景技术：

2.随着互联网和移动智能终端的爆发式增长，在电子商务、金融科技、医疗科技、政府部门以及互联网行业等诸多领域积累了海量的数据，而这些数据背后含有大量有价值的信息，因此对这些数据进行数据挖掘(data mining，dm)也变得十分重要。其中，对数据进行有效的分类则是数据挖掘的重要方向之一。分类是指根据已有的数据特征和类别通过分类模型进行训练，不断优化分类模型之后，对没有类别的数据进行分类处理。
3.在大数据中，高维不平衡数据是十分常见的，高维数据是指数据的特征非常多，有些数据的特征能达到上千个甚至上万个，高维数据随着维度的增加，分类模型的训练难度随之加大，并且模型的性能会越来越低。而特征与类别以及特征与特征之间通常具有一定的关联，如果能够通过某种方法对这些特征进行筛选，选择只对分类有关联的特征，对分类无关的特征全部剔除，那么就能实现对高维特征进行降维处理，而特征选择方法就是其中之一。特征选择方法通过分析特征与类别的相关性和特征与特征之间的冗余性，对无关特征和冗余特征进行删除。一般采用统计学方法对相关性与冗余性进行度量，包括空间距离测量、一致性度量等等。在对高维不平衡数据进行分类时，传统的机器学习分类算法在低维平衡数据上可以进行有效分类，而这些算法无法适应数据的高维化和不平衡，因为高维特征增加了模型的分类难度，而数据的不平衡性使得分类算法偏向多数类样本，导致少数类样本的分类准确率低。而在实际应用中，少数类数据往往蕴含着价值极高的信息。比如在医疗诊断中，虽然健康人群的数量远远大于癌症病人的数量，但人们只关心癌症病人的诊断；在人脸识别中，虽然人脸识别技术越来越发达，但是依然无法对模糊脸部进行有效识别。少数类被错误分类往往会造成不可估量的损失，但目前对于高维不平衡数据的分类研究难以达到理想状态，大多只解决了数据的高维问题或者不平衡问题，某些算法虽然分类效果好，但模型的泛化能力差，无法适应大多数情形。


技术实现要素：

4.本发明的目的在于提供一种基于特征学习与集成学习的高维不平衡数据分类方法，以提高高维不平衡数据的分类准确率。
5.本发明通过下述技术方案实现：
6.基于特征学习与集成学习的高维不平衡数据分类方法，包括以下步骤：
7.s1：用混合采样算法对原始数据集进行均衡化处理，得到均衡化数据集；
8.其中，原始数据集为多个高维不平衡数据的集合；
9.s2：用特征选择算法对所述均衡化数据集进行特征选择，得到最优特征集；
10.s3：用训练好的stacking集成学习模型对所述最优特征集进行分类。
11.优选地，所述s1包括以下子步骤：
12.s11：用nenn算法剔除所述原始数据集中的噪声样本，得到无噪声数据集；
13.s12：对所述无噪声数据集中的边界样本进行过采样，得到过采样数据集；
14.s13：对所述无噪声数据集中的多数类样本进行欠采样，得到欠采样数据集；
15.s14：合并所述过采样数据集和所述欠采样数据集，得到所述均衡化数据集。
16.优选地，所述s12包括以下子步骤：
17.s121：获取所述边界样本中的多数类样本集a和少数类样本集b；
18.s122：获取所述少数类样本集b中的多数类样本集a1和少数类样本集b1；
19.s123：合并所述多数类样本集a1和所述多数类样本集a，得到多数类样本边界集；
20.s124：获取多数类样本边界集中的少数类样本b2；
21.s125：合并所述少数类样本集b1和所述少数类样本集b2，得到少数类样本边界集；
22.s126：从所述少数类样本边界集中随机选择两个样本，并按下式生成新的少数类样本；
23.x
new
＝x1+random(0，1)*(y
i
‑
x2)i＝1，2，...，n；
24.其中，x
new
表示新生成的少数类样本，x1和x2分别表示从少数类样本中随机选择的两个样本，y
i
表示k个同类最近邻按照采样倍率随机选择的第i个同类样本，n为自然数；
25.s127：循环n次所述s126，得到所述过采样数据集；n为自然数。
26.优选地，所述s13包括以下子步骤：
27.s131：用k
‑
means聚类算法将所述无噪声数据集中的多数类样本划分为k类样本，并获取每类样本的样本中心；
28.s132：计算k类样本的平均样本数，以及每个样本中心与所有样本的平均距离；
29.s133：计算每一类中的样本中心与样本的距离；
30.s134：如果样本中心与样本的距离超过平均距离，且该类中样本数量少于平均样本数，则剔除该样本，得到所述欠采样数据集。
31.优选地，所述s2包括以下子步骤：
32.s21：剔除所述均衡化数据集中的无关特征和冗余特征，得到候选特征子集；
33.s22：用c4.5分类器对所述候选特征子集中的特征进行准确率测量，剔除使得准确率降低的特征，得到最优特征子集。
34.优选地，所述s21包括以下子步骤：
35.s211：计算所述均衡化数据集中每个特征与所属类别的mic值；
36.s212：从所述均衡化数据集中剔除所述mic值小于mic阈值所对应的特征，得到特征子集；
37.s213：计算所述特征子集中每个特征与其余特征的su值和pearson值；
38.s214：根据所述su值和所述pearson值计算得到对应特征的平均值；：
39.s215：从所述特征子集中剔除所述平均值高于阈值平均值所述对应的特征，得到所述候选特征子集。
40.优选地，所述s22包括以下子步骤：
41.s221：获取所述候选特征子集中每个特征的互补性值；
42.s222：根据对应的所述互补性值的大小对所述候选特征子集中的特征进行降序排
列；
43.s223：按照排列顺序，依次选取一个特征用c4.5算法进行准确率测量；
44.s224：如果该特征使得准确率升高或不变，则保留该特征；否则，从所述候选特征子集中剔除该特征，得到所述最优特征子集。
45.优选地，所述stacking集成学习模型包括基模型层和元模型层；
46.所述基模型层，用于对所述最优特征集进行预分类，得到预测分类结果；
47.所述元模型层，用于根据所述预测分类结果得到实际的分类结果。
48.优选地，所述基模型层包括支持向量机、决策树、随机森林和自适应增强。
49.优选地，所述元模型层包括极度梯度提升树。
50.本方案结合数据的高维和不平衡特性，从混合采样、特征选择和集成学习三个方面进行了研究。首先，为了缓解数据的不平衡程度，提出了基于bn
‑
smote和kcus的混合采样算法。对边界少数类样本进行过采样，对远离聚类中心的多数类样本进行欠采样，通过与其他采样算法进行对比实验，结果表明该算法对少数类样本的分类具有良好的效果，但整体的分类准确率并不理想。于是进一步分析特征的冗余性和相关性，本方案提出了基于mic和fcbf的高维特征选择算法。在filter阶段，利用mic系数和fcbf算法剔除无关特征和冗余特征；在wrapper阶段，选择互补性高的的特征加入候选特征子集，根据c4.5分类器的分类效果对特征子集进行评估，选择最优特征子集，通过对比实验，结果表明该算法在特征选择方面的优越性。在混合采样和特征选择的基础上，为了提升模型的泛化能力和分类准确率，提出基于stacking集成学习的多模型融合算法，并选择svm、决策树、随机森林和adaboost作为基模型分类器以及xgboost作为元模型分类器，这些分类器差异性大、分类效果好，选择运行速度较快，融合后的模型能够大大提升稳定性和准确率。
51.本发明与现有技术相比，具有如下的优点和有益效果：
52.1、针对高维不平衡数据集中出现的重复、异常以及冗余等噪声问题，设计了一个新的噪声去除算法nenn，针对数据分布不平衡的特点，结合bn
‑
smote和kcus算法，对决策边界模糊的少数类样本进行过采样，合成新的少数类样本，基于k
‑
mean聚类原理，剔除远离聚类中心的多数类样本，缓解数据的不平衡程度，提高分类模型的准确度；
53.2、根据高维不平衡数据集的特征高维化的特点，设计了一种新的高维特征选择算法hfs
‑
mf，采用mic系数和fcbf算法剔除无关和冗余特征，利用c4.5分类器对特征子集进行评估，得到准确率最高的最优特征子集；
54.3、基于stacking集成学习的训练框架，选择svm、决策树、随机森林、adaboost作为基模型层的分类器，这些分类器差异性大、分类效果好，选择运行速度较快、分类效果极强的xgboost算法作为元学习器，融合后的模型能够大大提升稳定性和准确率。
附图说明
55.此处所说明的附图用来提供对本发明实施例的进一步理解，构成本申请的一部分，并不构成对本发明实施例的限定。在附图中：
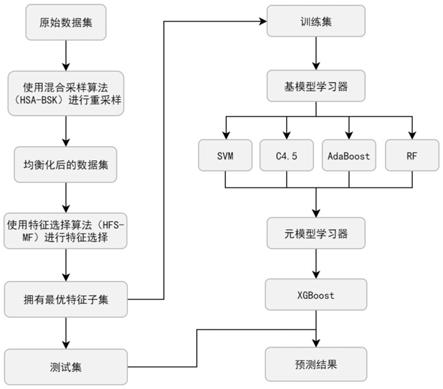
56.图1为本发明基于stacking集成学习模型融合框架图；
57.图2为本发明hsa
‑
ksr算法流程图；
58.图3为本发明三种类型的样本分布图；
59.图4为本发明kcus算法流程图；
60.图5为本发明少数类样本分布图；
61.图6为本发明hfs
‑
mf算法流程图。
具体实施方式
62.为使本发明的目的、技术方案和优点更加清楚明白，下面结合实施例和附图，对本发明作进一步的详细说明，本发明的示意性实施方式及其说明仅用于解释本发明，并不作为对本发明的限定。
63.实施例
64.基于特征学习与集成学习的高维不平衡数据分类方法，如图1所示，包括以下步骤：
65.s1：用混合采样算法对原始数据集进行均衡化处理，得到均衡化数据集，如图2所示；
66.其中，本实施例所说的原始数据集为多个高维不平衡数据的集合。
67.数据集存在噪声数据的问题是无法避免的，如果不对噪声数据进行处理，就会加大分类的难度和精度，特别是在高维不平衡数据中，边界少数类样本和噪声样本有时也会重叠，因此，在本步骤中，首先对整个原始数据集进行噪声样本预处理。
68.具体地，数据集包括边界样本(boundary)、噪声样本(noise)和安全样本(safety)三类。其中，边界样本是位于决策边界的样本，数量较少，但是位于边界的少数类样本对分类具有决定性作用；噪声样本是混入正确样本之间的数据或者位于边界区域内的数据，噪声样本会干扰分类的效果；安全样本是位于决策边界之外的样本，数量多，对边界影响较小。如图3所示，两条虚线之外的数据为安全样本，虚线上的样本为边界样本，虚线之间的样本为噪声样本。
69.为了解决噪声样本带来的影响，本方案根据数据集的分布空间，采用了nenn算法的最近邻噪声清除算法(noise edited nearest neighbor，nenn)对噪声样本进行剔除。由于噪声样本数据的分布大多集中在边界区域或者样本数据内部，因此可以通过计算每个样本点之间的欧氏距离，得到样本点的k个最近邻样本，然后分析k个最近邻样本的类别，如果k个最近邻样本中至少包括2/3的不同类样本，那么就可以将此样本点划分为噪声样本，并将其删除。具体算法步骤如下：
70.输入：原始数据集s，最近邻个数k，噪声样本集n＝[]
[0071]
输出：无噪声数据集s
e
[0072]
过程：
[0073]
遍历整个原始数据集s；
[0074]
任意选择样本点x
i
∈s；
[0075]
利用欧氏距离公式计算样本点x
i
附近的k个最近邻样本；
[0076]
如果k个最近邻样本中至少有个样本类别与样本点x
i
不同，则n＝n+x
i
；
[0077]
s
e
＝s
‑
n；
[0078]
returns
e
。
[0079]
噪声样本剔除后，然后通过bn
‑
smote过采样算法对分类难度较大的少数类样本进行过采样，以增加少数类样本数目。
[0080]
本方案中的bn
‑
smote过采样算法是在borderline
‑
smote基础上改进的，其核心思想是根据borderline
‑
smote算法思想将样本划分为安全样本、边界样本和噪声样本三类，其中噪声样本在过采样之前利用nenn算法进行了剔除，因此本步骤只有安全样本和边界样本两类。继续将边界样本划分为多数类样本a和少数类样本b，然后计算少数类样本b的最近邻，继续将少数类样本b划分为少数类样本b1和多数类样本a1，对多数类样本a和多数类样本a1进行并集操作，得到多数类边界集，然后在继续计算多数类边界集的最近邻样本，继续将多数类边界集划分为少数类样本b2和多数类样本b2，对少数类样本b1和少数类样本b2进行并集操作，这样就能得到边界最难分类的少数类样本集，从少数类样本集中n次随机选择两个样本，并按下式生成新的少数类样本，从而扩充少数类样本的数量，得到过采样样本集；
[0081]
x
new
＝x1+random(0，1)*(y
i
‑
x2)i＝12，...，n；
[0082]
其中，x
new
表示新生成的少数类样本，x1和x2分别表示从少数类样本中随机选择的两个样本，y
i
表示k个同类最近邻按照采样倍率随机选择的第i个同类样本，n为自然数，其取值根据实际需要合成的少数类样本数量进行确定。
[0083]
bn
‑
smote算法具体步骤如：
[0084]
输入：原始数据集s，最近邻个数k，噪声样本集n＝[]
[0085]
输出：过采样样本集s
out
[0086]
过程：
[0087]
将边界样本划分为多数类和少数类；
[0088]
对于少数类样本x
i
∈s，计算x
i
最近邻的多数类样本集s
max
(x
i
),包含k个距离最近的样本；
[0089]
对s
max
(x
i
)做并集操作，得到多数类样本的边界集s
maxj
，
[0090]
对多数类样本y
i
∈s
maxj
，计算y
i
最近邻的少数类样本集s
imaxj
(y
i
)，包含k1个距离最近的样本
[0091]
对s
imaxj
(y
i
)做并集操作，得到少数类样本的最难区分的边界集s
min
，
[0092]
从s
min
中随机选择两个样本，根据公式x
new
＝x+random(0，1)*(y
i
‑
x)i＝1，2，...，n进行合成x
new
，将x
new
添加到s
out
，循环n次；
[0093]
返回s
out
。
[0094]
在该步骤中，采用bn
‑
smote算法进行过采样，相较传统过采样算法而言，bn
‑
smote算法在边界决策方面优势很明显，能够最大程度的区分少数类样本，该算法的时间复杂度较低，选择样本的方式比较简单有效，特别是能够确定最近邻的参数k，能够达到数据均衡的目的。
[0095]
最后通过kcus欠采样算法剔除多数类样本的边缘样本，清理模糊的边界样本，使得进行分类时边界更加清晰。
[0096]
kcus算法是基于k
‑
means聚类的欠采样算法，其核心思想是根据数据集的分布特
点来进行样本选择和删除，从整体数据集的分布而言，类别相同的样本一般都是集中在一起的，相似度较高，集合程度也很高，包含的重要信息也相似，而没有聚合在附近的边缘样本与该类别的聚合程度低，并且可能与附近的其他类别的属性有相似之处，为了排除分类的干扰，对于这些离群点和边缘点进行删除，保证同属于一个类别的样本点聚集在一起，具体实现过程如图4所示。
[0097]
由图4可以看出，kcus算法的时间复杂度比较高，每次选择样本中心都需要与每个样本点进行计算，然后不断筛选出聚集程度最高的样本中心。并且对于边缘点的选择也是通过计算每个点与样本中心的距离，然后对所有距离进行均值操作，如果样本点与样本中心的距离超过平均距离并且样本个数少于平均样本数，则选择该样本点作为边缘点并进行删除。
[0098]
具体地，在本步骤中，首先用k
‑
means聚类算法将无噪声数据集中的多数类样本划分为k类样本，并获取每类样本的样本中心；其次计算k类样本的平均样本数，以及每个样本中心与所有样本的平均距离；然后计算每一类中的样本中心与样本的距离；如果样本中心与样本的距离超过平均距离，且该类中样本数量少于平均样本数，则剔除该样本，否则，保留该样本，从而得到欠采样数据集。
[0099]
对于不平衡数据的分类而言，大部分研究者更多的关注少数类样本的分布不均衡和扩大少数类样本的数量问题，因为对分类算法而言，少数类样本具有很重要的分类价值，特别是位于边界区域并且数量较少的样本。因此，对于不平衡数据的研究，如何保证少数类的样本不丢失、不产生干扰、能够有效进行数据分类是目前过采样技术面临的重点和难点。过采样和欠采样通过增加少数类样本和削减多数类样本的方式使得整个数据集达到一定的平衡，为后面分类算法的学习和训练提供有效的信息，提升识别率。如果只是单一的使用某个方法就会造成样本的整体数目发生变化，并且新增的样本和删除的样本都有可能影响整个数据集的分布，这是算法本身存在的局限性。
[0100]
通过大量的实验发现，少数类样本分布的位置无非就是以下几种情况：
[0101]
第一，分布在多数类样本的内部，这一情况一般直接将其视为噪声数据，毫无研究价值；
[0102]
第二，位于多数类与少数类的边界，这种情况是最常见的，也是最复杂的。如果处理不当，很容易将其视为干扰项直接删除或者与其它少数类混在一起，在进行过采样时，容易形成干扰。；
[0103]
第三，位于多数类的边缘并且不影响整个数据集，这类数据一般都是通过检测最近邻的类别来进行判断，如果不造成干扰，直接通过合适的方法进行样本合成，少数类样本的三种分布情况如图5所示；
[0104]
为了解决边界少数类样本的问题，本方案采用了bn
‑
smote算法进行少数类样本的新增合成，该算法最突出的优势是能够通过几次最近邻的划分，将最难学习的少数类样本区分出来，特别是位于边界决策区域的少数类样本，该算法能够有效的避免数量稀少的少数类样本直接被删除，有效解决少数类样本的重叠、类间不平衡和过拟合等问题。
[0105]
针对多数类数据集的分布特点，同类样本大都集中在一起，本方案选择了基于样本分布特点的k
‑
means聚类欠采样算法(kcus)，该算法首先随机从样本中选择k个样本中心，通过计算每个样本点与样本中心的距离，将样本划分为k类，重新计算样本中心，直到样
本中心确定。其次，计算样本中心与各个样本点的平均距离，如果样本点与样本中心的距离超过平均距离并且样本点数量少于平均样本数，则直接删除该样本点。
[0106]
本方案的hsa
‑
bsk混合采样算法是结合bn
‑
smote算法和kcus算法提出的，能够有效处理边界的少数类样本和删除边缘的多数类样本，缓解数据的不平衡性，提高分类性能。同时该算法能够克服单一的过采样或欠采样存在的缺点，通过新增少数类样本和缩减多数类样本进行数据重构，达到数据平衡的目的，对提升分类器的性能产生了有利影响。
[0107]
s2：用特征选择算法对均衡化数据集进行特征选择，得到最优特征集；
[0108]
对于高维数据的分类而言，其属性过多不仅干扰分类结果，而且会大大降低分类器的训练效率，因此筛选出最具有代表性的特征是高维数据分类的关键。根据特征与所属类别的关系可以区分特征是否与类别相关，按照特征与特征之间的关联程度，可以筛选出关联性较强的特征，进而区分特征是否冗余。其中，无关特征是指该特征对最终分类没有任何关联，冗余特征是该特征与其它特征相似度较高，部分信息出现重复。基于此，本实施例提出了基于mic和fcbf的高维特征选择算法(high
‑
dimensional feature selection algorithm based on mic and fcbf，简称hfs
‑
mf算法)。该算法分为filter和wrapper两个阶段。在filter阶段，使用mic相关系数作为评价指标，对无关和弱相关特征进行过滤，得到候选特征子集；在wrapper阶段，利用互补性作为评价指标，计算候选特征子集中每个特征的互补性值，并通过分类器对候选特征子集进行分类，得到分类准确率最高的最优特征子集。
[0109]
mic为最大信息系数，要对高维数据进行分类，最重要的一个问题就是如何降低数据的维度，而大量的属性之间存在一些重要联系，我们无法用肉眼去发掘，但是可以采用某种统计方法对这些属性进行测量，找出属性之间的关系，并根据一定的标准去选择最优的属性，从而对高维数据进行特征选择处理。而统计方法需要满足适应性(adaptability)和公平性(equitability)两个原则，公平性是指对与所属类别不同的属性中加入噪声，统计方法都能得到一样的值；适应性是指能够对线性、非线性、非单调等等函数关系和非函数关系都能进行统计测量。
[0110]
最大信息系数(max information coefficient，mic)能够对变量之间的相关性进行有效的衡量，而且具备适应性和公平性原则。mic的核心思想是利用互信息(mi)和网格划分方法，如果两个变量存在关联性，将其离散在二维空间中，并且使用散点图来表示，将当前二维空间在x，y方向分别划分为一定的区间数，然后查看当前的散点在各个方格中落入的情况，这就是联合概率的计算，这样就解决了在互信息中的联合概率难求的问题，具体计算如下所示：
[0111][0112]
其中，d是一个有序对集合，x表示将特征f的值域划分为x段，xy＜b(n)表示网格数目小于b(n)，i(d，x，y)表示不同网格划分下的mi最大值，ln(min(x，y))表示将最大mi值归一化。
[0113]
mic方法是在mi的基础上提出，弥补了mi不能衡量连续变量关系的不足，相比于其他评价指标，mic系数有着更好的稳定性、广泛性和公平性，适用于高维数据的特征选择工作。
[0114]
fcbf是一种快速关联的过滤算法，该算法使用启发式后向顺序搜索方式快速寻找最优特征子集，采用对称不确定性(symmetrical uncertainty，su)作为评价指标，每次得到最优特征并删除该特征的所有冗余特征。su广泛应用于衡量两个非线性变量的紧密程度，如特征与所属类别或者特征与特征之间的相关性，具体计算如下所示：
[0115]
h(x)＝
‑
∑
i
p(x
i
)log2(p(x
i
))；
[0116]
h(x|y)＝
‑
∑
j
p(y
i
)∑p(x
i
|y
i
)log2p(x
i
|y
i
)；
[0117]
i(x|y)＝h(x)
‑
h(x|y)＝h(y)
‑
h(y|x)；
[0118][0119]
h(x)表示变量x的信息熵，其取值具有不确定性，p(x
i
)表示事件x在第i个时间发生的概率，h(x|y)表示条件熵，变量x关于已知条件y的不确定性程度即y单独发生时，x发生的概率，p(y
i
)表示事件y在第i个时间发生的概率，p(x
i
|y
i
)表示在第i个时间在事件y发生的条件下，事件x发生的概率，i(x|y)表示互信息，衡量变量x和y的关联程度即拥有多少公共的信息，su(x，y)是衡量变量x和y不确定性程度，su在[0，1]之间取值，值越大表示关联性越强，su对mi进行了归一化处理，克服了ig在特征选择的偏向性。
[0120]
衡量特征i与类别c的关联程度记作su
i，c
，衡量特征i与特征j的关联程度记作su
i，j
，fbcf算法主要分为两个阶段：去除不相关特征和去除冗余特征。首先从原始特征集计算每个特征与类别的su值，即相关性程度，筛选大于阈值的特征集并按照su值降序排列。然后从特征子集第一个开始，如果su
i，c
＞su
i+1，i
，那么直接剔除该特征后面的特征，一直循环这个过程，直到特征集为空。通过分析可知，如果特征与类别的关联性越强，保留的可能性就越大，其特征间的相关性也相应变大。
[0121]
具体地，在本步骤中，首先计算每个特征与所属类别的mic值以及特征与特征之间的冗余度，将无关特征和部分冗余特征进行过滤，得到候选特征子集。然后计算候选特征子集的互补性，对候选特征集进行降序排列，每次选择第一个特征加入最优候选子集，计算加入前后的分类准确率，如果准确率降低则剔除该特征，如果升高或不变则加入最优特征子集，循环该过程，直到候选特征子集为空，hfs
‑
mf算法具体实现如下，如图6所示：
[0122]
1)为消除不同特征的数量影响，将均衡化数据集中的所有特征进行归一化处理(min
‑
max normalization)，即：将取值映射到[0，1]范围内，具体公式如下所示：
[0123][0124]
其中，x
i，j
′
表示均衡化数据集中第i个样本特征j归一化后的特征值，x
i，j
表示均衡化数据集中第i个样本特征j的特征值，x
j，max
和x
j，min
分别表示特征j的最大值和最小值；
[0125]
2)剔除相关性低的特征：计算均衡化数据集中每个特征与所属类别的mic值，把mic值低于mic阈值的特征剔除，然后根据mic值进行降序排列；
[0126]
其中，mic阈值的设置方式如下：
[0127]
σ＝0.4*(max(m
f
)
‑
min(m
f
))；
[0128]
其中，σ表示mic阈值，max(m
f
)和min(m
f
)分别表示特征与类别相关性的最大值和最小值，两者的差越大，说明原始特征集存在无关和弱相关特征较多，阈值变大，删除的特征也会增加；
[0129]
3)剔除冗余度高的特征：按照排列顺序，从第一个特征开始，计算每个特征与其他特征的su值和pearson值，对两个相关系数取平均值，剔除高于阈值平均值(本实施例中的阈值平均值设置为0.7)对应的特征，从而得到候选特征子集；
[0130]
4)前面两个步骤能够将大部分无关和冗余特征剔除，接下来继续剔除一些表现较差的特征：首先计算候选特征子集中每个特征的互补性值，(互补性值＝mic值/平均冗余度)并根据互补性值的大小对特征进行降序排序，然后利用c4.5算法进行准确率测量，如果加入特征之后，准确率降低，那么这个特征直接就被剔除，继续测量下一个，从而得到最优特征子集。
[0131]
在本方案中，为了得到最优特征子集，使得该最有特征子集具有互补性(complementarity)，即：含有的特征都与所属类别有较大的相关性(correlation)，并且特征与特征之间有较小的冗余性(redundancy)，本方案对相关性度量使用mic系数作为评价指标，对冗余性度量使用pearson系数和su的均值作为评价指标，对互补性度量采用相关性与冗余性的商作为评价指标，具体计算如下：
[0132][0133][0134]
其中，c
f
表示互补性，m
f
表示mic系数，r
f
表示冗余性，p
f
表示pearson系数，su
f
表示对称不确定性，c
f
从相关性和冗余性对候选特征的重要程度进行度量。
[0135]
m
f
值越大且r
f
值越小，则c
f
越大，表示该特征与所属类别的相关性高与候选特征子集的冗余性低，具有较强的互补作用。
[0136]
在现有技术中，基于filter的特征选择算法与分类器相互独立，可以快速删除一部分与类别无关或者弱相关的特征，选择的特征在不同的数据中有着不错的泛化能力，能够适应各类高维数据，但filter只针对单个特征与类别的关系，忽略了特征与特征之间的相互联系，因此可能导致重要特征被删除，而且对最后的分类结果的准确度也相对不高。基于wrapper的特征选择算法是通过分类器的分类精度来评估特征子集的优劣，能够筛选部分冗余特征，能够得到较优的特征子集，最终的分类准确率较高，但是wrapper算法是一个个特征进行冗余性分析，对于高维数据的特征选择的适应性较差，算法的效率较低，对于海量数据的分类其时间性能非常差，过拟合现象比较严重。
[0137]
fcbf算法实现简单，效率较高，能够有效删除冗余特征和无关特征，但是fcbf算法认为特征与特征的相关性强就被视为冗余特征，得到的最优特征子集和分类准确度也不如relieff算法，而且在进行无关特征的筛选方面su系数的适应性也没有mic系数强。
[0138]
为了剔除与类别之间无相关和弱相关的特征、与特征之间的冗余特征，并且要保证算法的运行速度和最终分类的效果，本方案提出了基于mic与fcbf的高维特征选择算法，该算法利用了filter算法的速度，采用了wrapper算法准确率高的特点，结合mic系数、su和pearson系数的度量方式，高效的删除无关特征和冗余特征，得到最优特征子集，相比于其他单一算法和同类型算法，在分类准确率和稳定性方面表现更加优异。
[0139]
s3：用stacking集成算法对最优特征集进行分类。
[0140]
stacking集成算法包含了两层模型：基学习器模型和元学习器模型。在本方案中，
最优特征子集通过基学习器的训练，输出一个预测分类结果，然后再将该预测分类结果作为元学习器的输入，最后得到的结果就是最终的分类结果。为了使得stacking集成算法具有最佳的预测效果，基学习器需要具备独立性高、差异性大、学习能力强以及分类性能优异的特性，而元学习器需要满足性能稳定、泛化性强以及分类效果好的特征性。因此，在本方案中，基模型层的分类器选择了支持向量机(svm)、决策树(c4.5)、随机森林(rf)以及自适应增强(adaboost)算法，元模型层将极度梯度提升树(xgboost)算法作为元学习器，如图1所示。
[0141]
svm算法对于线性可分的数据具有很好的分类效果，通过引入核函数对可以对高维数据进行简化处理，同样svm算法对于非线性数据也有着不错的分类性能；c4.5算法采用信息增益率作为分类指标，加强了对少数类样本的识别率，避免出现过拟合问题，对于不平衡数据分类有良好的效果，并且引入剪枝方法，能够减小噪声数据的干扰，简化树的结构，大大提升了分类的准确率；随机森林算法由多个决策树组成，采用自助采样的方式增加了数据子集的规模，每个学习器的差异性较大，模型泛化能力强；由于不需要进行特征选择，可以对高维数据进行有效处理，并且能够区分特征的重要程度；随机森林基于bagging思想，采用并行化方式进行训练，模型的训练速度极快。adaboost算法通过递归的方式进行学习，降低正确分类的样本权重，增加错误分类的样本权重，使得对于少数类样本和难分类样本获得更大的权重，在极其不平衡数据集分类时有着卓越的表现。xgboost算法引入正则项降低了模型的复杂度，在优化时对代价函数进行二阶泰勒展开，引入二阶导数防止模型出现过拟合问题，xgboost采用列抽样，提高了模型的计算速度，在分类性能、运算速度、容错率和稳定性都有着极强的效果。
[0142]
将多个学习器组合使用就需要一定的融合策略，目前学习器的结合策略主要是三种：投票法、平均法和学习法。
[0143]
投票法是指训练集通过个体学习器训练之后会产生一个类别的预测结果，对于每个预测结果，各个个体学习器可以独立进行投票，最后选择得票最高的结果作为类别的预测结果，而投票法可细分为：绝对多数投票法(majority voting)、相对多数投票法(plurality voting)、加权投票法(weighted voting)。绝大多数投票的思想是如果某个类别投票数超过一半，并且得票数最高，则将此结果作为分类类别。
[0144]
相对多数投票是指如果某个类别的票数最高，就将此样本的预测结果作为分类类别，如果票数最高的标记有多个，则直接随机选择一个标记。
[0145]
加权投票是指如果在投票前，根据学习器的重要程度进行加权赋值，将权重和票数相加，得到分数最高的类别作为最终类别。
[0146]
平均法就是将每个个体学习器的预测结果取平均值输出，将此均值作为最终的预测结果，平均法可分为简单平均法(simple averaging)和加权平均法(weighted averaging)。简单平均法将所有的个体学习器视为同等重要，而加权平均法则是根据预测结果的不同赋予不同的权重，学习效果越好的个体学习器其重要性越高。
[0147]
学习法是一种更为强大的融合策略，主要是将个体学习器的预测结果不直接使用投票法或者平均法处理，而是将个体学习器的输出结果作为输入，继续通过另一个强大的学习器进行训练，学习法的这种策略能够减小学习的误差，使得模型具有更好的分类性能。因此，在本实施例中采用学习法作为stacking集成算法的融合策略，以提升stacking集成
算法的稳定性和泛化能力。
[0148]
以上所述的具体实施方式，对本发明的目的、技术方案和有益效果进行了进一步详细说明，所应理解的是，以上所述仅为本发明的具体实施方式而已，并不用于限定本发明的保护范围，凡在本发明的精神和原则之内，所做的任何修改、等同替换、改进等，均应包含在本发明的保护范围之内。