一种用于求解柔性梁系统动力学方程的分裂迭代方法

1.本发明属于多柔体系统动力学领域，尤其是涉及多节相互耦合的柔性梁的动力学方程求解方法。


背景技术：

2.相互耦合的多节柔性梁系统在工程领域有着广泛的应用，比如起重机、高空作业平台的工作臂架均为相互套接或相互铰接的柔性臂结构。为了提高起重设备，尤其是高空载人作业设备的安全性、稳定性，有必要对相互耦合的多节柔性梁系统进行动力学建模及仿真求解。
3.目前，市场上的商业有限元软件尚不能对相互套接的柔性梁系统的伸缩运动及复合运动进行有效的仿真求解。在相应的工程应用场景中，对于臂架的伸缩运动，大多基于变长度梁模型进行分析求解，但这种方法要求在动态仿真过程中不断重新构造质量矩阵和刚度矩阵，增加了计算量。对于臂架的俯仰运动与回转运动，一般采用浮动坐标(floating frame of reference，ffr)方法进行建模分析，通过这种方法得到的系统的质量矩阵的元素是广义坐标的函数，导致求解较为困难。也有学者利用d
‑
h方法(denavit
‑
hartenberg method)结合商业有限元软件进行相关分析，代价是忽略了臂架的刚性运动与弹性变形之间的耦合，降低了求解精度。利用ancf(absolute nodal coordinate formulation)方法对相互套接的柔性梁系统建模可以得到梁的常数质量矩阵，但该方法具有广义坐标数目较多，求解时计算量较大的缺点。


技术实现要素：

4.针对上述柔性梁系统动力学方程求解过程中存在的问题，本发明提出一种求解方法，将柔性梁系统的部分广义坐标表示为另一部分广义坐标与lagrange乘子的taylor级数，从而减少系统方程中的变量数目，并通过迭代方式改变taylor级数的展开点，从而不断逼近柔性梁系统动力学方程的精确解。
5.柔性梁系统的静平衡方程具有如下形式：
[0006][0007]
其中，e和k分别为柔性梁系统的广义坐标向量和刚度矩阵；λ为lagrange乘子向量；f为广义力向量，其元素是e与λ的函数；∏为与e相关的约束方程组。
[0008]
柔性梁系统的动力学方程具有如下形式：
[0009][0010]
其中，为系统的广义加速度向量，为系统的广义速度向量，m为系统的质量矩阵，c为系统的阻尼矩阵。e，m，c，k，λ的元素均为时间t的函数。∏为与广义坐标e相关的约束方程组。将时间变量t进行离散，利用数值积分方法可将(2)式转化为如下的静态求解形式：
[0011][0012]
方程组(3)中，δt为时间迭代步的步长，矩阵
t+δt
k
′
与向量
t+δt
f
′
依赖于所选择的数值积分方法及上一个迭代步的结果
t
e，方程组(3)与方程组(1)具有一致的形式，故求解方法也一致。以下为求解步骤：
[0013]
1.一种用于求解柔性梁系统动力学方程的分裂迭代方法，包含如下步骤：
[0014]
s1、对系统建模，得到系统的静平衡方程(1)或动力学方程的静态求解形式(3)；
[0015]
s2、将系统的广义坐标e分裂为主坐标e
m
和从坐标e
s
两部分；
[0016]
s3、将从坐标e
s
迭代展开成主坐标e
m
和lagrange乘子λ的taylor级数；
[0017]
s4、将求得的从坐标e
s
关于主坐标e
m
和lagrange乘子λ的taylor级数代入静平衡方程(1)或动力学方程的静态求解形式(3)，减少变量数目，进而求解主坐标e
m
与lagrange乘子λ的近似解；
[0018]
s5、将s4中求得的主坐标e
m
与lagrange乘子λ代入到从坐标e
s
关于主坐标和lagrange乘子的taylor级数表达式，求得从坐标e
s
的近似解；
[0019]
s6、判断所得结果是否满足精度要求，如满足则结束迭代，如不满足则跳转至s7；
[0020]
s7、对s4与s5求得的主坐标与从坐标进行修正；
[0021]
s8、利用s7中求得的广义坐标更新系统的刚度矩阵，约束方程，广义力；
[0022]
s9、将s7中求得的主坐标e
m
与s4中求得的lagrange乘子λ设为下一轮迭代所需的taylor级数的展开点；
[0023]
s10、跳转至s3；
[0024]
2.所述步骤s1中，将(1)式中的广义坐标e分裂为两部分：一部分称为主坐标e
m
；另一部分称为从坐标e
s
。
[0025]
(1)可以改写为
[0026][0027]
3.所述步骤s2中，系统的平衡方程可写为迭代形式
[0028][0029]
方程组(4)和(5)的迭代系数矩阵k
11
与k
22
必须可逆；
[0030]
4.所述步骤s3中，将方程组(5)第1式中的从坐标迭代展开为主坐标与lagrange乘子的taylor级数；
[0031][0032]
即将从坐标e
s
展开为主坐标e
m
与lagrange乘子λ的taylor级数，将此taylor级数代入(5)第1式右边，将代入结果再展开为主坐标e
m
与lagrange乘子λ的taylor级数，如此迭代直至所求的taylor级数的系数收敛至满足精度要求。e
s
的迭代初始值可取系统在刚性构形下e
s
的取值；
[0033]
5.将求得的从坐标e
s
关于主坐标e
m
与lagrange乘子λ的taylor级数代入(5)式中第2式和第3式得：
[0034][0035]
从而减少变量数目，进而由(7)求解主坐标e
m
与lagrange乘子λ；
[0036]
6.将求得的主坐标e
m
与lagrange乘子λ的数值代入到从坐标e
s
关于主坐标和lagrange乘子的taylor级数表达式，求得从坐标e
s
的近似解；
[0037]
7.判断求得的结果是否满足求解精度，如果满足则结束求解，如果不满足则将第6步中求得的e
m
、e
s
、λ代入(5)的前两式的右边，得到新的e
m
与e
s
，并利用该结果更新刚度矩阵、质量矩阵、约束方程及广义力；
[0038]
8.将第7步中求得的主坐标e
m
与第6步中求得的lagrange乘子λ的数值作为下一轮迭代的taylor级数的展开点，即通过在迭代时变换taylor级数的展开点的方法，不断逼近函数的真实解；
[0039]
9.在求解过程中，根据边界条件的变化选取主坐标及从坐标，保证在边界条件产生变化时，系统的动力学方程组不病态。
[0040]
本发明的有益效果：
[0041]
本发明所述方法是一种二重迭代方法，包括内外两层迭代过程。在内层迭代过程中，将柔性梁系统的动力学方程中的部分广义坐标(从坐标)展开为另一部分广义坐标(主坐标)及lagrange乘子的taylor级数。在外层迭代过程中，求取主坐标与lagrange乘子的近似解，并将结果作为下一轮内层迭代的taylor级数的展开点，即通过在迭代过程中变换taylor级数的展开点的方法，不断逼近方程的真实解。该方法可以起到降低变量数目，简化方程的作用。在分裂广义坐标的同时，也分裂了广义坐标的系数矩阵，减小了求解过程中系数矩阵求逆的计算量。在求解过程中，依据边界条件变化选择主坐标与从坐标，使得系统的动力学方程组不病态，提高了数值稳定性，避免了在求解过程中，重复生成网格，重复生成系统的质量矩阵及刚度矩阵，提高求解效率。
附图说明
[0042]
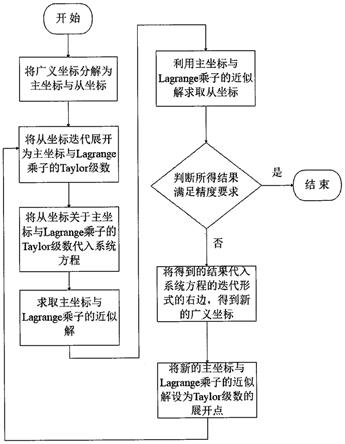
图1为摘要附图。
[0043]
图2为某型号高空作业平台的工作臂机构简图。
[0044]
图3为静态求解流程图。
[0045]
图4为动态求解流程图。
[0046]
图5为复合运动过程中基本臂的边界条件。
[0047]
图6为复合运动过程中中间臂的边界条件。
[0048]
图7为复合运动过程中前臂的边界条件。
[0049]
图8a为前臂头部加载300kg载荷时伸缩臂机构作举升回转伸出复合运动时三节臂头部节点在or1方向的位移。
[0050]
图8b为前臂头部加载300kg载荷时伸缩臂机构作举升回转伸出复合运动时三节臂头部节点在or2方向的位移。
[0051]
图8c为前臂头部加载300kg载荷时伸缩臂机构作举升回转伸出复合运动时三节臂头部节点在or3方向的位移。
[0052]
图9a为前臂头部加载300kg载荷时伸缩臂机构作举升回转伸出复合运动时三节臂
头部节点在or1方向的速度。
[0053]
图9b为前臂头部加载300kg载荷时伸缩臂机构作举升回转伸出复合运动时三节臂头部节点在or2方向的速度。
[0054]
图9c为前臂头部加载300kg载荷时伸缩臂机构作举升回转伸出复合运动时三节臂头部节点在or3方向的速度。
[0055]
图10a为前臂头部加载300kg载荷时伸缩臂机构作举升回转伸出复合运动时从第5秒至第45秒的三节臂头部节点在or1方向的加速度。
[0056]
图10b为前臂头部加载300kg载荷时伸缩臂机构作举升回转伸出复合运动时从第5秒至第45秒的三节臂头部节点在or2方向的加速度。
[0057]
图10c为前臂头部加载300kg载荷时伸缩臂机构作举升回转伸出复合运动时从第5秒至第45秒的三节臂头部节点在or3方向的加速度。
[0058]
图中：1.基本臂，2.伸缩缸，3.中间臂尾部上端滑块，4.前臂尾部上端滑块，5.基本臂头部上端滑块，6.中间臂，7.中间臂头部上端滑块，8.前臂，9.中间臂头部的伸出滑轮，10.中间臂头部下端滑块，11.钢丝绳，12.基本臂头部下端滑块，13.前臂尾部下端滑块，14.中间臂尾部下端滑块，15.变幅缸，16.回转平台，17.中间臂尾部侧滑块，18.基本臂头部侧滑块，19.前臂尾部侧滑块，20.中间臂头部侧滑块。
[0059]
该工作臂为三节伸缩臂机构。中间臂套接在基本臂内，前臂套接在中间臂内。臂与臂之间通过滑块相互支撑，通过伸缩缸与钢丝绳作为驱动，实现三节臂之间的同步伸出运动。基本臂的后铰点与回转平台铰接，前铰点与变幅缸的一端铰接，变幅缸的另一端与回转平台铰接。
具体实施方式
[0060]
下面结合实施例和附图进一步说明本发明的内容，实施例采用ancf方法及广义阿尔法方法(所选择的建模方法及数值积分方法仅为说明专利内容，本专利对建模方法及数值积分方法不作限制)对某型号高空作业平台的工作臂机构进行建模求解。
[0061]
伸缩臂机构的静态求解方法如下：
[0062]
(1)依据伸缩臂机构的实际结构，定义各节臂的形状参数及网格划分；
[0063]
(2)建立各节臂的局部坐标系、插值函数，插值矩阵；
[0064]
(3)更新伸缩臂机构中各节臂的欧拉角、刚度矩阵、广义力及静平衡方程；
[0065]
(4)将三节臂的广义坐标e
i
(i＝1，2，3)分裂为主坐标(e
i
)
m
(i＝1，2，3)与从坐标(e
i
)
s
(i＝1，2，3)两个部分，对刚度矩阵k
i
与广义力列阵f
i
亦做相应的分解，并将静平衡方程改写为迭代形式。须依据约束方程组选取主坐标，使主坐标出现在约束方程组中，且主、从坐标的迭代系数矩阵均为可逆；
[0066]
(5)在内层迭代中，将从坐标(e
i
)
s
(i＝1，2，3)迭代展开为主坐标(e
i
)
m
(i＝1，2，3)与lagrange乘子λ的taylor级数，各节臂的主坐标的展开点的迭代初始值可取为各节工作臂均为刚性构形时的值；lagrange乘子的迭代初始值λ
[0]
可取为零向量；
[0067]
(6)在外层迭代中，将从坐标关于主坐标与lagrange乘子的taylor级数代入静平衡方程组，求得主坐标与lagrange乘子λ
[n]
；
[0068]
(7)将求得的主坐标与lagrange乘子代入从坐标关于主坐标与lagrange乘子的
taylor级数，求得从坐标；
[0069]
(8)判断求得的结果是否满足求解精度，如果满足则结束求解，如果不满足则将第(6)步与第(7)步求得的主坐标、从坐标、lagrange乘子代入静平衡方程的迭代形式的右边，得到新的主坐标与从坐标
[0070]
(9)将第n轮外层迭代中得到的主坐标与lagrange乘子λ
[n]
设为第n+1轮迭代的taylor级数的展开点并跳转至第(3)步。
[0071]
伸缩臂机构的动态求解方法如下：
[0072]
(1)依据伸缩臂机构的实际结构，定义各节臂的尺寸参数及网格划分；
[0073]
(2)由ancf方法建立各节臂的局部坐标系、插值函数、插值矩阵、质量矩阵；
[0074]
(3)由静态求解方法求取伸缩臂机构的初始状态；
[0075]
(4)定义动态求解参数(数值积分方法中的积分参数及时间步长等参数)；
[0076]
(5)依据ancf方法及数值积分方法建立系统动力学方程；
[0077]
(6)增加一个时间步；
[0078]
(7)更新伸缩臂机构的欧拉角、广义坐标的系数矩阵k
′
、约束方程组∏及广义力列阵f；
[0079]
(8)将三节臂的广义坐标e
i
(i＝1，2，3)分裂为主坐标(e
i
)
m
(i＝1，2，3)与从坐标(e
i
)
s
(i＝1，2，3)两个部分，并相应地分裂广义坐标的系数矩阵k
′
i
(i＝1，2，3)与广义力列阵f
i
(i＝1，2，3)，据此将动力学方程的静态求解形式改写为迭代形式。为保证数值稳定性，须依据约束方程组选取主坐标，使其出现在约束方程组中，并且约束方程组不病态，主、从坐标的迭代系数矩阵均可逆；
[0080]
(9)将第n轮外层迭代得到的结果与λ
[n]
设为分裂迭代方法的taylor级数的展开点，主坐标的迭代初始值可取为各节工作臂均为刚性构形时的值，lagrange乘子的迭代初始值λ
[0]
可取为零向量；
[0081]
(10)在内层迭代中将从坐标迭代展开为主坐标与lagrange乘子λ
[n+1]
的taylor级数；
[0082]
(11)将从坐标关于主坐标与lagrange乘子的taylor级数代入动力学方程组，在外层迭代中求解主坐标近似解与用于下一轮迭代的lagrange乘子λ
[n+1]
；
[0083]
(12)将求得的主坐标近似解与lagrange乘子λ
[n+1]
代入从坐标关于主坐标与lagrange乘子的taylor级数，求得从坐标的近似解；
[0084]
(13)判断求解结果是否满足精度要求，是则跳转至第(16)步，否则跳转至第(14)步；
[0085]
(14)将第(11)步中求得的主坐标与从坐标的近似解及lagrange乘子λ
[n+1]
代入系统方程的迭代形式的右边，得到用于下一轮迭代的主坐标与从坐标
[0086]
(15)跳转第(7)步；
[0087]
(16)按照所选择的数值积分方法求解速度、加速度；
[0088]
(17)检查动态求解是否完成，是则结束动态求解，否则跳转至第(6)步。
[0089]
以下以举升
‑
回转
‑
伸出复合运动为例，结合附图，对本方法作具体介绍。
[0090]
举升
‑
回转
‑
伸出复合运动中，不仅各节伸缩臂之间的相对位置是时变的，而且是
空间运动，每一个广义坐标在三个坐标轴的方向上均为时变函数。同时，为了保证求解过程中的数值稳定性，主(从)坐标的选择也较为复杂。按照该型号高空作业平台的额定设置，运动过程时长设为45秒，45
‑
50秒为惯性振荡时间。
[0091]
依据静态求解方法中的步骤(1)
‑
(3)，依照机构的实际形状与尺寸，利用ancf方法对某型号高空作业平台进行建模。如图5
‑
图7所示，全局坐标系为or1r2r3。对各节臂进行网格划分。不失一般性，设三节臂各有4个网格节点a
1，i
，a
2，i
，a
3，i
，a
4，i
；i＝1，2，3。各节臂的广义坐标分别为：
[0092][0093]
系统的广义坐标向量为各节臂的刚度矩阵分别为k
i
，i＝1，2，3，系统的刚度矩阵为k＝diag(k1，k2，k3)，得到伸缩臂机构水平初始状态下的静平衡方程为：
[0094][0095]
求解初始状态，再结合广义阿尔法方法(本专利对数值积分方法不作限制)对某型号高空作业平台进行动力学建模，伸缩臂机构动力学方程的静态求解形式为：
[0096][0097]
为求解公式(9)和(10)，须选取系统的主从坐标。
[0098]
如图5所示，o2，o1分别位于基本臂前后两组铰点的连线中点。全局坐标系原点o位于基本臂的水平回转轴与o1o2水平状态时的交点。r
rot
平行于基本臂尾部铰点连线。φ
2，1
为基本臂的水平回转角。和分别为从o1，o2指向a
1，1
，a
2，1
的向量。其大小均为h。h1为水平面内后铰点连线的中点o1与全局坐标系的原点o的距离。or2为伸缩臂机构的水平回转轴。基本臂的随动坐标系为a
1，1
x1y1z1。设当伸缩臂机构作复合运动时，基本臂绕坐标轴or2转动的回转角为φ
2，1
，角速度为ω2，俯仰角为φ
3，1
，角速度为ω3。
[0099]
基本臂尾部截面处焊有加强筋及加强板件，具有足够的结构刚度，故有以下几何约束条件。
[0100]
基本臂的尾部节点a
1，1
到o1的距离为定值h，满足
[0101][0102]
基本臂尾部节点a
1，1
处的向量平行于向量三维条件下，有如下约束：
[0103][0104]
由于在运动过程中，恒不为零，故在上述三式中，可选e
1，1
、e
2，1
、e
3，1
为主坐标。
[0105]
在复合运动过程中，a
1，1
所在截面没有剪切变形，即正交于向量
[0106][0107]
由于在运动过程中，恒不为零，故可取e
5，1
为主坐标。
[0108]
在复合运动过程中，基本臂的尾部节点a
1，1
处的截面没有扭转变形和绕伸缩臂轴线的刚性转动，即向量平行于单位向量r
rot
，且正交于向量即
[0109][0110]
显然可选为基本臂的主坐标。为保证主坐标出现在约束方程中，且方程不致出现病态现象，规定：
[0111][0112]
在基本臂a
2，1
节点处，有如下约束：
[0113]
假设在复合运动过程中，基本臂a
2，1
节点处的截面不产生绕轴线的扭转，故：
[0114][0115]
同上文所述，为保证主坐标出现在约束方程中，且计算中方程系数不病态，可按如下规则选取主坐标：
[0116][0117]
基本臂a
2，1
节点处焊有加强板件，制约了运动过程中a
2，1
所在截面的扭转变形，故在复合运动过程中，有如下约束条件：
[0118]
向量正交于r
rot
＝[
‑
sin(φ
2，1
) 0 cos(φ
2，1
)]
t
：
[0119][0120]
同上文，按如下规则选取主坐标：
[0121][0122]
点o2到基本臂的轴线上的节点a
2，1
的距离为定值h：
[0123][0124]
式中，取为基本臂的主坐标。
[0125]
向量平行于向量
[0126][0127]
在运动过程中，恒不为零，故取和作为基本臂的主坐标。
[0128]
a
2，1
节点处的向量正交于向量
[0129]
e
16，1
·
e
19，1
+e
17，1
·
e
20，1
+e
18，1
·
e
21，1
＝0
ꢀꢀꢀꢀꢀ
(22)
[0130]
运动过程中，的分量恒不为零，故取为基本臂的主坐标。
[0131]
在复合运动过程中，a
2，1
节点处的向量正交于向量由于平行于r
rot
＝[
‑
sin(φ
2，1
) 0 cos(φ
2，1
)]
t
，故有：
[0132]
e
18，1
·
cos(φ
2，1
)
‑
e
16，1
·
sin(φ
2，1
)＝0
ꢀꢀꢀꢀꢀ
(23)
[0133]
按如下规则选取主坐标：
[0134]
[0135]
在基本臂头部焊有加强板，使基本臂的头部结构具有足够的抗扭转刚度，故在头部节点a
4，1
处，有约束条件：
[0136][0137]
分量形式为：
[0138]
e
43，1
·
e
46，1
+e
44，1
·
e
47，1
+e
45，1
·
e
48，1
＝0
ꢀꢀꢀꢀꢀꢀꢀꢀ
(26)
[0139]
的分量在运动过程中恒不为零，故在上式中可取为基本臂的主坐标。
[0140]
综上，基本臂的主坐标选取如下：
[0141]
如果cos2(φ
2，1
)≥sin2(φ
2，1
)，则基本臂的主坐标为：
[0142]
e
1，1
，e
2，1
，e
3，1
，e
5，1
e
9，1
，e
10，1
，e
11，1
，e
14，1
，e
15，1
，e
17，1
，e
18，1
，e
19，1
，e
21，1
，e
22，1
，e
23，1
，e
47，1
；
[0143]
如果cos2(φ
2，1
)＜sin2(φ
2，1
)，则基本臂的主坐标为：
[0144]
e
1，1
，e
2，1
，e
3，1
，e
5，1
，e
7，1
，e
11，1
，e
12，1
，e
13，1
，e
14，1
，e
16，1
，e
17，1
，e
19，1
，e
21，1
，e
23，1
，e
24，1
，e
47，1
。
[0145]
如图6所示，中间臂的随动坐标系为a
1，2
x2y222。l1为基本臂长度，l2为中间臂长度。设在t时刻，中间臂尾部节点a
1，2
与基本臂的轴线上的p1点重合，位于基本臂的第2个插值区间内，区间序号基本臂头部节点a
4，1
与中间臂的轴线上的p2点重合，位于中间臂的第2个插值区间内，区间序号中间臂尾部节点a
1，2
距离基本臂尾部节点a
1，1
的距离为l1(t)。
[0146]
对中间臂的尾部节点a
1，2
及其所在截面，有如下约束条件：
[0147]
中间臂的尾部节点a
1，2
与基本臂轴线上的点p1重合，即
[0148][0149]
e1是基本臂的广义坐标，是对应于基本臂的第个插值区间的插值矩阵。在上式中，e
k，2
(k＝1，2，3)可作为中间臂的主坐标。
[0150]
固连在中间臂尾部的上滑块和下滑块的承载面积较大，制约了中间臂尾端节点a
1，2
所在截面与基本臂轴线上的点p1所在截面的相对转动，加之侧滑块的作用，故在空间复合运动中有如下约束条件：
[0151]
点a
1，2
所在截面的向量平行于基本臂轴线上的点p1所在截面的向量
[0152][0153]
在运动过程中，恒不为零，故可取和作为中间臂的主坐标。
[0154]
a
1，2
所在截面的向量正交于同一截面的向量
[0155]
e
4，2
·
e
7，2
+e
5，2
·
e
8，2
+e
6，2
·
e
9，2
＝0
ꢀꢀꢀꢀ
(29)
[0156]
由于在运动过程中恒不为零，故可选取作为中间臂的主坐标。
[0157]
由于在中间臂尾部焊有加强板、伸缩缸等其它附件，故a
1，2
所在截面有较强的抗扭转刚度，在空间复合运动过程中不产生扭转变形，即向量正交于a
1，2
点所在截面向
量
[0158]
e
10，2
·
e
7，2
+e
11，2
·
e
8，2
+e
12，2
·
e
9，2
＝0
ꢀꢀꢀꢀ
(30)
[0159]
由于在复合运动过程中恒不为零，故在上式中，可选作为中间臂的主坐标。
[0160]
同样在t时刻，基本臂的头部节点a
4，1
与中间臂尾部的距离为l1‑
l1(t)，由此可确定a
4，1
所在的中间臂插值区间序号及插值矩阵设a
4，1
位于中间臂的第个插值区间内(图6中)，与中间臂的轴线上的p2点重合，故在基本臂头部与中间臂的搭接处，有如下约束：
[0161]
点p2与前臂头部节点a
4，1
满足：
[0162][0163]
e2是中间臂的广义坐标，是对应于中间臂的第个插值区间的插值矩阵。上式中，可取
[0164][0165]
为中间臂的主坐标。
[0166]
固连在基本臂头部的下滑块的承载面积较大，加之侧滑块的作用，制约了p2所在截面与前臂节点a
4，1
所在截面的绕向量及的相对转动。故有如下约束。
[0167]
点p2所在截面的向量平行于基本臂的a
4，1
点所在截面的向量
[0168][0169]
由于运动过程中，的分量恒不为零，可分别选取e
12k+7，2
，e
12k+9，2
，作为中间臂的主坐标。
[0170]
中间臂头部也焊接有加强板件，有较强的抗扭转刚度，故分量形式为：
[0171]
e
46，2
·
e
43，2
+e
47，2
·
e
44，2
+e
48，2
·
e
45，2
＝0
ꢀꢀꢀꢀ
(33)
[0172]
因为运动过程中，恒不为零，故在上式中，可取e
47，2
为中间臂的主坐标。
[0173]
在基本臂头部加强板件的作用下，基本臂头部有足够大的结构刚度，截面的形状保持不变，使中间臂的p2点所在截面的向量与基本臂头部节点a
4，1
点所在截面向量正交：
[0174][0175]
p2点的广义坐标是与的线性组合。为了保证主坐标出现在约束方程中，同时避免在(33)与(34)中重复选取同一个主坐标，作如下规定：
[0176][0177]
综上，中间臂的主坐标选取如下：
[0178]
e
1，2
，e
2，2
，e
3，2
，e
7，2
，e
9，2
，e
5，2
，e
11，2
，e
12k+j，2
；j＝1，2，3，e
12k+7，2
，e
12k+9，2
，e
47，2
，
[0179]
如图7所示，前臂的随动坐标系为a
1，3
x3y3z3。l3为前臂长度。设在t时刻，前臂尾部节点a
1，3
与中间臂轴线上的点q2重合，位于中间臂的第2个插值区间内，区间序号中间
臂头部节点a
4，2
与前臂轴线上的点q3重合，位于前臂的第2个插值区间内，区间序号前臂尾部节点a
1，3
到中间臂尾部节点a
1，2
的距离为l2(t)。前臂的边界条件及主自由度的选取与中间臂类似：
[0180]
e
1，3
，e
2，3
，e
3，3
，e
7，3
，e
9，3
，e
5，3
，e
11，3
，j＝1，2，3，e
12k+7，3
；e
12k+9，3
；e
47，3
，
[0181]
在求解过程中，令t＝0，可得初始状态下的l1(t)|
t＝0
和l2(t)|
t＝0
，进而可得到初始状态下的各插值区间的序号，据此建立约束条件并选择主坐标。
[0182]
在完成主坐标的选择后，可依据静态求解方法求解初始状态，或者依据动态求解方法求解动力学方程，过程如前文所述。举升
‑
回转
‑
伸出复合运动中，各节臂的头部节点的位移仿真结果如图8a
‑
8c所示；各节臂的头部节点的速度仿真结果如图9a
‑
9c所示；忽略了启动(第0～5秒)和制动(第45～50秒)的冲击响应后，各节臂的头部节点在第5秒至第45秒的加速度仿真结果如图10a
‑
10c所示。从仿真结果可以看出，本方法可以有效求解柔性梁系统的举升运动、伸缩运动、回转运动的复合运动。由于举升、伸缩、回转三种基本运动是复合运动的特殊情况，本发明所述的方法也可以应用于对这三种基本运动的仿真求解。
[0183]
应说明的是，以上实施例仅为本发明的较佳实施例，用以说明本发明的技术方案，本发明并不限于列举上述实施例。任何在本说明书的指导下，做出的所有等同替代或明显变形形式，均落在本说明书的实质范围之内，应当受到本发明的保护。