改进的具有混合不确定性多柔体系统动力学预测方法

本发明涉及一种改进的具有混合不确定性多柔体系统动力学预测方法，尤其涉及一种同时具有区间不确定性和随机不确定性参数的多柔体系统动力学响应的预测方法，属于混合不确定性多柔体系统动力学领域。

背景技术：

机械工程领域中最重要的子系统之一就是多体系统。随着高新技术的发展，工程中的技术指标要求越来越高，尤其是高精度、轻质、柔性的部件被广泛应用于空间机械臂、太阳帆板等等。目前大部分研究都集中在确定性参数的柔性多体系统动力学，相当于对模型过分简化，不能正确客观的评价系统真实的响应结果。

由于不可避免的存在固有不确定性和认知不确定性，这些不确定性将会导致多体系统响应也具有不确定性。最常见的三种不确定性有概率不确定性、区间不确定性和模糊不确定性。概率不确定性属于固有不确定的范畴，而区间不确定性和模糊不确定性属于认知不确定性。研究具有混合不确定性的多体系统动力学响应十分重要，尤其是同时具有概率不确定性和区间不确定性的系统动力学更是具有典型的意义。

众所周知，多柔体系统的动力学预测成本是昂贵的，尤其是具有不确定性参数的多柔体系统，需要多次重复调用原系统模型，这使得预测成本愈加昂贵。目前已有各种不确定性的分析方法应用于工程实际问题中。从是否需要对原工程模型系统进行更改的角度出发，不确定性分析方法大体可分为两类：侵入式分析方法和非侵入式分析方法。

侵入式分析方法不需要大量数值仿真，qiu和wang采用参数摄动法得到了时域响应对参数的一阶摄动，虽然可以节省仿真时间，但其实现过程通常十分复杂，不适用于工程中复杂的结构系统。非侵入式分析方法由于其不需要对原模型系统进行更改，相当于“黑箱”模型，因此被广泛应用于工程复杂结构系统的不确定性分析中。wu等采用chebyshev多项式代理模型分析了含区间不确定性参数的系统响应。li等利用随机过程建模描述时变不确定性的系统，并建立kriging代理模型，通过蒙特卡罗仿真计算了系统的时变可靠度。mai和sudret采用混沌多项式展开方法考虑了含随机参数的不确定性系统。

上述方法只适用于解决仅含单一的不确定类型的问题。近年来，研究人员发现在实际工程系统中，不确定性的类型往往是并存的，因此混合不确定性问题的研究拉开了帷幕。west和hosder结合了稀疏抽样和随机展开的方法研究了含有随机和区间混合不确定性的对流换热模型和流体动力学。wu等提出了polynomial-chaos-chebyshev-interval(pcci)方法，该方法采用混沌多项式(polynomialchaos)与切比雪夫多项式(chebyshevpolynomial)相结合的形式构建系统响应的代理模型，并应用于车辆动力学中。

目前混合不确定性问题的研究方法比较有限，而且在实际求解过程中计算量比较大，计算效率较低。

技术实现要素：

针对工程领域中复杂的多体系统，尤其是具有混合不确定性的柔性多体系统，预测其动力学响应的成本是非常昂贵的。本发明公开的改进的具有混合不确定性多柔体系统动力学预测方法要解决的技术问题是：只需较少的样本点数即能够保证在相同精度条件下，预测出具有混合不确定性多柔体系统的输出响应，有效提高具有混合不确定性柔性多体系统动力学响应的预测效率；通过优化随机参数样本点的性能，使得随机样本点具有更好的空间填充性能。本发明应用于机械、航天、车辆、机器人等领域，如柔性机械臂、带附件的航天器，解决所述领域中相关的不确定性预测及相关工程问题。

本发明是通过以下技术方案实现的：

本发明公开的改进的具有混合不确定性多柔体系统动力学预测方法，采用绝对节点坐标公式(ancf)建立确定的多柔体系统的微分-代数方程。将随机不确定性和区间不确定性参数引入多柔体系统模型的方程中，形成混合不确定性微分-代数方程。其次，对同时含随机不确定性和区间不确定性参数的多柔体系统，利用混沌多项式(polynomialchaos)与切比雪夫多项式(chebyshevpolynomial)相结合的形式构建系统响应的代理模型。在选取随机变量样本点时，采用翻转传播算法(flippropagationalgorithm,fpa)生成，fpa方法可快速生成任意尺寸大小的空间填充性能优越的样本。将随机响应面法与广义-alpha算法、自动微分法相结合处理混沌多项式代理模型部分，利用扫描法预测混合不确定性多柔体系统的动力学响应的上下边界。

本发明公开的改进的具有混合不确定性多柔体系统动力学预测方法，包括如下步骤：

步骤1：采用绝对节点坐标公式(ancf)建立确定的多柔体系统的微分-代数方程。

其中m为系统广义质量阵，q为系统广义坐标，f为系统广义弹性力，φ＝0和φq分别为系统约束方程以及对广义坐标的jacobi矩阵，λ为lagrange乘子，q为系统广义外力。

步骤2：将随机不确定性和区间不确定性参数引入多柔体系统模型的方程中，形成混合不确定性微分-代数方程。

其中ξ＝[ξ1,...,ξn]为n个随机参数变量，不失一般性，ξi,i＝1,...,n服从标准正态分布n(0,1)。η＝[η1,...,ηm]为m个区间参数变量，ηj∈[-1,1],j＝1,...,m。其余矩阵和向量的代表意义与步骤1中一致，上标带有“～”的矩阵和向量均为含有不确定性参数的矩阵和向量。

步骤3：对同时含随机不确定性和区间不确定性参数的多柔体系统的输出响应，利用混沌多项式(polynomialchaos)与切比雪夫多项式(chebyshevpolynomial)相结合的形式构建系统响应的代理模型。

其中hi(ξ)和ψj(η)分别为hermite多项式和chebyshev多项式，s和k分别为两种多项式的截断项数。

步骤4：根据双层循环嵌套的形式确定系统参数的样本点。区间变量的样本点位于外层循环，随机变量的样本点位于内层循环。

预测不确定系统响应所需的m组区间参数的样本点由叶等提出的一种快速拉丁超立方试验设计优化方法生成，具有较好的样本空间填充性能和映射性能。由于随机分布中最为经典的就是正态分布，设计新的随机参数采样方法，通过“翻转和剔除”来快速获得任意大小的尺寸且性能较好的随机试验样本，因此将该方法命名为翻转传播算法(flippropagationalgorithm,fpa)。fpa方法一旦生成性能优越的基础样本，无需进行额外的复杂优化运算，“翻转和剔除”过程所需时间忽略不计。预测不确定系统响应所需的n组随机参数的样本点位于内层循环，且随机参数的样本点由上述fpa产生。

利用fpa生成标准正态分布的样本点步骤包括：

步骤4.1：空间样本划分。

将设计空间每一维都一分为二，整个设计空间被划分为等效的数量为2ⁿ的样本模块，其中选择一个模块作为基础样本的选取空间，剩余样本模块参考基础样本按照翻转平移的方法进行填充。假设需要生成一个尺寸为m×n的试验样本，即在n维空间中产生m个样本点，需要构造基础样本的数量为ma×n,ma＝m/a。

步骤4.2：翻转传播。

首先，将基础样本模块均匀分割成maⁿ个空间单元，按连续局部枚方法在maⁿ个空间单元中找出ma个空间单元。

其次，利用基础样本模块与剩余模块的位置关系(n＝2时，位置关系包括左右对称，上下对称，原点对称，依次类推)，将基础样本模块中的ma个空间单元按位置关系进行翻转，对剩余模块中进行填充，总共得到2ⁿma个空间单元。

最后，然后将这2ⁿma个空间单元在每一个维度上平分，此时每个空间单元被分成2ⁿ个小空间单元，每个样本模块(总共有2ⁿ个)从2ⁿ个小空间单元选择一个相对位置作为样本点的生成空间(n＝2时，左下角的样本模块中的空间单元都选择左下角的小空间单元)。每个小空间单元用n维的向量表示为[x1,x2,...xn]，向量中的元素xi∈[1,2,...,m](i＝1,2,...,n)表示小空间单元在当前维度上位置索引。

步骤4.3：剔除多余的样本点。

当步骤4.1中ma＝m/a不是整数时，则重新定义ma＝[m/a]+1，即对ma向上取整。此时按照上述步骤生成样本数量2ⁿma大于所需样本m，因此需要剔除多余的样本点。计算出所有小空间单元坐标到整个空间中心的距离，然后剔除最远距离的空间单元及其所在行和列，并更新剩余小空间单元的坐标。更新所有的坐标以后，再进行距离计算，此时中心也再次更新。依次类推，直至剔除到符合目标数量为止。

步骤4.4：生成样本点坐标。

对每个维度的变量按给定正态分布和取值端点，等概率生成样本点第i(＝1,...,n)维的起始坐标si＝[si,1,si,2,...,si,m]及其区间长度di＝[di,1,di,2,...,di,m]。结合第j(＝1,2,...,m)个小空间格的坐标[x1,j,x2,j,...xn,j]，即可生成第j个样本点的第i维坐标：

yi,j＝si(xi,j)+rand×di(xi,j)(4)

其中，si(xi,j)和di(xi,j)分别表示向量si和di中的第xi,j个元素值，“rand”表示[0,1]之间的随机数。

步骤5：当固定一组外层循环的区间参数样本点η^(w)时，系统退化为仅含随机不确定性参数的情形。利用改进的随机响应面法优化内层循环。

步骤5.1：对原混沌多项式代理模型的n个随机不确定参数分别求其一阶偏导数。

式(5)为固定一组外层循环的区间参数样本点时的仅含随机不确定性参数的系统响应的混沌多项式代理模型。其中q^(w)表示第w组区间样本点下对应的系统的随机输出响应，αi^(w)表示第w组区间样本点下，系统的随机输出响应的混沌多项式代理模型。对式(5)关于各个随机不确定参数分别求一阶偏导数，得到n个关于未知系数αi的关系式，i＝0,...,s-1。第w组区间样本点下，广义输出响应矩阵为

步骤5.2：步骤5.1中的样本响应q可广义-alpha算法求解，一阶偏导数由广义-alpha算法与自动微分法相结合同时求解。

步骤5.3：由步骤5.1和步骤5.2形成共n+1个关于未知系数αi的方程，则仅需要组随机样本点即能够求解出所有的αi，i＝0,...,s-1，但一般情形下，为了保证计算结果的稳定性通常采用两倍的样本点数，故此处采用组随机样本点。

步骤6：利用扫描法估计混合不确定性多柔体系统动力学响应及动力学响应的上下边界，即实现混合不确定性多柔体系统动力学高效率预测。

步骤6.1：对外层循环中的每一组区间样本点都执行步骤5的计算过程。内外两层循环完成之后求得式(1)中的系数矩阵α为

α＝(b(η)^tb(η))^-1b(η)^t((a(ξ)^ta(ξ))^-1a(ξ)^tq)^t(7)其中

当混沌多项式展开阶数p＝2时，由步骤5得到的新的随机转换矩阵a(ξ)为

采用扫描法估计混合不确定性多柔体系统动力学响应。因同时存在随机不确定性和区间不确定性变量，系统的动力学响应结果也同时具有上下界和统计矩的特征。在分析顺序上没有严格要求。

步骤6.2：当先处理区间参数，再进行随机分析，得到的是随机形式的区间解。

步骤6.2.1：先处理区间参数。由步骤6.1估算出系数矩阵α后，采用扫描法估计混合不确定性多柔体系统动力学响应的上界和下界q：

步骤6.2.2：再进行随机分析。步骤6.2.1利用扫描法得到的响应上下界仅包含随机参数：

其中，p′为展开阶数，可根据所需估算精度选取。αi和分别表示αi的下界和上界：

转换矩阵x(ξ)为

其中n′可根据实际估算精度选取。则响应上界的均值(meanofupperbound,mub)、响应下界的均值(meanoflowerbound,mlb)和响应上界的方差(varianceofupperbound,vub)、响应下界的方差(varianceoflowerbound,vlb)分别为

其中<·>表示内积。

根据式(16)(17)估计混合不确定性多柔体系统动力学响应及动力学响应的上下边界，即实现混合不确定性多柔体系统动力学高效率预测。

还包括步骤7：根据步骤1至步骤6实现混合不确定性多柔体系统动力学高效率预测，并将所述分析预测结果应用于不确定性多柔体系统动力学领域，进而解决所述领域中相关的不确定性预测及相关工程问题。

所述混合不确定性多柔体系统动力学领域包括机械、航天、车辆、机器人领域，如柔性机械臂、带附件的航天器多柔体系统动力学预测。

有益效果：

1、本发明公开的改进的具有混合不确定性多柔体系统动力学预测方法，仅需较少的样本点数即可保证在相同精度条件下计算出系统的输出响应。原pcci方法内外双层循环总共需要调用原模型的次数为m×n″＝m×2s。本发明所提的方法仅需要调用原模型的次数为是原pcci方法的倍，能够显著提高具有混合不确定性柔性多体系统动力学响应的预测效率。

2、本发明公开的改进的具有混合不确定性多柔体系统动力学预测方法，利用fpa快速生成任意大小的尺寸且空间填充性能较好的随机试验样本点，通过优化随机参数样本点的性能，使得随机样本点具有更好的空间填充性能，使得预测结果更加有效。

3、本发明公开的改进的具有混合不确定性多柔体系统动力学预测方法，适用于含多个混合不确定性参数的系统，相比目前其他方法，本发明所提方法耗时较少，效率更高，成本更低，更加适用于复杂的工程结构系统。

附图说明：

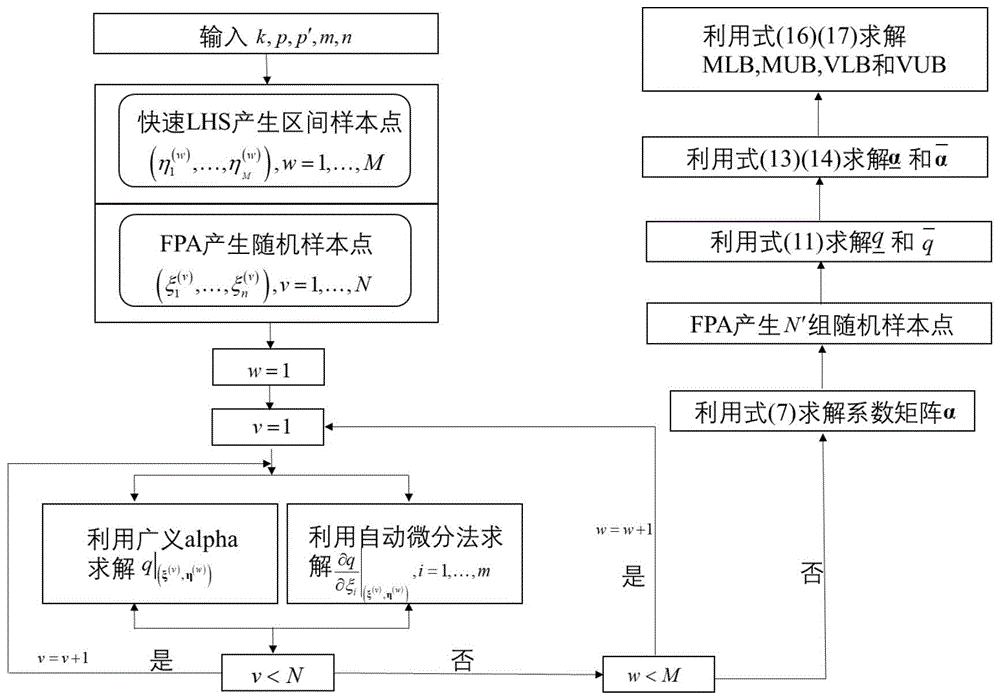
图1为本发明改进的具有混合不确定性多柔体系统动力学预测方法的流程图；

图2为在2维平面随机生成的20个标准正态分布样本点；

图3为根据上述步骤4，采用ftp在2维平面随机生成的20个标准正态分布样本点。

具体实施方式

为了更好的说明本发明的目的和优点，下面结合附图和实例对发明内容做进一步说明。

实施例1：

参照图1，本实施例公开的改进的具有混合不确定性多柔体系统动力学预测方法，具体实现步骤如下：

步骤1：确定多柔体系统的随机和区间不确定性参数的个数，以及随机和区间不确定性所对应的hermite和chebyshev多项式的展开阶数p,k，则相应的内层和外层积分精度分别为2p+1和2k+1。

步骤2：确定双层循环的样本点。根据双层循环嵌套的形式确定系统的样本点。区间变量的样本点采用快速lhs方法产生m组，位于外层循环；随机变量的样本点由fpa产生n组，位于内层循环。图2为20组随机生成的服从正态分布样本点，图3为采用本发明所提方法fpa产生的20组服从正态分布的随机样本点，由图可知本发明所提的采样方法空间填充性能较好，且所需时间忽略不计。

步骤3：当w＝1时，外层循环取第一组区间参数样本点η^(w)，利用改进的随机响应面法优化内层循环。当v＝1时系统广义位移响应q，以及广义位移响应q关于各随机变量的一阶偏导数可利用广义-alpha算法与自动微分法相结合同时求解。

步骤4：当v＝n组随机样本点全部计算完成后重复步骤3，直到w＝m组区间样本点全部计算完成。此时可利用式(7)求解系数矩阵α。

步骤5：再次利用fpa方法产生n′组随机样本点。采用扫描法估计系统动力学响应的上界和下界q。由式(13)和式(14)求解得到系数矩阵上界和下界α。

步骤6：最后利用式(16)和式(17)求解得到系统响应上界的均值、响应下界的均值和响应上界的方差、响应下界的方差。

本实施例公开的方法采用较少的随机样本点数，降低调用原多柔体系统的次数，在相同的预测精度条件下，显著提高预测效率。利用fpa可以快速生成任意大小的尺寸且空间填充性能较好的随机试验样本点，优化了采样性能，使得预测结果更加有效。

根据步骤1至步骤6实现混合不确定性多柔体系统动力学高效率预测，并将所述分析预测结果可应用于任意复杂多体系统领域，如机械、航天、车辆、机器人等，解决所述领域中相关的不确定性预测及相关工程问题。

柔性机械臂、带附件的航天器系统动力学等复杂工程模型，进而解决所述领域中相关的不确定性预测及相关工程问题。

以上所述的具体描述，对发明的目的、技术方案和有益效果进行了进一步详细说明，凡在本发明的精神和原则之内，所做的任何修改、等同替换、改进等，均应包含在本发明的保护范围之内。